数据结构(C语言版) 第9章 排序

1、第9章 内部排序排序：调整记录表中记录次序，使之按关键值有序(增序)。记录表结构：SeqList类内部排序记录集全部在内存中（战术问题）外部排序记录集部分在内存中，排序过程中，需访问外存（战略问题） 稳定性：关键值相同的记录，排序前后的相对次序不变。排序前排序后5 1 4 3 41 3 4 4 5稳定排序1 3 4 4 5不稳定排序 1 插入排序 思路：起源于数据陆续达到的思路，摸牌的行为。1.1 直接插入1.1.1 算法思路与步骤设已存在一个有序子序列；每趟将一个记录按关键值大小插入到有序子序列中。初始化时，有序子序列只有一个记录；n-1趟后，有序子序列有n个记录。初始21254925*81

2、6第1趟21254925*816第2趟21254925*816第3趟212525*49816第4趟8212525*4916第5趟816212525*491.1.2 算法实现/直接插入排序template<class T> void SeqList<T>:InsertSort() int n=m_Data.size(); for(int i=1; i<n; i+) T tmp=m_Datai; for(int j=i-1; j>=0 && m_Dataj>tmp; j-) m_Dataj+1=m_Dataj; / 记录移1位 m_Data

3、j+1=tmp; 1.1.3 性能分析 属于稳定排序。时间复杂度是O(n2)。 KCN：关键值比较次数 RMN：记录移动次数比较移动最好情况记录集有序1次/趟=>KCN=n-12次/趟=>RMN=2(n-1)最坏情况记录集逆序i次/趟=>KCN=n(n-1)/2i+2次/趟=>RMN=(n+4)(n-1)/21.2 希尔排序发明人：D.L.Shell，发明于1959年。1.2.1 算法思路与步骤直接插入排序的缺点：每个记录被一步一步地挪到目标位置。将记录较快地挪到目标位置的方法：加大步长。仅仅加大步长的值，可行吗？缩小增量法：最后一次的步长一定为1。 希尔排序：将记录序

4、列按某个步长分成若干子序列；分别对各子序列排序。步长的取值方法之一：n/2,n/4,8,4,2,1。初始561748329第1趟步长=4461258379第2趟步长=2123647589第3趟步长=11234567891.2.2 算法实现template<class T> void SeqList<T>:ShellSort() int n=m_Data.size(); for(int step=n/2; step>0; step=step/2) for(int i=step; i<n; i+) T tmp=m_Datai; for(int j=i-step;

5、 j>=0 && m_Dataj>tmp; j=j-step) m_Dataj+step = m_Dataj; / 记录移step位 m_Dataj+step=tmp; 1.2.3性能分析 属于不稳定排序。(各子序列彼此独立的交换) 时间复杂度：O(n1.5)O(n1.3)。第9章 内部排序3 选择排序思路：“比较”比“赋值”速度快得多3.1 直接选择排序3.1.1 算法思路与步骤 每趟：在剩余序列中找到最小值，将之交换到目标位置。 n-1趟选出n-1个极值，置于相应目标位置。初始561748329第1趟165748329第2趟1257483693.1.2 算法实现

6、template<class T> void SeqList<T>:SelectSort() int n=m_Data.size(); for(int i=0; i<n-1; i+) int min_i=i; for(int j=i+1; j<n; j+) if(m_Dataj<m_Datamin_i) min_i=j; if(i!=min_i) T tmp=m_Datai; m_Datai=m_Datamin_i; m_Datamin_i=tmp; 3.1.3 性能分析 时间复杂度：O(n2) 空间复杂度：O(1) 稳定性：不稳定。示例：排序前3 4

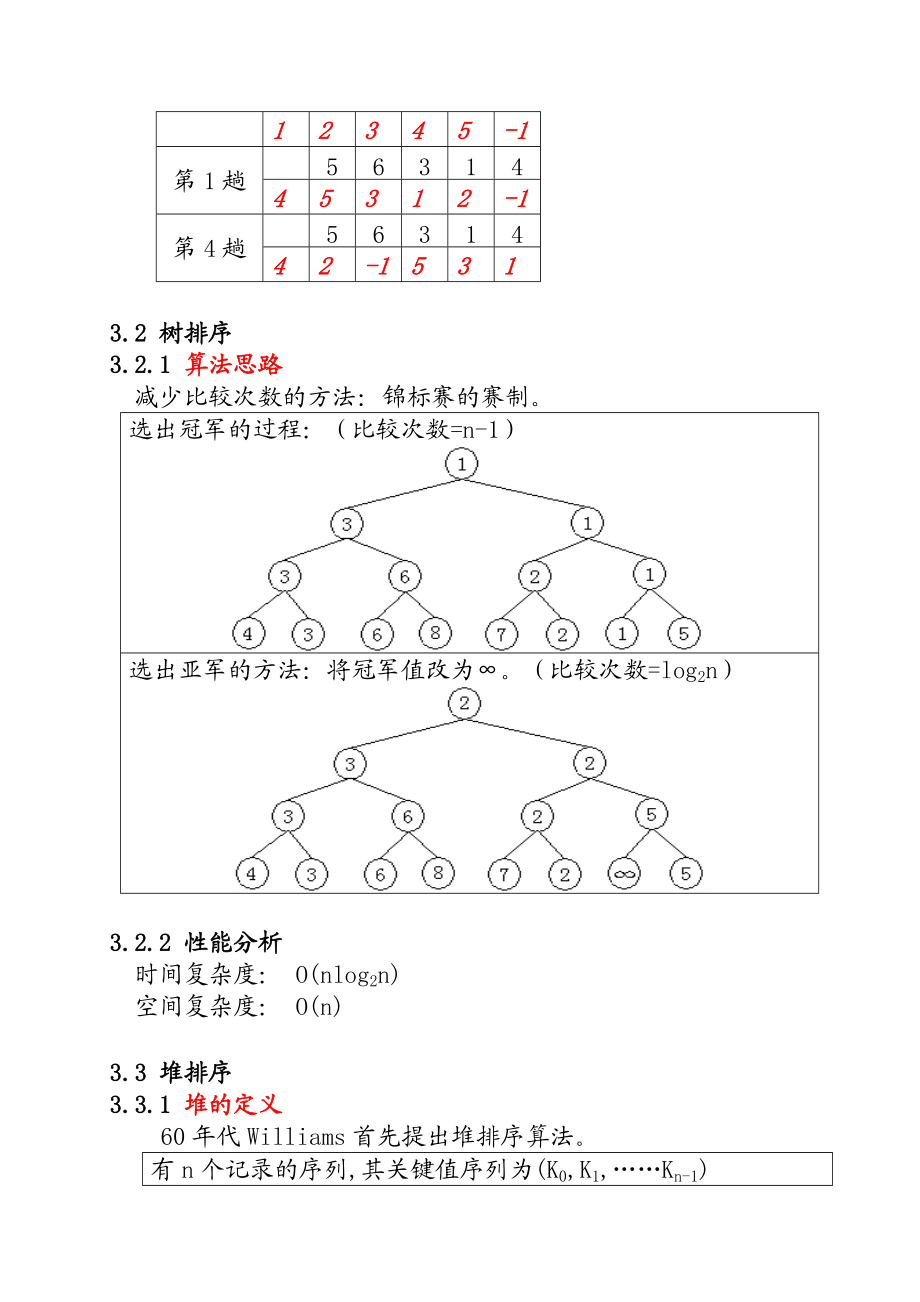
7、 5 3 1 一趟后1 4 5 3 33.1.4 扩展思考 减少移动记录的方法：采用静态链表结构。 示例：普通的直接选择排序 初始56314第1趟16354 例：基于静态链表的直接选择排序 下标012345初始5631412345-1第1趟5631445312-1第4趟5631442-15313.2 树排序3.2.1 算法思路减少比较次数的方法：锦标赛的赛制。选出冠军的过程：（比较次数=n-1）选出亚军的方法：将冠军值改为。（比较次数=log2n）3.2.2 性能分析时间复杂度： O(nlog2n)空间复杂度： O(n)3.3 堆排序3.3.1 堆的定义60年代Williams首先提出堆排序算

8、法。 有n个记录的序列,其关键值序列为(K0,K1,Kn-1) 若2i+1<n，则有Ki<=K2i+1 若2i+2<n，则有Ki<=K2i+2本质：将序列当作完全二叉树的顺序存储形式。 每个分支结点的关键值 <= 其左右孩子结点的关键值称为小根堆。3.3.2 建堆方法 建堆是一个依次调整结点的过程。 从简单的事做起：从最后一个分支结点开始调整！初始情形调整结点(i=3)3,4,5,1,6,8,2,73,4,5,1,6,8,2,7调整结点(i=2)调整结点(i=1)3,4,2,1,6,8,5,73,1,2,4,6,8,5,7调整结点(i=0)1,3,2,4,6,8,

9、5,73.3.3 堆排序方法 堆排序是n-1次交换、调整结点的过程。 第1次交换第1次调整7,3,2,4,6,8,5,(1)2,3,5,4,6,8,7,(1)第2次交换第2次调整7,3,5,4,6,8,(2,1)3,4,5,7,6,8,(2,1)3.3.4 堆排序的实现template<class T> void SeqList<T>:HeapSort() int n=m_Data.size(); for(int i=n/2-1; i>=0; i-) HeapShift(i,n-1); for(i=n-1; i>0; i-) T tmp=m_Data0; m

10、_Data0=m_Datai; m_Datai=tmp; HeapShift(0,i-1); / 调整范围：m_Datarootm_Databottomtemplate<class T> void SeqList<T>:HeapShift(int root,int bottom) T tmp=m_Dataroot; int ch_i=2*root+1; while(ch_i<=bottom) if(ch_i+1<=bottom && m_Datach_i>m_Datach_i+1) ch_i+; / ch_i是左右孩子中较小者的下标 if(m_Datach_i >= tmp) break; m_Dataroot = m_Datach_i; root=ch_i; ch_i=2*root+1; m_Dataroot=tmp;3.3.5 性能分析时间复杂度： O(nlog2n) 其中：建堆O(n)，每次调整O(log2n)空间复杂度： O(