天津市和平区2017年中考数学专题练习平行四边形50题

1、平行四边形50题一、选择题：1.下列语句正确的是（）A.对角线互相垂直的四边形是菱形B.有两边及一角对应相等的两个三角形全等C.矩形的对角线相等D.平行四边形是轴对称图形2 .平行四边形 ABCDW等边 AEF如图放置，如果/ B=45 ,则/ BAE的大小是（）B.70A.75C.65 D.603 .已知四边形 ABCD平行四边形，再从 AB=BC/ ABC=90 ;AC=BDAd BD.四个条件中，选两个作为补充条件后，使得四边形 ABC皿正方形，现有下列四种选法，其中错误的是（）A.选 B. 选 C. 选D. 选4 .在 ABC中，点D, E, F分别在BC AB, CA上，且DE/ C

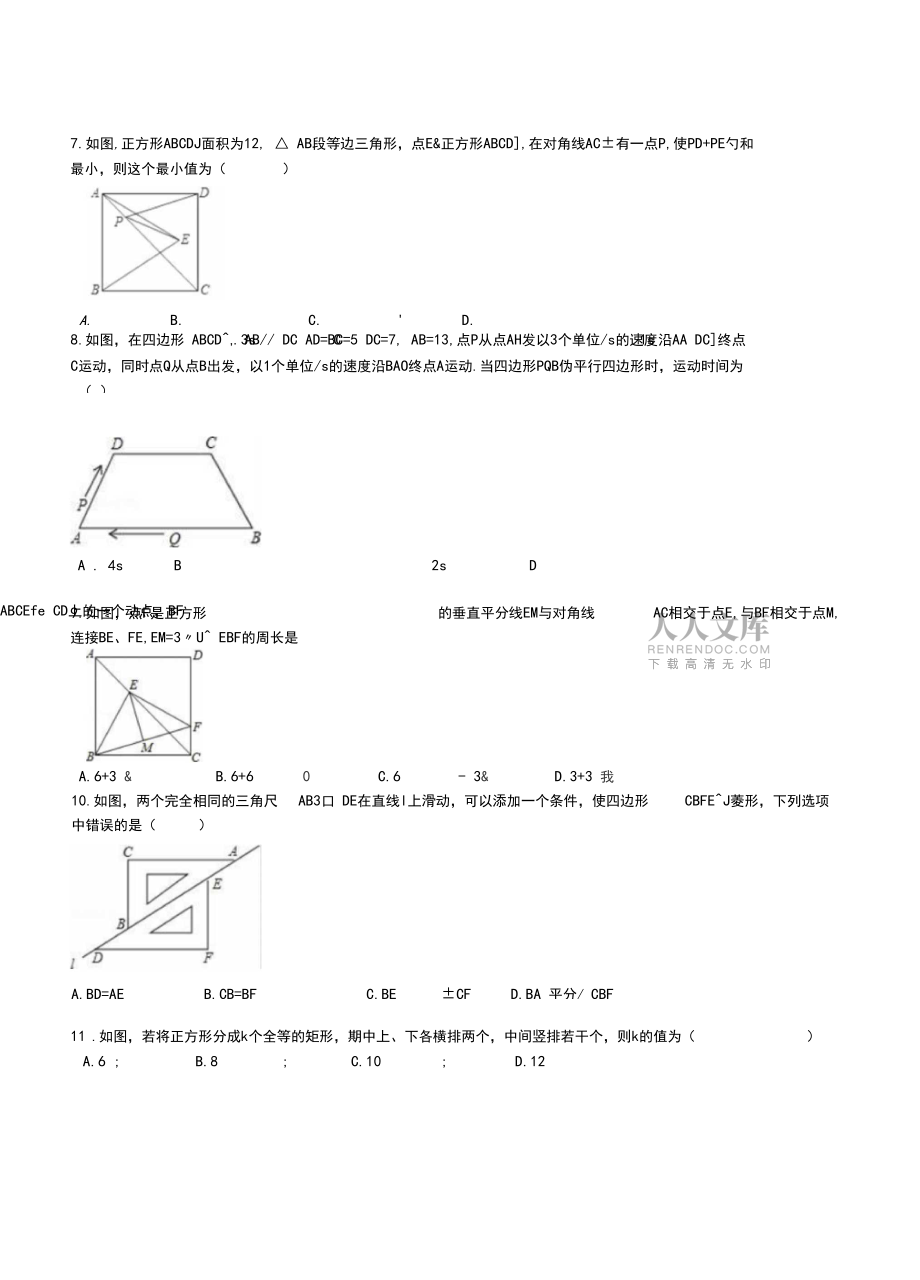
2、A, DF/ BA,连接EF,则下列三种说法:如果EF=AD那么四边形AEDF是矩形如果EF AD,那么四边形 AEDF菱形如果AD BC且AB=AC那么四边形AEDF是正方形其中正确的有（）A.3 个 B.2 个 C.1 个 D.0 个5 .如图，将正方形OABC：在平面直角坐标系中，0是原点，若点A的坐标为（1, 5,则点C坐标为（）A.（ 31）B.（-1,4）C.（-31） D.（-5-1）6 .如图，以A、B为顶点作位置不同的正方形，一共可以作 （）AB1A.1 个B.2个C.3个D.4个7.如图,正方形ABCDJ面积为12, AB段等边三角形，点E&正方形ABCD,在对角线AC有一

3、点P,使PD+PE勺和 最小，则这个最小值为（）A.B.C.D.8.如图，在四边形 ABCD, AB/ DC AD=BC=5 DC=7, AB=13,点P从点AH发以3个单位/s的速度沿AA DC终点C运动，同时点Q从点B出发，以1个单位/s的速度沿BAO终点A运动.当四边形PQB伪平行四边形时，运动时间为（ ）CA . 4sB.3s2sD.1sABCEfe CD上的一个动点，BF的垂直平分线EM与对角线AC相交于点E,与BF相交于点M,9.如图，点F是正方形连接BE、FE,EM=3U EBF的周长是A.6+3 &B.6+60C.6- 3&D.3+3 我10.如图，两个完全相同的三角尺AB3口

4、 DE在直线l上滑动，可以添加一个条件，使四边形CBFEJ菱形，下列选项中错误的是（）A.BD=AEB.CB=BFC.BECFD.BA 平分/ CBF11 .如图，若将正方形分成k个全等的矩形，期中上、下各横排两个，中间竖排若干个，则k的值为（）A.6 ;B.8;C.10;D.1212 .在一个边长不超过 8厘米的大正方形 ABCM,如图所示，放入3张面积都是20平方厘米的小正方形纸片 BEFGOPNC IQKJ,已知3张小正方形纸片盖住的总面积为44平方厘米，那么大正方形ABCDF口小正方形BEFG勺边长C.10: 7D.8DCA.1B.2C.3D.4ABCM对角线，AE，BC于点E,交BD

5、于点F,且E为BC的中点,则cos / BFE的值是（14.如图，BD是菱形CA.B.C.D.13 .如图，在周长为12的菱形ABC邛,AE=1,AF=2,若P为对角线BD上一动点，则EP+FP的最小值为（ AE15 .如图，正方形AEFG勺边AEM置在正方形ABCD勺对角线AC, EF与C戊于点M,得四边形AEMD且两正方形的边长均为2,则两正方形重合部分（阴影部分）的面积为（D，& + 116.如图，正方形ABCD CEFG勺边长分别为A.与mr n的大小都有关C.只与m的大小有关B.D.m n,那么？AEG的面积的值与m n的大小都无关 只与n的大小有关BC E17 .如图，四边形ABC

6、D,ADW BC不平行,AB=CD.AC,BD为四边形 ABCD勺对角线，E,F,G,H 分别是BD,BC,AC,AD的中 点.下列结论：EGL FH;四边形EFGH矩形；HF平分/ EHGEG= （BC- AD）;四边形EFGH菱形.其中正确的个数是（）B F CA.1个B.2个C.3 个D.4个18 .如图，将一张等边三角形纸片沿中位线剪成4个小三角形，称为第一次操作；然后，将其中的一个三角形按同样方式再剪成 4个小三角形，共得到7个小三角形，称为第二次操作；再将其中一个三角形按同样方式再剪成 4个小三角形，共得到 10个小三角形，称为第三次操作；根据以上操作，若要得到100个小三角形，则

7、需要操作的次数是（）A. 25B . 33 C . 34D .5019 .如图，正方形ABCDJ边长为6,点E、F分别在AB,AD上,若CE&行，且/ ECF=45，则CFK为（）A.B.三,；C.D./20 .如图，在正方形 ABCD43,AC为对角线,E为AB上一点，过点E作EF/ AD,与AG DC分别交于点 G,F,H为CG的 中点，连接DE, EH DH FH.下列结论：EG=DF/ AEH吆 ADH=180 ;A EHF DHCAE 2若一=,则3sED=13Sa DHC,其中结论正确的有（）A.1 个 B.2 个 C.3 个 D.4个二、填空题：21 .如图，将矩形纸片ABC断B

8、E DFf叠后，顶点A、C恰好都落在对角线 BM中点O处.若BD=6cm,则四边形BEDF 的周长是 cm.DB22 .正方形的判定：的平行四边形是正方形；(2)的矩形是正方形；(3) 的菱形是正方形；23 .如图，四边形ABCD1一张矩形纸片，AD=2AB若沿过点D的折痕D曰各At翻折，使点A落在BCk的Ai处，则/ EAB=。24 .如图，在？ABCM ,对角线 AC BD相交于点 O.如果AC=8,BD=14,AB=x,那么x取值范围是 25 .如图，在矩形ABC中,对角线AG BDW交于点。，若DF!AC,/ADF: / FDC=3:2, 贝U/ BDF=26 .如图,矩形ABCD的长

9、为10,宽为6,点E、F将AC三等分,则4 BEF的面积是 DCAB27 .如图，四边形ABCD1正方形，延长 AB UE,使AE=AC则/ BCE勺度数是 度.DC3 BE28.如图，矩形ABC沿着直线B斯叠，使点湍在C处，BC交AD点E, AD=8, AB=4,则DE勺长为29.如图，一张宽为6cm勺矩形纸片，按图示加以折叠，使得角顶点落在 AB&上,则折痕DF= cm.30.如图，正方形ABCDJ四个顶点A B C、D正好分别在四条平行线11、13、 线间的距离都是 2cm,则正方形ABCDJ面积为cm 2.l 4、l 2上，若从上到下每两条平行31.如图，折叠矩形纸片 ABCD先折出折

10、痕BD,再折叠使ADa与对角线BDt合，彳#折痕DG若AB=4, BC=3则AG 的长是.32.如图，在矩形AOB中,点A的坐标是（-2, 1）,点C勺纵坐标是4,则B、C两点的坐标分别是33.一个四边形四条边顺次是a、b、c、d,且a2+b2+c2+d2=2ac+2bd ,则这个四边形是 34 .如图，面积为1的正方形ABC邛，M N分别为AD BC的中点，将C点折至MN,落在P点的位置，折痕35 .如图，在Rt ABC，/ACB= 90 ,以Aa边正方形面积为 12,中线C*度为2,则BC度为36 .如图，矩形 ABC中,AB=6,AD=8,P 是BC的点，PE，BDf E,PF，ACf

11、F,贝U PF+PE=B37 .如图，在矩形ABC中，点E是边CD勺中点，将 ADE&AEW叠后彳#到4 AFE且点F在矩形ABCD部.将A%长交边B计点G.若BG=kCG则AD:AB= D用含k的代数式表示）.38 .如图,/ MON=90 ,矩形ABCD勺顶点A、的别在边OM ONE ,AB=4,BC=1.当点队边ONE运动时，点AB之在边 OM 上运动，运动过程中矩形ABCDJ形状保持不变，则点 DU点O勺最大距离是.39 .如图，在正方形 ABC冲,E、F分别是边BC CDh的点，/ EAF=45 , ECF勺周长为4,则正方形ABCD1边长 为.40 .如图，在矩形ABC中,AD=5

12、,AB=8,点E为DC&上的一个动点，把AADE&A斯叠，当点D的对应点刚好 的在矩形 ABCDJ对称轴上时，则DE勺长为.三、解答题：41 .如图，已知在 DABCtD ,E、F是对角线AC的两点，且AE=CF 求证：四边形BEDF1平行四边形.（图1）1,线段AC的两个端点42 .图1、图2是两张形状和大小完全相同的方格纸，方格纸中每个小正方形的边长均为 均在小正方形的顶点上.（1）如图1,点P在小正方形的顶点上，在图 1中作出点P关于直线AC的对称点Q,连接AQ QC CP PA,并 直接写出四边形 AQCP勺周长；个以线段 AC为对角线、面积为 6的矩形ABCD且点B和点D均在小正方形

13、的顶点上.43 .如图，在平行四边形 ABC中,AB=6,AD=9, / BAD勺平分线交BC于E,交DC勺延长线于F,BGi A盯G,BG=4近.求：（1） AE勺长；（2） EFM面积；44 .如图，已知在菱形ABCD,F为边BC勺中点，DF与对角线AC于M,过MMELCDFE,/1 = /2.（1）若 CE=1,求 BC勺长；（2）求证：AM=DF+ME45 .准备一张矩形纸片，按如图操作：将ABE沿BE翻折，使点A落在对角线BD上的M点，将 CDF沿DF翻折,使点C落在对角线BD上的N点.(1)求证：四边形 BFDE是平行四边形；(2)若四边形BFD既菱形，AB=2,求菱形BFDE的面

14、积.46 .如图，已知矩形ABCDJ边长AB=3cm,BC=6cm某一时亥I,动点 MAA点出发沿AB方向以1cm/s的速度向B点匀速运 动；同时，动点NMD自出发沿DAT向以2cm/s的速度向A直匀速运动，问：(1)经过多少时间， AMNJ面积等于矩形 ABC面积的九分之一？(2)是否存在时刻t,使以A,M,N为顶点的三角形与 AC。目似？若存在，求t的值；若不存在，请说明理由.Cr-iB47 . (1)如图1,在正方形ABC冲，点E, F分别在边BC, CDk, AE, B咬于点O, / AOF=90 .求证：BF=AE(2)如图2,正方形ABCDL长为12,将正方形沿MNf叠，使点 够在

15、D地上的点E处，且DE=5求折痕MN勺长.(3)已知点E, H, F, g别在矩形ABCDJ边AB, BC CD DA, EF, G出于点O, / FOH=90 , EF=4.直接写出 下列两题的答案：如图3,矩形ABC由2个全等的正方形组成，则 GH=;如图4,矩形ABC由n个全等的正方形组成，则 GH=.(用n的代数式表示)邸S448 .如图1,在 OABK / OAB=9趴 / AOB=30, OB=8以O斯一边，在 OAB7卜作等边三角形 OBC 皿OB勺中点，连接A9延长交OCF E.(1)求点B的坐标；(2)求证：四边形ABCE1平行四边形； 如图2,将图1中的四边形ABC所叠，使

16、点Cf点AM合，折痕为FG求OG勺长.49 .如图，在矩形纸片ABC中，AB=4, AD=12,将矩形纸片折叠， 使点湍在AM上的点 泄，折痕为PE此时PD=3 (1)求MP勺值；(2)在AE&上有一个动点F,且不与点A, B重合.当AF等于多少时， ME的周长最小？(3)若点G, Q是ABa上的两个动点，且不与点A, B重合，GQ=2当四边形MEQG周长最小时，求最小周长值.(计 算结果保留根号)50 .在平行四边形 ABC中，E是ADh一点，AE=AB过点E作直线EF,在EF上取一点G,使彳导/ EGBh EAB,连接AG(1)如图，当 EFf ABf交时，若/ EAB=60 ,求证：EG

17、=AG+BG(2)如图，当EFf CD交时，且/ EAB=900 ,请你写出线段EG AG BZ间的数量关系，并证明你的结论.DA口G参考答案1 .C2.A3.B4.B5.C6.C7.B8.B9.B10.A11.B12.D .13.C14.C15.A16.D17.C18.B .19.A20 .D.21 .答案为:k小(2)有一组邻边相等.(3)有一个角是直角.22 .答案为：(1)有一组邻边相等，并且有一个角是直角;23 .答案为：60 .24 .答案为：3VXV11.25 .答案为：18 ;26 .答案为：10.27 .答案为22.5 .28 .答案为：5;29 .答案为：8;30 .答案为

18、：20;31 .答案为：1.532 .答案为：(1.5 , 3)、(- 0.5 , 4).33 .答案为:平行四边形34 .答案为：1/3;35 .答案为：236 .答案为：4.8 .37 .答案为：38 .答案为:S * 工39 .答案为:2 .40 .答案为：2.5或上黄. 一41 .证明：连结BD与AC交于点O,如图所示：四边形 ABC皿平行四边形，AO=CO BO=DO 又 AE=CFAO- AE=CO- CF,EO=FO四边形BEDF为平行四边形.月 J42.解：(1)如图1所示：四边形 AQCFP为所求，它的周长为： 4xV10=4V10；（图1）43.解：二.在？ABCDK.Z

19、BAF=Z DAF,AB=CD=6 AD=BC=9 / BAD的平分线交 BC于点 E, AB/ DF, AD/ BC / BAF=/ F=Z DAF, / BAE=/ AEBAB=BE=6 AD=DF=9. ADF是等腰三角形， ABE是等腰三角形，在4ABG中，BGLAE, AB=6, BG=4J2 ,AG=jAB2 - BG =2, AE=2AG=4.ABE的面积等于8/2，又CES BEA相似比为1 ： 2,CEF的面积为2& ,.44. (1)解：二四边形 ABC虚菱形，AB/ CD/ 1 = /ACD /1 = /2, ACD= 2, MC=MD / MEL CD CD=2CE C

20、E=1, CD=2 .1. BC=CD=2(2)证明：如图，: F 为边 BC的中点，BF=CF=BC, . CF=CE 在菱形 ABCM, AC平分/ BCD 1 / ACB4 ACD,CKF在CEMF 口 4CFM 中， , .CE阵 CFM (SAS ,ClXJtME=MF 延长 AB交 DF的延长线于点 G, AB/ CD, . / G=/ 2,ZG=Z2 /1 = /2,1=/G, . . AM=MG在 CDF和ABGF中，. 一EFC二一仃W 计师扇相舌 i,WKF. .CD障 BGF (AAS),，GF=DF 由图形可知， GM=GF+M F，AM=DF+M EC D45.解答】

21、(1)证明四边形ABCD是矩形一.,NA=NC=90* + ABK口，ABCD, AZABI=ZCDB, AZEBD=O. 5ZABI=ZFTBf AEB/DF,VEDft BF,四边形BFDE为平行四边彤.(2)解四边形 BFDE 为菱形 jZEBP=ZraP=ZABEf 四边形 出力是矩形小氏，/ABC二90，二/ABE:90,VZA=90* , AB2 二陋=云BFsBE-2AE=-y, 故菱形丽E的面积为；孥乂空挛，3346.解：(1)没经过k杪后，的面爬等于矩招面积的1 ,9则有：一(6 - 21)*二一乂3乂6 ,即-3工+2匹0 ,解方程，得再=1啊=2. 29经检凿，可知七=1

22、%= 2符合题意，所以经过1秒或2秒后，的面积等于矩升面枳的92假设经过工杼寸，以A M. N为璘点的三角形与乙纥。相似, 由亚兆松co,可得/cn4=/MW=9(r1AM DAM DCH U，一上好 0C .因此有= 式AN DA峰.第,再上二年.* 二轻蝇以二2或上二2都为合麴意，械动点M,“降寸出发后， 25经过枭或与视明以4 北 川为顶点的三招与A/8相以 2547. (1)证明：如图，二四边形 ABCM正方形，AB=BC / ABC玄 BCD=90 , . . / EAB吆 AEB=90 . / EOBh AOF=90 , / FBC47 AEB=90 ,. / EAB土 FBQ在A

23、BE和 ABCF中，/ EAB4 FBC,AB=BC/ABCh C, . AB段 BCF (ASA), . AE=BF(2)解：如图2,连接AE,过点N作NHL AD于H,由折叠的性质得， AE! NM / DAE4Z AMN=90 , / MNH+ AMN=90 ,. / DAEh MNH在 ADEn NHMK / DAE= MNH,AD=NH, MHN= D,. .AD段NHM(ASA), . AE=MN-DE=5 .由勾股定理得， AE=13, . MN=13(3)解：如图 3、4,过点F作FMLAB于M,过点 G作GNL BC于N, ./FOH=90 ,MFE=Z NAH 又EMF=Z

24、 HNG=90 ,EFMh HNG . GH:EF=GN:FM 图 3, GN=2FM GH=2EF=2 4=8,图 4, GN=nFM GH=nEF=4n 故答案为：8, 4n.48.卸411)在OAB 中，0AB=90 . 一且+ 0B=8, .OA-43 , ABE.二点B的坐标为( A 4) .*/0AB=9O”，铀，XBE匚 又;BC是等边三角形，二OC=0际B.又：D是0E的卬点，即仙是RtiOAB斜边上的甲线，AAIWDj ,/03/AOB30*, /.OEM.JEC=0C-CE=4.，AB=EC,二四边形ABCE是平行四边形.小题3：设8=小则由折叁对称的生&,饵GA=8=8-x在KtAOAG卬，由与股定理,浮GA工 0A；-OG、即is-工rJT一炉,醉得，尸i*二oc的长为l49.解：(1)二.四边形 ABC的矩形，CD=AB=4 Z D=90 ,矩形ABC所叠，使点C落在AD边上的点M处，折痕为PE,. PD=PH=3 CD=MH=,4 / H=Z D=90 ,. MP=5(2)如图1,作点M关于AB的对称点 M ,连接M E交AB于点F,则点F即为所求