二节微积学基本定理-资料 ppt课件

1、第二节第二节 微积学根本定理微积学根本定理一、变上限积分与对积分一、变上限积分与对积分上限变量求导数上限变量求导数二、微积分根本定理二、微积分根本定理 假设物体运动的速度函数为v=v(t),那么在时间区间a,b内物体的走过的路程s可以用定积分表示为.d)(battvs另一方面,假设知该变速直线运动的路程函数为s=s(t),那么在时间区间a,b内物体的位移为s(b)s(a), 所以又有 ).()(d)(asbsttvba由于 ,即s(t)是v(t)的原函数,这就是说,定积分 等于被积函数v(t)的原函数s(t)在区间a,b上的增量s(b)s(a).)()(tvtsbattvd)(一、变上限积分与

2、对积分上限变量求导数 设函数f(x)在区间a,b上延续,那么对于恣意的x( ),积分 存在,且对于给定的x( ),就有一个积分值与之对应,所以上限为变量的积分 是上限x的函数.bxaxaxxfd)(bxaxaxxfd)(留意：积分上限x与被积表达式f(x)dx中的积分变量x是两个不同的概念,在求积时(或说积分过程中)上限x是固定不变的,而积分变量x是在下限与上限之间变化的,根据定积分与积分变量记号无关,用字母t表示积分变量,于是变上限记号为(x)因此常记为定理5.3 假设函数f(x)在区间a,b上延续,那么变上限的积分所确定的函数).( )(d)(dd)( bxaxfttfxxxa( )( )

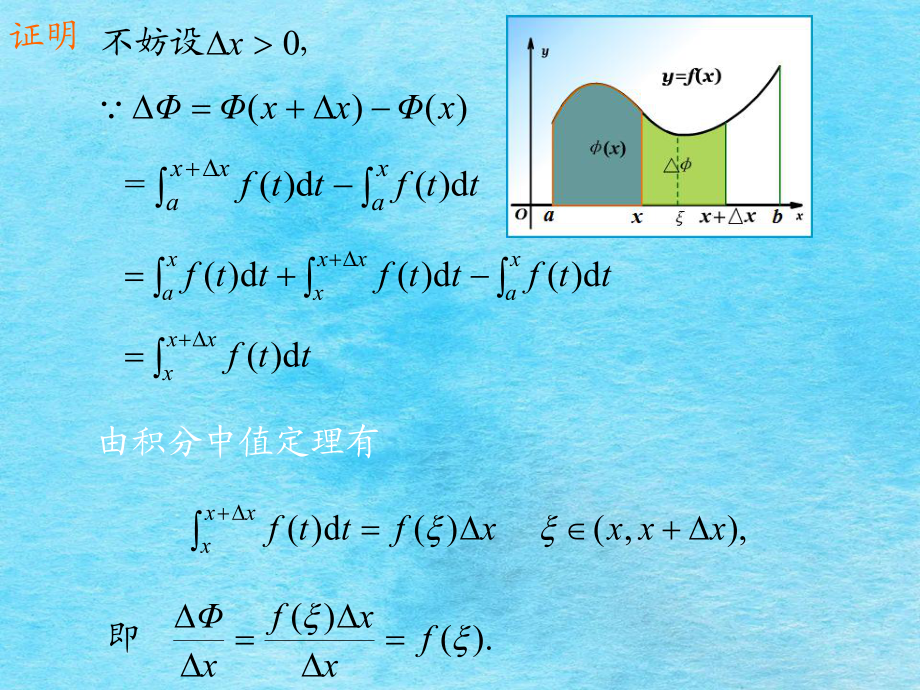
3、d .xaxf tt( )( )d ().xa xf ttaxb在a,b上可导,且xaxxattfttfd)(d)(=xxxxaxxxxattfttfttfttfd)(d)(d)(d)()() (0 xxxx，不妨设证明),( )(d)(xxxxfttfxxx由积分中值定理有).()( fxxfx即数的连续性，有根据导数的定义以及函，从而时，有当 0 xxxxx结论：变上限积分所确定的函数 对积分上限x的导数等于被积函数f(t)在积分上限x处的值f(x).xattfd)(，)()(limlim)( 0 xffxxxx).(d)(dd)( xfttfxxxa即.,)(d)()( ,)( 上的一个

4、原函数在是上连续，则在区间如果函数baxfttfxbaxfxa定理5.4(原函数存在定理) 原函数存在定理一方面阐明延续函数必有原函数,另一方面又提示了延续函数定积分(这里是指变上限定积分)与不定积分的关系,并由此可以得到利用原函数计算定积分的公式(称为微积分根本定理).0 ( )( ) ( )( )d( )+.xaF x xCxf ttF xC定理5.5(微积学根本定理) 设函数f(x)在区间上延续,且F(x)是f(x)在a,b上的任一原函数，)()(d)(aFbFxxfba二、微积分根本定理证明的一个原函数，也是而的一个原函数，是)(d)()()()(xfttfxxfxFxa( )d( )

5、( )( ).bbaaf x xF xF bF a或记作 上式称为牛顿-莱布尼茨公式,也称为微积分根本定理.，即)()(d)( aFbFxxfba那么 即有0( )CF a ( )d( )( ).xaf ttF xF a令x=b得( )d( )( ),baf ttF bF a00=( )d( )+aaf ttF xC令x=a,得 牛顿莱布尼茨公式提供了计算定积分的简便的根本方法,即求定积分的值,只需求出被积函数 f(x)的一个原函数F(x),然后计算原函数在区间a,b上的增量F(b)F(a)即可.该公式把计算定积分归结为求原函数的问题,提示了定积分与不定积分之间的内在联络.d102xx例1 求的一个原函数，是被积函数因为xx233 解.31333d 0133103102xxx莱布尼茨公式，有根据牛顿例2 求.d11112xx11112arctand11xxx莱布尼茨公式，有根据牛顿的一个原函数，是被积函数因为 11arctan 2xx 解.2 )4(4) 1arctan(1arctan21dln(1)d dxtt .x例3 求221d(1)d(1)dxlnttlnx .x 解 根据定理6.3有例4 求.darctanlim200 xxxtt必达法则，有型的极限问题，利用洛这属于00 xt