工程力学禹奇才答案

1、XBYBNAQPCAB3-2解：以整体为研究对象 Y =0， YBQP0MA=0， XB cPaQb 0MB=0， NAc PaQb0 YB QP XB RANBFABM NA 3-4（a）解：以整体为研究对象MA=0， NB ·2aMF·3a 0MB=0， RA·2aMF·a0 NB RARANBP1ABP23-7（a）解：以整体为研究对象MA=0， NB ×0.6P1×0.2P2×0.40MB=0， RA×0.6P1×0.4P2×0.20 NB5kN RA4kNRANBP2AB (b) 解：

2、以整体为研究对象MA=0， NB ×0.4P2×0.60MB=0， RA×0.4P2×0.20 NB9kNRAABMP3MAC RA3kN(c) 解：以整体为研究对象MA=0， MAMP3 ×0.50Y =0， RAP30 MAMP3 ×0.50.21×0.50.3kN RAP31kN3-9解：以整体为研究对象首先考虑满载时，起重机不向右翻倒的最小w3为：限制条件：NA0B10mx3m1.5mAW1W3W2NANBMB=0，W3（x3）W1×1.5W2×10=0 空载时，W1=0，限制条件为：NB0MA=

3、0，W3·xW1×4.5=0 解方程 得 x 6.75m W3333.33kN AXOYOOSP3-11解：以AO、DCB为研究对象CBDNYCXCS 对AOMO=0， S·cos45°×0.3P×1.5=0 对DCBMC=0， S·cos45°×1.2S·sin45°×0.2N×0.2=0 S P× 0.343kN343NQXBYBRBCE3-13解：解：以BCE、AOB为研究对象 对BCEXBYBXOYOWBAO Y0, YBQ0 对AOBM0, YB

4、·a Wx0 x3-15解：以整体、AC为研究对象ASABqCRAXCYCDqCBRARBA 对整体(利用对称性)可知 RARB q×4.55×4.522.5kN 对ACMD 0， XC ×1.5q ×4.5×2.25RA×4.50MC 0， SAB×1.5q ×4.5×2.25RA×4.50Y 0， RAYCq ×4.50解方程 XC 33.75kN YC q×4.5RA5×4.522.50 SAB33.75kNXBYBNCBC3-19解：以AC、BC为

5、研究对象XAYANCWAC 对ACMA 0， Wbcos WasinNC·2lcos0 NC(Wbcos Wasin)/ 2lcos对BCMB 0， MNClcos0 MNClcosW (bcos asin)/ 2CBXBYBXCYCqCBAXAYAXBYBq 3-22解：以整体、BC为研究对象对整体MA 0，q×8×4YB×8XB×40MB 0，XA×4YA×8q×8×40X 0， XBXA0对BCMC 0，q×2×4YB×4XB×40MB 0，XC×4

6、YC×4q×2×40X 0， XBXC0联立求解YBq ×1550kN XB2qYB2×155020 kN XBXC XA 20 kNRARB4kN4kNABCDE YA（q×8×4XA ×4）/870 kN YC （q×4×2XC ×4）/410 kNSDCDSDESAD4kNSACSADRAA3-25(a)解：以整体研究对象 利用对称性可知 ： RARB 4kN, SADSEB , SDCSEC , SACSBC以节点A、D研究对象对节点A X=0， SAC SAD cos60&#

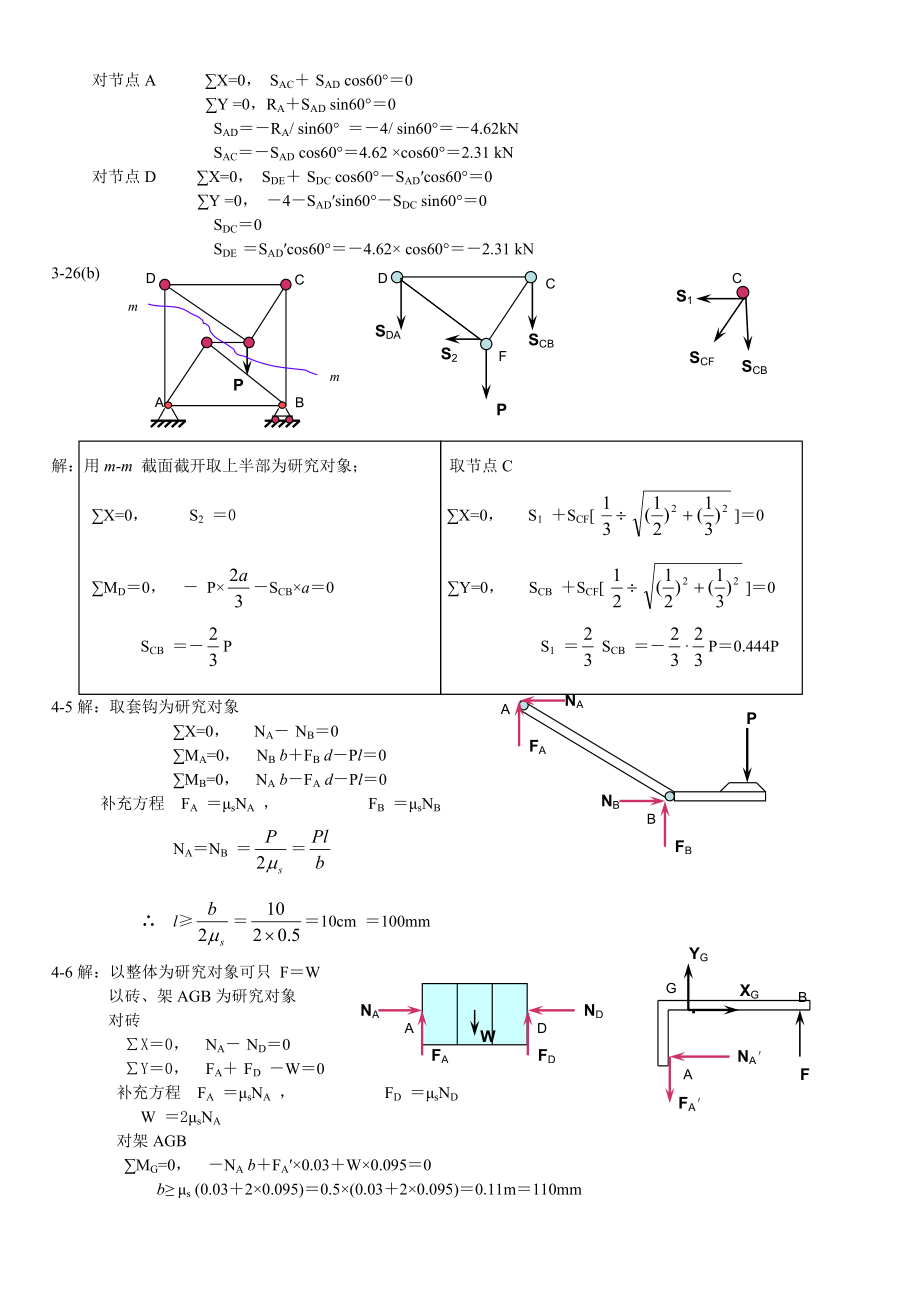
7、176;0Y =0，RASAD sin60°0 SADRA/ sin60° 4/ sin60°4.62kN SACSAD cos60°4.62 ×cos60°2.31 kN 对节点D X=0， SDE SDC cos60°SADcos60°0Y =0， 4SADsin60°SDC sin60°0 SDC0 SDE SADcos60°4.62× cos60°2.31 kN CS1SCFSCBSCBCDFSDAS2PPCDABmm3-26(b) 解：用m-m 截面截开取

8、上半部为研究对象； 取节点C X=0， S2 0 X=0， S1 SCF 0 MD0， P×SCB×a0 Y=0， SCB SCF 0 SCB P S1 SCB ·P0.444P NAFAPANBFBB4-5解：取套钩为研究对象X=0， NA NB0MA=0， NB bFB dPl0MB=0， NA bFA dPl0 补充方程 FA sNA ， FB sNB NANB F·NAFAAXGYGBG l10cm 100mm4-6解：以整体为研究对象可只 FWNAFAAWNDFDD 以砖、架AGB为研究对象 对砖 X0， NA ND0Y0， FA FD W0补