河南省郑州市高一数学下学期期末试卷(含解析)

1、2015-2016学年河南省郑州市高一（下）期末数学试卷5分，共60分。在每小题给出的四个选项中，只有一、选择题本大题共12小题，每小题一项是符合题目要求的2.某商场想通过检查发票存根及销售记录的1.sin780°等于()2啾快速估计每月的销售总额，采取如下方法:从某本发票的存根中随机抽一张，如15号，然后按序往后将65号，115号，165号，发票存根上的销售额组成一个调查样本.这种抽取样本的方法是（）A.抽签法B.随机数法C.系统抽样法D.其他方式的抽样3 .已知扇形的半径为2,面积为4,则这个扇形圆心角的弧度数为（）A.-;B.2;C.2D.24 .从甲乙两个城市分别随机抽取16

2、台自动售货机，对其销售额进行统计，统计数据用茎叶图表示（如图所示），设甲乙两组数据的平均数分别为算甲，x乙，中位数分别为m甲，m乙,甲乙A.万用乙，m甲m乙B.C.K甲乂乙，m甲m乙D.M甲x乙，m甲vm乙5.把函数y=sinx（xCR）图象上所有点的横坐标缩短到原来的倍（纵坐标不变），再把4!图象上所有的点向左平行移动;二个单位长度，得到的图象所表示的函数是（）兀万兀A.y=sin(2x(xCR)B.y=sin(1(xCR)3z6兀2兀C.y=sin(2x+-)(xCR)D.y=sin(2x+生)(xCR)JJ6.执行如图所示的程序框图，若输入x的值为2,则输出的x值为()二二2"

3、1/输入工/冷 出-1A. 25B. 24C. 23D. 227.函数y=si n(2工I的一个递减区间为（）8.函数y=Asin （x+（） （3>0, |（）|<-;丁，xC R）的部分图象如图所示，则函数表达C.A.B .D.10.在直角 ABC 中，/BCA=90 ,CA=CB=1P为AB边上的点且 =入AB,若CF?超RPA?PB则入的取值范围是（)A.211C.亍-D.,啊)9.27U 1兀已知 tan ( a + 3 ) -, tan ( 3 ) q,那么 tan ( a 4)等于()A.H % ,兀 3兀 D-|(->A. y= 4sin)B. y=4sin

4、(Vx-RFx-C. y= 4sin()D. y=4sin (一 ox-"x+等）B. 13)C开始11.已知A为4ABC的最小内角，若向量全(cos2A,sin2A),=(12COSA41sin2A_2),则的取值范围是(A. ( - 8，三)B. (T,去)C.；)D.-,+°0)12.已知P、M N是单位圆上互不相同的三个点，且满足 ( )商1二1 一而| ,则可痛的最小值是A. - -B. -C.42D. 一 1二、填空题(本大题共2小题，每小题5分，共20分，将答案填在答题卡上的相应位置)13 .已知：，区均为单位向量，vgE>=60°,那么IW+

5、3EI=.14 .如图所示，四个相同的直角三角形与中间的小正方形拼成的一个边长为2的大正方形,4兀若直角三角形中较小的锐角9一一，现在向该正方形区域内随机地投掷一枚飞镖，飞镖落在小正方形内概率是15 .求函数f(x)=sinx+cosx+sinxcosx的值域.16 .f(x)=3sin(-"x+二),若实数m满足f(卜产+2说3)>f(J-),则m的取值范围是.三、解答题：本大题共6小题，共70分。解答应写出文字说明，证明过程或演算步骤17 .已知：口口是同一平面内的三个向量，其中导(1,2)(1)若1胃=2后且飞/鼻，求工的坐标；若|讣粤，且；+2E与2-E垂直，求鼻与1的

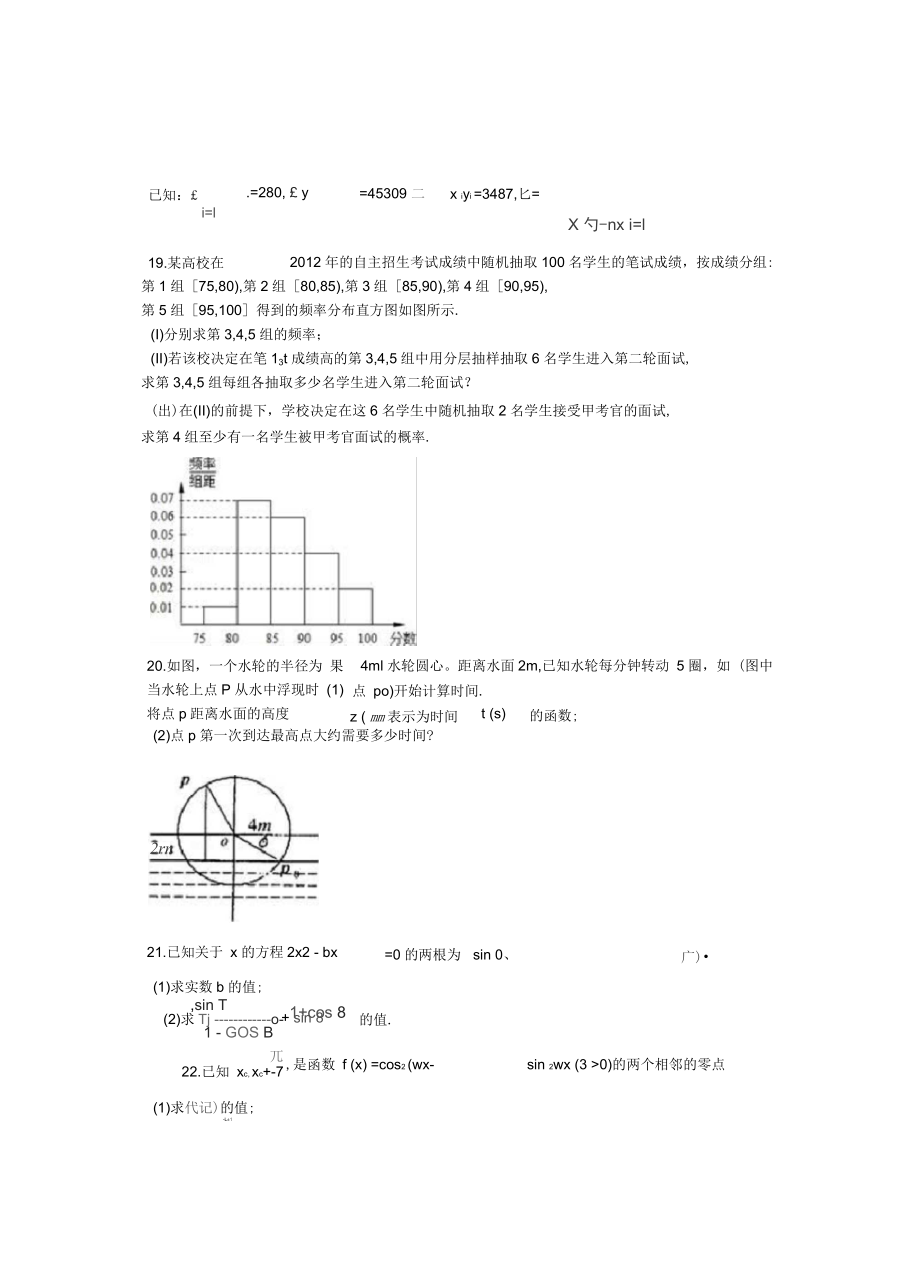
6、夹角0.18 .某个体服装店经营某种服装，在某周内获纯利y(元)与该周每天销售这种服装件数x之间的一组数据关系如下表x3456789y66697381899091(1)求纯利y与每天销售件数x之间的回归方程；(2)若该周内某天销售服装20件，估计可获纯利多少元？已知：£i=l.=280, £ y=45309 二x iyi =3487,匕=X 勺-nx i=l19.某高校在2012年的自主招生考试成绩中随机抽取100名学生的笔试成绩，按成绩分组:第1组75,80),第2组80,85),第3组85,90),第4组90,95),第5组95,100得到的频率分布直方图如图所示.(I

7、)分别求第3,4,5组的频率；(II)若该校决定在笔13t成绩高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试,求第3,4,5组每组各抽取多少名学生进入第二轮面试？(出)在(II)的前提下，学校决定在这6名学生中随机抽取2名学生接受甲考官的面试,求第4组至少有一名学生被甲考官面试的概率.20.如图，一个水轮的半径为 果当水轮上点P从水中浮现时 (1)将点p距离水面的高度4ml水轮圆心。距离水面2m,已知水轮每分钟转动 5圈，如 (图中点 po)开始计算时间.z ( mm表示为时间t (s)的函数;(2)点p第一次到达最高点大约需要多少时间?2rn21.已知关于 x的方程2x2 - bx

8、=0的两根为sin 0、广)(1)求实数b的值;,sin T(2)求Tjo-1 - GOS B兀22.已知 xc, xc+-71+cos 8+ sin 8的值.,是函数 f (x) =cos2 (wx-sin 2wx (3 >0)的两个相邻的零点(1)求代记)的值;-L±1m的取值范围.(2)若对WxE10,都有|f(x)-m|wi,求实数2015-2016学年河南省郑州市高一（下）期末数学试卷参考答案与试题解析一、选择题本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的1.sin780°等于（）【考点】运用诱导公式化简求值.【

9、分析】利用诱导公式，特殊角的三角函数值即可化简求值得解.【解答】解：sin780°=sin（2X360°+60°）=sin60°=士故选：B.2 .某商场想通过检查发票存根及销售记录的2快速估计每月的销售总额，采取如下方法：从某本发票的存根中随机抽一张，如15号，然后按序往后将65号，115号，165号，发票存根上的销售额组成一个调查样本.这种抽取样本的方法是（）A.抽签法B.随机数法C.系统抽样法D.其他方式的抽样【考点】系统抽样方法.【分析】本题所给的抽样的方法符合系统抽样的过程，分组时每50个个体一组，从第一组抽到15号，后面的号依次加50,得到整

10、个样本.【解答】解：二.总体的个体比较多，抽样时某本50张的发票存根中随机抽一张，如15号，这是系统抽样中的分组，然后按序往后将65号，115号，165号，发票上的销售额组成一个调查样本.样本间隔相同，.这种抽取样本的方法是系统抽样故选C.3 .已知扇形的半径为2,面积为4,则这个扇形圆心角的弧度数为（）A.仃B.2<3C.2叵.2【考点】扇形面积公式.【分析】半径为r的扇形圆心角的弧度数为“，则它的面积为Sar2,由此结合题中数据，建立关于圆心角的弧度数”的方程，解之即得该扇形的圆心角的弧度数.【解答】解：设扇形圆心角的弧度数为a,12112则扇形面积为S=7J"ar=77a

11、X2=4解得：a=2故选：D.4.从甲乙两个城市分别随机抽取16台自动售货机，对其销售额进行统计，统计数据用茎叶图表示(如图所示)，设甲乙两组数据的平均数分别为工甲，直乙，中位数分别为m甲，m乙,S6?007 8023371244 S23 8S84C0i7522SOO1m甲m乙B.直用乙，m甲vm乙C.K甲二乂乙，m甲m乙D.M甲x乙，m甲vm乙【考点】茎叶图；众数、中位数、平均数.【分析】直接求出甲与乙的平均数，以及甲与乙的中位数，即可得到选项.【解答】解：甲的平均数G甲5+6+8+10+10+14+18+18+22+25+27+30+3。+38+41+4：=345116HT，乙的平均数乙=

12、1 0 12£ 8+2 计 22+2 3+23+27+31+32434+3 如 38+ 4 2M3 的1645716所以|4v中甲的中位数为20,乙的中位数为29,所以m甲vm乙故选：B.5.把函数y=sinx(xCR)图象上所有点的横坐标缩短到原来的/倍(纵坐标不变)，再把图象上所有的点向左平行移动二个单位长度，得到的图象所表示的函数是()bK|xKlA.y=sin(2x(xCR)B.y=sin(-I-：)(xCR)Jzb7T2兀C.y=sin(2x+)(xCR)D.y=sin(2x+7)(xCR)JJ【考点】函数y=Asin(wx+()的图象变换.【分析】先根据横坐标缩短到原来的

13、4倍时w变为原来的2倍进行变换，再根据左加右减的原则进行平移，即可得到答案.【解答】解：由y=sinx的所得图象上所有点的横坐标缩短到原来的/倍得到y=sin2x,兀五|7TI再把图象向左平行移动7一个单位得到y=sin2(x+-1)=sin(2x+一丁)，故选C6.执行如图所示的程序框图，若输入x的值为2,则输出的x值为（A.25B.24C.23D.22【考点】循环结构.【分析】分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知：该程序的作用是计算x,并输出x值.【解答】解：程序运行过程中，各变量的值如下表示：是否继续循环xn循环前/21第一圈是52第二圈是113第三圈是234第四

14、圈否此时输出的x值为23故选C.I的一个递减区间为（）H7T.,A.C1一【考点】正弦函数的单调性.【分析】先根据正弦函数的单调性求得函数y的单调递减时2x-亍的范围，进而求得范围得到了函数的单调递减区间，然后结合选项进行判定即可.【解答】解：由正弦函数的单调性可知y=sin的单调减区间为2k兀+Lxwk兀+得兀kJ(kJ)而(兀2n-T)?kw-故选A.8.函数y=Asin(3x+()(3>0Hl<冗2，xCR)的部分图象如图所示，则函数表达)0A.y=4sinC.y=4sin兀(-x-死7T)B.y=4sin(x8一x+8TT)D.y=4sin(-x+8【考点】由y=Asin（

15、3x+（）的部分图象确定其解析式.co,由特殊点的坐标求出。的值,【分析】由函数的图象的顶点坐标求出A,由周期求出可得函数的解析式.【解答】 解：由函数的解析式可得 A=4,=6+2,再根据sin (- 2) x2) x+ 4 =k 兀，k C z,再结合 |（f）| v7T2- y=4sin (7T 7U1P+T),故选：D.9.已知 tan (a + 3)tan ( 3 7UT，那么tan （ a +A.13ISC.22D.【考点】两角和与差的正切函数.【分析】把已知的条件代入t©（口+7）=tan（7ET）尸tan(Cl+P)-tanCP-兀4)l+tan(q+S)ran(B-

16、卷),运算求得结果2冗【解答】解：:已知转，tan（B-S44tanl也十口)=tan(a+3)-(37T4)=tan(CH-g)-tan(3-兀4)Htan(G+f)*tan(Hq2_2彳1X-4 故选C.2210.在直角ABC中，/BCA=90,CA=CB=1P为AB边上的点且向=入彘，若行而痂则入的取值范围是（A.1B.r 1 1+V2 in r1C. 一，-3-±Ld.【考点】 【分析】值范围.【解答】向量在几何中的应用；平面向量数量积的运算.把三角形放入直角坐标系中，求出相关点的坐标，利用已知条件即可求出解：直角 ABC 中，/ BCA=90 , CA=CB=1入的取以C为

17、坐标原点CA所在直线为x轴，CB所在直线为y轴，如图:C(0, 0), A (1,0), B(0, 1),1)2入+入2入.解得:入 而二d一入，入），市二（工.1，入）.:CP?赶产PA?FB.入T+2入：2入2-4入+1W0,2-J20,12-2入 111.已知A为ABC的最小内角，若向量二二(cos2A,sin2A),1=(z,=),cas2A41sinA-2则之*三的取值范围是()1191A.(8,寺B.(1,时C.昌去)D.zAb2【考点】平面向量数量积的运算.【分析】利用向量的数量积得出；- =cos2A?" +sincos Afi2A?1sin2A-23=2+si n

18、k 2AS (0,勺，再利用单调性求解即可.【解答】 解：:A为 ABC的最小内角，若向量 = (cos2A, sin 2A), E= (cosKn?A-2)' . t r =cos2A?+sin 2A?"cos2A+1笃in2A一 23=2+sin2- 2,AC (0根据函数解析式判断为减函数3 1，最大值为：2-,(此值取不着)2最小值为：斐7= -45一 一2 1，a + h的取值范围=，)故选：C12.已知P、M N是单位圆上互不相同的三个点，且满足|西|二|百5|,( )则而标的最小值是A.1B.4C【考点】平面向量数量积的运算.【分析】由题意可得，点P在MN的垂直

19、平分线上，不妨设单位圆的圆心为O(0,0),点P(0, 1),点 M (X1, yO,则点 N ( X1,yO,由戈1 4尸1上二1得而和=2乎1出最小值.【解答】解：由题意可得，点P在MN的垂直平分线上，不妨设单位圆的圆心为O(0,0),点P(0,1),点M(X1,yj,则点N(-X1,yO,1Wy1V1守产（x1,yi1),"pn=(xi,yi1),22町斗力二1Pi?PN=-工/+-2-2%+樽1-勾1=2卬一/）一工,.当yi=y时百？而的最小值是_=士1仁1故选：B.二、填空题（本大题共2小题，每小题5分，共20分，将答案填在答题卡上的相应位置）13 .已知：，5均为单位向

20、量，va,b>=60°,那么|彳+3|=sqrt13.【考点】平面向量数量积的运算.【分析】a另均为单位向量，则它们的模都是1,要求向量值+3£|的模，可求其平方，然后利用向量模的平方等于向量的平方，展开后再利用平面向量的数量积运算求解.【解答】解：:a,另均为单位向量，11a|b|二1.又V1,1>=60二一"一二，.：iJ,I，二:I-二、.:-='|'I，：.广,-=I7；-=/13故答案为：a/13.14 .如图所示，四个相同的直角三角形与中间的小正方形拼成的一个边长为2的大正方形,c7U若直角三角形中较小的锐角9一一，现在向该

21、正方形区域内随机地投掷一枚飞镖，飞镖落在小正方形内概率是1-fracsqrt32.【考点】几何概型.【分析】根据几何概率的求法：一次飞镖扎在中间小正方形区域（含边线） 区域的面积与总面积的比值.【解答】解：观察这个图可知：大正方形的边长为2,总面积为4,而阴影区域的边长为 近T,面积为4 273；故飞镖落在阴影区域的概率 "运二1 - 叵,42故答案为：一乌.的概率就是阴影15.求函数 f （x） =sinx+cosx+sinxcosx 的值域.【考点】函数的值域；三角函数的最值.兀【分析】利用换元法令t=sinx+cosx= dgsin （x-j）,从而可得-J2wtw，亍,上上

22、一 1t* _ 21sinxcosx= ，从而可得 f (x) =sinx+cosx+sinxcosx=t+ -= (t +2t - 1) =ri (t+1 )22222-1;从而求函数的值域.【解答】 解：令 t=sinx+cosx= V_2sin (x+7TT),贝卜JwtwJ，t2=1+2sinxcosx，贝U sinxcosx=t2-l2贝Uf(x)=sinx+cosx+sinxcosx=t+=歹(t+1)-1；riL-a-r/2<t<Vs,(t+1)2-1<-+yi；故函数f(x)=sinx+cosx+sinxcosx的值域为1,=+&.1QITr=-,16

23、. f (x) =3sin（一百斤丁），若实数m满足f（寸一产+2说3）f（-即2+4），则R-JJ_Um的取值范围是-1,frac12)【考点】正弦函数的图象.【分析】由二次函数性质可知0*正京荷2,0&q挤一,根据正弦函数的性质可得f（x）在0,2上单调递减，于是0代加2+293）皿”.W2,利用二次函数性质解出m的范围.【解答】解：f（x）=3sin（-L+¥）=-3sin）,实数m满足f（J一1r之+2说3）510510vmiuhu>f（J-#+4），JTx37TJT令+2k兀w<2k兀+解得一兀+10k%WxW4Tt+10kTt,2510Z2上是减.f(

24、x)的单调减区间为+10kTt,4兀+10卜兀,kZ,/.f(x)在区间0,函数.故不等式的解集为口十4）0，求得-、一口+211rt3<-m"+4故答案为：-1,；）.三、解答题：本大题共6小题，共70分。解答应写出文字说明，证明过程或演算步骤17.已知：、后、信是同一平面内的三个向量，其中导（1,2）（1）若1c|=2寸亏，且立,求3的坐标；（2）若|母=萼，且；+2芯与2-E垂直，求鼻与芯的夹角九【考点】数量积判断两个平面向量的垂直关系；平面向量共线（平行）的坐标表示；数量积表示两个向量的夹角.Ty-2x=0【分析】（1）设二6,V）,由|A=2v忌且W/G,知05r,由

25、此能求出7的坐标.=20电*11!B,gi-*"!（2）由（a+2b）l（2a-l）,知Q+2b”2Lb）二。，整理得口产,故<La-P1:皿日二I二1,由此能求出W与E的夹角0.周小I【解答】解：（1）设台&y）,Ic|=2'/S,且亡/a,/-2s=0解得jy-q或'二，二20,、y=-4'故/4）或三02,-4）（：+2.）1（2；-工），Ca+2b)-(21-b)=0即W+3；用-乐4q，rfC2X5+3ab_2*彳二0，整理得4E二一二，c：as 6 -.1 dbl '345666697381求纯利y与每天销售件数 若该周内某天

26、销售服装y(1)(2)又ee0,.9=ti.18 .某个体服装店经营某种服装，在某周内获纯利y（元）与该周每天销售这种服装件数之间的一组数据关系如下表789899091x之间的回归方程；20件，估计可获纯利多少元?已知：E-=280,£y=45309,_xiyi=3487,卜=【考点】【分析】方程；（2）把【解答】线性回归方程.（1）设回归直线方程为x=20代入回归方程求出:尸！，x+3,根据题意确定出式与鼻的值，即可确定出所求回归Q的值，即可确定出获利的钱数.解：（1）设回归直线方程为广bx+w，.£xi2=280,£1=1yi2=45309,£xiy

27、i=3487,i=l-559工=6，T=二一348T-X-280-7X36-，回归直线方程为y=4.75x+51.36;（2）当x=20时，=4.75X20+51.36=146.则某天的销售量为20件时，估计这天可获纯利大约为146元.1332855976X4.75=51.36,19 .某高校在2012年的自主招生考试成绩中随机抽取100名学生的笔试成绩，按成绩分组:第1组75,80),第2组80,85),第3组85,90),第4组90,95),第5组95,100得到的频率分布直方图如图所示.(I)分别求第3,4,5组的频率；(II)若该校决定在笔13t成绩高的第3,4,5组中用分层抽样抽取6

28、名学生进入第二轮面试，求第3,4,5组每组各抽取多少名学生进入第二轮面试？(出)在(II)的前提下，学校决定在这6名学生中随机抽取2名学生接受甲考官的面试，求第4组至少有一名学生被甲考官面试的概率.【考点】频率分布直方图；古典概型及其概率计算公式.【分析】(I)根据频率分步直方图的性质，根据所给的频率分步直方图中小矩形的长和宽，求出矩形的面积，即这组数据的频率.(II)由上一问求得频率，可知3,4,5组各自所占的比例样，根据分层抽样的定义进行求解；(出)由题意知变量E的可能取值是0,1,2,该变量符合超几何分布，根据超几何分布的概率公式写出变量的概率，写出这组数据的分布列从而求出P(E>

29、1)的概率；【解答】解：(I)根据所给的频率分步直方图中小正方形的长和宽，得到第三组的频率为0.06X5=0.3;第四组的频率为0.04X5=0.2;第五组的频率为0.02X5=0.1.(n)由题意知本题是一个等可能事件的概率，由(I)可知第三，四，五组的频率分别为：0.3,0.2,0.1则分层抽样第3,抽取的人数为：瞿*6=3Q.2第4组抽取的人数为：7rrX6=20.85组每组抽取的人数为：然X6=1;u.b(出)学校决定在这6名学生中随机抽取2名学生接受甲考官的面试，由题意知变量E的可能取值是0,1,2该变量符合超几何分布，厂工一i.P(E=i)=2-(i=0,1,2)C6分布列是qQL

30、2尸8151IS。-二151515520.如图，一个水轮的半径为4ml水轮圆心。距离水面2m,已知水轮每分钟转动5圈，如果当水轮上点P从水中浮现时（图中点.）开始计算时间.（1）将点p距离水面的高度z（m）表示为时间t（S）的函数；（2）点p第一次到达最高点大约需要多少时间？【考点】已知三角函数模型的应用问题.【分析】（1）先根据z的最大和最小值求得 A和B,利用周期求得co,当 而求得。的值，则函数的表达式可得；x=0 时，z=0,进（2）令最大值为 6,即z=4sinn 7i-t ）+2=6可求得时间.【解答】解：（1）依题意可知z的最大值为6,最小为-2,A=4B=2op每秒钟内所转过的角为（5乂2冗60得z=4sin(丁t+小)十2,故所求的函数关系式为z=4sin£7L兀+2,71(2)令z=4sinj-工一丁+2=6,得sin一-丁=1JT兀死取丁一一二二一故点P第一次到达最高点大约需要4S.21.已知关于 x的方程2x2 - bx-y=0 的两根为 sin 0、cos 0 , 0 (7T 43K丁).（1）求实数b的值;1+cos8的值.【考点】同角三角函数基本关系的运用