最值问题(费马点)_第1页
最值问题(费马点)_第2页
最值问题(费马点)_第3页
最值问题(费马点)_第4页
最值问题(费马点)_第5页
免费预览已结束，剩余1页可下载查看

下载本文档

版权说明：本文档由用户提供并上传，收益归属内容提供方，若内容存在侵权，请进行举报或认领

文档简介

1、精品文档最值问题2 （费马点）PA+PB+PC勺最小值.2、已知：P是边长为1的等边三角形 ABC内的一点，求 PA+PB+PC勺最小值.1欢四下载精品文档5欢6载小伟遇到这样一个问题:AB=2, AC=4,以BC为边在ABP图1如图 1,在 ABC（其中/ BAC个可以变化的角）中, BC的下方作等边 PBC求AP的最大值。A'ACBC图2小伟是这样思考的：利用变换和等边三角形将边的位置重新组合.他的方法是以点B为旋转中心将 4AB斑时针旋转60°得到AABC,连接A'A,当点A落在A'C上时，此题可解（如图2）.请你回答：AP的最大值是参考小伟同学思考问题

2、的方法，解决下列问题:.如图3,等腰Rt ABC边AB=4,P为4ABC内部一点,则AP+BP+CP勺最小值是（结果可以不化简）4、(朝阳二模)阅读下列材料:小华遇到这样一个问题，如图1, ABC43, / ACE=30o,BG=6, AC=5,在 ABC内部有一点P,连接PA PB PC求PA+P9PC的最小值.图1图2小华是这样思考的：要解决这个问题，首先应想办法将这三条端点重合于一点的线段分 离，然后再将它们连接成一条折线，并让折线的两个端点为定点，这样依据“两点之间，线 段最短”，就可以求出这三条线段和的最小值了.他先后尝试了翻折、旋转、平移的方法， 发现通过旋转可以解决这个问题.他的

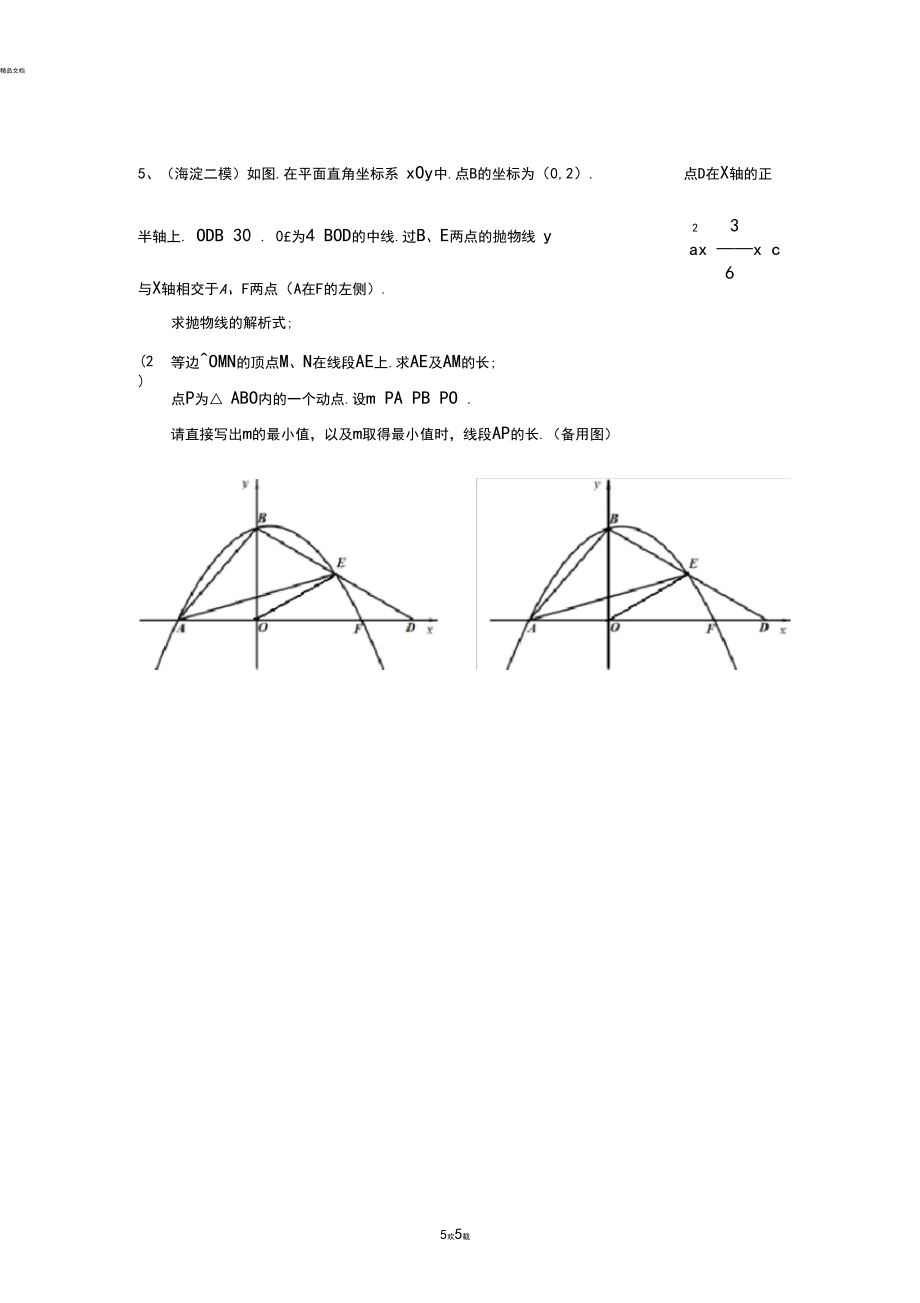
3、做法是，如图 2,将4APC绕点C顺时针旋转60o, 得至iJEDC连接PD BE,则BE的长即为所求.(1)请你写出图2中，PAP8PC的最小值为 ；(2)参考小华的思考问题的方法，解决下列问题：如图3,菱形ABCDK / ABC60。，在菱形 ABC咕部有一点 P,请在图3中画 出并指明长度等于 PA+P9PC最小值的线段(保留画图痕迹，画出一条即可)； 若中菱形ABCD勺边长为4,请直接写出当 PA+PBPC值最小时PB的长.5、（海淀二模）如图.在平面直角坐标系 xOy中.点B的坐标为（0,2）.点D在X轴的正半轴上. ODB 30 . 0£为4 BOD的中线.过B、E两点的抛物线 y23ax x c6与X轴相交于A、F两点（A在F的左侧）.求抛物线的解析式;(2)等边OMN的顶点M、N在线段AE上.求AE及AM的长;点P为 ABO内的一个动点.设m PA PB PO .请直接写出m的最小值，以及m取得最小值时，线段AP的长.（备用

人人文库> 全部分类> 应用文书 > 作业报告

温馨提示

  • 1. 本站所有资源如无特殊说明，都需要本地电脑安装OFFICE2007和PDF阅读器。图纸软件为CAD,CAXA,PROE,UG,SolidWorks等.压缩文件请下载最新的WinRAR软件解压。
  • 2. 本站的文档不包含任何第三方提供的附件图纸等，如果需要附件，请联系上传者。文件的所有权益归上传用户所有。
  • 3. 本站RAR压缩包中若带图纸，网页内容里面会有图纸预览，若没有图纸预览就没有图纸。
  • 4. 未经权益所有人同意不得将文件中的内容挪作商业或盈利用途。
  • 5. 人人文库网仅提供信息存储空间，仅对用户上传内容的表现方式做保护处理，对用户上传分享的文档内容本身不做任何修改或编辑，并不能对任何下载内容负责。
  • 6. 下载文件中如有侵权或不适当内容，请与我们联系，我们立即纠正。
  • 7. 本站不保证下载资源的准确性、安全性和完整性, 同时也不承担用户因使用这些下载资源对自己和他人造成任何形式的伤害或损失。

最新文档

评论

0/150

提交评论