中考数学定心模拟试卷含解析1

1、2016年河南省中考数学定心模拟试卷一、选择题（每小题3分，共24分）下列各小题均有四个答案，其中只有一个是正确的1. -J的相反数是（）OAccc1A.-6B.6C.-|-r|D.1I*I2.如图所示的几何体的左视图是（）3 .下列各式计算正确的是()A.a3?a=a4B.2a3+a3=3a6C.(a2b)3=a6b3D.(b+2a)(2ab)=b2-4a24 .如图，直线EF分别与直线AB>CD相交于点GG,已知/1=72=40°,GI平分/HGB交直线CD于点I,则/3=（A.40°B.50°C.55°D,70°5 .关于x的一元二

2、次方程|m|x2-2x+1=0有两个不相等的实数根，则m的取值范围是（）A.1vm<1B.1vm<1且m0C.m>1D.m<1且m06 .在一次体育达标测试中，小明所在小组的六位同学的立定跳远成绩如下（单位：成：2.00,7 .11,2.21,2.15,2.20,2.17,那么这组数据的中位数是（）A.2.16B,2.15C,2.14D,2.137 .如图，在RtABC中，/C=90,AC=4,BC=3点D是AC的中点，连接BD,按以下步骤作图：分别以B,D为圆心，大于BD的长为半径作弧，两弧相交于点P和点Q作直线PQ交AB于点E,交BC于点F,则BF=（）8 .如图，

3、4ABC是边长为4cm的等边三角形，动点P从点A出发，以2cm/s的速度沿ZCAB运动，到达B点即停止运动，过点P作PD±AB于点D,设运动时间为x(s),4ADP的面积为y(cm2),则能够反映y与x之间函数关系的图象大致是()二、填空题(每小题3分，共21分)9 .计算：+(tt-2)0=.AB210 .如图，l1/12/13,两条直线与这三条平行线分别交于点A、B、C和D、E、F,已知前二万,11 .不等式组J62算3的最大整数解是.L-12 .已知二次函数y=x2+(m-2)x+1,当x>1时，y随x的增大而增大，则m的取值范围是.13 .现有四张完全相同的卡片，上面分

4、别标有数字0,1,2,3,把卡片背面朝上洗匀，然后从中随机抽取两张卡片组成一个两位数，则这个两位数是偶数的概率是.14 .如图，正方形ABCDi长为3,将正方形ABCD§点B顺时针旋转30°,得到正方形3ABCD',则图中阴影部分的面积是区冗.15 .如图，在矩形ABCD,AB=5,BC=3点E为射线BC上一动点，将ABE沿AE折叠,得到AB'E.若B'恰好落在射线CD上，则BE的长为号三、解答题(本大题共16.先化简，再求值：8个小题，满分75分)K-+1K_1V7V?氐2+(，一一算22富+1)，然后一WxW的范围内选取一个合适的整数作为x的值代

5、入求值.17 .如图，以ABC的边AB为直径的。交AC边于点D,且过点D的。的切线DE平分BC边，交BC于点E.(1)求证：BC是。的切线；(2)当/A=时，以点QB、E、D为顶点的四边形是正方形；(3)以点QB、E、D为顶点的四边形(可能、不可能)为菱形.C18 .国家环保局统一规定，空气质量分为5级.当空气污染指数达0-50时为1级，质量为优；51-100时为2级，质量为良；101-200时为3级，轻度污染；201-300时为4级，中度污染；300以上时为5级，重度污染.某城市随机抽取了2015年某些天的空气质量检测结果，并整理绘制成如图两幅不完整的统计图.请根据图中信息，解答下列各题：(

6、1)本次调查共抽取了天的空气质量检测结果进行统计；(2)补全条形统计图；(3)扇形统计图中3级空气质量所对应的圆心角为。；(4)如果空气污染达到中度污染或者以上，将不适宜进行户外活动，根据目前的统计，请你估计2015年该城市有多少天不适宜开展户外活动.空气质量等级天数统计图空气质量等级天数占所抽取天数百分比统计图y=(k>0)相交于点A、B,点19 .如图，在平面直角坐标系xOy中，直线y=mx+1与双曲C在x轴正半轴上，点D(1,-2),连结OAODDCAC四边形AODCJ菱形.(1)求k和m的值；(2)根据图象写出反比例函数的值小于2时x的取值范围；(3)设点P是y轴上一动点，且Sa

7、oa=S菱形oacd求点P的坐标.20 .如图，小明站在河岸上的E点，看见正对面的河岸边有一点C,此时测得C点的俯角是30。.若小明的眼睛与地面的距离DE是1.6米，BE=1米，BE平行于AC所在的直线，迎水坡的坡度i=4:3,坡长AB=10米，求河宽AC.(结果保留整数，参考数据：加=1.73)21 .某批发市场有中招考试文具套装，其中A品牌的批发价是每套20元，B品牌的批发价是每套25元，小王需购买AB两种品牌的文具套装共1000套.(1)若小王按需购买A、B两种品牌文具套装共用22000元，则各购买多少套？(2)凭会员卡在此批发市场购买商品可以获得8折优惠，会员卡费用为500元.若小王购

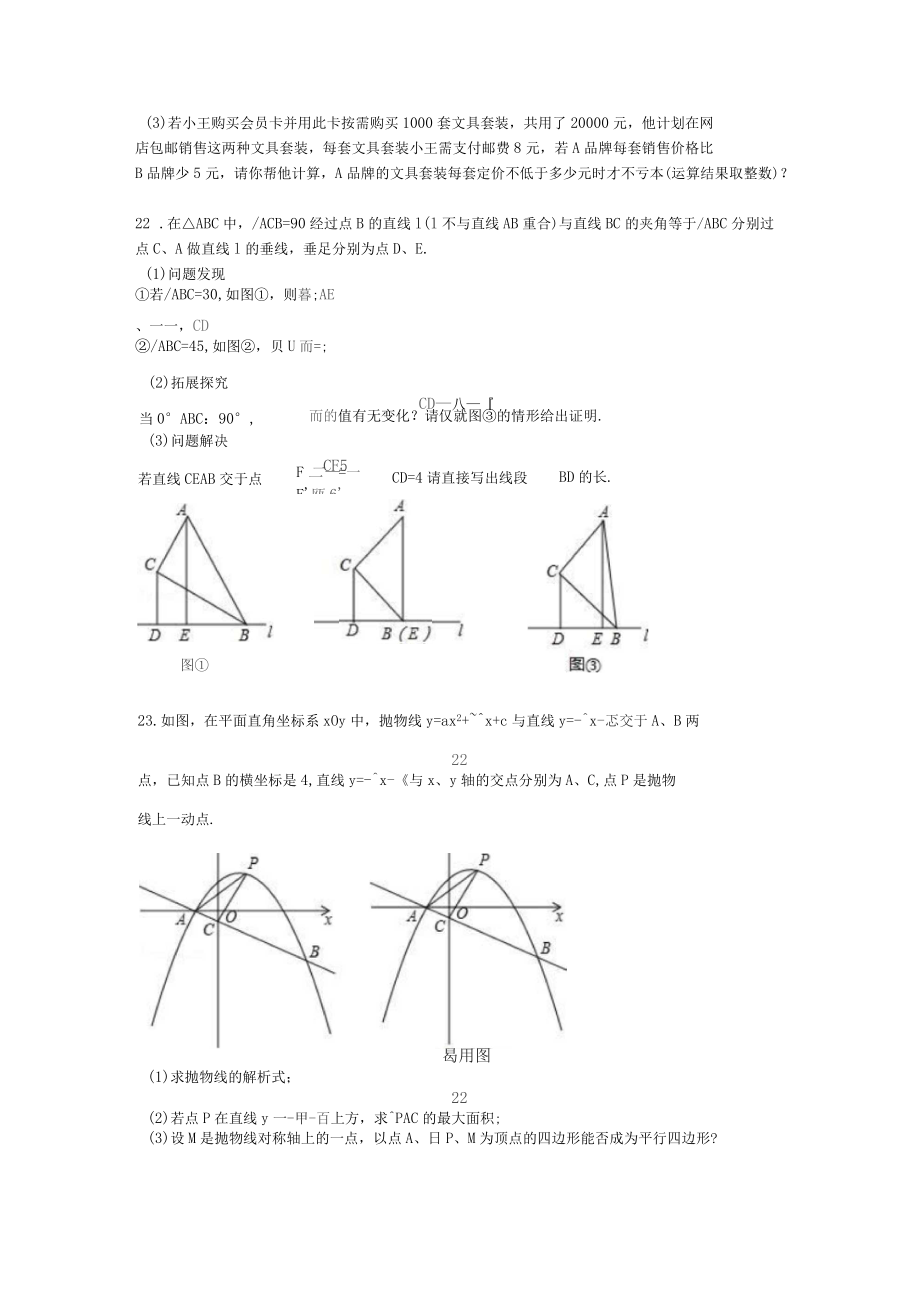
8、买会员卡并用此卡按需购买1000套文具套装，共用了y元，设A品牌文具套装买了x包,请求出y与x之间的函数关系式.(3)若小王购买会员卡并用此卡按需购买1000套文具套装，共用了20000元，他计划在网店包邮销售这两种文具套装，每套文具套装小王需支付邮费8元，若A品牌每套销售价格比B品牌少5元，请你帮他计算，A品牌的文具套装每套定价不低于多少元时才不亏本(运算结果取整数)？22 .在ABC中，/ACB=90经过点B的直线l(l不与直线AB重合)与直线BC的夹角等于/ABC分别过点C、A做直线l的垂线，垂足分别为点D、E.(1)问题发现若/ABC=30,如图，则暮;AE、一一，CD(2)拓展探究当

9、0°ABC：90°,/ABC=45,如图，贝U而=;CD八而的值有无变化？请仅就图的情形给出证明.(3)问题解决若直线CEAB交于点CF5F二=一F'瓯6'CD=4请直接写出线段图BD的长.23.如图，在平面直角坐标系xOy中，抛物线y=ax2+x+c与直线y=-x-忑交于A、B两22点，已知点B的横坐标是4,直线y=-x-与x、y轴的交点分别为A、C,点P是抛物线上一动点.曷用图(1)求抛物线的解析式；22(2)若点P在直线y一-甲-百上方，求PAC的最大面积;(3)设M是抛物线对称轴上的一点，以点A、日P、M为顶点的四边形能否成为平行四边形?若能，求出点

10、P的坐标；若不能，请说明理由2016年河南省中考数学定心模拟试卷参考答案与试题解析一、选择题(每小题3分，共24分)下列各小题均有四个答案，其中只有一个是正确的1. -1的相反数是()6Accc1A.-6B.6C.-|-|D.高oo【考点】相反数；绝对值.【分析】用相反数数的意义直接确定即可.【解答】解：-的相反数是4，66故选D.2 .如图所示的几何体的左视图是()【考点】简单几何体的三视图.【分析】找到从左面看所得到的图形即可，注意所有的看到的棱都应表现在左视图中.【解答】解：从左往右看，易得一个长方形，正中有一条横向实线，故选：C.3 .下列各式计算正确的是()A.a3?a=a4B.2a

11、3+a3=3a6C.(a2b)3=a6b3D.(b+2a)(2ab)=b2-4a2【考点】平方差公式；合并同类项；同底数哥的乘法；哥的乘方与积的乘方.【分析】根据同底数哥的乘法法则、合并同类项、积的乘方、平方差公式的计算法则进行计算，逐一排除即可.【解答】解：A、a3?a=a4,故选项正确；B>2a3+a3=3a3,故选项错误；C(-a2b)3=a6b3,故选项错误；D(b+2a)(2a-b)=(2a+b)(2a-b)=4a2-b2,故选项错误.故选：A.4 .如图，直线EF分别与直线AB>CD相交于点GG,已知/1=72=40°,GI平分/HGB交直线CD于点I,则/3

12、=()EDA.40°B.50°C.55D.70°【考点】平行线的判定与性质.GI平分/HGBAB/CD从而【分析】根据邻补角的性质与/1=50°,求得/BGH=180-40°=140°,由交直线CD点I,得出/BGI的度数，根据同位角相等，两直线平行，得到利用平行线的性质，求得/3的度数.【解答】解：.一/1=50°,BGH=180-40°=140°,.GI平分/HGB/BGI=70°,1 =/2,.AB/CD（同位角相等，两直线平行），3=/BGI=70°（两直线平行，内错角相等）.

13、故选D.EB【解答】解：这组数据按照从小到大的从小到大的顺序排列为：2.00,2.11,2.15,2.17,2.20,2.21,最中间的数为第3个数和第4个数，所以中位数为(2.15+2.17)+2=2.16.故选A.7.如图，在RtABC中，/C=90,AC=4,BC=3点D是AC的中点，连接BD,按以下步骤作图：分别以B,D为圆心，大于£bD的长为半径作弧，两弧相交于点P和点Q作直线PQ交AB于点E,交BC于点F,则BF=(.5135A巳1CD-一【考点】作图一基本作图；线段垂直平分线的性质.【分析】连结DF,利用基本作图得到由EF垂直平分BD,贝UBF=DF设BF=x,贝UDF

14、=x,CF=3x,然后在RtDCF中利用勾股定理得到22+(3-x)2=x2,然后解方程即可.【解答】解：连结DF,由作法得EF垂直平分BD则BF=DF点D是AC的中点，CD=7AC=2,设BF=x,贝UDF=x,CF=3x,13在RtDCF中，22+(3x)2=x2,解得x=t，口.13即BF蓝8 .如图，4ABC是边长为4cm的等边三角形，动点P从点A出发，以2cm/s的速度沿ZCAB运动，到达B点即停止运动，过点P作PD±AB于点D,设运动时间为x(s),4ADP的面积为y(cm2),则能够反映y与x之间函数关系的图象大致是()C【考点】【分析】C.D.动点问题的函数图象.过点

15、P作PDLAB于点D,分类求出点P从A-C和从CB函数解析式，即可得到相应的函数图象.【解答】解：过点P作PD!AB于点D,4ABC是边长为4cm的等边三角形,贝UAP=2x,所示,当点P从A-C的过程中，AD=x，PD=/x,如右图12，一,(0WxW2),nrt11贝Uy=AD?PD=PD=(4x),PC=2x-4,如右图当点P从的过程中，BD=(8-2x)X=4-x,所示,V3C则ABC边上的高是：AC?sin60°=4X甘=2,y=SAABC-SaACP-Sabdp(2=/x4X2&»-4)乂续»(4-标如(47=-孚/+2百<x<4)

16、,故选B.二、填空题（每小题3分，共21分）9 .计算：一£+（71-2）0=-1.【考点】实数的运算；零指数哥.【分析】根据实数的运算顺序，首先计算乘方、开方，然后计算加法，求出算式%仁+（兀-2）0的值是多少即可.【解答】解：*黑+（兀-2）0=-2+1=-1故答案为：-1.,_AB210.如图，l1/12/13,两条直线与这二条平行线分别交于点A、B、C和D、E、F,已知击DC3ABDE77FF，再将已知数据代入求出即可【考点】平行线分线段成比例.【分析】直接利用平行线分线段成比例定理进而得出【解答】解:ABJDE32BCyDE_2DF=5,故答案为:11,不等式组。+的最大整

17、数解是116-2x>3【考点】一元一次不等式组的整数解.再求出不等式组的解集，然后在【分析】根据不等式的性质分别求出每一个不等式的解集,解集中找出最大整数即可.【解答】由得:初fx+i>o0斛：'x>-1,由得：XV1.5,.不等式组的解集是-1WXV1.5,.不等式组的最大整数解是1.故答案为1.12.已知二次函数y=x2+(m-2)x+1,当x>1时，y随x的增大而增大，则m的取值范围是尼0.【考点】二次函数的性质.【分析】根据二次函数的性质，利用二次函数的对称轴不大于1列式计算即可得解.【解答】解：抛物线的对称轴为直线x=丁=-m+1,当x12时，y的值随

18、x值的增大而增大，1 .7/m+K1,解得m0.故m的取值范围是m>0.故答案为：m户0.13.现有四张完全相同的卡片，上面分别标有数字0,1,2,3,把卡片背面朝上洗匀，然后从中随机抽取两张卡片组成一个两位数，则这个两位数是偶数的概率是_q_.【考点】列表法与树状图法.【分析】首先根据题意画出树状图，然后由树状图求得所有等可能的结果与这个两位数是偶数的情况，再利用概率公式求解即可求得答案.【解答】解：画树状图得：开始zT/KZ073013012共有9种等可能的结果，这个两位数是偶数的有5种情况,5这个两位数是偶数的概率是：§.5故答案为：百.14.如图，正方形ABCDi长为3

19、,将正方形ABCDg点B顺时针旋转30°,得到正方形3ABCD',则图中阴影部分的面积是了冗.nr【考点】【分析】影=$扇形DBDD【解答】解：如图,D1旋转的性质；正方形的性质.先根据正方形的性质求出BD再根据旋转得到/ABA=/DBD=30°,判断出S阴)S扇形ABA即可.B连接BD,BD,正方形ABCDfe长为3,.BD=3/2,正方形ABC四点B顺时针旋转30°,得到正方形ABCD',./ABA=/DBD=30°,3。”XJTXBI?30"XJIX（3n/2）S扇形DBD=360360S扇形ABA30aXKXAB230&

20、#176;X7TX93X3600360S阴影=S扇形DBD+SaABDSaaBD-S扇形ABA=S扇形DBD3n3冗3_一S扇形ABA=一=""JL15.如图，在矩形ABCN,AB=5,BC=3点得到AB'E.若B'恰好落在射线CD上，则E为射线BC上一动点，将ABE沿AE折叠,一5一BE的长为可或为.5,J?【考点】【分析】B日2+12,翻折变换(折叠问题)；矩形的性质.如图1,根据折叠的性质得到AB'=AB=5B'E=BE根据勾股定理得到BF=(3-5根据勾股定理得E2=CC+B'C：于是得到BE=1,如图2,根据折叠的性质得到A

21、B'=AB=5求得AB=BF=5到CF=4根据相似三角形的性质列方程得到CE=12,即可得到结论.【解答】解：如图1,二,将ABE沿AE折叠，得到ABE,.AB'=AB=5B'E=BE，CE=3BE,AD=3，DB=4,.B'C=1,B'BE2=(3-BE)2+1：一5 BE=:,如图2,二.将ABE沿AE折叠，得到AB'E, .AB'=AB=51. CD/AB,/1=/3,1 =/2,/2=/3,.AE垂直平分BB',.AB=BF=5.CF=4,1. CF/AB,.CEMABECtCE=ABBE?riCB即5=CE+S'

22、.CE=12,BE=15,，5综上所述：BE的长为：*或15,05八故答案为：三或15.靶三、解答题（本大题共8个小题，满分75分）Kk+LX-1V7<x<的范围内选取16 .先化简，再求值：K2-1+（X-1-空-2篡+1）,然后一个合适的整数作为x的值代入求值.【考点】分式的化简求值；约分；通分.x的值,【分析】先进行括号里面的减法运算，再进行加法运算求得结果，最后选择合适的代人所得结果计算求值.X_+LX_1【解答】解：原式=(f+1)G-1)+L1-(厂1)2三.(f+1)(x-1)x-1x-1X一:'二+Z-11+二-1=:'-+YL!Ix2+2x-币&a

23、mp;x&币,且x为整数，要使分式有意义，则x只能取2或-24-4当x=2时，原式=-T=04-1DE平分BC17 .如图，以ABC的边AB为直径的。交AC边于点D,且过点D的。的切线边，交BC于点E.(1)求证：BC是。的切线；(2)当/A=45°时,以点。BE、D为顶点的四边形是正方形；(3)以点OB、E、D为顶点的四边形不可能(可能、不可能)为菱形.C【考点】圆的综合题.【分析】（1）要证BC是。O的切线，就要证OBLBC,只要证/OBE=90即可，首先作辅助线，连接ODOE,由已知得OE为ABC的中位线，O曰AC,从而证得OD孽OBE推出/ODEWOBE又DE是。的切

24、线，所以得/OBE=90,即OBLBC,得证.（2）由题意使四边形OBED正方形，即得到OD=BE又由已知BE=CEBC=2BEAB=2OD所以AB=BC即ABC为等腰三角形，进而得出以点。B、E、D为顶点的四边形是正方形；（3）直接利用三角形的中位线的性质结合菱形的判定方法进而得出答案.【解答】（1）证明：连接ODOE,.O为AB的中点，E为BC的中点， .OE为ABC的中位线， .OE/AC（三角形中位线性质）， /DOEhODA/BOEWA（平行线性质）， .OA=OD/A=ZODA ./DOE=BOE（等量代换）在OD讶口AOBE中'OD=OB,/DOE=/BOE,QE二OE.

25、OD孽OBE（SSS ./ODE=OBE.DE是。O的切线 /ODEhOBE=90.-.OB±BC .BC是。O的切线.（2）解：当/A=ZC=45时，四边形OBDE正方形，证明如下：如图2,连接BD,.AB是。O的直径，BD±AC（直径所对的圆周角为直角），/A=ZB,.AB=BC.D为AC的中点（等腰三角形的性质）， .E为BC的中点， .DE为ABC的中位线， .DE/AB,.DE为。O的切线， ODLDE, ODLAB, ./DOB=OBEWODE=90, .OD=OB，四边形OBE的正方形.故答案为：45°(3)解：CE=BEAACD.DE于OB不平行，

26、以点。B、E、D为顶点的四边形不可能是菱形,故答案为：不可能.18.国家环保局统一规定，空气质量分为5级.当空气污染指数达0-50时为1级，质量为优；51-100时为2级，质量为良；101-200时为3级，轻度污染；201-300时为4级，中度污染；300以上时为5级，重度污染.某城市随机抽取了2015年某些天的空气质量检测结果，并整理绘制成如图两幅不完整的统计图.请根据图中信息，解答下列各题：(1)本次调查共抽取了50天的空气质量检测结果进行统计;(2)补全条形统计图；(3)扇形统计图中3级空气质量所对应的圆心角为72°(4)如果空气污染达到中度污染或者以上，将不适宜进行户外活动，

27、根据目前的统计，请你估计2015年该城市有多少天不适宜开展户外活动.空气质量等级天数统计图空气质量等级天数占所抽取天数百分比统计图【考点】条形统计图；用样本估计总体；扇形统计图.【分析】(1)根据4级的天数数除以4级所占的百分比，可得答案；(2)根据有理数的减法，可得5级的天数，根据5级的天数，可得答案;(3)根据圆周角乘以3级所占的百分比，可得答案；(4)根据样本数据估计总体，可得答案.【解答】解：(1)本次调查共抽取了24+48%=50(天)，故答案为：50;(2) 5级抽取的天数50371024=6天，空气质量等纲天数统计图空气质量等级天数统计图,、10(3) 360X=72SU故答案为

28、：72;(4)365X-X100%=219(天)，0U24+6答：2015年该城市有219天不适宜开展户外活动.19.如图，在平面直角坐标系xOy中，直线y=mx+1与双曲y=(k>0)相交于点A、B,点C在x轴正半轴上，点D(1,-2),连结OAODDCAC四边形AODCJ菱形.(1)求k和m的值；(2)根据图象写出反比例函数的值小于2时x的取值范围；(3)设点P是y轴上一动点，且SaOA=S菱形OACD求点P的坐标.【考点】反比例函数综合题.【分析】(1)由菱形的性质可知AD关于x轴对称，可求得A点坐标，把A点坐标分别代入两函数函数解析式可求得k和m值；(2)由(1)可知A点坐标为(

29、1,2),结合图象可知在A点的下方时，反比例函数的值小于2,可求得x的取值范围；(3)根据菱形的性质可求得C点坐标，可求得菱形面积，设P点坐标为(0,y),根据条件可得到关于y的方程，可求得P点坐标.【解答】解：(1)如图，连接AD交x轴于点E,.D(1,2), .OE=1,ED=2 四边形AODC1菱形， .AE=DE=2EC=OE=1 A(1,2),将A(1,2)代入直线y=mx+1可得m+1=2解得m=1,k将A(1,2)代入反比例函数y二,可求得k=2;(2)二当x=1时，反比例函数的值为2,，当反比例函数图象在A点下方时，对应的函数值小于2,此时x的取值范围为：xv0或x>1;

30、(3)OC=2OE=2AD=2DE=4.-1S菱形oac=工OC?AD=,4Saoa=S菱形OACDSaoa=4,设P点坐标为(0,y),则OP=|y|,1 .X|y|X1=4,即|y|二8,解得y=8或y=-8,.P点坐标为(0,8)或(0,-8).20.如图，小明站在河岸上的E点，看见正对面的河岸边有一点C,此时测得C点的俯角是30。.若小明的眼睛与地面的距离DE是1.6米，BE=1米，BE平行于AC所在的直线，迎水坡的坡度i=4:3,坡长AB=10米，求河宽AC.(结果保留整数，参考数据：斐=1.73)【考点】解直角三角形的应用-仰角俯角问题；解直角三角形的应用-坡度坡角问题.【分析】作

31、BQLAC交CA的延长线于Q,彳EMLAC交CA的延长线于M根据坡度的概念分别求出AQBQ的长，根据矩形的性质求出QMBE的长，得到DM根据正切的定义求出CM结合图形计算即可.【解答】解：作BQLAC交CA的延长线于Q,彳EMLAC交CA的延长线于M,迎水坡的坡度i=4:3,即4P、，.而二百，又AB=10米，.BQ=8米，AQ=6米，四边形BQM段矩形，EM=BQ=8k,QM=BE=1k,.DM=DE+EM=9.6K,八-上一DM“在RtADCM,tan/CF，/C=30,Cjil96CM=an30。=tan30"，.AC=CMAQ-QMk10米,答：？R"宽AC约为10

32、米.21.某批发市场有中招考试文具套装，其中A品牌的批发价是每套20元，B品牌的批发价是每套25元，小王需购买AB两种品牌的文具套装共1000套.(1)若小王按需购买A、B两种品牌文具套装共用22000元，则各购买多少套？(2)凭会员卡在此批发市场购买商品可以获得8折优惠，会员卡费用为500元.若小王购买会员卡并用此卡按需购买1000套文具套装，共用了y元，设A品牌文具套装买了x包，请求出y与x之间的函数关系式.(3)若小王购买会员卡并用此卡按需购买1000套文具套装，共用了20000元，他计划在网店包邮销售这两种文具套装，每套文具套装小王需支付邮费8元，若A品牌每套销售价格比B品牌少5元，请

33、你帮他计算，A品牌的文具套装每套定价不低于多少元时才不亏本(运算结果取整数)？【考点】一次函数的应用.【分析】(1)设小王需购买AB两种品牌文具套装分别为x套、y套，则,x+y=100020H25尸2200。据此求出小王购买AB两种品牌文具套装分别为多少套即可.(2)根据题意，可得y=500+0.8x20x+25,据此求出y与x之间的函数关系式即可.(3)首先求出小王购买AB两种品牌文具套装分别为多少套，然后设A品牌文具套装的售价为z元，则B品牌文具套装的售价为z+5元，所以125z+875(z+5)>20000+8X1000,据此求出A品牌的文具套装每套定价不低于多少元时才不亏本即可.

34、【解答】解：(1)设小王够买A品牌文具x套，够买B品牌文具y套，答：小王够买A品牌文具600套，够买B品牌文具400套.(2)y=500+0.820x+25=500+0.8=500+20000-4x=-4x+20500,，y与x之间的函数关系式是：y=-4x+20500.(3)根据题意，得：-4x+20500=20000,解得：x=125,，小王够买A品牌文具套装为125套、够买B品牌文具套装为875套，设A品牌文具套装的售价为z元，则B品牌文具套装的售价为(z+5)元，由题意得：125z+875(z+5)>20000+8X1000,解得：z>23.625,答：A品牌的文具套装每套

35、定价不低于24元时才不亏本.22.在ABC中，/ACB=90经过点B的直线l(l不与直线AB重合)与直线BC的夹角等于/ABC分别过点C、A做直线l的垂线，垂足分别为点D、E.(1)问题发现CD1若/ABC=30,如图，则近二_/_；CD1/ABC=45,如图，则近=_彳_;<ZABGc90°,说的值有无变化？请仅就图的情形给出证明.(2)拓展探究(3)问题解决CF5若直线CEAB交于点F,而=飞,CD=4请直接写出线段BD的长.【考点】三角形综合题.A【分析】(1)根据直角三角形的性质得到CD三二BC,根据全等三角形的性质得到BC=AE等量代换得到CD=AE,即可得到结论；如

36、图，推出ACB是等腰直角三角形，求得/CBD=45,证彳#B与E重合，根据等腰直角三角形的性质得到EFAE根据矩形的性质得到EF=CD与得到结论；(2)如图，延长AC与直线L交于G,根据等腰三角形的性质得到BA=BG证得CD/AE),r,-口，CDGC1根据相似三角形的性质得到m；ABVoZ(3)当点F在线段AB上时，过C作CG/l交AE于H,交AB于G推出CF6EFB,一一，CFCG5>根据相似三角形的性质得到而不逋二，设CG=5xBE=6x则AB=10x,根据勾股定理，一，口HGAH1得到AE=8x,由(2)得AE=2CD根据相似三角形的性质得到前方区至，于是得到CH=CG+HG=8

37、艮据平行四边形的性质得至ijDE=CH=8求得BD=DE=BE=2如图，当点F在线段BA的延长线上时，过点C作CG/l交AE于点H,交AB于G,同理可得求得结论.【解答】解：（1）:CDLBD,/CDB=90,/DBChABC=30,*CD-BC,rZACB=ZAEB=90"在ABE与ABC中，/BAE=/ABC=30°,AB=BA.ABCABEBC-AE.CD-.-AE,AE-2，如图，./ABC-45ZACB-90, .ACB是等腰直角三角形， /CBD-45, ./ABD-90, .AE，BC, .B与E重合，1 EF=.-AE, .CD±BD,，四边形CD

38、EF勺矩形， .EF=CD1.CD=.-AE,CD1=AE2'故答案为：J,J-riEiCD(2),的值有无变化，AL理由：如图，延长AC与直线L交于G, /ABC4CBG ./ACB=90, /AGBhBAGBA=BG .AE±l,CD1l, .CD/AE, .GCDoGAE空巫上 AEGA2'(3)当点F在线段AB上时，过C作CG/l交AE于H,交AB于G /DBChHCB /DBChCBF,./CBF=/HCB.CG=BG ./ACB=90, ./CAG它CBF=ZHCB廿ACG=90,/ACGhCAG.CG=AG=BG.CG/l,.CF6EFB,.空皿二口FW

39、E.6，设CG=5xBE=6x,则AB=10x./AEB=90,.AE=8x,由（2）得AE=2CQ,.CD=4,.AE=8,x=1,.AB=10,BE=6,CG=5.GH/I,AGHhAABE.HG_AH二1"Bf-AE一2，HG=32 .CH=CG+HG=83 CG/I,CD/AE,二.四边形CDE的平行四边形，.1.DE=CH=3BD=DE=BE=2如图，当点F在线段BA的延长线上时，过点C作CG/I交AE于点H,交AB于G,同理可得CG=5BH=6HG=3，DE=CH=CGHG=ZBD=DE+BE=3综上可得BD=2或8.图圉DB(E)23.如图，在平面直角坐标系xOy中，抛物线y=ax2+"x+c与直线y=-百*-可交于A、B两22点，已知点B的横坐标是4,直线y二-三x-三与x、y轴的交点分别为A、C,点P是抛物(1)求抛物线的解析式；22(2)若点P在直线y一-石x-忑上方，求PAC的最大面积;(3)设M是抛物线对称轴上的一点，以点A、RP、M为顶点的四边形能否成为平行四边形？若能，求出点P的坐标；若不能，请说明理由.【考点】二次函数综合题.22【分析】(1)将x=4代入直线y=