江苏连云港田家炳中学高三数学复习课件同角三角函数的关系

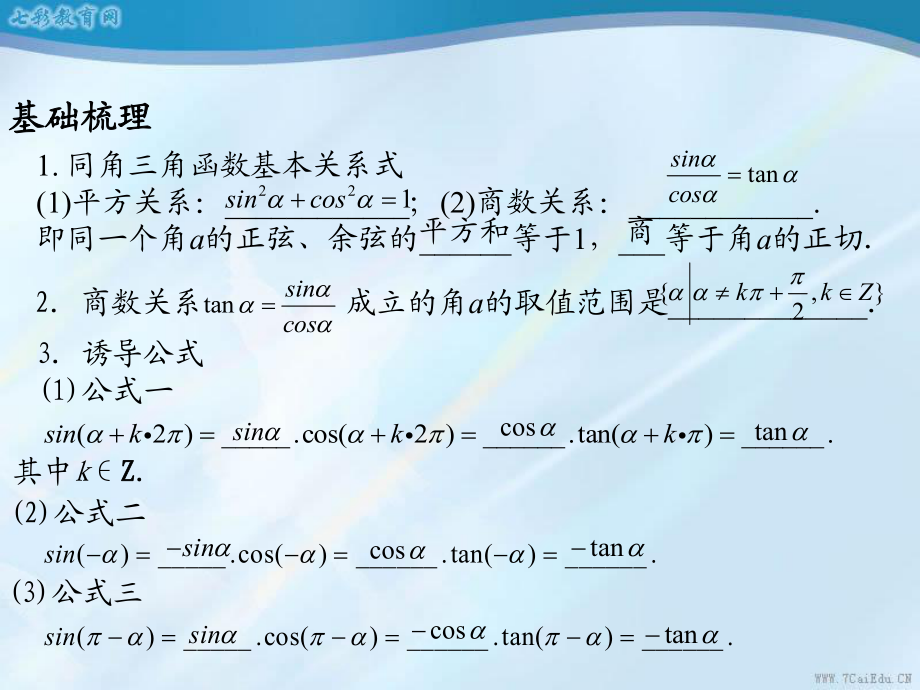
1、第二节第二节同角三角函数的基本关系与诱导公式同角三角函数的基本关系与诱导公式基础梳理基础梳理1. 同角三角函数基本关系式(1)平方关系：_；(2)商数关系：_.即同一个角a的正弦、余弦的_等于1，_等于角a的正切平方和 商 tansincos221sincos成立的角a的取值范围是_ 2. 商数关系 tansincos,2kkZ 3. 诱导公式(1)公式一(2 )_.cos(2 )_.tan()_.sinkkkcossintan其中kZ Z.(2)公式二()_.cos()_.tan()_.sinsincostan(3)公式三()_.cos()_.tan()_.sinsincostan(4)公式

2、四()_.cos()_.tan()_.sinsincostan(5)公式五()_.cos()_.22sin()_.cos()_.22sincossin(6)公式六cossin的正弦(余弦)函数值，分别等于 的_即 的三角函数值，等于 的_函数值，前面加上一个把 看成_时原函数值的符号；2 (),kkZ 同名 锐角 2函数值，前面加上一个把 看成锐角时原函数值的符号余弦(正弦) 4. 必须对一些特殊角的三角函数值熟记，做到“见角知值，见值知角”.不存在不存在角 的弧度数角sincostan030456090120 150 1802700001212121264322356322232321013

3、22210320133133330基础达标基础达标451. 若sin = ，且 是第二象限角，则tan =_.2. 已知sin53.13=a，则cos143.13=_.解析：cos 143.13=cos(90+53.13)=-sin 53.13=-a.解析： 为第二象限角， 21sin2431,55 454.533sincos cos =-=-tan =3. (2011 镇江调研)已知 sin,2m则 cos_.解析： sincos,2mcoscos.m 而 22221 sincos1 sincos,1sincossin cossincos解析： 除以 2,cos则原式= 2217.15tan

4、tantan 5. (必修4P23第15题改编)已知 cos(1),6m m则5cos_.655coscoscos.666m 解析： tan2,4. (必修4P22第9题改编)若 那么 1 sincos_.经典例题经典例题题型一三角函数式的求值【例1】已知 是第三象限角，且 322( ).32sincossinsinfcossincos(1)化简 ；( )f(2)若 31cos,25求 的值 ( )f分析：利用诱导公式及“奇变偶不变，符号看象限”原则对式子进行化简即可解：(1)根据诱导公式 322( )32sincossinsinsin coscossinfcossinsincossincos

5、222.sincoscossincos由同角三角函数关系可知 (2)由 31cos,25则有 1sin,5 而 是第三象限角，2 6cos,5 则 2 6( ).5f 变式1-1(2010全国)记cos(-80)=k，那么tan 100=_.-解析：sin80= 2221801( 80 )1coscosk 所以tan100=-tan80= 2801.80sinkcosk 题型二三角恒等式的证明【例2】求证： 22222112tan.coscossinasin分析：三角恒等式的证明时，常遵循“由繁到简，由多到少”及“切化弦”等证明思路，本题只需要合理利用同角三角函数关系即可解：左边= 22222

6、22222211111coscossinsincossincossinsincossin22222212tan2cossinsincoscos 右边 题型三三角函数在方程中的应用【例3】已知 是关于x的二次方程 sin ,cos22( 21)20 xxm的两根，求 221cossintantan的值 分析：利用根与系数的关系可得出 的值，结合同角三角函数的关系可求出值sin,sincoscos解：由题意有 21,2,sincossin cosm 由 则 221,sincos212 21.28sincosmsin cos 而 2222sin222coscossinsincossin coscos

7、sincoscossincossincos221cossintantan将 212 21sincos,sincos28 代入得 23 252.12cossintantan变式3-1已知 sin ,cos22( 31)20 xxm是方程 的两个根 求：(1)m的值；(2) .11sincoscottan解析：(1)由题意知31,2,sincossin cosm则 213.24sincosmsin cos 2211sincossincoscottansincoscossin(2) 2231.2sincossincossincos题型四三角函数公式在解三角形中的应用【例4】在ABC中，若 sin(2

8、)2sin(). 3cos2cos(),ABAB 求ABC的三个内角值分析：由诱导公式可化简得 sin2sin ,AB3cos2cos ,AB可求出角A，进一步即可求出角B和角C.22sincos1,AA此时A，B均为钝角，不可能 解：由已知得 sin2sin ,AB3cos2cos ,AB222cos1,cos,2AA 两式平方相加，得 若 2cos,2A 则 3cos,2B 即 2cos,2A,4A33coscos,262BAB7().12CAB变式4-1 在锐角ABC中，求证：sinA+sinB+sinCcosA+cosB+cosC.sincos ;sincos ,BCCA解析：ABC是

9、锐角三角形， ,2AB即 0,22ABsinsin(),2AB即 sincos ;AB同理， sinsinsincoscoscos .ABCABC易错警示易错警示 已知1sincos,(0, ),5求tan的值.1sincos,5错解 两边平方得 21(sincos)12sincos,25 可得 242sincos,25 从而 249(sincos)1 2sincos,25 所以 7sincos,5 解得 4,53,5sincos 或 3,54,5sincos 4tan3 或 3tan.4 1sincos,5正解 两边平方得 21(sincos)12sincos,25 可得 242sincos,25