华师大版八年级数学下册知识要点

1、学习必备欢迎下载八年级下数学各章知识要点第17章分式复习要点1、形如AB（A、B都是整式，且B中含有字母，BWO）的式子叫做分式。整式和分式统称有理式。2、分母W0时，分式有意义。分母=0时，分式无意义。3、分式的值为0,要同时满足两个条件：分子=0,而分母4、分式基本性质：分式的分子、分母都乘以或除以同一个不为0的整式，分式的值不变。5、分式、分子、分母的符号，任意改变其中两个的符号，分式的值不变。6、分式四则运算1）分式加减的关键是通分，把异分母的分式，转化为同分母分式，再运算.2）分式乘除时先把分子分母都因式分解，然后再约去相同的因式。3）分式的混合运算，注意运算顺序及符号的变化，4）分

2、式运算的最后结果应化为最简分式或整式.7、分式方程1）分式化简与解分式方程不能混淆.分式化简是包等变形，不能随意去分母.2）解分式方程的步骤：第一、化分式方程为整式方程；第二，解这个整式方程；第三，验根，通过检验去掉增根。3）解有关应用题的步骤和列整式方程解应用题的步骤是一样的：设、歹h解、验、答。第18章函数及图象的复习要点1、规定了原点、正方向和单位长度的直线叫数轴。数轴上的点与实数对应。数轴上的点A、B的坐标为x1、x2,则AB=1。2、具有公共原点且互相垂直的两条数轴就构成平面直角坐标系。坐标平面内的点与有序实数对一一对应。3、坐标轴上的点不属于任何象限。x轴上的点纵坐标y=0;y轴上

3、的点横坐标X=00第一象限内的点x>0,y>0;第二象限内的点x<0,y>0;第三象限内的点x<0,y<0;第四象限内的点x>0,y<0;由此可知，x轴上方的点，纵坐标y>0;x轴下方的点，纵坐标y<0;y轴左边的点，横坐标x<0；y轴右边的点，横坐标x>0.4、关于某坐标轴对称的点，这个轴的坐标不变，另一个轴的坐标互为相反数。关于原点对称的点，纵、横坐标都互为相反数。关于第一、三象限角平分线对称的点，横纵坐标交换位置；关于第二、四象限角平分线上对称的点，不但横纵坐标交换位置，而且还要变成相反数。学习必备欢迎下载5、第一、

4、三象限角平分线上的点，横纵坐标相等；第二、四象限角平分线上的点，横纵坐标互为相反数。6、在一个变化过程中，存在两个变量x、y,对于x的每一个取值，y都有唯一的一个值与之对应，我们就说y是x的函数。x是自变量，y是因变量。函数的表示方法有：解析式法、图象法、列表法。7、函数自变量的取值范围：函数的解析式是整式时，自变量可取全体实数；函数的解析式是分式时，自变量的取值应使分母W0;函数的解析式是二次根式时，自变量的取值应使被开方数>0.函数的解析式是负整指数和零指数时，底数wQ对于反映实际问题的函数关系，应使实际问题有意义.8、如果y=kx+b(k、b是常数，kw0),B么，y叫x的一次函数

5、。如果y=kx(k是常数，k0),那么，y叫x的正比例函数。9、点在函数的图象上的代数意义是：这一点的坐标满足函数的解析式。两个函数有交点的代数意义是：两个函数的解析式组成的方程组的解就是交点的坐标。10、一次函数y=kx+b的性质：(1)一次函数图象是过两点的一条直线，|k|的值越大，图象越靠近于y轴。(2)当k>0时，图象过一、三象限，y随x的增大而增大；从左至右图象是上升的(左低右高)；(3)当k<0时，图象过二、四象限，y随x的增大而减小。从左至右图象是下降的(左高右低)；(4)当b>0时，与y轴的交点(0,b)在正半轴；当b<0时，与y轴的交点(0,b)在负半

6、轴。当b=0时，一次函数就是正比例函数，图象是过原点的一条直线(5)几条直线互相平行时，k值相等而b不相等。11、如果y=kx(k是常数，kw0那么，y叫x的反比例函数。12、反比例函数y=kx的性质：(1)反比例函数的图象是双曲线，图象无限的靠近于x、y轴。(2)当k>0时，图象的两个分支位于一、三象限，在每个象限内，y随x的增大而减小，从左至右图象是下降的(左低右高)；(3)当k<0时，图象的两个分支位于二、四象限，在每个象限内，y随x的增大而增大，从左至右图象是上升的(左高右低)。(4)反比例函数y=kx与正比例函数y=kx的交点关于原点对称。第19章全等三角形1、判断正确或

7、错误的句子叫做命题.正确的命题称为真命题，错误的命题称为假命题.2、命题是由题设、结论两部分组成的.题设是已知事项；结论是由已知事项推出的事项.常可写成如果，那么”的形式.用如果”开始的部分就是题设，而用那么”开始的部分就是结论.3、直角三角形的两个锐角互余.学习必备欢迎下载4、三角形全等的判定：方法1:如果两个三角形有两边及其夹角分别对应相等，那么这两个三角形全等.简记为S.A.S.（或边角边）.方法2:如果两个三角形有两个角及其夹边分别对应相等，那么这两个三角形全等.简记为A.S.A.（或角边角）方法3:如果两个三角形有两个角和其中一个角的对边分别对应相等，那么这两个三角形全等.简记为A.

8、A.S.（或角角边）.方法4:如果两个三角形的三条边分别对应相等，那么这两个三角形全等.简记为S.S.S（或边边边）.方法5（只能用于直角三角形）：如果两个直角三角形的斜边和一条直角边分别对应相等，那么这两个直角三角形全等.简记为H.L.（或斜边、直角边）.5、一般来说，在两个命题中，如果第一个命题的题设是第二个命题的结论，而第一个命题的结论是第二个命题的题设，那么这两个命题叫做互逆命题.如果把其中一个命题叫做原命题，那么另一命题就叫做它的逆命题.6、如果一个定理的逆命题也是定理，那么这两个定理叫做互逆定理，其中的一个定理叫做另一个定理的逆定理.7、如果一个三角形有两个角相等，那么这两个角所对

9、的边也相等.（简写成等角对等边38、如果三角形的一条边的平方等于另外两条边的平方和，那么这个三角形是直角三角形.（勾股定理的逆定理）9、角平分线上的点到这个角的两边的距离相等.到一个角两边的距离相等的点在这个角的平分线上.10、线段的垂直平分线上的点到这条线段的两个端点的距离相等；到一条线段的两个端点的距离相等的点在这条线段的垂直平分线上。第20章平行四边形的判定1、四边形的内角和定理：四边形内角和等于360°2、多边形内角和定理：n边形的内角和等于（n2）X80°3、多边形的外角和定理：任意多边形的外角和等于360°4、n边形对角线条数公式：n（n3）2（n&g

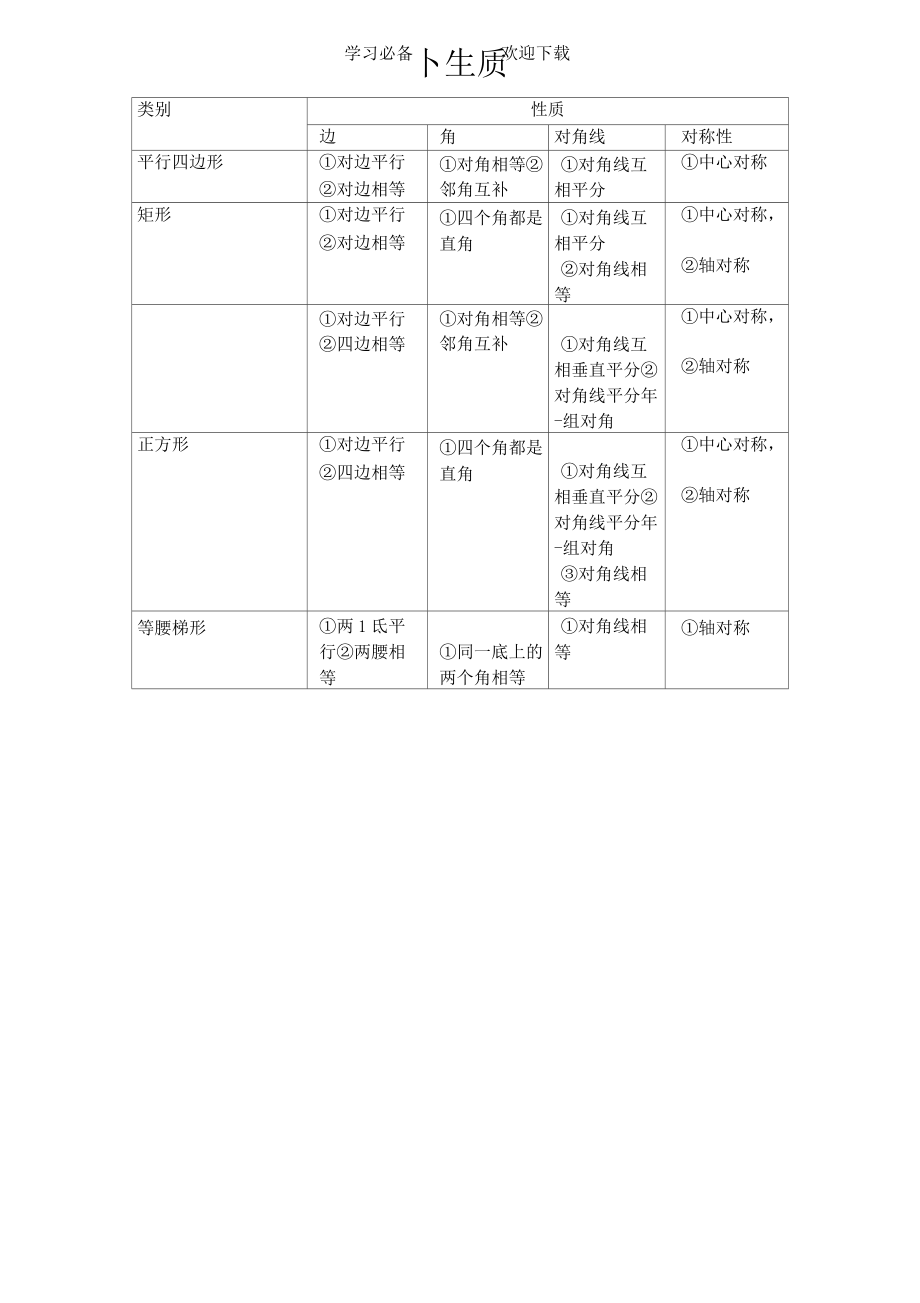
10、t;3）5、中心对称：把一个图形绕某一个点旋转180°,如果它能够与另一个图形重合，那么就说这两个图形关于这个点对称。6、中心对称图形：把一个图形绕某一个点旋转180°,如果它能够和原来的图形互相重合，那么就说这个图形叫做中心对称图形。7、中心对称的性质：关于中心对称的两个图形是全等形；关于中心对称的两个图形，对称点的连线都经过对称中心，并且被对称中心平分。8、平行四边形的性质和判定学习必备欢迎下载卜生质类别性质边角对角线对称性平行四边形对边平行对边相等对角相等邻角互补对角线互相平分中心对称矩形对边平行对边相等四个角都是直角对角线互相平分对角线相等中心对称，轴对称对边平行四

11、边相等对角相等邻角互补对角线互相垂直平分对角线平分年-组对角中心对称，轴对称正方形对边平行四边相等四个角都是直角对角线互相垂直平分对角线平分年-组对角对角线相等中心对称，轴对称等腰梯形两1氐平行两腰相等同一底上的两个角相等对角线相等轴对称学习必备欢迎下载判定类别判定平行四边形两组对边分别分别平行的四边形是平行四边形两组对边分别分别相等的四边形是平行四边形一组对边平行且相等的四边形是平行四边形两组对角分别相等的四边形是平行四边形对角线互相平分的四边形是平行四边形矩形有一个角是直角的平行四边形是矩形有二个角是直角的四边形对角线相等的平行四边形是矩形有一组邻边相等的平行四边形是菱形四条边都相等的四边

12、形是菱形对角线互相垂直的平行四边形是菱形对角线平分每一组对角的四边形是正方形一组邻边相等的矩形是正方形有一个角是直角的菱形是正方形对角线互相垂直且相等的平行四边形是正方形等腰梯形两腰相等的梯形是等腰梯形同一底上的两个角相等的梯形是等腰梯形对角线相等的梯形是等腰梯形第21章数据的整理与初步处理1、平均数=总量旬、份数。数据的平均数只有一个。学习必备欢迎下载一般说来，n个数、的平均数为=1n（x1+x2+xn）一般说来，如果n个数据中，x1出现fl次，x2出现f2次，xk出现fk次，且f1+f2+fk=n则这n个数的平均数可表示为x=x1f1+x2f2+xkfkn。其中fin是xi的权重（i=1,

13、2-k）。加权平均数是分析数据的又一工具。当考虑不同权重时，决策者的结论就有可能随之改变。2、将一组数据按由小到大（或由大到小）的顺序排列（即使有相等的数据也要全部参加排列），如果数据的个数是奇数，那么中位数就是中间的那个数据。如果数据的个数是偶数，那么中位数就是中间的两个数据的平均数。一组数据的中位数只有一个，它可能是这组数据中的一个数据，也可能不是这组数据中的数据.3、一组数据中出现的次数最多的数据就是众数。一组数据可以有不止一个众数，也可以没有众数（当某一组数据中所有数据出现的次数都相同时，这组数据就没有众数）.4、一组数据中的最大值减去最小值就是极差：极差=最大值-最小值2-5、我们通常用S表示一组数据的方差，用X表示一组数据的平均数，X1X2、表示各个原始数据.则S2=1/5（X1-X2+（X1/2（平方单位）求方差的方法：先求平均数，再求偏差，然后求偏差的平方和，最后再