重积分二重积分的计算81435ppt课件

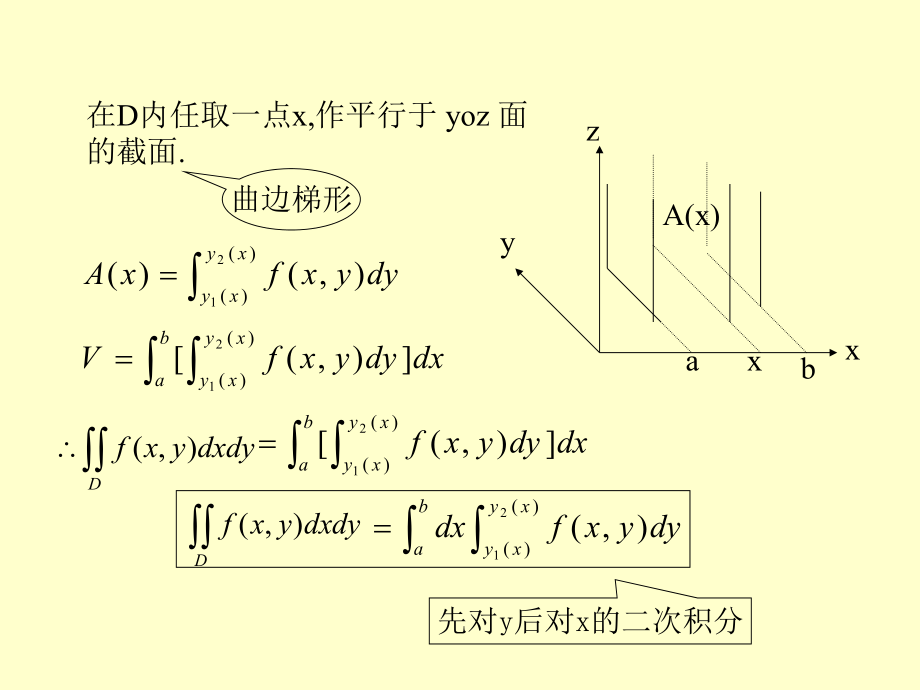
1、第二节第二节 二重积分的计算方法二重积分的计算方法第二节第二节 二重积分的计算方法二重积分的计算方法一一.在直角坐标系中的计算方法在直角坐标系中的计算方法在直角坐标系中,用平行于坐标轴的直线将积分区域D分成n份小矩形,可知:利用几何意义-曲顶柱体的体积研究其计算方法:将曲顶柱体看作已知平行截面面积的立体,利用定积分计算.化成两次定积分dxdydDDdxdyyxfdyxf),(),(1.设),()(,:21xyyxybxaDX型域abD)(1xyy )(2xyy )()(21),()(xyxydyyxfxAabxxyzA(x) baxyxydxdyyxfV),()()(21Ddxdyyxf),(

2、 baxyxydxdyyxf),()()(21Ddxdyyxf),(baxyxydyyxfdx)()(21),(先对y后对x的二次积分在D内任取一点x,作平行于 yoz 面的截面.曲边梯形2.设),()(,:21yxxyxdycDY型域同理可得:Ddxdyyxf),(dcyxyxdxyxfdy)()(21),(先对x 后对y 的二次积分注:(1).如果D 既是X 型域又是Y 型域,那么dcyxyxdxyxfdy)()(21),(baxyxydyyxfdx)()(21),(dydxyxfdcyxyx )()(21),(Ddxdyyxf),(cdD)(1yxx)(2yxx(2).如果D 既不是X

3、型域又不是Y 型域,则用平行于坐标轴的 直线将D 分成若干子域,利用积分的可加性进行计算.选择积分域和积分次序是计算的关键选择积分域和积分次序是计算的关键例如:1D3D2D分块越少越好分块越少越好第一次积分要易于计算第一次积分要易于计算 例1 计算Dydxdyx2xyxyD, 2, 1由 围成.12解一:,1 , 21:xyxDX 型域xDydyxdxydxdyx122122124)22(dxxx152922212yDydxxdyydxdyx214)338(dyyy1529解二:, 2, 21:xyyDY 型域 例2 计算DxydxdyxyxyD2, 2由 围成.2212yyDxydxdyxy

4、dxdy-12解一:, 2, 21:2yxyyDY型域2152)2(21dyyyy845解二:如果选择 X 型域,需要将 D 分成两部分,显然复杂.分块越少越好分块越少越好 例3 计算DdxdyyysinxyxyD2,由 围成.yyDdxyydydxdyyy2sinsin10(1,1)如果先对 y 积分,dyyysin无法进行因此先对 x 积分,10)sin(sindyyyy1sin1第一次积分要易于计算第一次积分要易于计算DxdxdyBAOD.,) 1 , 2()2 , 1 (),0 , 0(. 4求为顶点的三角形区域和是由点设例xyxyxyABOBOA32,2,和的方程相应为和直线解,21

5、两个区域和分成它将轴作垂线向过点DDDAPxA21dddddxdyx DDDyxxyxxxxxxyxxyxx32212210dddd212102d233d23xxxxx.232123|212132103xxx例5.交换积分次序:2202022002),(),().2(xxdyyxfdxdyyxfdxyydxyxfdy222210),(1-220yydxyxfdy),().1 (101xxdxyxfdx2),(10二二.在极坐标系中的计算方法在极坐标系中的计算方法在极坐标系中,设D的边界与过极点的射线相交不多于两点,化成两次定积分rdrddDDrdrdrrfdyxf)sin,cos(),(用过极

6、点的射线和以极点为圆心的圆周将D分成若干子域,如图可知:dr+drrd基本类型:)()(,:21rrrDD)()(21)sin,cos()sin,cos(rrDrdrrrfdrdrdrrf注:(1).只研究先对r后对 的积分次序;(2).如果D是曲边扇形:)(0 ,rr )(0)sin,cos()sin,cos(rDrdrrrfdrdrdrrf)(020)sin,cos()sin,cos(rDrdrrrfdrdrdrrf(3).如果D包含极点:)(0 ,20rr 例6 计算Ddxdyyx)(222222:byxaDbraD,20:baDrdrrddxdyyx22022)(204| )4(drb

7、a)(244ab 例7 计算Dyxdxdye22222:ayxDDyxdxdye22arrdred0202200| )2(2dear)1 (2ae此题若采用直角坐标系方法无法积分注意注意:下列情形适合用极坐标计算下列情形适合用极坐标计算:(1).积分区域适于极坐标表示,例如:圆,圆环;(2).被积函数形如 ;)(22yxf(3).用直角坐标系计算不出时.例8.化为极坐标形式:22020),(yRyRdxyxfdy2R0sin2020)sin,cos(Rrdrrrfd1)(81)(2)()(),(1, 0,),(),(,),(. 12xyDxyCxyBxyAyxfxxyyDdudvvufxyyx

8、fyxfD等于所围区域，则是由其中且连续设难题解析0)()sincos(4)(2)(sincos2)()sincos() 1, 1() 1 , 1(),1 , 1 (. 21111DdxdyyxxyCxydxdyBydxdyxAdxdyyxxyDDxOyDDDDD在第一象限的部分，则是为顶点的三角形区域，和平面上以是设.1, 1,)(1 . 3222上的连续函数是围成的区域，由，其中DfxyxyDdyxyfxDxOy1-111D2D3D4D.52dd2d2d)(dd)(1 0d)(1 ,33434343214321001222222xDDDDDDDDDDDDDyxxxyxxyfxyxyfxyxyfxx为奇函数因为被积函数关于原式解).0()()()( ). 400fafdyyxxayfdxxfxa连续，证明：设).0()(d)( dd)( d221dy)( d)()( dyd)()( d0220sin22220000fafyyftyyfxyaxyayfxyxxayfyyxxayfxaatyayaxayaayaxa解).12(