12.2全等三角形的判定---ASA教学设计

1、课题名称：12.2全等三角形的判定-ASA教师姓名：张慧 学校：北京市平谷区峪口中学教师年龄：31岁 教龄：5年职称：中教二级教学背景分析(1) 本课时教学内容的功能和地位：本节课是研究三角形全等的判定定理之一-角边角定理，它是人教版八年级上册第十二章三角形全等的判定”的第三课时，是在学生学习了认识三角形、图形的全等、全等三角形及其性质，以及探究出另外两个三角形全等的判定定理-边边边和边角边定理基础上进行的。一方面判定三角形全等在初中几何学习中对证明线段和角相等是一个非常重要和有效的 方法；另一方面在能力培养上，无论是逻辑思维能力、推理论证能力，还是分析问题解决问题的能力，都可在全等三角形的教

2、学中得以培养和提高。因此，全等三角形的教学对全章乃至以后的学习都是非常重要的。(2)学生情况分析：学生具备一定的自学能力，思维活跃，对自己动手的活动兴趣很高； 学生已经接触过全等三角形的性质和两种判定三角形全等的方法，学生现在处于逻辑推理论证的初步阶段，从这章开始，学生应该逐步学会逻辑推理，这类题的推理书写对学生来说难度比较大，同时学生在解题过程中，找全等条件是一个难点。(2) 教学准备：幻灯片，自制教具教学目标1、知识与技能：(1)在探究过程中得出角边角定理；(2)熟练掌握角边角定理，能灵活运用角边角定理证明两个三角形全等。2、过程与方法：(1)经历探索三角形全等条件的过程，培养观察分析图形

3、能力、动手能力；(2)在运用定理解决问题过程中，培养逻辑推理能力、概括能力和语言表达能力。3、情感态度与价值观：在探索三角形全等条件的过程中，培养善于思考、积极参与数学学习活动、 勇于探索的钻研精神及作交流的意识。教学重难点分析教学重点：寻找判定三角形全等的条件及应用角边角定理解决问题。教学难点：三角形全等条件的探索过程。教学过程教学环节教师活动学生活动设计意图知识回顾前面我们学了哪些判定三角形全等的方法？思考并回答问题回顾本节课所需知 识点，为探究角边 角定理做好铺垫。一、创设情境，导入新课一个三角形硬纸片不小心撕去一个角，现在要去剪一块新的，如果手上没有测量的仪器，怎么做能保证新剪的纸片形

4、状、大小和原来一样吗？思考谈论动手试试以实际问题自然地 创设了情境，既让 学生感受到数学来 源于生活，又让全 体学生参与到学习新知探究归纳总结%动手画一画 和同桌比较思考并回答理解记忆中来，不仅提高了 学生的动手能力而 且激发了学生学习 兴趣和探索热情。通过学生动手实 践，让其通过直观 感知，使知识更加 形象，易于理解。 让学生在合作学习 中主动探究三角形 全等的条件，培养H/) , ， ? 二、实践探索，总结角边角定理 做一做：画一个三角形，使三角形的两 个角分别为40和60,它们的夹边为 8cm,把你所画的三角形和你同桌所画 的三角形进行比较，它们是否全等？若 全等，你能得出什么结论？/八

5、40八608cm你能在参考前面所学两种判定三角形 全等的定理的基础上，试着用一句话来 概括吗？先有学生试着说一说，最后老师补充总 结判定三角形全等的另一种方法：两角和它们的夹边分别相等的两个三角形全等。（简写为：角边角或ASA）也就是说，三角形的两个角的大小和它 们的夹边的长度确定了，这个三角形的 形状和大小就确定了。几何语言：在AABC和ADEF中-Z A= Z DAB=DE/ B=ABCA DEF（ASA）学生动手能力、分 析和探究问题的能 力、归纳知识的能 力、语言组织和表 达能力。在 ABC和 DEF中/A=/DA AC=DFAABCA DEF(ASA)在 ABC和 DEF中/c=/f

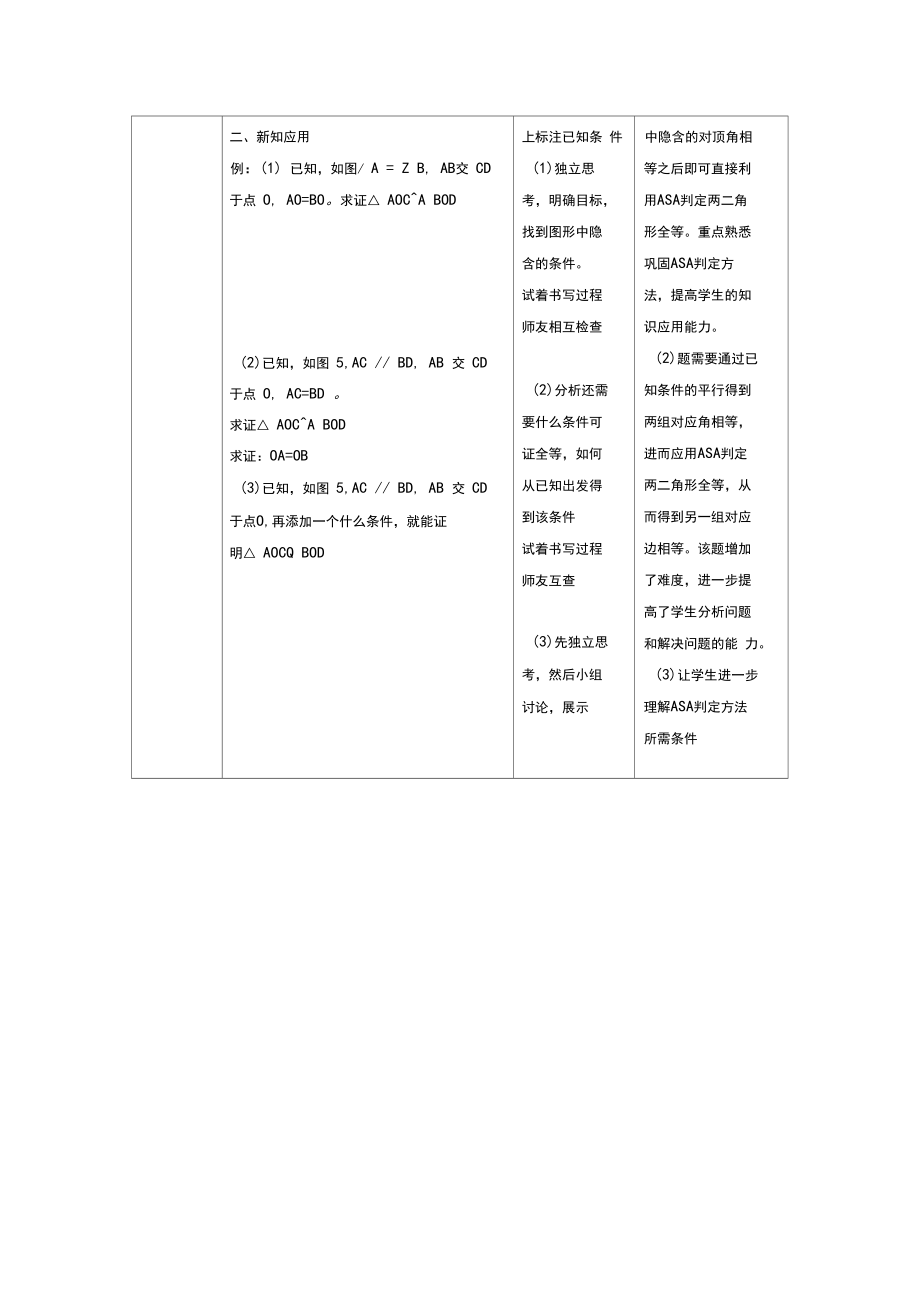
6、1/ B= / E ABCA DEF(ASA)思考并填空，熟悉几何语言的书写读题，在图形让学生体会数学语 言的简洁性，同时 也为下面新知应用 的过程书写打基础巩固利用ASA判定 全等时如何找到全等条件，突破难点本题（1）看出图形二、新知应用例：(1) 已知，如图/ A = Z B, AB交 CD 于点 O, AO=BO。求证 AOCA BOD(2)已知，如图 5,AC / BD, AB 交 CD 于点 O, AC=BD 。求证 AOCA BOD求证：OA=OB(3)已知，如图 5,AC / BD, AB 交 CD 于点O,再添加一个什么条件，就能证明 AOCQ BOD上标注已知条 件(1)独立

7、思 考，明确目标， 找到图形中隐 含的条件。 试着书写过程 师友相互检查(2)分析还需 要什么条件可 证全等，如何 从已知出发得 到该条件 试着书写过程 师友互查(3)先独立思 考，然后小组 讨论，展示中隐含的对顶角相 等之后即可直接利 用ASA判定两二角 形全等。重点熟悉 巩固ASA判定方 法，提高学生的知 识应用能力。(2)题需要通过已 知条件的平行得到 两组对应角相等， 进而应用ASA判定 两二角形全等，从 而得到另一组对应 边相等。该题增加 了难度，进一步提 高了学生分析问题 和解决问题的能 力。(3)让学生进一步 理解ASA判定方法 所需条件巩固练习1、如图应填什么条件就能证明 AO

8、CA BOD?.A =/B(已知)OA -OB(已知)! ()AOC ABOD ()2、已知：如图，在 AABC和4DEF中, 点A、F、C、D四点在同一条直线上， 以下有四个论断：(1) AB=DE ; (2)AF=DC ;(3) /B=/E;(4) AB / DE 请用其中三 个作为条件，余下的一个作为结论，编 一道几何证明题，并写出证明过程。3、如图，要测量河两岸相对的两点A,B的距离，可以在 AB的垂线BF上取 两点C, D ,使BC=CD ,再定出BF的 垂线DE,使A, C, E在一条直线上， 这时测得DE的长就是AB的长，为什 么？独立完成师傅给学友检查独立思考 学友说给师傅 听

9、，师友讨论 各自书写过程通过实物投影 展示不同方 法，及时鼓励 和肯定不同的 做法，激发学 生探索热情。审题，在图中 标注已知条 件，思考 学友把自己思 路说给师傅听 师友讨论 各自书写过程 展示进一步明确ASA的条件，巩固所学知识本题比较灵活，进 一步巩固所学知 识，提高学生分析 问题、解决问题以 及语言表达能力。通过贴近生活的实 际问题，让学生体 会到数学源于生 活，并可以用于解 决生活中的实际问 题，让学生体会到 数学的实用性，激 发学习积极性，提 高解决问题的能 力。拓展提高开拓思维1. (1)已知：如图，/AB=AC , / B = / C。求A(2)如果图形旋转后，&ADAE =

10、/ BAC , 证：AD=AE pzC rB专论是否成立？rZB先独立思考小组讨论开拓学生思维，满 足/、同层次学生学 习的需要，使每个 层次的学生都有收 获和提高。I寸E课堂小结1 .本节课你学到了哪些知识？2 .在学习方法和数学思想方法上有哪些收获？学生总结互相补充培养学生归纳总结能力和语言表达能力课堂检测1、如图，在 ABC和4ADC中，二C21=/2（已知）J ）123=/4（已知） ABCA ADC（）2、如图，已知/ ABC = / DCB , / ACB = / DBC。求证： ABCA DCB。A、. DC BC独立完成检测学生对本节课知识的掌握情况学生活动说明在探索新知的开始

11、阶段，让每个学生都经历动手实践、猜想、 讨论、动手画三角形的过 程，既提高了学生的动手实践能力和合作互助意识，又为学生今后研究这类问题提供了方法和思路，培养了学生数形结合的思想；在将定理转化为数学语言的时候，设计相对开放的空间，帮助学生更好的理解角边角的条件；在例题设计中，让学生经历一图多题，设计开放的结论，逐层深入，拓展学生思维，培养识图能力，激发学习热情。教学设计的说明本节课注重学生主体地位的体现，注重学生动手能力的提高和学生学习兴趣的激发；与此同时通过设计一个个递进的问题，引导学生不断思考、探索，体现了教师的主导作用。本节课注重培养学生观察、 发现和提出问题及归纳总结能力的培养。通过观察图形，自己发现并提出问题， 设计中利用了从“特殊到一般”的认识方法