平面力系的简化和平衡方程

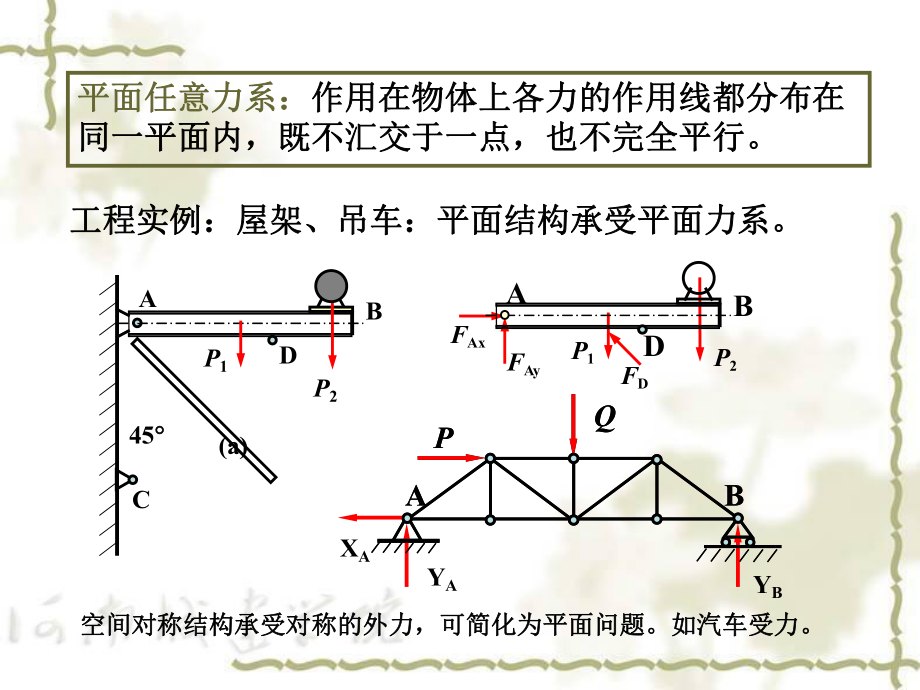
1、Architectural Mechanics4.1 平面任意力系向一点的简化平面任意力系向一点的简化主矢和主矩主矢和主矩4.2 平面平面任意任意力系简化结果的讨论力系简化结果的讨论4.3 平面任意力系的平衡条件平面任意力系的平衡条件平衡方程平衡方程4.4 平面平行力系的平衡方程平面平行力系的平衡方程4.5 物体系的平衡问题物体系的平衡问题4.6 考虑摩擦的平衡问题考虑摩擦的平衡问题平面任意力系：平面任意力系：作用在物体上各力的作用线都分布在作用在物体上各力的作用线都分布在同一平面内，既不汇交于一点，也不完全平行。同一平面内，既不汇交于一点，也不完全平行。工程实例：屋架、吊车：平面结构承受平面

2、力系。工程实例：屋架、吊车：平面结构承受平面力系。P1P2FAxFAyFDDABDCP145 AP2(a)B空间对称结构承受对称的外力，可简化为平面问题。如汽车受力。空间对称结构承受对称的外力，可简化为平面问题。如汽车受力。QPBAXAYAYBQPBAOOO简化中心简化中心Fn mn m3 F3 F2 m2 LOF3 F2 F1 Fn O nFFFF.,321平面任意力系平面任意力系平面汇交力系平面汇交力系 nFFFF.321，平移平移平移平移合成合成 iOiiiFmmFF ，R 力力合成合成OL力偶矩力偶矩合成合成R F1 m1 平面力偶系平面力偶系 nmmmm.,321OR平面任意力系向一

3、点的简化平面任意力系向一点的简化主矢和主主矢和主矩矩 )(iOOFmL主矩的大小：主矩的大小： YYYYRny21 2222)()(YXRRRyx XYarctg XXXXRnx21LOR Oyx指向：由指向：由 Rx、Ry符号定。符号定。与与x方向所夹锐角方向所夹锐角方向方向OL平面任意力系平面任意力系平面汇交力系平面汇交力系R 力力平面力偶系平面力偶系力偶矩力偶矩建立坐标系建立坐标系xy主矢的大小：主矢的大小： iF iFR平面任意力系向一点的简化平面任意力系向一点的简化主矢和主主矢和主矩矩平面任意力系向一点的简化平面任意力系向一点的简化主矢和主主矢和主矩矩简化中心简化中心：O O点称为简

4、化中心。点称为简化中心。主矢主矢R：力系中各力的矢量和；和简化中心的位置：力系中各力的矢量和；和简化中心的位置无关。无关。主矩主矩MO：平面力系中各力对于简化中心的矩的代数：平面力系中各力对于简化中心的矩的代数和称为该力系对简化中心的主矩，其一般随简化中和称为该力系对简化中心的主矩，其一般随简化中心的位置的改变而变化。心的位置的改变而变化。结论：结论：平面任意力系向作用面任一点简化后，一般平面任意力系向作用面任一点简化后，一般得到一个力和一个力偶。这个力的力矢量等于力系得到一个力和一个力偶。这个力的力矢量等于力系中各力的矢量和，即力系的主矢；力偶的矩等于各中各力的矢量和，即力系的主矢；力偶的矩

5、等于各力对简化中心之矩的代数和，即力系对简化中心的力对简化中心之矩的代数和，即力系对简化中心的主矩。主矩。例例 在边长为在边长为a=1m的正方形的四个顶点上，作用有的正方形的四个顶点上，作用有 F1、F2 、 F3 、F4等四个力，如图所示。已知等四个力，如图所示。已知F1=40N，F2=60N，F3=60N，F4=80N。试求该力系向。试求该力系向A A点简化的结果。点简化的结果。F F1 1F F2 2A AyxF F3 360F F4 430解：Rx=40cos45+60cos45+60cos60-80sin30=60.7NRy=40sin45-60sin45-60sin60- 80co

6、s30=-106.1NR=(R x)2+(R y)2=122.4Ncos=60.7/122.4 , =60.27cos= (-106.1/122.3) , =29.9R RMAMA=Mo（Fi）=(-60cos45 -60*cos60 -60sin60 +80sin30 )*1 =-84.4 Nm平面任意力系向一点的简化平面任意力系向一点的简化主矢和主主矢和主矩矩此时，简化结果与简化中心位置无关。此时，简化结果与简化中心位置无关。此时，简化结果与简化中心位置有关。此时，简化结果与简化中心位置有关。0 OL0 R2 2、0 R1 1、0 OL合力偶合力偶原力系原力系力偶系力偶系其合力偶矩其合力偶

7、矩 )(iOOFmL原力系原力系汇交力系汇交力系iFR合力合力R 0 OL0 R2 2、0 OL3 3、0 R0 R1 1、0 OL4 4、0 R0 OL平面任意力系简化结果的讨论平面任意力系简化结果的讨论LOOR RLhO dOO1R即：合力矢等于主矢；合力作用线在简化中心即：合力矢等于主矢；合力作用线在简化中心O O那一侧取决那一侧取决于主矢、主矩方向；合力作用线到于主矢、主矩方向；合力作用线到O O点的距离由点的距离由h h 确定。确定。原力系为平衡力系。原力系为平衡力系。0 OL3、0 R4、0 R0 OL原力系原力系合力合力R力偶等力偶等效表示效表示RLhO R R ROR R O1

8、Rh减去平减去平衡力系衡力系平面任意力系简化结果的讨论平面任意力系简化结果的讨论合力矩定理合力矩定理Rh RmOOL FmO LOOOhRLhO O1hOO1 )(iOOFmLR R为原力系合力为原力系合力RRRRRR R R 平面任意力系的合力对于作用面内任一点的矩等于力系平面任意力系的合力对于作用面内任一点的矩等于力系中所有各力对于该点的矩的代数和。中所有各力对于该点的矩的代数和。平面任意力系简化结果的讨论平面任意力系简化结果的讨论例例 试求合力的大小试求合力的大小, ,方向及作用线到方向及作用线到A A点的距离。点的距离。AB1m1m1m25kN20kN18kN60o30o解解: :主矢

9、主矢Rx= 20cos60o + 18cos30o = 25.59 kNRy= 25+ 20sin60o- 18sin30o = 33.32 kNkNRRRyx01.423 .3259.252222平面任意力系简化结果的讨论平面任意力系简化结果的讨论求力系的主矩求力系的主矩AB1m1m1m25kN20kN18kN60o30oRMA = 125 + 2 20sin60o - 3 18sin30o = 32.64 kNmMAmRMdA777. 001.4264.32Rd048.5201.4259.25arccosarccosRRx平面任意力系简化结果的讨论平面任意力系简化结果的讨论 如果平面任意力

10、系向任一点简化后的主矢和主矩都等于如果平面任意力系向任一点简化后的主矢和主矩都等于零，表明简化后的汇交力系和附加力偶系都自成平衡，则原零，表明简化后的汇交力系和附加力偶系都自成平衡，则原力系必为平衡力系。所以，主矢和主矩都等于零是平面任意力系必为平衡力系。所以，主矢和主矩都等于零是平面任意力系平衡的充分条件。反之，如果主矢和主矩中有一个量不力系平衡的充分条件。反之，如果主矢和主矩中有一个量不为零，则原力系可合成为一个合力或一个力偶；如果主矢和为零，则原力系可合成为一个合力或一个力偶；如果主矢和主矩都不为零，则原力系可进一步合成为一个合力。这种情主矩都不为零，则原力系可进一步合成为一个合力。这种

11、情况下，力系不平衡，所以，主矢和主矩都等于零又是力系平况下，力系不平衡，所以，主矢和主矩都等于零又是力系平衡的必要条件。衡的必要条件。 平面任意力系平衡的充要条件是平面任意力系平衡的充要条件是:力系的主力系的主矢和力系对任一点的主矩都等于零矢和力系对任一点的主矩都等于零。即：。即：0M0FOR平面任意力系平衡的充要条件：平面任意力系平衡的充要条件：0 R0 OL主矢主矢，主矩，主矩即即：0)()(22 YXR0)( iOOFmL所以：所以：平面任意力系平衡的解析条件是平面任意力系平衡的解析条件是：所有各力在两：所有各力在两个个任选任选的坐标轴上的投影的代数和分别等于零，以的坐标轴上的投影的代数

12、和分别等于零，以及各力对于及各力对于任意一点任意一点的矩的代数和也等于零。上式的矩的代数和也等于零。上式称为称为平面任意力系的平衡方程平面任意力系的平衡方程。有独立三个方程，只能求解三个有独立三个方程，只能求解三个未知数这是平面任意力系平衡方未知数这是平面任意力系平衡方程的基本形式程的基本形式 0X 0Y 0FmO 二矩式二矩式：三矩式三矩式：x 轴不得垂直于轴不得垂直于A、B连线。连线。A A、B B、C C三点不共线。三点不共线。 0)(FmB 0X 0)(FmA 0)(FmA 0)(FmC 0)(FmB 三组方程都可用来解决平面任意力系的平衡问题。究竟三组方程都可用来解决平面任意力系的平

13、衡问题。究竟选用哪一组方程，须根据具体条件确定。对于受平面任意力选用哪一组方程，须根据具体条件确定。对于受平面任意力系作用的单个刚体的平衡问题，系作用的单个刚体的平衡问题，只可以写出三个独立的平衡只可以写出三个独立的平衡方程，求解三个未知量。任何第四个方程只是前三个方程的方程，求解三个未知量。任何第四个方程只是前三个方程的线性组合，因而不是独立的。线性组合，因而不是独立的。我们可以利用这个方程来校核我们可以利用这个方程来校核计算的结果。计算的结果。 利用平衡方程，求解平衡问题的步骤为：利用平衡方程，求解平衡问题的步骤为：1 1）选选选取研究对象。应既受已知力，又受要求的力或选取研究对象。应既受

14、已知力，又受要求的力或与要求力相关的力。与要求力相关的力。2 2）画画画受力图。画受力图。 3 3）建建建立坐标系，建立坐标系，原点可任意，使坐标轴与较多的未原点可任意，使坐标轴与较多的未知力平行。知力平行。4 4）列列列平衡方程。列平衡方程。注意：矩心应取在多个未知力作用注意：矩心应取在多个未知力作用线的交点上。线的交点上。5 5）解解解平衡方程。解平衡方程。 6 6）答答答案，必要时作出讨论或说明。答案，必要时作出讨论或说明。 Pdcos45 例例 两根直径为两根直径为d的圆钢，每根重的圆钢，每根重P=2kN，搁置在槽内。，搁置在槽内。忽略接触面的摩擦，求忽略接触面的摩擦，求A、B、C三点

15、的约束力。三点的约束力。O1O2PPAB C45o解：解：3个未知量个未知量NCNBNA 0X 0Y解方程。（略）解方程。（略）研究对象：两根圆钢研究对象：两根圆钢NANC0NB0P0 0)(FM NC dsin45O1xyP ACBPFC45 yx 0X 0Y解得：解得：F FC C28.28kN28.28kN例例 已知如图已知如图ACACCBCBl l，载荷，载荷 P P10kN10kN。设梁和杆的。设梁和杆的自重不计，求铰链自重不计，求铰链A A的约束约束力和杆的约束约束力和杆DCDC所受的力。所受的力。DCFDFCPABD45 解：解：研究对象：研究对象：ABAB梁。梁。 0)(FMA

16、XAFCcos 45 0 YAFCsin 45 P0 FCsin 45lP 2 l0ll由作用反作用公理，由作用反作用公理，CD杆受压力杆受压力 28.28kN XA20kN YA10kN ( (负号表明约束力方向与图示相反负号表明约束力方向与图示相反) )CXAYA 0)(FmC 0X 0)(FmA045cos CAFXlFC 45sinlYA PYA PFC22P PA AB BC CD D4545 y yx xl ll lA AX XA AY YA AF FC CC C4545 P PB BD Dl l如果写出对如果写出对A A、 C C两点的力矩方程和对两点的力矩方程和对x x 轴的投

17、影方程：轴的投影方程：如果写出对如果写出对A A、 D D、 C C三点的力矩方程？思考！三点的力矩方程？思考！lP2 0lP 0 PXA2 例例 水平梁长为水平梁长为4m4m，重，重P P=10kN=10kN，作用在梁的中点，作用在梁的中点C C。承受均。承受均布载荷布载荷q q=6kN/m=6kN/m ，力偶矩，力偶矩m m8kNm8kNm。试求。试求A A、B B处的约束力。处的约束力。P4m2mqmCBA45解：解：研究对象：水平梁研究对象：水平梁ABAB。 0X045cos BARXkNYA12 kNRB14.14 0YAY45sinBR 10 0 0)(FmB4 AY210 0 R

18、B8kNXA20 解得：解得：2q32q 平面平行力系：平面平行力系：各力的作用线相互平行的平面力系各力的作用线相互平行的平面力系 。若取若取y轴与诸力作用线平行，必恒有轴与诸力作用线平行，必恒有 0X0)(0FmYo或或0)(0)(FmFmBA平面平行力系有平面平行力系有2个独立的平衡方个独立的平衡方程，可以求解程，可以求解2个未知数。个未知数。ABAB连线不能平行于各力作用线。连线不能平行于各力作用线。平面平行力系的平衡方程平面平行力系的平衡方程xy 例例 已知已知F=40KN，M=150KNm。求支座。求支座A A、B B处的反力。处的反力。ABFM解：解：研究对象：研究对象：AB梁梁.

19、 . 画受力图画受力图. .6m3mABFMFBFA MA=0 -M +FB 6 - F 9=0FB= =85KN MB=0 - FA 6 - M - F3=0FA= = - 45KN 物体系统物体系统是指由若干个物体通过适当的约束是指由若干个物体通过适当的约束相互连接而组成的系统相互连接而组成的系统. .PACBQQBqEDCA 讨论物体系统平衡时，不仅要考虑系统的讨论物体系统平衡时，不仅要考虑系统的外力外力，还，还要考虑系统内部各物体之间的相互作用力（要考虑系统内部各物体之间的相互作用力（内力内力）。）。解静定物体系统平衡问题的一般步骤解静定物体系统平衡问题的一般步骤: :1)1)分析系统

20、由几个物体组成；分析系统由几个物体组成；2)2)按照便于求解的原则按照便于求解的原则, ,适当选取整体或个体为适当选取整体或个体为研究对象进行受力分析并画受力图；研究对象进行受力分析并画受力图；3)3)列平衡方程并解出未知量。列平衡方程并解出未知量。* *. .一般需取多次研究对象；受力图正确；定路径。一般需取多次研究对象；受力图正确；定路径。 根据求解的问题，恰当的选取研究对象：要使所取物体根据求解的问题，恰当的选取研究对象：要使所取物体上既包含已知条件，又包含待求的未知量。上既包含已知条件，又包含待求的未知量。对选取的研究对象进行受力分析，正确地画出受力图。对选取的研究对象进行受力分析，正

21、确地画出受力图。建立平衡方程式，求解未知量：建立平衡方程式，求解未知量：a)a)根据所研究的力系选择平衡方程式的类别（如汇交力系、根据所研究的力系选择平衡方程式的类别（如汇交力系、平行力系、任意力系等）和形式（如基本式、二矩式、三平行力系、任意力系等）和形式（如基本式、二矩式、三矩式等等）。矩式等等）。b)b)建立投影方程时，投影轴的选取原则上是任意的，并非建立投影方程时，投影轴的选取原则上是任意的，并非一定取水平或铅垂方向，应根据具体问题从解题方便入手一定取水平或铅垂方向，应根据具体问题从解题方便入手去考虑。去考虑。c)c)建立力矩方程时，矩心的选取也应从解题方便的角度加建立力矩方程时，矩心

22、的选取也应从解题方便的角度加以考虑。以考虑。d)d)求解未知量。求解未知量。 静定与超静定问题静定与超静定问题 对每一种力系而言对每一种力系而言, ,若未知量的数目等于独立若未知量的数目等于独立平衡方程的数目平衡方程的数目. .则应用刚体静力学的理论则应用刚体静力学的理论, ,就可就可以求得全部未知量以求得全部未知量, ,这样的问题称为这样的问题称为静定问题静定问题。 若未知量的数目超过独立平衡方程的数目若未知量的数目超过独立平衡方程的数目. .则则单独应用刚体静力学的理论单独应用刚体静力学的理论, ,就不能求出全部未知就不能求出全部未知量量, ,这样的问题称为这样的问题称为静不定问题静不定问

23、题。 静定问题静定问题超静定问题超静定问题 CB三角拱由三角拱由两部分两部分组成，可列出组成，可列出6 6个独个独立的平衡方程，是静定结构，可解。立的平衡方程，是静定结构，可解。例例 已知三角拱的重力及载荷和几何尺寸，求已知三角拱的重力及载荷和几何尺寸，求 A A、B B 的约束力的约束力。QXBYBXCYCXAYAPACBQQXBXAYYB研究对象的选取方案：研究对象的选取方案：（1 1）ACAC和和BC BC （2 2）整体和）整体和BC BC （3 3）整体和）整体和AC AC 分析受力分析受力ACPQYCXC XBXAYAYB解一解一（1 1）研究对象：整体）研究对象：整体 0)(Fm

24、B 0X 0)(FmAYBYA 10BAXX（2 2）研究对象：）研究对象：BCBC 0)(FmCXB代入（代入（1 1）式，可解得）式，可解得X XA A。XCBXBYBCYCQPACBQQ PACBQQ（1）研究对象：）研究对象：AC（2）研究对象：）研究对象：BC 0)(CFm 0X 0)(FmA方程含方程含XC、YC方程含方程含XA、YA方程含方程含XA、XC 0)(CFm 0X 0)(BFm方程含方程含XC、YC方程含方程含XB、YB方程含方程含XB、XCPQACYCXCXAYAXCBXBYBCYCQ6 6个方程、个方程、6 6个未个未知力，联立可解知力，联立可解解二解二 0422

25、CAYqmm解解： 0)(FmB 0)(FmCYC=0.5kN 0)(FmA 0YmA=-4kNmYA=3.5kN 0XXA=0例例 已知已知m=10kNm，q=2kN/m，求，求A、B、C三处的约束力。三处的约束力。qCAB1mm1m1m1mCBABmqqYXAmAYCYCYBXBYBXBYXAmA全面进行受力分全面进行受力分析，选取合适的析，选取合适的研究对象研究对象 0XXB=01 1）研究对象：）研究对象：BCBC05 . 012 qYC025 . 11 BYqYB=1.5kN2 2）研究对象：整体）研究对象：整体02 qYYCA 例例三铰拱三铰拱ABCABC的支承及荷载情况如图所示的

26、支承及荷载情况如图所示. .已知已知P P =20kN, =20kN,均布荷载均布荷载q q = 4kN/m. = 4kN/m.求铰链支座求铰链支座A和和B的约束反力的约束反力. .1m2m2m3mABCqPXAYAXBYB1 1）研究对象：整体）研究对象：整体解解：mA(Fi) = 0- 431.5-203+ 4 YB = 0YB = 19.5 kNYi = 0YA - 20 + 19.5 = 0YA = 0.5 kN 2 2）研究对象：）研究对象： BCXCYC1m3mBCPXBYBmC(Fi) = 0-120 + 219.5 + 3 XB = 0XB = - 6.33 kNXA = -

27、5.67 kNXi = 043+XA+XB = 0整体分析：整体分析： 摩擦是自然界最普遍的一种现象，绝对光滑而没有摩摩擦是自然界最普遍的一种现象，绝对光滑而没有摩擦的情形是不存在的。不过在许多问题中，摩擦对所研究擦的情形是不存在的。不过在许多问题中，摩擦对所研究的问题是次要因素，可以略去不计，但对于另外一些实际的问题是次要因素，可以略去不计，但对于另外一些实际问题，摩擦却是重要的甚至是决定性的因素，必须加以考问题，摩擦却是重要的甚至是决定性的因素，必须加以考虑。例如，重力坝依靠摩擦防止在水压力作用下可能产生虑。例如，重力坝依靠摩擦防止在水压力作用下可能产生的滑动；带轮和摩擦轮的传动等。另外一

28、方面摩擦阻力会的滑动；带轮和摩擦轮的传动等。另外一方面摩擦阻力会消耗能量，产生热、噪声、振动、磨损，特别是在高速运消耗能量，产生热、噪声、振动、磨损，特别是在高速运转的机械中，摩擦往往表现得更为突出。转的机械中，摩擦往往表现得更为突出。 两个相互接触的物体产生相对运动或具有相对运动两个相互接触的物体产生相对运动或具有相对运动的趋势时，彼此在接触部位会产生一种阻碍对方相对运的趋势时，彼此在接触部位会产生一种阻碍对方相对运动的作用。这种现象称为动的作用。这种现象称为摩擦摩擦，这种阻碍作用，称为，这种阻碍作用，称为摩摩擦阻力擦阻力。 摩擦应用摩擦应用 摩擦摩擦滑动摩擦滑动摩擦滚动摩擦滚动摩擦静滑动摩

29、擦静滑动摩擦动滑动摩擦动滑动摩擦静滚动摩擦静滚动摩擦动滚动摩擦动滚动摩擦摩擦摩擦干摩擦干摩擦湿摩擦湿摩擦滑动趋势滑动趋势滑动滑动滚动趋势滚动趋势滚动滚动接触面间无润滑介质接触面间无润滑介质接触面间有润滑介质接触面间有润滑介质 1、静滑动摩擦力、静滑动摩擦力1 1）静滑动摩擦定律）静滑动摩擦定律APQ 重量为重量为P的物体放在粗糙的固定水的物体放在粗糙的固定水平面上平面上, ,受到一个水平拉力受到一个水平拉力Q的作用。的作用。当力当力Q增加到某个数值增加到某个数值QK时时, ,物体处于物体处于将动未动的临界状态。此时静摩擦力达将动未动的临界状态。此时静摩擦力达到最大值到最大值F Fm m , ,

30、称为称为最大静摩擦力最大静摩擦力。APQFNFs当当KQQ 0时时 Xi = 0Q - Fs = 0F s= Q 静摩擦力静摩擦力的大小由平衡条件确定的大小由平衡条件确定, ,并介于零和最大静摩擦力之间并介于零和最大静摩擦力之间, ,方向方向与物体相对滑动趋势的方向相反。与物体相对滑动趋势的方向相反。f fs s静摩擦系数无量纲静摩擦系数无量纲NssFfFmax 2 2）动滑动摩擦定律）动滑动摩擦定律 f 动滑动摩擦因数动滑动摩擦因数，它无量纲，与，它无量纲，与接触物体材料和表面情况有关。动摩接触物体材料和表面情况有关。动摩擦力与静摩擦力不同，没有变化范围。擦力与静摩擦力不同，没有变化范围。通

31、常动摩擦系数小于静摩擦系数。通常动摩擦系数小于静摩擦系数。dFvNF 动摩擦力动摩擦力的大小与接触物体间的正压力成正比，方向的大小与接触物体间的正压力成正比，方向沿接触处的公切线，与相对滑动趋势反向。沿接触处的公切线，与相对滑动趋势反向。NdFfFsff 实际上实际上动摩擦系数动摩擦系数还与接触物体间相对滑动的速度大还与接触物体间相对滑动的速度大小有关，不同材料物体，动摩擦系数随相对滑动速度变化小有关，不同材料物体，动摩擦系数随相对滑动速度变化规律也不同，当滑动速度不大时，动摩擦系数可近似认为规律也不同，当滑动速度不大时，动摩擦系数可近似认为是个常数。是个常数。 2、摩擦角与自锁现象、摩擦角与

32、自锁现象1 1）摩擦角）摩擦角NRFFFNFFtan2N2RFFFNmaxRFFFsmaxftanNmaxmaxFFtanNsmaxFfFmax称为称为摩擦角摩擦角 （angle of friction）RFF NFmaxFmax RFNF 物体处于临界物体处于临界平衡状态时，全约平衡状态时，全约束反力和法线间的束反力和法线间的夹角称为夹角称为摩擦角摩擦角。FN 正压力正压力F 静摩擦力静摩擦力FR 全约束反力全约束反力 （全反力）（全反力） 全反力与接全反力与接 触面法线的夹角触面法线的夹角 max （不滑动的条件）（不滑动的条件）max RF P自锁：自锁：当主动力合力当主动力合力的作用线

33、在的作用线在角内，无角内，无论主动力论主动力Q多大，都能多大，都能使物体保持平衡，这种使物体保持平衡，这种现象称为现象称为自锁自锁。摩擦锥：摩擦锥：如果物体与支承面的静摩擦系如果物体与支承面的静摩擦系数在各个方向都相同，则摩擦角范围在数在各个方向都相同，则摩擦角范围在空间就形成为一个锥体，称为空间就形成为一个锥体，称为摩擦锥摩擦锥。mFQF FR R2 2）自锁现象）自锁现象自锁条件自锁条件 斜面自锁条件斜面自锁条件f螺纹自锁条件螺纹自锁条件f 3、考虑摩擦时物体平衡问题的求解、考虑摩擦时物体平衡问题的求解仍为平衡问题，平衡方程照用，求解步骤与前面基本相同。仍为平衡问题，平衡方程照用，求解步骤与前面基本相同。几几 个个 新新 特特 点点1） 画受力图时，必须考虑摩擦力；画受力图时，必须考虑摩擦力；2） 严格区分物体处于临界、非临界状态；严格区分物体处于临界、非临界状态；3）因）因0FsFmax ，问题的解有时在一个范围