运筹学目标规划

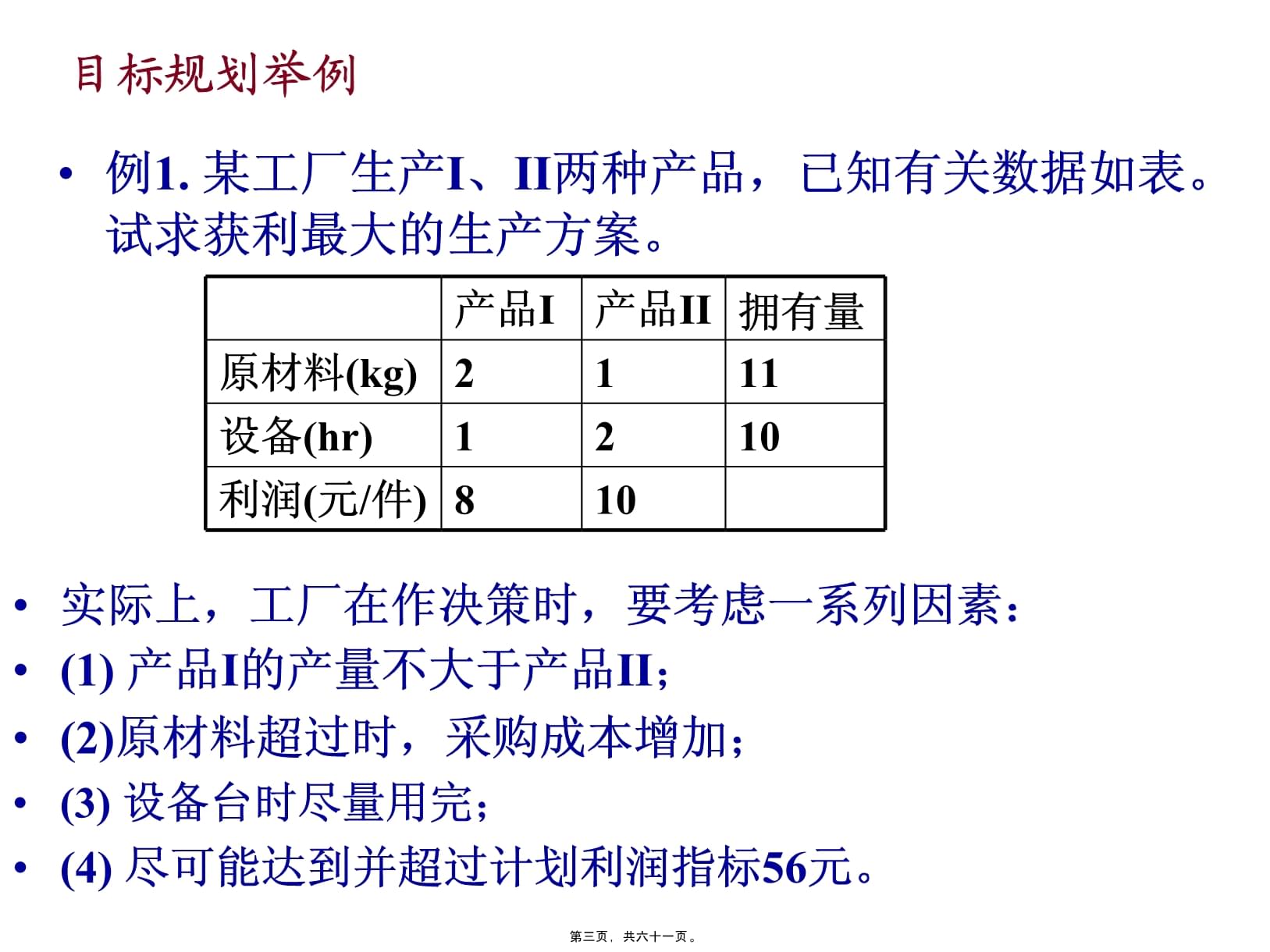
第5章目标规划(Goalprogramming)第1节目标规划的数学模型第2节目标规划的图解法第3节目标规划的单纯形法第一页，共六十一页。

目标规划是在线性规划的基础上，为适应经济管理中多目标决策的需要而逐步发展起来的一个分支。线性规划只研究在满足一定条件下，单一目标函数取得最优解，在实际问题中，可能会同时考虑几个方面都达到最优：产量最高，成本最低，质量最好，利润最大，环境达标，运输满足等。目标规划能更好地兼顾统筹处理多种目标的关系，求得更切合实际要求的解。第1节目标规划的数学模型一、目标规划概述第二页，共六十一页。目标规划举例例1.某工厂生产I、II两种产品，已知有关数据如表。试求获利最大的生产方案。产品I产品II拥有量原材料(kg)2111设备(hr)1210利润(元/件)810实际上，工厂在作决策时，要考虑一系列因素：(1)产品I的产量不大于产品II；(2)原材料超过时，采购成本增加；(3)设备台时尽量用完；(4)尽可能达到并超过计划利润指标56元。第三页，共六十一页。1)线性规划只讨论一个线性目标函数在一组线性约束条件下的极值问题；而目标规划是多个目标决策，可求得更切合实际的解。2)线性规划求最优解；目标规划是找到一个满意解。（一）、目标规划与线性规划的比较4)线性规划的最优解是绝对意义下的最优，但需花去大量的人力、物力、财力才能得到；实际过程中，只求得满意解，就能满足需要（或更能满足需要）。3)线性规划中的约束条件是同等重要的，是硬约束；而目标规划中有轻重缓急和主次之分，即有优先权。第四页，共六十一页。（二）、目标规划的基本概念例1.某工厂生产I、II两种产品，已知有关数据如表。试求获利最大的生产方案。产品I产品II拥有量原材料(kg)2111设备(hr)1210利润(元/件)810实际上，工厂在作决策时，要考虑一系列因素：(1)产品I的产量不大于产品II；(2)原材料超过时，采购成本增加；(3)设备台时充分用完，不加班；(4)尽可能达到并超过计划利润指标56元。x1≤x2，即x1-x2≤0；2x1+x2≤11；x1+2x2=10；8x1+10x2≥56；第五页，共六十一页。目标规划通过引入目标值g和偏差变量d，可以将目标函数转化为目标约束。目标值gk：是指预先给定的某个目标的一个期望值。实现值或决策值fk(xj)：是指当决策变量xj

选定以后，目标函数的对应值。偏差变量（事先无法确定的未知数）：是指实现值和目标值之间的差异，记为d。

单词deviation的首字母。正偏差变量，记为d+：表示实现值超过目标值的部分。负偏差变量，记为d-：表示实现值未达到目标值的部分。1、决策变量xj和正、负偏差变量d+，d-在一次决策中，实现值不可能既超过目标值又未达到目标值，故有d＋×d－＝0，并规定d＋≥0，d－≥0第六页，共六十一页。绝对约束（系统约束）是指必须严格满足的等式或不等式约束。如线性规划中的所有约束条件都是绝对约束，否则无可行解。所以，绝对约束是硬约束。

引入目标值g、正偏差变量d+、负偏差变量d-后，就对某一问题有了新的限制，即目标约束。目标约束既可对原目标函数起作用，也可对原约束起作用。目标约束是目标规划中特有的，是软约束。2、目标约束和绝对约束一般表示为：f(xj)=g+d+-d-第七页，共六十一页。思考：下列三种情形下，如何才算达到目标？若决策目标中规定f(xj)g，则

目标中d+=0；若决策目标中规定f(xj)g，则

目标中d-=0；若决策目标中规定f(xj)=g，则

目标中d+=d-=0.第八页，共六十一页。

准则函数是一个使总偏差量为最小的目标函数，记为minz=f(d＋,d-)。对应一个目标约束，有以下三种情况，但只能出现其中之一：⑴.恰好达到规定的目标值，即f(xj)=g，正、负偏差变量d＋、d-都要尽可能小，则minz=f(d＋＋d-)。⑵.不超过目标值，即f(xj)g

，正偏差变量d＋尽可能小，则minz=f(d＋)。⑶.超过目标值，即f(xj)g

，负偏差变量d-尽可能小，则minz=f(d-)。3、准则函数（即目标规划中的目标函数）第九页，共六十一页。为了将不同级别的目标的重要性用数量表示，引进P1,P2,….，用它表示一级目标，二级目标，….的重要程度，规定P1>>P2>>P3>>…，称P1，P2，….,为级别系数。优先因子Pk是将决策目标按其重要程度排序并表示出来。P1>>P2>>…>>Pk>>Pk+1，k=1,2,…,K。例如，四个决策目标用四个优先因子排序的准则函数：

权系数ωk区别具有同一个优先因子的两个目标的差别的情况。例如，目标i和目标j具有相同的优先因子Pk准则函数：4、优先因子(优先等级)Pk与优先权系数ωk

第十页，共六十一页。对于这种解来说，前面的目标可以保证实现或部分实现，而后面的目标就不一定能保证实现或部分实现，有些可能就不能实现。5、满意解（具有层次意义的解）第十一页，共六十一页。例1.产品I产品II拥有量原材料(kg)2111设备(hr)1210利润(元/件)810(1)产品I的产量不大于产品II；(2)原材料超过时，采购成本增加；(3)设备台时充分用完，不加班；(4)尽可能达到并超过计划利润指标56元。x1≤x2，即x1-x2≤0；2x1+x2≤11；x1+2x2=10；8x1+10x2≥56；引入优先因子P1：x1-x2≤0

；P2：2x1+x2≤11

；P3：x1+2x2=10

；P4：8x1+10x2≥56

；目标约束：

x1-x2=0+d1+-d1-

；

2x1+x2=11+d2+-d2-

；

x1+2x2=10+d3+-d3-

；

8x1+10x2=56+d4+-d4-

；第十二页，共六十一页。例1.产品I产品II拥有量原材料(kg)2111设备(hr)1210利润(元/件)810(1)产品I的产量不大于产品II；(2)原材料超过时，采购成本增加；(3)设备台时尽量用完；(4)尽可能达到并超过计划利润指标56元。x1≤x2，即x1-x2≤0；2x1+x2≤11；x1+2x2=10；8x1+10x2≥56；目标函数minP1d1+

；minP2d2+

；minP3(d3++d3-)；minP4d4-

；minz=P1d1++P2d2++P3(d3++d3-)+P4d4-

目标约束：

x1-x2=0+d1+-d1-

；

2x1+x2=11+d2+-d2-

；

x1+2x2=10+d3+-d3-

；

8x1+10x2=56+d4+-d4-

；第十三页，共六十一页。

例a.某厂计划在下一个生产周期内生产甲、乙两种产品，已知资料如表所示。试制定生产计划，使获得的利润最大？同时，根据市场预测，甲的销路不是太好，应尽可能少生产；乙的销路较好，可以扩大生产。试建立此问题的目标规划模型。12070单件利润3000103设备台时200054煤炭360049钢材资源限制乙甲单位产品资源消耗若在例a中提出下列要求：(1)首先完成或超额完成利润指标50000元；(2)其次，产品甲不超过200件，产品乙不低于250件；(3)再次，现有钢材3600吨必须用完。第十四页，共六十一页。若在例a中提出下列要求：(1)首先，完成或超额完成利润指标50000元；(2)其次，产品甲不超过200件，产品乙不低于250件；(3)再次，现有钢材3600吨必须用完。试建立目标规划模型。分析：本例引入3个优先因子P1,P2,P3；分析：题目有三个目标层次，包含四个目标值。第一目标：第二目标：有两个要求即甲，乙，但两个具有相同的优先因子P2，因此需要确定权系数。本题可用单件利润比作为权系数即70:120，化简为7:12。第三目标：第十五页，共六十一页。目标规划模型为：12070利润3000103台时200054煤炭360049钢材资源乙甲

第十六页，共六十一页。某厂生产Ⅰ、Ⅱ两种产品，有关数据如表所示。试求获利最大的生产方案？ⅠⅡ拥有量原材料2111设备(台时)1210单件利润810在此基础上考虑：(1)产品Ⅱ的产量不低于产品Ⅰ的产量；(2)充分利用设备有效台时，不加班；(3)利润不小于56元。解:分析第一目标：minz1=第二目标：minz2=例2：第三目标：minz3=x1≤x2，即x1-x2≤0；x1+2x2=10；8x1+10x2≥56；第十七页，共六十一页。规划模型：第十八页，共六十一页。（一）、模型的一般形式二、目标规划的数学模型其中，gk为目标约束的目标值；bi为绝对约束的资源值。约束目标函数目标约束资源约束第十九页，共六十一页。（二）、建模的步骤1、根据要研究的问题所提出的各目标与条件，确定目标值，列出目标约束与绝对约束；4、对同一优先等级中的各偏差变量，若需要可按其重要程度的不同，赋予相应的权系数。3、给各目标赋予相应的优先因子Pl

(l=1,2,…,L)。2、可根据决策者的需要，将某些或全部绝对约束转化为目标约束。这时只需要给绝对约束加上负偏差变量和减去正偏差变量即可。第二十页，共六十一页。5、根据决策者的要求，按下列情况之一

构造一个由优先因子和权系数相对应的偏差变量组成的，要求实现极小化的目标函数，即准则函数。⑴.恰好达到目标值，取。⑵.允许超过目标值，取。⑶.不允许超过目标值，取。第二十一页，共六十一页。练习1：1.已知条件如表所示工序型号每周最大加工能力ABⅠ（小时/台）Ⅱ（小时/台）436215070利润（元/台）300450如果工厂经营目标的期望值和优先等级如下：P1:每周总利润不得低于10000元；P2:因合同要求，A型机每周至少生产10台，B型机每周至少生产15台；P3:希望工序Ⅰ的每周生产时间正好为150小时，工序Ⅱ的生产时间最好用足，甚至可适当加班。试建立这个问题的目标规划模型。

第二十二页，共六十一页。第二十三页，共六十一页。练习2、已知一个生产计划的线性规划模型为其中目标函数为总利润，x1,x2为产品A、B产量。现有下列目标：1、要求总利润必须超过2500元；2、由于甲资源供应比较紧张，不要超过现有量140；3、考虑产品受市场影响，为避免积压，A、B的生产量不超过60件和100件。试建立目标规划模型。第二十四页，共六十一页。解：以产品A、B的单件利润比2.5：1为权系数，模型如下：第二十五页，共六十一页。（三）、小结线性规划LP目标规划GP目标函数min,max系数可正负min,偏差变量系数≥0变量xi,xsxa

xixsxad约束条件系统约束（绝对约束）目标约束系统约束解最优最满意建立目标规划的数学模型时，需要确定目标值gk、优先因子Pl、权系数ωj等，它都具有一定的主观性和模糊性，可以用专家评定法给以量化。第二十六页，共六十一页。图解法同样适用两个变量的目标规划问题，但其操作简单，原理一目了然。同时，也有助于理解一般目标规划的求解原理和过程。图解法解题步骤如下：(1)确定各约束条件的可行域，即将所有约束条件（包括目标约束和绝对约束，暂不考虑正负偏差变量）在坐标平面上表示出来；(2)在目标约束所代表的边界线上，用箭头标出正、负偏差变量值增大的方向；第2节目标规划的图解法第二十七页，共六十一页。(3)求满足最高优先等级目标的解；(4)转到下一个优先等级的目标，在不破坏所有较高优先等级目标的前提下，求出该优先等级目标的解；(5)重复4，直到所有优先等级的目标都已审查完毕为止；(6)确定最优解和满意解。例2：用图解法求解目标规划问题。第二十八页，共六十一页。⑴⑵⑶⑷GD结论：有无穷多满意解，G(2,4)～D(10/3,10/3)x2x1用图解法求解例2的目标规划第二十九页，共六十一页。012345678123456⑴⑵⑶Ax2

x1BCB(0.6250,4.6875)~C(0,5.2083)，B、C线段上的所有点均是该问题的解（无穷多满意解）。例b.用图解法求解目标规划问题第三十页，共六十一页。在例2的图解法求解时，把绝对约束作最高级考虑。在例2中依先后次序都能满足d1+=0、d2++d2-=0、d3-=0，因而z*=0。在例b中d1++d1-=0、d2-=0，因而z*=0。但在大多数问题中并非如此，会出现某些约束得不到满足，仅仅得到满意解。第三十一页，共六十一页。例3.彩色电视机黑白电视机拥有量装配线台时1140获利(元/台)8040销量(台)2430该厂目标为：P1：充分利用装配线每周开动超过40小时；P2：加班时间每周尽量不超过10小时；P3：彩色、黑白电视销量尽量超过24、30台。同优先因子下两个目标的权系数可用单件利润比作为权系数即80:40，化简为2:1。设x1，x2分别表示彩色和黑白电视机的产量。第三十二页，共六十一页。以上问题的目标规划模型10203040501020304050x2x1(1)(2)(3)(4)EFBAABEF区域中无法满足d4-=0，只能取一点使d4-尽可能小，即E点。E点为满意解，其坐标(24,26)。第三十三页，共六十一页。

作业：

P127，T5.2（2）练习：

P127，T5.2（1）

第三十四页，共六十一页。Cj

c1c2cn+2mCBXBb

x1x2xn+2m

cj1xj1bo1e11e12e1n+2mcj2xj2bo2e21e22e2n+2mcjmxjm

bomem1em2emn+2mσkjP1α1σ11σ12σ1n+2mP2

α2σ21σ22σ2n+2mPK

αK

σm1σm2σmn+2m第3节目标规划的单纯形法（一）、一般形式：第三十五页，共六十一页。（二）、单纯形法的计算准则1)∵minz，∴所有cj-zj≥0为最优准则。2)检验是否为满意解。∵非基变量的检验数含Pk，即cj-zj=ΣαkjPk，(k=1,2,…,k；j=1,2,…,n)∴首先检查αkj

是否全部为零？如果αkj

全部为零，则表示目标均已全部达到，获得满意解，停止计算转到第(5)步；否则转入(2)。第三十六页，共六十一页。(1)建立初始单纯形表。一般假定初始解在原点，即以约束条件中的所有负偏差变量或松弛变量为初始基变量，按目标优先等级从左至右分别计算出各列的检验数，填入表的下半部。（三）、单纯形法的计算步骤第三十七页，共六十一页。在Pk行，从负检验数中，选绝对值最大者，对应的变量xs就是进基变量。若Pk行中有几个相同的绝对值最大者，则依次比较它们各列下部的检验数，取其绝对值最大的负检验数的所在列的xs为进基变量。假如仍无法确定，则选最左边的变量（变量下标小者）为进基变量。(2)检验是否为满意解。首先检查检验数αkj

(k=1,2,…,k)是否全部为零？如果全部为零，则表示目标均已全部达到，获得满意解，停止计算转到第(5)步；某一个αkj<0，并且Pk这一行的检验数σkj<0

(j=1,2,…,n+2m)，应继续改进，转到第(3)步。

第三十八页，共六十一页。(3)确定出基变量其方法同线性规划，即依据最小比值法则故确定xr为出基变量，ers为主元素。若有几个相同的行可供选择时，选最上面那一行所对应得变量为xr。(4)旋转变换（变量迭代）。以为主元素进行变换，得到新的单纯形表，获得一组新解，返回到第(2)步。(5)对求得的解进行分析若计算结果满意，停止运算；若不满意，需修改模型，即调整目标优先等级和权系数，或者改变目标值，重新进行第(2)步。第三十九页，共六十一页。例4：用单纯形法求解例2的目标规划问题第四十页，共六十一页。例4：用单纯形法求解例2的目标规划问题

解：将例2化为标准型第四十一页，共六十一页。θ=min｛－,10/2,56/10,11/1｝=5，故为换出变量。Cj

0000P1

P2

P2P3

0CBXBbx1x2

x3

0

x3

11211000000001－101－10000P210120001－100

P3

56810000001－1σkjP1

0000010000P2

－10－1－20000200P3

－56－8－100000001表4-1第四十二页，共六十一页。θ=min｛10/3,10,6/3,12/3｝=2,故为换出变量。Cj

0000P1

P2

P2P3

0CBXBbx1x2

x3

0

x3

63/20100-1/21/200053/2001－11/2-1/2000x251/210001/2-1/200

P3

630000-551－1σkjP1

0000010000P2

0000001100P3

－6－300005-501表4-2第四十三页，共六十一页。最优解为x1＝2，x2＝4。图4-1的G(2,4)点，但非基变量的检验数为零，故此题有无穷多最优解。θ=min｛4,24,－,6｝=4,故为换出变量。表4-3Cj

0000P1

P2

P2P3

0CBXBbx1x2

x3

0

x3

3001002-2-1/21/2020001－13-3-1/21/20x24010004/3-4/3-1/61/60x1210000-5/35/31/3-1/3σkjP1

0000010000P2

0000001100P3

0000000010第四十四页，共六十一页。⑴⑵⑶⑷GD结论：有无穷多最优解，G(2,4)～D(10/3,10/3)x2x1第四十五页，共六十一页。Cj

0000P1

P2

P2P3

0CBXBbx1x2

x3

0

x3

1001-1－1-1100040002-26-6-110x210/3010-1/31/31/3-1/3000x110/31002/3-2/31/3-1/300σkjP1

0000010000P2

0000001100P3

0000000010最优解为x1＝10/3,，x2=10/3。图4-1的D(10/3,10/3)点。表4-4第四十六页，共六十一页。例d、用单纯形法求解下列目标规划问题

第四十七页，共六十一页。Cj00P1000000000000002.5P20P200000P30000CBXBbx1x2P1250030121－1000000014021001－100000601000001－1000100010000001－1σkjP1

-2500－30－1201000000P2

000000002.501P3

00000010000θ=min｛2500/30,140/2,60/1｝=60,故为换出变量。第四十八页，共六十一页。Cj

00P100P302.5P20P2CBXBbx1x2P17000121－100－30300002001001－1－22000x1601000001－1000100010000001－1σkjP1

－7000－12010030－3000P2

000000002.501P3

00000010000θ=min｛700/30,20/2,－,－｝=10,故为换出变量。第四十九页，共六十一页。Cj

00P100P302.5P20P2CBXBbx1x2P14000-31-1-151500002.5P21001/2001/2-1/2-11000x17011/2001/2-1/200000100010000001-1σkjP1

-400030115-150000P2

-250-5/400-5/45/45/2001P3

00000010000θ=min｛400/15,－,－,－｝=10,故为换出变量。第五十页，共六十一页。Cj

00P100P302.5P20P2CBXBbx1x2P380/30-1/51/15-1/15-1100002.5P270/302/51/30-1/3000-11000x1250/312/51/30-1/300000000100010000001－1σkjP1

00010000000P2

-175/30-1-1/121/12002/5001P3

-80/301/5-1/151/15100000θ=min｛－,350/6,1250/6,100/1｝=75,故为换出变量。第五十一页，共六十一页。Cj

00P100P302.5P20P2CBXBbx1x2P3115/3001/12-1/12-11-1/21/2000x2175/3011/12-1/1200-5/25/2000x160100000-11000125/300-1/121/12005/2-5/21－1σkjP1

00010000000P2

000000005/201P3

-115/300-1/121/12101/2-1/200表中α3＝115/3≠0，说明P3优先等级目标没有实现，但已无法改进，得到满意解

x1＝60，x2＝175/3，＝115/3，＝125/3。第五十二页，共六十一页。

结果分析：计算结果表明，工厂应生产A产品60件，B产品175/3件，2500元的利润目标刚好达到。＝125/3，表明产品比最高限额少125/3件，满足要求。＝115/3表明甲资源超过库存115/3公斤，该目标没有达到。从表中还可以看到，P3的检验数还有负数，但其高等级的检验数却是正数，要保证P1目标实现，P3等级目标则无法实现。所以，按现有消耗水平和资源库存量，无法实现2500元的利润目标。可考虑如下措施：降低A、B产品对甲资源的消耗量，以满足现有甲资源库存量的目标；或改变P3等级目标的指标值，增加甲资源115/3公斤。若很难实现上述措施，则需改变现有目标的优先等级，以取得可行