人教A版2003课标高中数学必修1第三章3.1.1方程的根与函数的零点.ppt课件

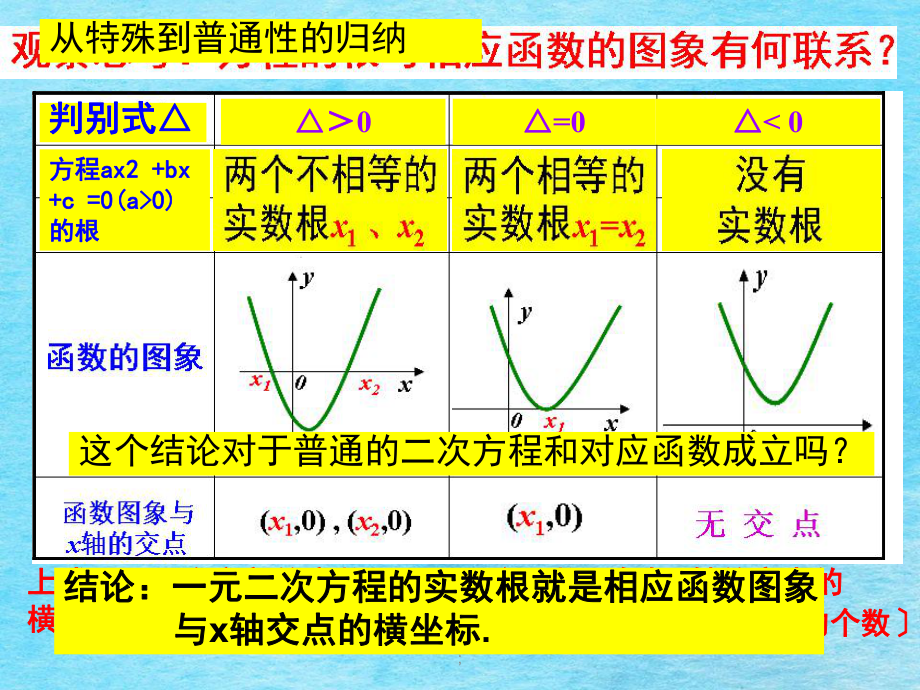
1、;15:43解方程：解方程：；023x引例. 062ln xx；0232 xx1.1.了解函数零点的概念，掌握函数了解函数零点的概念，掌握函数 零点的求法重点；零点的求法重点；2.2.领会函数零点与相应方程的根及领会函数零点与相应方程的根及 函数的图象与函数的图象与x x轴的交点三者之轴的交点三者之 间的的等价关系重点；间的的等价关系重点；3.3.掌握零点存在性定理及其拓展掌握零点存在性定理及其拓展 运用难点运用难点;上述一元二次方程的实数根上述一元二次方程的实数根 二次函数图象与二次函数图象与x x轴的交点的轴的交点的横坐标横坐标( (方程实数根的个数就是对应函数图象与方程实数根的个数就是对

2、应函数图象与x x轴的交点的个数轴的交点的个数判别式判别式方程方程ax2 +bxax2 +bx+c =0(a0)+c =0(a0)的根的根0=0 0这个结论对于普通的二次方程和对应函数成立吗？从特殊到普通性的归纳结论：一元二次方程的实数根就是相应函数图象结论：一元二次方程的实数根就是相应函数图象 与与x轴交点的横坐标轴交点的横坐标.;062ln xx62lnxxy; 对于函数对于函数 y = f(x) , y = f(x) ,使使 f(x) = 0 f(x) = 0 的实数的实数x x叫做函数的零点叫做函数的零点. .;15:43方程方程f(x)=0的实数根的实数根函数函数y=f(x)的图象与

3、的图象与x轴的交点的横坐标轴的交点的横坐标函数函数y=f(x)的零点的零点探求二：函数零点的等价关系探求二：函数零点的等价关系小惊喜：探求函数小惊喜：探求函数y=f(x)y=f(x)的零点的两条途径的零点的两条途径. .15:43知偶函数知偶函数 在在 时的图象时的图象如下图如下图, ,那么此函数零点那么此函数零点的个数是的个数是_._.4; 42)(xxf34)(2xxxf求以下函数的零点求以下函数的零点.思索：能否一切的函数都有零点呢？ 如今有两组镜头如图，哪一组如今有两组镜头如图，哪一组能阐明能阐明A同窗的行程一定曾横穿马路同窗的行程一定曾横穿马路? 探求三：零点存在性定理探求三：零点存

4、在性定理;15:43 第第1 1组情况，假设将马路笼统成组情况，假设将马路笼统成 x x 轴，轴，前后的两个位置视为前后的两个位置视为A A、B B两点请用连两点请用连续不断的曲线画出她的能够途径续不断的曲线画出她的能够途径Oyxy0AB探求三：零点存在性定理探求三：零点存在性定理 假设所画曲线能表示函数的图象，设A点横坐标为a,B点横坐标为b，问：函数在区间(a,b)内一定存在零点吗？探求三：零点存在性定理探求三：零点存在性定理;15:43 假设函数的图象不是延续不断的，函数一定存在零点吗？探求三：零点存在性定理探求三：零点存在性定理探求三：零点存在性定理探求三：零点存在性定理 假设函数假设

5、函数y=f(x)在区间在区间a,b上的图象上的图象是是_的一条曲线，并且有的一条曲线，并且有f(a)f(b)_0，那么，函数那么，函数y=f(x)在区间在区间(a,b) 内有零点内有零点. 即存在即存在 c(a,b) ，使得，使得 f(c) =0， 这个这个c也就是方程也就是方程 f(x)=0 的根的根.延续不断延续不断;探求三：零点存在性定理探求三：零点存在性定理;15:43探求三：零点存在性定理探求三：零点存在性定理假设不成立，利用图象举出反例假设不成立，利用图象举出反例15:43学会了吗? . 假设函数假设函数y=f(x)在区间在区间a,b上的图象上的图象是延续不断的一条曲线，并且有是延

6、续不断的一条曲线，并且有 f(a)f(b)0， 那么，函数那么，函数y=f(x)在区间在区间(a,b) 内有零点内有零点.给定理添加什么条件时给定理添加什么条件时, ,函数在区间函数在区间(a,b)(a,b)上只需一个零点上只需一个零点? ?且是单调函数独一的一个零点.探求四：零点存在性定理的拓展探求四：零点存在性定理的拓展;15:43 -4-1.31.13.45.67.89.912.014.2零点存在性定理的运用 1 2 3 4 5 6 7 8 9解：用计算器或计算机作出解：用计算器或计算机作出x x、f(x)f(x)的对应值表如下的对应值表如下: :例例.判别函数判别函数 f (x) =

7、lnx + 2x 6能否有零点，假设有，能否有零点，假设有， 说出零点的个数，假设没有，阐明理由说出零点的个数，假设没有，阐明理由.这阐明函数这阐明函数f(x)在区间在区间(2,3)内有零点内有零点, 0)3(, 0)2(ff0,(3)(2) ff由于函数由于函数f(x)在定义域在定义域(0,+)内是增函数内是增函数,所以它仅有一个零点所以它仅有一个零点.062ln xx62lnxxy细细 数数 收收 获获函数零点的概念函数零点的概念等价关系等价关系 函数零点的存在性定理函数零点的存在性定理知识点知识点数学思想方法数学思想方法领会函数与方程和数形结合的数学思想领会函数与方程和数形结合的数学思想完成学案完成学案; ; ( (选做选做) )教材教材8888页课后练习第页课后练习第2 2题题. .课课 后后 作作 业业记忆口诀：零点不是点；等价三相连上下不延续；零点可呈现;A .1 B.