第25-26课时三角函数的图象和性质（1）_第1页
第25-26课时三角函数的图象和性质（1）_第2页
第25-26课时三角函数的图象和性质（1）_第3页
第25-26课时三角函数的图象和性质（1）_第4页
第25-26课时三角函数的图象和性质（1）_第5页
全文预览已结束

下载本文档

版权说明：本文档由用户提供并上传，收益归属内容提供方，若内容存在侵权，请进行举报或认领

文档简介

1、盐城市2009届高三艺术生数学一轮复习教学案§25 三角函数的图象（1）【考点及要求】1 了解正弦、余弦、正切函数图象的画法，会用“五点法”画正弦、余弦函数和函数的简图，2 掌握由函数的图象到函数的图象的变换原理【基础知识】1“五点法”画正弦、余弦函数和函数的简图，五个特殊点通常都是取三个 点，一个最 点，一个最 点；2 由函数的图象到函数的图象的变换方法之一为：将的图象向左平移个单位得 图象，再保持图象上各点纵坐标不变，横坐标变为原来的 得图象，再保持图象上各点横坐标不变，纵坐标变为原来的 倍得图象，最后将所得图象向 平移个单位得的图象这种变换的顺序是：相位变换周期变换振幅变换。若

2、将顺序改成呢？【基本训练】1函数的振幅是,频率是,初相是2用“五点法”画函数的图象时，所取五点为 3函数的图象与直线交点个数是个4如果把函数的图象向右平移2个单位后所得图象的函数解析式为 5函数的图象过点则的一个值是 【典型例题讲练】例1试说明下列函数的图象与函数图象间的变换关系： (1) (2) (3)例2（1）将函数的周期扩大到原来的2倍，再将函数图象左移，得到图象对应解析式是 （2）若函数图象上每一个点的纵坐标保持不变，横坐标伸长到原来的两倍，然后再将整个图象沿轴向右平移个单位，向下平移3个单位，恰好得到的图象，则 （3）先将函数的图象向右平移个单位长度，再将所得图象作关于轴的对称变换，

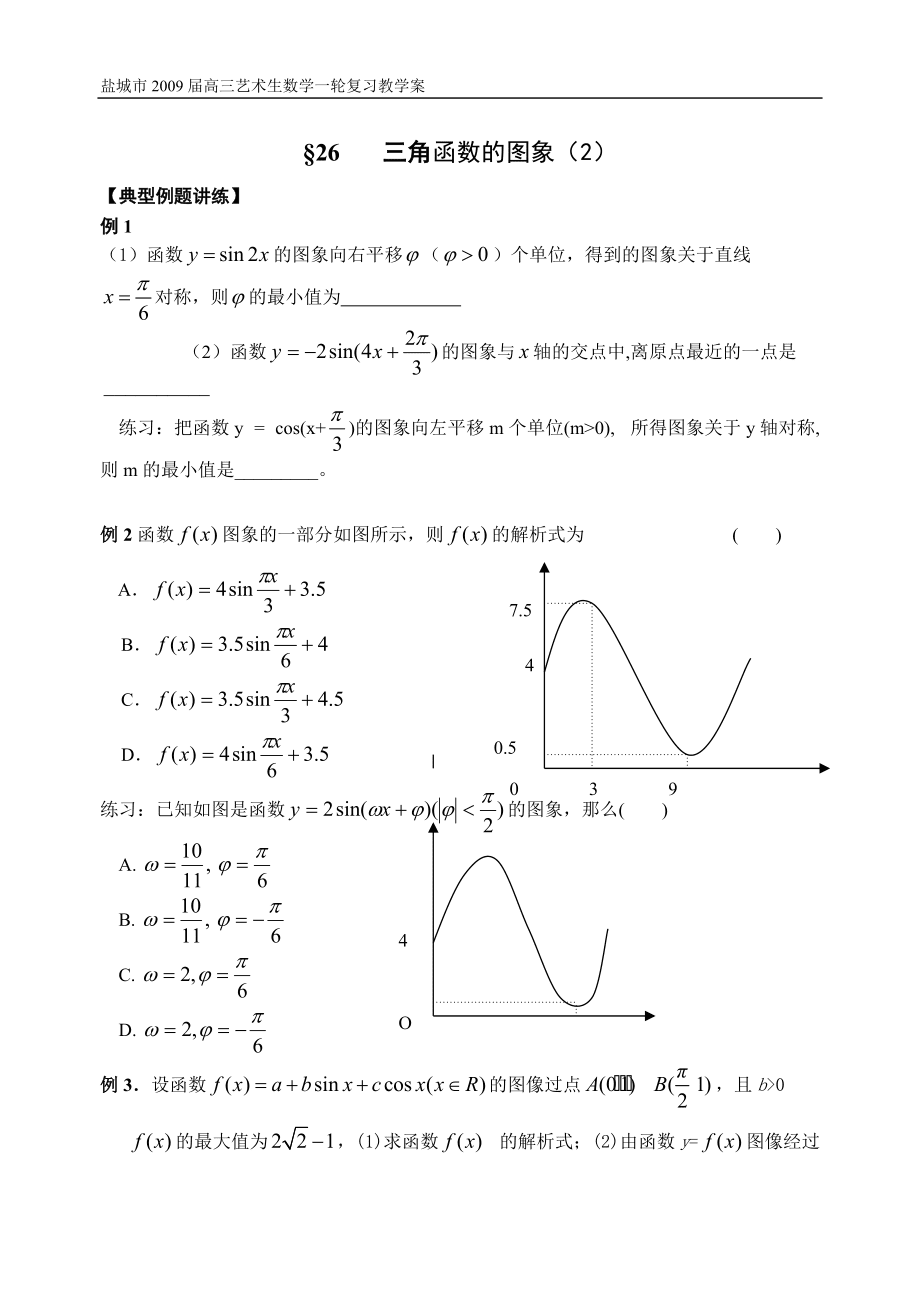
3、则所得函数图象对应解析式为 例3已知函数，用“五点法”画出它的图象；求它的振幅，周期及初相；说明该函数的图象可由的图象经怎样的变换得到？【课堂小结】12【课堂检测】 1要得到函数的图象，只需将函数图象上的点的坐标到原来的倍，再向平移个单位2将函数的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)，再将所得的图象向左平移个单位，所得的图象对应的解析式是 13如图所示为,在上的图象，则它们所对应的图象编号顺序是( )A. B.C. D.§26 三角函数的图象（2）【典型例题讲练】例1 （1）函数的图象向右平移（）个单位，得到的图象关于直线对称，则的最小值为 （2）函数的图象与轴的交点中

4、,离原点最近的一点是练习：把函数y = cos(x+)的图象向左平移m个单位(m>0), 所得图象关于y轴对称, 则m的最小值是_。例2函数图象的一部分如图所示，则的解析式为 ( )47.50.5390 ABCD练习：已知如图是函数的图象，那么( )A. 4B. C. OD. 例3设函数的图像过点，且b>0的最大值为，(1)求函数 的解析式；(2)由函数y=图像经过平移是否能得到一个奇函数y=的图像？若能，请写出平移的过程；若不能，请说明理由。【课堂小结】 【课堂检测】1若函数（）的最小值为，周期为，且它的图象过点，求此函数解析式 202已知函数（）的一段图象如下图所示，求函数的解析式【课后作业】1已知函数（），该函数的图象可由（）的图象经过怎样的变换得到？2已知函数 求

人人文库> 全部分类> 教育资料 > 课件下载

温馨提示

  • 1. 本站所有资源如无特殊说明，都需要本地电脑安装OFFICE2007和PDF阅读器。图纸软件为CAD,CAXA,PROE,UG,SolidWorks等.压缩文件请下载最新的WinRAR软件解压。
  • 2. 本站的文档不包含任何第三方提供的附件图纸等，如果需要附件，请联系上传者。文件的所有权益归上传用户所有。
  • 3. 本站RAR压缩包中若带图纸，网页内容里面会有图纸预览，若没有图纸预览就没有图纸。
  • 4. 未经权益所有人同意不得将文件中的内容挪作商业或盈利用途。
  • 5. 人人文库网仅提供信息存储空间，仅对用户上传内容的表现方式做保护处理，对用户上传分享的文档内容本身不做任何修改或编辑，并不能对任何下载内容负责。
  • 6. 下载文件中如有侵权或不适当内容，请与我们联系，我们立即纠正。
  • 7. 本站不保证下载资源的准确性、安全性和完整性, 同时也不承担用户因使用这些下载资源对自己和他人造成任何形式的伤害或损失。

最新文档

评论

0/150

提交评论