枣一高二文导数几何意义1

1、3.1.3导数的几何意义枣庄一中 苏增传一、教学目标重点：理解和掌握切线的新定义、导数的几何意义，体会数形结合、以直代曲的思想方法.难点：发现、理解及应用导数的几何意义知识点：导数的几何意义以及对曲线切线方程的求解.能力点：通过探究导数的几何意义和曲线的切线方程的求法，体会“以直代曲”的数学思想方法和培养学生运用数形结合思想解决问题的能力教育点：通过设计环环相扣的问题，引导学生主动地参与探究活动，体验学习的乐趣，养学生良好的思维品质，激发他们的学习热情.自主探究点：导数的几何意义和“以直代曲”的数学思想方法.考试点：求曲线的切线方程. 易错易混点： “以直代曲”的思想容易误解的是用直线去代替某

2、一段曲线.拓展点：当切点不在曲线上求曲线的切线方程.二、复习引人前面我们学习了函数在处的导数就是函数在该点处的瞬时变化率.问题1： 求导数的步骤有哪几步？学生回答：第一步：求平均变化率；第二步：求瞬时变化率.（即，平均变化率趋近于的确定常数就是该点的导数）问题2：观察函数的图象，平均变化率 在图形中表示什么？x1x2Oxx2-x1=xf(x2)-f(x1)=yPyf(x1)y=f(x)f(x2)学生回答：平均变化率表示割线的斜率.这就是平均变化率（）的几何意义，那么瞬时变化率()在图中又表示什么呢？今天我们就来探究导数的几何意义.【设计意图】突破平均变化率的几何意义，后面在表示割线斜率时能直接

3、联系此知识.同时引出本节课的研究问题导数几何意义是什么？三、探究新知 1.切线的新定义：要研究导数的几何意义，结合导数的概念，即要探究，割线的变化趋势.问题1：初中平面几何中圆的切线的定义是什么？学生回答：直线和圆有唯一公共点时，直线叫做圆的切线，唯一公共点叫做切点问题2：曲线在点处的切线能用直线与切线的公共点个数来定义吗？你能否用你已经学过的函数曲线的切线举出反例？回答：正弦函数的曲线与直线可能相切时有两个公共点圆是一种特殊的曲线，这种定义并不适用于一般曲线的切线如图曲线，直线虽然与曲线有惟一公共点，但它与曲线不相切；而另一条直线，虽然与曲线有两个公共点和，但与曲线相切于点因此，直线与曲线的

4、公共点的个数不能用来定义一般曲线的切线，我们必须用新的方法来定义曲线的切线【设计意图】概念的辨析有助于学生准确理解概念，避免了学习的负向迁移.通过普通曲线的切线与圆的切线对比，使学生认识到曲线的切线不能以直线与曲线的交点个数决定.由此提出：如何定义曲线上某点的切线呢？激发学生的求知欲望，进入本节课重点内容的探索过程.用多媒体演示动画（几何画板）（1）圆中割线逼近切线：ABTxyO圆上点A处的切线AT和割线AB，演示点B从右边沿着圆逼近点A ,然后再从左边沿着圆逼近点A ，即，割线AB的变化趋势.思考：观察割线与切线是否有某种内在联系呢？结论：（先感知后发现）当，随着点B沿着圆逼近点A，割线AB

5、无限趋近于点A处的切线AT.【设计意图】带着问题观察动画，借助熟悉的圆中的某点处的割线和切线，学生更易感知当，割线的变化趋势，同时用逼近的方法体会割线逼近切线，消除学生对极限的神秘感.（2）把割线逼近切线的结论从圆推广到一般曲线：OxyP割线切线Ty=f(x)多媒体动态演示教材77页，当点沿着曲线趋近点时，割线的变化趋势图. 引导学生类比（1），分析当点沿着曲线趋近于点时，即，研究割线的变化趋势.【设计说明】教师用多媒体动画演示，学生观察并讨论.【设计意图】通过多媒体动画的演示，探索一般曲线中的切线定义，让学生借助直观的图象感知和发现，得出：，割线趋于确定位置的直线定义为切线.结论：点趋近于点

6、时，割线趋近于确定的位置，为曲线的切线. 一般曲线的切线定义：当点沿着曲线逼近点时，即，割线趋近于确定的位置，这个确定位置上的直线PT称为点P处的切线.了解“以直代曲”的思想引导学生观察：在点的附近，比更接近曲线，比更接近曲线，过点的切线最贴近附近的曲线因此，在点的附近，曲线可以用过点的切线近似代替“以直代曲”的数学思想方法，是微积分学中的重要思想方法【设计意图】通过动画演示，让学生形象而逼真的直观感知 “以直代曲”思想.2. 导数的几何意义：1.已知曲线上两点：思考1：根据切线定义可知：，割线趋近于切线PT .那么割线的斜率与切线PT的斜率又有何关系？学生回答： 思考2：对比“时，平均变化率

7、趋近的确定常数就是瞬时变化率”，又割线的斜率对应平均变化率，那么切线的斜率对应什么？学生回答：切线的斜率对应该点处的瞬时变化率，即该点处的导数. 【设计意图】通过两个思考：（1）先解决割线斜率与切线斜率的关系，（2）再对照平均变化率与瞬时变化率的关系，自然得出切线的斜率对应该点处的瞬时变化率即导数，增加了铺垫问题为学生引导思路，便于学生较好地完成探索活动，主动获得知识.2.结合上面的研究过程，你能指出导数的几何意义吗？函数在处的导数就是曲线在该点处的切线斜率，即：【设计意图】让学生自主探究得出结论，有水到渠成的感觉，避免硬性抛出抽象概念,同时培养学生的归纳概括能力.四、理解新知1.一般曲线切线

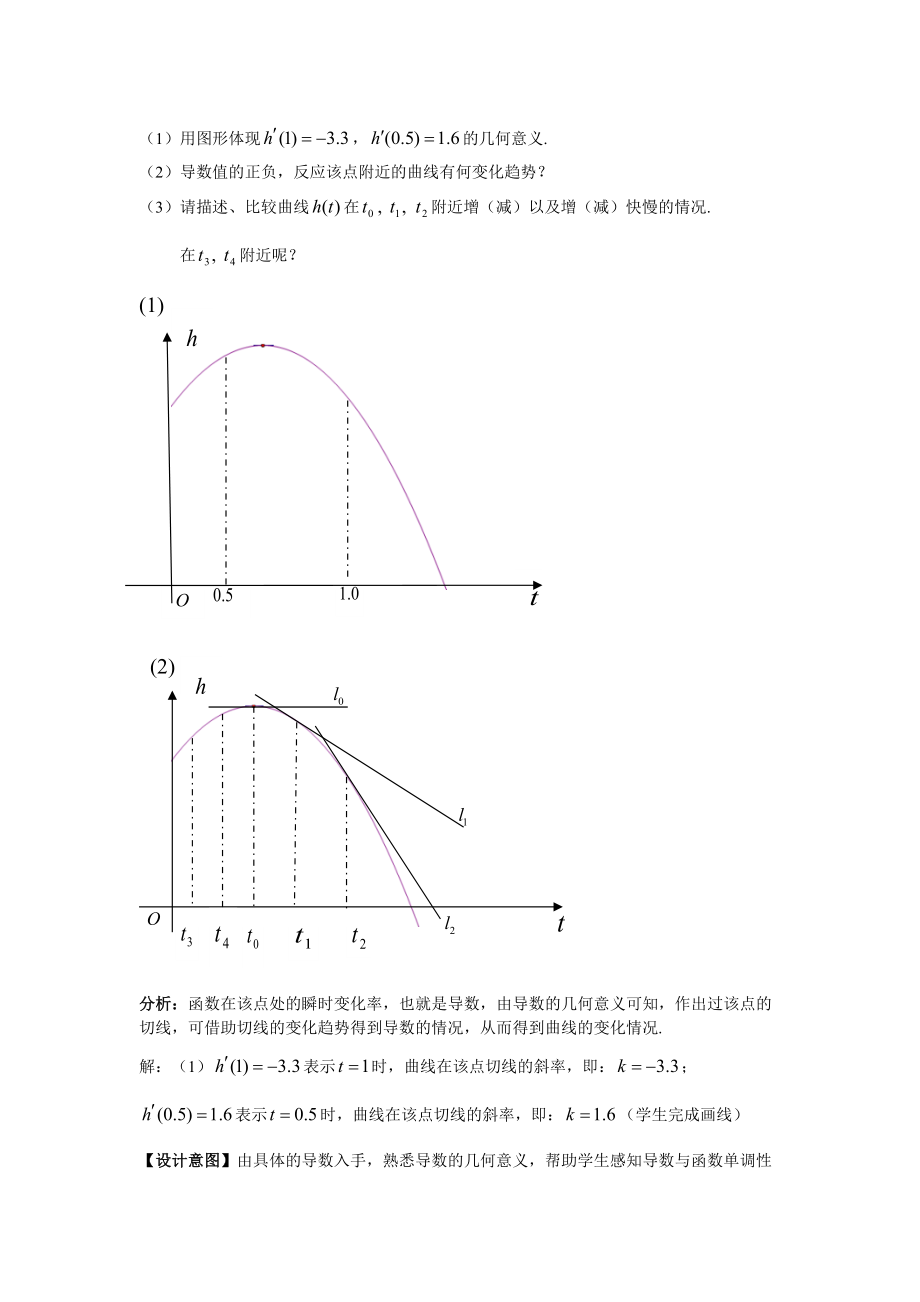
8、的定义：（1）当点沿着曲线逼近点时，即，割线趋近于确定的位置，这个确定位置上的直线PT称为点P处的切线.（2）了解“以直代曲”的思想：某点附近一个很小的研究区域内，曲线与切线的变化趋势基本一致，故可由曲线上某点处的切线近似代替这一点附近的曲线.2.导数的几何意义：（1）割线的斜率是： （2）导数的几何意义:函数在处的导数就是曲线在该点处的切线斜率，即：【设计意图】梳理本节课重点知识，强化记忆，为准确地运用新知，作必要的铺垫.五、运用新知例1如图，它表示跳水运动中高度随时间变化的函数的图象.（1）用图形体现，的几何意义.（2）导数值的正负，反应该点附近的曲线有何变化趋势？（3）请描述、比较曲线在

9、附近增（减）以及增（减）快慢的情况.在附近呢？(1) (2)分析：函数在该点处的瞬时变化率，也就是导数，由导数的几何意义可知，作出过该点的切线，可借助切线的变化趋势得到导数的情况，从而得到曲线的变化情况.解：（1）表示时，曲线在该点切线的斜率，即：；表示时，曲线在该点切线的斜率，即：（学生完成画线）【设计意图】由具体的导数入手，熟悉导数的几何意义，帮助学生感知导数与函数单调性之间的联系.（2）导数值为正，则曲线在该点处得切线的斜率为正，曲线在该点附近单调递增，导数值为负，则曲线在该点处得切线的斜率为负，曲线在该点附近单调递减. 【设计意图】引导学生感知导数反映变化率的本质.(3) 作出曲线在这

10、些点处的切线，在处切线平行于轴，即，说明在时刻附近变化率为0，函数几乎没有增减；在作出切线，切线呈下降趋势，即，函数在点附近单调递减；直线的倾斜程度小于直线的倾斜程度，这说明曲线曲线在附近比在附近下降得缓慢【设计意图】将本例设计多问，降低了台阶分解了难度，使学生更好的理解掌握.问题：如何用导数研究函数的增减？结论：根据导数的几何意义，当某点处导数大于零时，说明在这点的附近曲线是上升的，即函数在这点附近是单调递增；当某点处导数小于零时，说明在这点的附近曲线是下降的，即函数在这点附近是单调递减；当某点处导数等于零时，说明在该点的附近变化率为0，函数几乎没有增减.【设计意图】引领学生对问题进行定性分

11、析，在某点处由切线的“走向”分析曲线的“走向”，渗透“以直代曲”的数学思想变式练习：函数上有一点，求该点处的导数，并由此解释函数的增减情况.函数在定义域上任意点处的瞬时变化率都是3，函数在定义域内单调递增.(此时任意点处的切线就是直线本身，斜率就是变化率)【设计意图】复习导数的求法，加深学生对导数研究函数增减情况应用的认识，也是例题结论的进一步验证.例2.求在点处的切线方程.解： 即切线的斜率，所以，在点处的切线方程为即.【师生活动】总结在曲线上某点切线方程的求解步骤（学生归纳总结，教师演示）（1）求出曲线在点P处的导数即切线的斜率；（2）利用点斜式求切线方程.练习：已知曲线上一点横坐标为-1

12、，求曲线在这点的切线方程.学生板演，师生共同点评.【设计意图】通过学生独立应用导数意义求在某点的曲线的切线方程，培养学生主动探索，解决问题的能力，并且加深学生对导数几何意义的理解，熟练掌握几何意义的应用.六、课堂小结这节课我们学习了哪些知识和方法？学生进行开放式小结：（回顾学习的两个知识和数学思想方法）1.切线的定义：当点沿着曲线逼近点时，即，割线趋近于确定的位置，这个确定位置上的直线称为点处的切线.2.函数在处的导数的几何意义就是函数的图象在处的切线的斜率. 即：导数反映了函数的变化率，从图形上来看，表现为切线的斜率，如果导数为正，则切线的斜率为正，切线呈上升趋势，曲线在该点附近也是上升趋势，函数单调增；如果导数为负，则切线的斜率为负，切线呈现为下降趋势，曲线在该点附近也是下降趋势，函数单调减.数学思想方法：体会“数形结合”的思想方法、逼近的思想方法、“以直代曲”的思想方法.【设计意图】通过师生共同反思，优化学生的认知结构.七、布置作业必做题：课本79页A组1,2,5选做题：B组1,2,3八、教后反思：本节课的亮点：1.多媒体课件动画演示较好，使抽象的概念变得在图形的直观演示下，容易理解；2.知识得来让学生探究得出，在教学的过程中加强了对学生观察能力，独立思考能力，理解归纳能力，及数形结合能力的训练；3.及时对学生所取得的成绩进行肯定，从而使学生获得成就感，增强