济南大学数据结构(Java版)

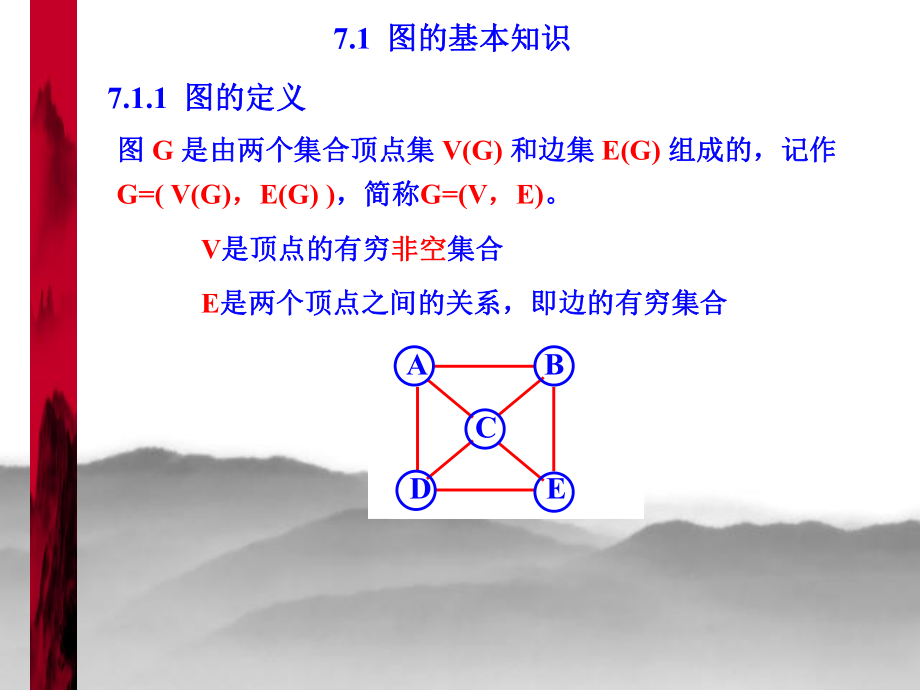
1、数据结构（数据结构（Java版）版）|第第1章章 绪论绪论|第第2章章 线性表线性表|第第3章章 串串|第第4章章 栈与队列栈与队列|第第5章章 数组和广义表数组和广义表|第第6章章 树和二叉树树和二叉树第第7章章 图图|第第8章章 查找查找|第第9章章 排序排序第七章第七章 图图图是一种较线性表和树更为复杂的数据结构图是一种较线性表和树更为复杂的数据结构。线性表线性表: 线性结构（前驱、后继）线性结构（前驱、后继）树树: 层次结构（父子）层次结构（父子）图图: 任意两个数据元素之间都可能相关（邻接）任意两个数据元素之间都可能相关（邻接） ABCDE7.1 图的基本知识图的基本知识图图 G 是

2、由两个集合顶点集是由两个集合顶点集 V(G) 和边集和边集 E(G) 组成的，记作组成的，记作G=( V(G)，E(G) )，简称，简称G=(V，E)。ABCDEABCDEV是顶点的有穷是顶点的有穷非空非空集合集合 ABCDEE是两个顶点之间的关系，即边的有穷集合是两个顶点之间的关系，即边的有穷集合 7.1.1 图的定义图的定义无向图和有向图无向图和有向图 1. 无向图无向图: 边是顶点的无序对，即边没有方向性。边是顶点的无序对，即边没有方向性。v1v2v3v5v4V = v1 , v2 , v3 , v4 , v5 E = ( v1 , v2 ) , ( v1 , v4 ) , ( v2 ,

3、 v3 ) , ( v2 , v5 ) , ( v3 , v4 ) , ( v3 , v5 ) ( v1 , v2 )表示顶点表示顶点 v1 和和 v2 之间的边之间的边( v1 , v2 ) = ( v2 , v1 )2. 有向图有向图: 其边是顶点的有序对，即边有方向性。其边是顶点的有序对，即边有方向性。v1v2v4v3V = v1 , v2 , v3 , v4 E = , , , 通常有向图的边称为通常有向图的边称为弧弧，表示顶点表示顶点 v1 到到 v2 的弧。的弧。称称 v1 为为弧尾弧尾，称，称 v2 为为弧头弧头。 有有 n(n- -1) 条边的无向图称为条边的无向图称为完全图完

4、全图。 12v1v2v4v3有有 n(n-1) 条弧的有向图称为条弧的有向图称为有向完全图有向完全图。 v1v2v33. 完全图、有向完全图完全图、有向完全图4. 带权无向图带权无向图(无向网无向网) 和和 带权有向图带权有向图(有向网有向网)有时对图的边或弧赋予相关的数值，这种与图的边或弧相有时对图的边或弧赋予相关的数值，这种与图的边或弧相关的数值叫做关的数值叫做权权。 带权的有向图称为带权的有向图称为有向网有向网。带权的无向图称为带权的无向图称为无向网无向网。ABCDE53821497距距离离耗耗费费这种带权的图通常称为这种带权的图通常称为网网。 5. 邻接与关联邻接与关联对于无向图对于无

5、向图 G=(V, E)，如果，如果边边 (v, v) E，则称顶点，则称顶点 v 和和 v 互为互为邻接点，即邻接点，即 v 和和 v 相相邻接邻接。 边边 (v, v) 依附于顶点依附于顶点 v 和和 v ，或者说，或者说 (v, v) 与顶点与顶点 v 和和 v 相相关联关联。 对于有向图对于有向图 G=(V, E) ，如果，如果弧弧 E，则称顶点，则称顶点 v 邻接到邻接到顶顶点点 v，顶点，顶点 v 邻接自邻接自顶点顶点 v 。 vvvv弧弧 和顶点和顶点 v, v 相相关联关联。7.1.2 结点的度结点的度对于无向图，对于无向图，结点结点 v 的度的度是和是和 v 相关联的边的数目，

6、记做相关联的边的数目，记做TD(v)。 v1v2v3v5v4顶点顶点 v3 的度为的度为 31. 度、入度、出度度、入度、出度对于有向图，对于有向图，顶点顶点 v 的的度度 TD(V) 分为两部分分为两部分出度出度、入度入度。 以结点以结点 v 为为终点终点的弧的数目称为的弧的数目称为 v 的的入度入度，记为，记为ID(v) ；以结点以结点 v 为为起点起点的弧的数目称为的弧的数目称为 v 的的出度出度，记为，记为OD(v)； 顶点顶点 v 的度的度为为 TD(v) = ID(v) + OD(v)。 v1v2v4v3顶点顶点 v1 的出度为的出度为 2顶点顶点 v1 的入度为的入度为 1顶点顶

7、点 v1 的度为的度为 3性质性质: 对于一个图对于一个图(无向图、有向图无向图、有向图)，如果结点，如果结点 vi 的度为的度为TD(vi)，那么具有那么具有 n 个顶点、个顶点、e 条边或弧的图，必满足如下关系条边或弧的图，必满足如下关系e = TD(vi)12i = 1n无向图、有向图的边或弧均计算两遍。无向图、有向图的边或弧均计算两遍。v1v2v3v5v4v1v2v4v32. 度与边的关系度与边的关系当当G为有向图时，上式可写为：为有向图时，上式可写为： ID(vi)=i = 1ni = 1n OD(vi)=e TD(vi)=i = 1ni = 1nOD(vi)=2ei = 1n ID

8、(vi)+7.1.3 子图子图假设有两个图假设有两个图 G=(V, E) 和和 G=(V, E) ，如果，如果 V V，且且 E E，并且，并且EE中的边所关联的结点都在中的边所关联的结点都在VV中，则中，则称称 G 为为 G 的的子图子图。 v1v2v4v3求子图求子图v1v1v3v1v4v3v1v2v4v3v1v2v4v3v1v2v3v5v4子图有子图有v1v2v3v5v1v2v5v4v1v2v3v5v47.1.4 路径、回路及连通性路径、回路及连通性无向图无向图 G 中若存在一条有穷非空序列中若存在一条有穷非空序列 w = v0 e1 v1 e2 v2 ek vk ，其，其中中 vi 和

9、和 ei 分别为顶点和边，则称分别为顶点和边，则称 w 是从顶点是从顶点 v0 到到 vk 的一条的一条路径路径。顶点顶点 v0 和和 vk 分别称为路径分别称为路径 w 的的起点起点和和终点终点。路径的长度路径的长度是路径上的是路径上的边的数目边的数目。w 的长度为的长度为 kv0v1v2vk- -1vk. . .e1e2ek起点和终点相同且长度大于起点和终点相同且长度大于1的简单路径称为的简单路径称为回路回路。如果在一条路径中，除起点和终点外，其他结点都不相同，则此路如果在一条路径中，除起点和终点外，其他结点都不相同，则此路径称为径称为简单路径简单路径。1. 路径、路径长度、回路路径、路径

10、长度、回路 带权图中，从起点到终点的路径上各条边的权值之和称为这条带权图中，从起点到终点的路径上各条边的权值之和称为这条路径的路径长度。路径的路径长度。v1v4v529v2v365387 从结点从结点v1到到v5的一条路径（的一条路径（v1，v4，v5）的路径长度是）的路径长度是2+9=11。 一个有向图一个有向图G中，若存在一个结点中，若存在一个结点v0，从，从v0有路径可以到达图有路径可以到达图G中其他所有结点，则称此有向图为中其他所有结点，则称此有向图为有根的图有根的图，称，称v0为图为图G的的根根。2. 有根的图和图的根有根的图和图的根3. 连通图连通图无向图无向图G，如果从顶点，如果

11、从顶点 v 到顶点到顶点 v 有路径，则称有路径，则称 v 和和 v 是是连通连通的。的。 如果对于如果对于无向图无向图 G 中中任意任意两个顶点两个顶点 vi , vj V, vi 和和 vj 都是都是连通连通的，的，则称则称 G 是是连通图连通图。 v1v2v3v5v4是否为连通图是否为连通图连通分量连通分量指的是无向图中的指的是无向图中的极大连通子图极大连通子图。 ABCLHDEFGH非连通图非连通图连通分量为连通分量为ABCLHDEFGH：将图中：将图中, ,任何不在连通子图中的顶点任何不在连通子图中的顶点, ,加到子图中后，子图就加到子图中后，子图就。连通图的连通图的连通分量是其自身

12、连通分量是其自身而非连通图而非连通图可以有多个可以有多个有向图有向图G，如果从顶点，如果从顶点 v 到顶点到顶点 v 有路径有路径 或或 从顶点从顶点 v 到顶点到顶点 v 有有路径，则称路径，则称 v 和和 v 是是连通连通的。的。 在在有向图有向图 G 中，如果对于每一对中，如果对于每一对 vi, vj V，vivj ，从，从 vi 到到 vj 和和 从从 vj 到到 vi 都都存在路径，则称存在路径，则称 G 是是强连通图强连通图。 v1v2v4v3是否为强连通图是否为强连通图4. 强连通图强连通图有向图中的有向图中的强连通的最大子图强连通的最大子图称作有向图的称作有向图的强连通分量强连

13、通分量。 v1v2v4v3非强连通图非强连通图强连通分量强连通分量v2v1v4v3注意注意强连通图的强连通图的强连通分量是其自身强连通分量是其自身而非强连通图而非强连通图可以有多个可以有多个7.1.5 生成树生成树一个连通图的一个连通图的是一个极小连通子图。是一个极小连通子图。:在极小连通子图上在极小连通子图上,任一条边子图就任一条边子图就,若再若再一条边一条边,必定构成一个必定构成一个。:所有所有n个顶点个顶点;有有n-1条边条边;图是连通的。图是连通的。V1V2V3V4V5V1V2V3V4V5V1V2V3V4V5图的图的生成树生成树对非连通图，则称由各个连通分量的生成树的集合为对非连通图，

14、则称由各个连通分量的生成树的集合为此非连通图的此非连通图的。性质性质: 一个有一个有n个顶点的连通图的个顶点的连通图的生成树生成树有且仅有有且仅有n- -1条边。条边。1. 如果一棵生成树有如果一棵生成树有 n 个顶点和小于个顶点和小于 n- -1 条边，则为条边，则为非连通图非连通图。2. 如果一棵生成树有如果一棵生成树有 n 个顶点和多于个顶点和多于 n- -1 条边，则一定有条边，则一定有环环。构成一棵构成一棵 n 顶点生成树需要顶点生成树需要 n- -1 条边，条边，少于少于 n- -1 ，则必有边断开，不再连通。，则必有边断开，不再连通。构成一棵构成一棵 n 顶点生成树需要顶点生成树

15、需要 n- -1 条边，条边，若再添加一条边，必会使得与它关联的那两个顶点之间有了若再添加一条边，必会使得与它关联的那两个顶点之间有了第二条路径。第二条路径。ABCLHJ性质性质: 一个连通图的生成树并不唯一一个连通图的生成树并不唯一ABCLHJABCLHJABCLHJ生成树生成树ABCLHJ删除删除环环中的任一条边中的任一条边7.2 图的存储结构图的存储结构顺序存储顺序存储邻接矩阵邻接矩阵链式存储链式存储邻接表邻接表如何表达顶点之间如何表达顶点之间存在的关系存在的关系?7.2.1 邻接矩阵邻接矩阵设图设图 G = ( V ，E ) 具有具有 n(n1) 个个顶点顶点 v1 , v2 , ,

16、vn 和和 m 条条边边或或弧弧 e1 , e2 , , em ，则，则 G 的邻接矩阵是的邻接矩阵是 nn 阶矩阵，记为阶矩阵，记为 A(G) 。其每一个元素其每一个元素 aij 定义为定义为:邻接矩阵存放邻接矩阵存放 n 个个顶点顶点信息和信息和 n2 条条边边或或弧弧信息。信息。aij = 01顶点顶点 vi 与与 vj 不相邻接不相邻接顶点顶点 vi 与与 vj 相邻接相邻接v1v2v4v3例，有向图例，有向图 GA(G) = 1 2 3 412340 1 1 00 0 0 00 0 0 11 0 0 0v1v2v3v5v4例无向图例无向图 G0 1 0 1 01 0 1 0 10 1

17、 0 1 11 0 1 0 00 1 1 0 0A(G) = 1 2 3 4 512345优点优点:1. 容易判断任意两个顶点之间是否有容易判断任意两个顶点之间是否有边边或或弧弧。2. 容易求取各个顶点的容易求取各个顶点的度度。邻接矩阵存储的图类邻接矩阵存储的图类public class Graph1 /以邻接矩阵存储的图类以邻接矩阵存储的图类 protected int n； /图的结点个数图的结点个数 protected int mat； /二维数组存储图的邻接矩阵二维数组存储图的邻接矩阵邻接矩阵的特点邻接矩阵的特点1)判断判断ViVj间是否有边间是否有边(弧弧),只需检查只需检查Aij的

18、值是否非的值是否非0。2)很容易计算顶点的度。很容易计算顶点的度。：顶点：顶点Vi 的度为第的度为第i行行(或第或第j列列)的非零元素个数。的非零元素个数。: 第第的元素之和是顶点的元素之和是顶点 的的; 第第的元素之和是顶点的元素之和是顶点的的。V0V1V2V3V40 1 0 1 01 0 1 0 10 1 0 1 11 0 1 0 00 1 1 0 0V0V1V2V30 1 1 00 0 0 00 0 0 11 0 0 0例例:0行的行的 元素元素:0, =1表示表示:弧存在弧存在例例:2列的列的 元素元素: , 2=1表示表示:弧存在弧存在无向图，顶点无向图，顶点 vi 的的度度是邻接矩

19、阵中第是邻接矩阵中第 i 行行或或第第 i 列的元素之和。列的元素之和。例例 G1中，中，v1 的度为的度为 2 ，v2 的度为的度为 3 。v1v2v3v5v4例无向图例无向图 G0 1 0 1 01 0 1 0 10 1 0 1 11 0 1 0 00 1 1 0 0A(G) = 1 2 3 4 512345v1v2v4v3例有向图例有向图 GA(G) = 1 2 3 412340 1 1 00 0 0 00 0 0 11 0 0 0有向图，顶点有向图，顶点 vi 的的出度出度是邻接矩阵中第是邻接矩阵中第 i 行行的元素之和。的元素之和。顶点顶点 vi 的的入度入度是邻接矩阵中第是邻接矩阵

20、中第 i 列列的元素之和。的元素之和。例例 v1 的度为的度为 2+1=3。无向图的邻接矩阵都是无向图的邻接矩阵都是对称矩阵对称矩阵。有向图的邻接矩阵一般有向图的邻接矩阵一般不对称不对称。1 2 3 412340 1 1 00 0 0 00 0 0 11 0 0 00 1 0 1 01 0 1 0 10 1 0 1 11 0 1 0 00 1 1 0 01 2 3 4 512345无向图无向图有向图有向图v1v2v3v5v4v1v2v4v3无向图可以采用无向图可以采用压缩存储方式压缩存储方式带权图带权图(网网) 的邻接矩阵的邻接矩阵v1v2v3v5v4v65487935651 0 5 7 0

21、4 8 0 9 5 0 6 5 0 A = 1 2 3 4 5 6123456 3 1 0aij = wij若若vi vj，顶点，顶点 vi 与与 vj 相邻接相邻接若若vi vj，顶点，顶点 vi 与与 vj 不相邻接不相邻接0若若vi= vj7.2.2 邻接表邻接表对图中每一个顶点建立一个单链表，指示与该顶点对图中每一个顶点建立一个单链表，指示与该顶点邻接的邻接的顶点顶点和和关关联的联的边边或或弧弧。data next边结点边结点datanext顶点结点顶点结点data : 结点数据元素信息结点数据元素信息next : 与该结点关联的另一条边与该结点关联的另一条边data : 顶点的信息顶

22、点的信息next : 第一条关联边结点第一条关联边结点v1v2v3v5v4e1e2e3e4e5e601234v1v2v3v4v5v4v2v5v3v1v5v4v2v3v1v3v2声明邻接表存储的图类声明邻接表存储的图类import ds_java.OnelinkNode; /单向链表的结点类单向链表的结点类public class Graph2 /以邻接表存储的图类以邻接表存储的图类 private OnelinkNode table； /图的邻接表图的邻接表v1v2v3v5v4无向图无向图 Ge1e2e3e4e5e601234v1v2v3v4v5如何获取顶点的度？如何获取顶点的度？顶点顶点 v

23、i 的度为第的度为第 i 条链中的结点数。条链中的结点数。需要多少存储空间？（需要多少存储空间？（n个结点个结点m条边的无向图）条边的无向图）n + 2mv4v2v5v3v1v5v4v2v3v1v3v2无向图的邻接表的特点无向图的邻接表的特点: 顶点顶点v的的:等于等于v对应对应; 判定两顶点判定两顶点v,w 是否是否:看看v对应邻接链表中对应邻接链表中; 所有邻接链表所有邻接链表;1.在在G中中:要要插入、删除结点；插入、删除结点；V0V1V2V3V40123431 420 431 20 21 V0V1V2V3V4图图G1v1v2v4v3有向图有向图 Ge1e2e3e4如何获取顶点的如何获取

24、顶点的度度？顶点顶点 vi 的的出度出度为为邻接表邻接表第第 i 条链中的结点数。条链中的结点数。为了方便求顶点的为了方便求顶点的入度入度，引入引入逆邻接表逆邻接表需要多少存储空间？（只保需要多少存储空间？（只保留入边表和出边表之一）留入边表和出边表之一）n + m0123v1v2v3v4顶点顶点 vi 的的入度入度为为逆邻接表逆邻接表第第 i 条链中的结点数。条链中的结点数。0123v1v2v3v4v3v2v4v1v4v1v1v3邻接矩阵与邻接表邻接矩阵与邻接表存储空间存储空间求顶点的度求顶点的度求顶点的邻接顶点求顶点的邻接顶点判断两个顶点是否关联判断两个顶点是否关联0 1 0 1 01 0

25、 1 0 10 1 0 1 11 0 1 0 00 1 1 0 01 2 3 4 51234501234v1v2v3v4v5v4v2v5v3v1v5v4v2v3v1v3v27.3 图的遍历图的遍历与树的遍历类似，如果从图中某一顶点出发，以某种次序顺序地与树的遍历类似，如果从图中某一顶点出发，以某种次序顺序地访问图中访问图中所有顶点所有顶点，且使每一个顶点，且使每一个顶点仅仅被访问一次，这一过程称被访问一次，这一过程称为为图的遍历图的遍历。图的遍历算法是求解图的遍历算法是求解图的连通性问题图的连通性问题、生成树生成树、和、和拓扑排序拓扑排序等等算法的基础。算法的基础。通常有两条遍历图的路径通常有

26、两条遍历图的路径: 深度优先搜索遍历深度优先搜索遍历、广度优先搜广度优先搜索遍历索遍历。7.3.1 深度优先遍历深度优先遍历深度优先搜索（深度优先搜索（DFS）遍历是类似于树的）遍历是类似于树的先序遍历先序遍历的一种方法。的一种方法。v1v2v3v5v4v6v7v8图可分为三部分图可分为三部分:基结点基结点第一个第一个邻接结点邻接结点所能导出的所能导出的子图子图其它其它邻接顶点所邻接顶点所能导出的能导出的子图子图1 深度优先遍历算法描述深度优先遍历算法描述从图中选定的一个结点从图中选定的一个结点v0出发，访问出发，访问v0。 查找与查找与v0有边相连且未被访问过的另一个结点有边相连且未被访问过

27、的另一个结点vj。 若有若有vj，从，从vj出发继续进行深度优先搜索遍历。出发继续进行深度优先搜索遍历。 若找不到若找不到vj，说明从，说明从v0开始能够到达的所有结点都已被访问开始能够到达的所有结点都已被访问过，遍历结束。过，遍历结束。v1v2v3v5v4v6v7v8过程分析过程分析v1v2v3v4v6v8v5v7深度优先搜索顺序深度优先搜索顺序: v1v2v4v8v5v3v6v72 以邻接矩阵存储的图的深度优先遍历算法实现以邻接矩阵存储的图的深度优先遍历算法实现 在以邻接矩阵存储的图在以邻接矩阵存储的图Graph1类中，增加一个一维数组成员类中，增加一个一维数组成员变量变量visited和

28、一个成员方法和一个成员方法depthfs()。 visited用于标志图中结点是否已被访问。每个数组元素对应用于标志图中结点是否已被访问。每个数组元素对应图的一个结点，若一个结点已被访问，则相应的数组元素被置图的一个结点，若一个结点已被访问，则相应的数组元素被置为为1，否则为，否则为0。构造方法中创建。构造方法中创建visited数组，其元素值全为数组，其元素值全为0，表示初始状态是图中所有结点均未被访问过。表示初始状态是图中所有结点均未被访问过。 depthfs()方法实现图的深度优先遍历算法。方法实现图的深度优先遍历算法。2以邻接矩阵存储的图的深度优先遍历算法实现以邻接矩阵存储的图的深度优

29、先遍历算法实现package ds_java;public class Graph1 /以邻接矩阵存储的图类 protected int n; /图的结点个数 protected int mat; /二维数组存储图的邻接矩阵 protected int visited; /访问标记数组 public Graph1(int m1) n=m1.length; mat=new intnn; System.arraycopy(m1,0,mat,0,n); /System类方法，复制数组 visited=new int n; public Graph1()【例【例7.1】 以邻接矩阵表示的图的深度优先遍

30、历算法测试。以邻接矩阵表示的图的深度优先遍历算法测试。import ds_java.Graph1;public class Graph1_ex /图类的测试图类的测试 public static void main(String args) int mat1=0,1,0,1, /无向图无向图G6的邻接矩阵的邻接矩阵 1,0,1,1, 0,1,0,1, 1,1,1,0; Graph1 g1=new Graph1(mat1); g1.depthFirstSearch(); 对于无向图对于无向图G6，程序运行结果如下：，程序运行结果如下：深度优先遍历深度优先遍历Depth first search：

31、 v1 - v2 - v3 - v4 - v2 - v1 - v4 - v3 - v3 - v2 - v1 - v4 - v4 - v1 - v2 - v3 - 在一个含有在一个含有n个结点和个结点和e条边的图上进行深度优先遍历，对每个条边的图上进行深度优先遍历，对每个结点，结点，depthfs()方法至多被调用一次。因为一旦在一个结点上调用方法至多被调用一次。因为一旦在一个结点上调用depthfs()方法，便标志该结点方法，便标志该结点“已被访问已被访问”，此后便不再对该结点，此后便不再对该结点调用调用depthfs()方法。方法。3 以邻接表存储的图的深度优先遍历算法实现以邻接表存储的图的

32、深度优先遍历算法实现 在以邻接表存储的图在以邻接表存储的图Graph2类中，同样需要成员变量类中，同样需要成员变量visited数组和数组和n，所以，所以Graph2设计为继承设计为继承Graph1类。类。 构造方法中创建具有构造方法中创建具有n+1个元素的个元素的table数组，并将邻接矩数组，并将邻接矩阵阵mat中表示的边转换成邻接表中表示的边转换成邻接表table中的出边表。其中，中的出边表。其中，table0元素不用，使得结点序号元素不用，使得结点序号i与与table中的下标一致。中的下标一致。 output()方法输出邻接表方法输出邻接表table及其出边表的各个结点数据元及其出边表

33、的各个结点数据元素值。素值。depthfs()方法覆盖超类方法覆盖超类Graph1中的同名方法。中的同名方法。3以邻接表存储的图的深度优先遍历算法实现以邻接表存储的图的深度优先遍历算法实现import ds_java.OnelinkNode; /单向链表的结点类public class Graph2 extends Graph1 /以邻接表存储的图类 private OnelinkNode table; /图的邻接表 public Graph2(int mat) /以邻接矩阵建立图的邻接表 n=mat.length; /继承Graph1类的成员 table=new OnelinkNoden+1

34、; /建立结点表，多一个元素 OnelinkNode p=null,q; int i,j; for(i=1;i v2 nulltable2= v2 - v3 - v4 nulltable3= v3 nulltable4= v4 - v1 - v3 null深度优先遍历深度优先遍历Depth first search: v1 - v2 - v3 - v4 - v2 - v3 - v4 - v1 - v3 - v4 - v1 - v2 - v3 -1234567823 28 28 38 38 167 4567 145 【例题】用邻接表实现深度优先搜索【例题】用邻接表实现深度优先搜索例例:已知无向图

35、的邻接表如下已知无向图的邻接表如下,写出从顶点写出从顶点8出发的出发的DFS算法的顶点序列。算法的顶点序列。顶点序列顶点序列:DFSAL(8)DFSAL(4)DFSAL(2)DFSAL(1)DFSAL(3)DFSAL(6)84213756DFSAL(7)DFSAL(5)7.3.2 广度优先遍历广度优先遍历广度优先搜索（广度优先搜索（BFS）遍历是类似于树的）遍历是类似于树的层次遍历层次遍历的一种方法。的一种方法。v1v2v3v5v4v6v7v8只有父辈结点只有父辈结点被访问后才会被访问后才会访问子孙结点！访问子孙结点！把图人为的分层，把图人为的分层，按层遍历。按层遍历。1 广度优先遍历算法描述

36、广度优先遍历算法描述从图中选定的一个结点从图中选定的一个结点v0作为出发点，访问作为出发点，访问v0。 将访问过的结点将访问过的结点v0入队。入队。 当队列不空时，进入循环：当队列不空时，进入循环： 当队列空时，循环结束，说明从当队列空时，循环结束，说明从v0开始能够到达的所有结开始能够到达的所有结点都已被访问过。点都已被访问过。 广度优先搜索遍历类似于树的层次遍历。其中必须设立一个广度优先搜索遍历类似于树的层次遍历。其中必须设立一个队列来保存访问过的结点，算法描述如下：队列来保存访问过的结点，算法描述如下：u 有结点有结点vi出队。出队。u 访问与访问与vi有边相连的且未被访问过的所有结点有

37、边相连的且未被访问过的所有结点vj。u 访问过的结点访问过的结点vj入队。入队。v1v2v3v5v4v6v7v8过程分析过程分析广度优先搜索顺序广度优先搜索顺序: v1v2v3v4v5v6v7v8v1v2v3v4v5v6v7v8用队列实现用队列实现“广度优先搜索广度优先搜索”的图示的图示(1) ,将将vi 作为当前顶点作为当前顶点;(2)访问当前顶点的访问当前顶点的,并并将这些将这些邻接结点作当前顶点邻接结点作当前顶点;(3)重复步骤重复步骤(2) 直到图中直到图中都被访问。都被访问。队列的作用队列的作用:顶点被访问后入队顶点被访问后入队;队头出队访问其邻接点。队头出队访问其邻接点。队列队列Q

38、V0V1V2V3V4V5V6V7起始顶点起始顶点V0V1V2V7V3V4V5V6访问序列访问序列:出队顶点出队顶点:V0V0V1V2V1V3V4V2V5V6V3V7V4V5V6V72以邻接矩阵存储的图的广度优先遍历算法实现以邻接矩阵存储的图的广度优先遍历算法实现import ds_java.Queue2; /链式队列，元素类型为int public void breadthFirstSearch() /图的广度优先遍历 /k为起始结点序号 System.out.println(广度优先遍历Breadth first search:); for(int k=1;kv2-v4-v3- v2-v1-

39、v3-v4- v3-v2-v4-v1- v4-v1-v2-v3-3以邻接表存储的图的广度优先遍历算法实现以邻接表存储的图的广度优先遍历算法实现import ds_java.Queue2; /链式队列，元素类型为int public void breadthfs(int k) /图的广度优先遍历 /k为起始结点序号 int i,j=0; Queue2 q2=new Queue2(); /设置空队列 OnelinkNode p; i=k; System.out.print( v+k+ -); /访问起始结点 visitedi=1; /设置访问标记 q2.enqueue(i); /访问过的结点入队

40、while(!q2.isEmpty() /队列不空时 i=q2.dequeue(); /出队 if(tablei!=null) /查找有边相连的另一结点 对于有向图对于有向图G7，程序运行的结果如下：，程序运行的结果如下：广度优先遍历广度优先遍历Breadth first search: v1 -v2-v3-v4- v2 -v3-v4-v1- v3 - v4 -v1-v3-v2-书面作业书面作业:分别应用分别应用 DFS, BFS 实现遍历实现遍历 要求尽量按顶点序号顺序搜索要求尽量按顶点序号顺序搜索2154310861214715131191617181920上机作业上机作业: 建立一个图结

41、构，应用建立一个图结构，应用DFS或或BFS进行遍历。进行遍历。7.4 最小代价生成树最小代价生成树7.4.1 树与图树与图 连通的无回路的无向图称为无向树，简称树。诸连通分连通的无回路的无向图称为无向树，简称树。诸连通分量均为树的图称为森林，树是森林。量均为树的图称为森林，树是森林。 由于树中无回路，因此树中必定无自身环也无重边。若由于树中无回路，因此树中必定无自身环也无重边。若去掉树中的任意一条边，则树变为非连通图；若给树加上一去掉树中的任意一条边，则树变为非连通图；若给树加上一条边，则形成图中的一条回路。条边，则形成图中的一条回路。7.4.2 生成树生成树1. 生成树的定义生成树的定义

42、如果图如果图T是无向图是无向图G的生成子图，且的生成子图，且T是树，则图是树，则图T称为图称为图G的的生生成树成树。图。图G的生成树的生成树T包含包含G中的所有结点和尽可能少的边。中的所有结点和尽可能少的边。 设图设图G=(V,E)是一个连通的无向图，从是一个连通的无向图，从G中的任意一个结点中的任意一个结点v0出出发进行一次遍历所经过的边的集合为发进行一次遍历所经过的边的集合为TE，则，则T=(V,TE)是是G的一个的一个连通子图，即得到连通子图，即得到G的一棵生成树。的一棵生成树。7.4.2 生成树生成树利用利用 DFS 或或 BFS 获取获取生成树生成树例，例，DFSv1v2v3v5v4

43、v6v7v8v1v2v3v4v6v8v5v7DFS生成树生成树例，例，BFSv1v2v3v5v4v6v7v8BFS生成树生成树v1v2v3v4v5v6v7v87.4.3 最小代价生成树最小代价生成树一个无向图可以对应多个生成树。一个无向图可以对应多个生成树。一个带权无向图一个带权无向图(无向网无向网)同样可以对应多个生成树。同样可以对应多个生成树。一棵一棵生成树的代价生成树的代价定义为树上各边的权值总和。定义为树上各边的权值总和。如何求取如何求取最小生成树最小生成树？代价最小的生成树称为代价最小的生成树称为最小生成树最小生成树。实际价值？实际价值？v1v2v3v5v4v61556536642v

44、1v2v3v5v4v615342生成树生成树v1v2v3v5v4v653642欲在欲在n n个城市间建立通信网，则个城市间建立通信网，则n n个城市应铺个城市应铺n-1n-1条线路；但因为每条线路条线路；但因为每条线路都会有对应的经济成本，而都会有对应的经济成本，而n n个城市可能有个城市可能有n(n-1)/2 n(n-1)/2 条线路，那么，条线路，那么，如何选择如何选择n1n1条线路使总费用最少？条线路使总费用最少？典型用途：典型用途：先建立数学模型：先建立数学模型：顶点顶点表示城市，有表示城市，有n n个；个；边边表示线路，有表示线路，有n1n1条；条；边的权值边的权值表示线路的经济代价

45、；表示线路的经济代价；连通网连通网表示表示n n个城市间的通信网。个城市间的通信网。显然此连通网是一显然此连通网是一棵棵生成树！生成树！问题抽象：问题抽象： n n个顶点的生成树很多，需要从中选一棵个顶点的生成树很多，需要从中选一棵代价最小代价最小的生成树，的生成树，即该树即该树各边的代价之和各边的代价之和最小。此树便称为最小生成树最小。此树便称为最小生成树MSTMST。7.4.3 最小代价生成树最小代价生成树 按照生成树的定义，按照生成树的定义，n个结点的连通图的生成树有个结点的连通图的生成树有n个结点个结点n-1条边。因此，构造最小生成树的准则有条边。因此，构造最小生成树的准则有3条：条：

46、 必须只使用该图中的边来构造最小生成树。必须只使用该图中的边来构造最小生成树。 必须使用且仅使用必须使用且仅使用n-1条边来连接图中的条边来连接图中的n个结点。个结点。不能使用产生回路的边。不能使用产生回路的边。7.4.3 最小代价生成树最小代价生成树 设连通带权图设连通带权图G=(V,E)有有n个结点和个结点和m条边。最初先构造一个包条边。最初先构造一个包括全部括全部n个结点和个结点和0条边的森林条边的森林T=T1,T2,TN，以后每一步向，以后每一步向T中中加入一条边，它应当是一端在加入一条边，它应当是一端在T的某一棵树的某一棵树Ti上、而另一端不在上、而另一端不在Ti上的所有边中具有最小

47、权值的边。由于边的加入，使上的所有边中具有最小权值的边。由于边的加入，使T中的某两中的某两棵树合并为一棵，树的棵数减棵树合并为一棵，树的棵数减1。经过。经过n-1步，最终得到一棵有步，最终得到一棵有n-1条边的最小代价生成树。条边的最小代价生成树。求求MSTMST有多种算法，但最常用的是以下两种：有多种算法，但最常用的是以下两种：vKruskalKruskal（克鲁斯卡尔）算法（克鲁斯卡尔）算法vPrimPrim（普里姆）算法（普里姆）算法 KruskalKruskal算法特点：算法特点：将边归并将边归并，适于求边，适于求边稀疏的网稀疏的网的最小生成树。的最小生成树。PrimPrim算法特点算

48、法特点: : 将顶点归并将顶点归并，与边数无关，适于，与边数无关，适于边稠密的网边稠密的网。对边操作对边操作对顶点操作对顶点操作Kruskal 算法算法思想：思想：重复执行重复执行:N = ( V , E ) 是是 n 顶点的连通网，设顶点的连通网，设 E 是连通网中边的集合；是连通网中边的集合； 选取选取 E 中权值最小的边中权值最小的边 ( u , v ) ，否，否，将边将边 ( u , v ) 纳入纳入 TE 中，并从中，并从 E 中删除边中删除边 ( u , v ) ；判断边判断边 ( u , v ) 与与 TE 中的边是否构成回路中的边是否构成回路 ？直至直至 E 为空为空 ；构造最

49、小生成树构造最小生成树 N = ( V , TE )，TE 是最小生成树中边的集合，是最小生成树中边的集合，初始初始 TE = ；u 和和 v 一定一定不在同一个不在同一个连通分量中连通分量中v1v2v3v5v4v61556536642例，例，v1v2v3v5v4v615342初始初始 TE = 当前权值最小边当前权值最小边 ( v1 , v3 )当前权值最小边当前权值最小边 ( v4 , v6 )当前权值最小边当前权值最小边 ( v2 , v5 )当前权值最小边当前权值最小边 ( v3 , v6 )当前权值最小边当前权值最小边 ( v1 , v4 )当前权值最小边当前权值最小边 ( v3 ,

50、 v4 )当前权值最小边当前权值最小边 ( v2 , v3 )当前权值最小边当前权值最小边 ( v1 , v2 )当前权值最小边当前权值最小边 ( v3 , v5 )当前权值最小边当前权值最小边 ( v5 , v6 )Prim 算法算法思想：思想：重复执行重复执行:N = ( V , E ) 是具有是具有 n 个顶点的连通网，设个顶点的连通网，设 U 是最小生成树中顶点的是最小生成树中顶点的集合，设集合，设 TE 是最小生成树中边的集合；是最小生成树中边的集合； 初始，初始，U = u1 ，TE = ，在所有在所有 uU，vV- -U 的边的边 ( u , v ) 中寻找代价中寻找代价最小最小

51、的边的边( u , v ) ，并纳入集合并纳入集合 TE 中；中；同时将同时将 v 纳入集合纳入集合 U 中；中；直至直至 U = V 为止。为止。集合集合 TE 中必有中必有 n- -1 条边。条边。 v1v2v3v5v4v61556536642例，例，v1v31v25v53v64v42初始初始: U = v1 ，V- -U = v2 , v3 , v4 , v5 , v6 TE = U = v1 , v3 ，V- -U = v2 , v4 , v5 , v6 U = v1 , v3 , v6 ，V- -U = v2 , v4 , v5 重点重点: 边一定存在于边一定存在于 U 与与 V-

52、-U 之间。之间。U = v1 , v3 , v4 , v6 ，V- -U = v2 , v5 U = v1 , v2 , v3 , v4 , v6 ，V- -U = v5 U = v1 , v2 , v3 , v4 , v5 , v6 ，V- -U = 算法算法:初始化，初始化，U = v1 ，TE = ；寻求权值最小边寻求权值最小边 ( u , v )，满足，满足 uU & vV- -U；/循环循环TE = TE + ；U = U + v ；记录记录 v1 到其它各顶点的权值；到其它各顶点的权值； /循环循环记录新顶点记录新顶点 v 到其它各顶点的权值；到其它各顶点的权值； /循环

53、循环while ( U != V ) return OK ;2. 构造最小生成树构造最小生成树 要求：写中间过程要求：写中间过程1245631651062111143318197.5 最短路径最短路径兰州兰州太原太原北京北京济南济南徐州徐州郑州郑州西安西安旅客希望停靠站越少越好，则应选择旅客希望停靠站越少越好，则应选择济南济南北京北京太原太原兰州兰州旅客考虑的是旅程越短越好，则应选择旅客考虑的是旅程越短越好，则应选择1120920720210540340640190济南济南徐州徐州郑州郑州西安西安兰州兰州7.5 7.5 最短路径最短路径典型用途：典型用途：交通问题。如：城市交通问题。如：城市A

54、 A到城市到城市B B有多条线路，但每条线路的交有多条线路，但每条线路的交通费（或所需时间）不同，那么，通费（或所需时间）不同，那么，如何选择一条线路，使总费用（或总如何选择一条线路，使总费用（或总时间）最少？时间）最少？问题抽象：问题抽象：在在带权有向图带权有向图中中A A点（源点）到达点（源点）到达B B点（终点）的多条路径中，点（终点）的多条路径中，寻找一条寻找一条各边权值之和最小各边权值之和最小的路径，即最短路径。的路径，即最短路径。（注：最短路径与最小生成树不同，路径上不一定包含（注：最短路径与最小生成树不同，路径上不一定包含n n个顶点）个顶点）两种常见的最短路径问题：两种常见的最

55、短路径问题：一、一、 单源最短路径单源最短路径用用Dijkstra（迪杰斯特拉）（迪杰斯特拉）算法算法二、所有顶点间的最短路径二、所有顶点间的最短路径用用Floyd（弗洛伊德）算法（弗洛伊德）算法一顶点到其一顶点到其余各顶点余各顶点任意两顶任意两顶点之间点之间7.5.1 从单个源点到其余各顶点的最短路径算法从单个源点到其余各顶点的最短路径算法 Dijkstra 算法算法思想思想: 利用已得到的顶点的最短路径来计算其它顶点的最短路径。利用已得到的顶点的最短路径来计算其它顶点的最短路径。贪心算法贪心算法: 利用局部最优来计算全局最优。利用局部最优来计算全局最优。例，例，v5v0v1v4v36010

56、05v21030201050求从求从 v0 到其余各顶点的最短路径。到其余各顶点的最短路径。1. 初始，初始，Di 的值为的值为 v0 到到 vi 的弧的权值的弧的权值Di 表示表示 v0 到到 vi 的最短路径的长度的最短路径的长度显然，显然，Di 中的最小值中的最小值 D2 便是便是 v0到到 v2 的最短路径的长度，的最短路径的长度，Path2=( v0 , v2 )Pathi表示表示v0 到到 vi 的最短路径上的顶点的最短路径上的顶点V1 V2 V3 V4 V5V0Di10301002. 如何寻找下一条最短路径？如何寻找下一条最短路径？例，例，v5v0v1v4v3601005v210

57、30201050设下一条最短路径的终点是设下一条最短路径的终点是 vj ，则，则这条最短路径或者是这条最短路径或者是 ( v0 , vj ) 、或、或者是者是 v0 经过经过 v2 到达到达 vj 的路径的路径 ；其中取其中取 Di(D2除外除外) 中的最小值得中的最小值得到到 v4，Path4=( v0 , v4 ) 。3. 如何寻找下一条最短路径？如何寻找下一条最短路径？V1 V2 V3 V4 V5V0Di106030100算法描述算法描述假设用假设用带权的邻接矩阵带权的邻接矩阵 arcsij 来表示带权有向图。来表示带权有向图。初始，初始，Di 存放存放 v0 到到 vi 各顶点的弧的权

58、值，各顶点的弧的权值，Di=arcs0i ，S=；利用公式利用公式 Dj = Min Di | | viV- -S 得到一条新的从得到一条新的从 v0 出发出发的最短路径及新的终点的最短路径及新的终点 vj ，令，令 S = S + vj ；利用利用 vj 修改从修改从 v0 出发到集合出发到集合 V- -S 中任一顶点中任一顶点 vk 可达的路径的长度可达的路径的长度 ；Dj + arcsjk 与与 Dk算法时间复杂度算法时间复杂度: O(n2)利用已得到的顶点的最短路径来修改得到其它顶点的更短路径。利用已得到的顶点的最短路径来修改得到其它顶点的更短路径。重复执行重复执行 n- -1 遍，每

59、遍求出一条新的最短路径遍，每遍求出一条新的最短路径例，例，v5v0v1v4v3601005v21030201050带权邻接矩阵带权邻接矩阵 10 30 1000 1 2 3 4 5 5 50 10 20 60 012345v21030100v0v2v2106030100v0v4v430v2 , v450 90v0v4v3v350v2 , v4 , v3 60v0v4v3v5v560v2 , v4 , v3 , v5 v1v1v2v3v4v5最短路径最短路径新顶点新顶点S顶点顶点路径长度路径长度每次修改都用每次修改都用的是最新加入的是最新加入集合集合 S 的顶点的顶点7.5.2 每一对顶点之间的

60、最短路径算法每一对顶点之间的最短路径算法 Floyd 算法算法算法算法1: 每次以一个顶点为源头，重复执行每次以一个顶点为源头，重复执行 Dijkstra 算法算法 n 遍，便遍，便可得到每一对顶点之间的最短路径。可得到每一对顶点之间的最短路径。算法时间复杂度算法时间复杂度: O(n3)算法算法2: Floyd 算法算法算法时间复杂度算法时间复杂度: O(n3)Floyd 算法思想算法思想初始初始，从图的，从图的带权邻接矩阵带权邻接矩阵 D(- -1) 出发，作为顶点出发，作为顶点 vi 到到 vj 的最短路径。的最短路径。0. 考虑经过考虑经过 v0 是否会存在更短的路径，即是否会存在更短的路径，即