第二章静电场中的导体和电介质

1、第二章第二章 静电场中的导体和电介质静电场中的导体和电介质 1 1 静电场中的导体静电场中的导体2 2 电容和电容器电容和电容器3 3 电介质电介质4 4 介质中静电场能量密度介质中静电场能量密度1.1.静电平衡静电平衡 导体内部和表面无自由电荷的定向移动，导体内部和表面无自由电荷的定向移动，电场不随时间变化。该状态下，导体处于静电场不随时间变化。该状态下，导体处于静电平衡状态。电平衡状态。0内E在一定温度下，自由在一定温度下，自由电子作无规热运动电子作无规热运动1 1 静电场中的导体静电场中的导体 2.2.均匀导体静电平衡的条件均匀导体静电平衡的条件一一. .导体的静电平衡条件导体的静电平衡

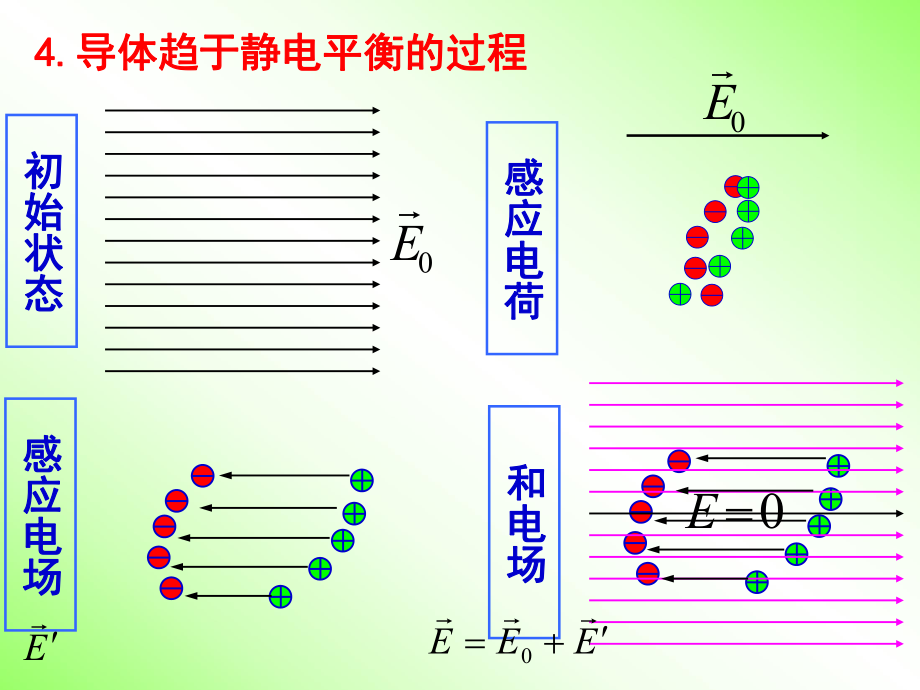
2、条件3.3.导体静电平衡的条件证明导体静电平衡的条件证明必要条件必要条件图示说明图示说明0E文字说明文字说明导体内导体内E不处处为不处处为0 0自由电荷受力运动自由电荷受力运动电场随时间变化电场随时间变化不平衡不平衡充分充分条件证明见本节附录条件证明见本节附录B B 0E4.4.导体趋于静电平衡的过程导体趋于静电平衡的过程初始状态初始状态感应电荷感应电荷0E感应电场感应电场E0E和电场和电场EEE05.5.导体静电平衡时的性质导体静电平衡时的性质导体外表面附近的导体外表面附近的场强处处与表面场强处处与表面垂直垂直。-电力线与等位面电力线与等位面处处正交处处正交导体内部电场为零导体内部电场为零导

3、体是导体是等位体等位体, ,导体表面是导体表面是等位面等位面0QPPQl dEU内PQQP0内E二二. .静电平衡导体的电荷分布静电平衡导体的电荷分布 由导体的静电平衡条件和静电场的基本由导体的静电平衡条件和静电场的基本性质，可以得出导体上的电荷分布。性质，可以得出导体上的电荷分布。1.1.体内无净电荷，电荷只分布在表面体内无净电荷，电荷只分布在表面0SSdEqdViiV0 0证明：在导体内任取体积元证明：在导体内任取体积元dV由高斯定理由高斯定理体积元任取体积元任取证毕证毕0内EdV导体带电只能在表面！导体带电只能在表面！2.2.导体表面电荷与外部表面场强的关系导体表面电荷与外部表面场强的关

4、系),(zyx),(zyxE表SSdEdSSdSSdESdE表dSE表0dS0表E设导体表面电荷面密度为设导体表面电荷面密度为相应的电场强度为相应的电场强度为设设P是导体外紧靠导体表面的一点是导体外紧靠导体表面的一点n ：外法线方向外法线方向nE0表写作写作导体导体Psd在表面凸出的在表面凸出的尖锐部分尖锐部分( (曲率曲率是正值且较大是正值且较大) )， 较大较大，3.3.孤立带电导体表面电荷分布孤立带电导体表面电荷分布一般情况一般情况较复杂；较复杂；孤立孤立的带电导体，电荷分布的带电导体，电荷分布有定性规律。有定性规律。孤立带电导体球孤立带电导体球 表面等曲率表面等曲率C在比较在比较平坦部

5、分平坦部分( (曲率较小曲率较小) ) 小小，在，在表面表面凹进部分凹进部分( (曲率为负曲率为负) ) 最小最小。非孤立导体的面电荷分布非孤立导体的面电荷分布q最大曲率处，最大曲率处，面电荷密度低面电荷密度低孤立导体外表面场强与曲率的关系孤立导体外表面场强与曲率的关系曲率曲率 面电荷密度面电荷密度电场强度电场强度气体击穿放电气体击穿放电 尖端放电尖端放电高高E, 加速加速空气中的电子空气中的电子AA+A*孤立导体孤立导体E电离电离hAA*电晕光电晕光尖端放电一例尖端放电一例尖端放电的防止与应用尖端放电的防止与应用高压输电线的电晕（防止）高压输电线的电晕（防止）避雷针（利用）避雷针（利用）空气

6、负离子发生器（利用）空气负离子发生器（利用） 负离子形成：负离子形成：e+A- Ae+A- A- - 负离子作用：空气维生素负离子作用：空气维生素 臭氧发生器：臭氧用处臭氧发生器：臭氧用处杀菌、水处理杀菌、水处理电子打火机电子打火机电晕除尘电晕除尘静电印刷静电印刷三三. . 导体壳与静电屏蔽导体壳与静电屏蔽腔内腔内腔外腔外讨论的问题是：讨论的问题是：1)1)腔内、外表面电荷分布特征腔内、外表面电荷分布特征2)2)腔内、腔外空间电场特征腔内、腔外空间电场特征导体壳的导体壳的几何结构几何结构腔内、腔外腔内、腔外内表面、外表面内表面、外表面内表面内表面外表面外表面 内表面处处没有电荷，电荷只分布在外

7、表面。内表面处处没有电荷，电荷只分布在外表面。 腔内场强为零，或腔内场强为零，或腔内电势处处相等。腔内电势处处相等。1.1.腔内无带电体腔内无带电体基本性质：基本性质：证明证明: :0SsdE0iiq在导体壳内作高斯面在导体壳内作高斯面S高斯定理高斯定理0内表面Q 内表面一部分带正电荷，一部分带负电荷内表面一部分带正电荷，一部分带负电荷 内表面处处没有电荷内表面处处没有电荷与等势矛盾与等势矛盾则会从正电则会从正电荷向负电荷荷向负电荷发出电力线发出电力线两性质两性质得证得证两种情况两种情况S+？2.2.腔内有带电体腔内有带电体表达式表达式腔内电场严腔内电场严格计算困难格计算困难qQ表面腔内用高斯

8、定用高斯定理可证理可证1)1)与电量与电量 有关；有关；q2)2)与腔内带电体、几何与腔内带电体、几何因素、介质有关。因素、介质有关。定定性性结结论论基本性质：基本性质：导体壳内表面所带电荷与腔导体壳内表面所带电荷与腔内电荷的代数和为零。内电荷的代数和为零。S q3.3.静电屏蔽的装置静电屏蔽的装置-接地导体壳接地导体壳qQ外表面外表面=qQ内表面内表面=-q导体壳接地，腔外表面电荷流向导体壳接地，腔外表面电荷流向地，导体与外界等势，无电力线地，导体与外界等势，无电力线穿出，对腔外场无影响。穿出，对腔外场无影响。q不接地，腔内不接地，腔内电荷对腔外场电荷对腔外场有影响。有影响。接地对导体壳屏蔽

9、特性的影响接地对导体壳屏蔽特性的影响腔内场腔内场腔外场腔外场只与只与内部带电量、内部几何条件及介质内部带电量、内部几何条件及介质有关。即，在腔内：有关。即，在腔内：E外带电体外带电体+ E E外表面外表面=0=0只与只与外部带电量、外部几何条件及介质外部带电量、外部几何条件及介质有关。即，在腔外：有关。即，在腔外：E内带电体内带电体+ E E内表面内表面=0=0讨论讨论接地影响接地影响影响腔影响腔外表面的电荷，由此影响外部电场外表面的电荷，由此影响外部电场实际应用中的静电屏蔽实际应用中的静电屏蔽两种不同形式两种不同形式（1 1）外部静电对测量仪器的影响）外部静电对测量仪器的影响屏蔽方法：屏蔽方

10、法：（2 2）静电干扰源静电干扰源对外部环境的影响对外部环境的影响屏蔽方法：屏蔽方法：测量仪器测量仪器外部静外部静电干扰电干扰金属屏蔽金属屏蔽静电干扰源静电干扰源金属屏蔽金属屏蔽接地？接地？板板oror网网良好的地良好的地要接地要接地例例1 1 在无限大带电平面的电场中，在无限大带电平面的电场中，平行放置一无限大金属平板平行放置一无限大金属平板 求：金属板两面电荷面密度求：金属板两面电荷面密度21，P21022202010211212解解: :设金属板面电荷密度设金属板面电荷密度21由对称性和电量守恒由对称性和电量守恒导体体内任一点导体体内任一点P P场强为零场强为零x02012022例例2

11、2 金属球金属球A与与金属球壳金属球壳B同心同心放置放置求求:1):1)电量分布电量分布qQ已知：球已知：球A半径为半径为0R，带电为，带电为金属壳金属壳B内外半径分别为内外半径分别为21RR，带电为带电为AUBU2)2)球球A和壳和壳B的电位的电位QABo0Rq1R2R解：解：1)1)导体电荷分布在表面上导体电荷分布在表面上球球A的电量只可能在球的表面的电量只可能在球的表面壳壳B有两个表面有两个表面 电量可能分布在电量可能分布在内内、外外两个两个表面表面由于由于A、B同心放置，同心放置，仍维持球对称仍维持球对称 电量在表面均匀分布电量在表面均匀分布QABo0Rq1R2RqqQQB外球球A均匀

12、分布着电量均匀分布着电量qQB内由高斯定理和电量守恒由高斯定理和电量守恒可以证明壳可以证明壳B的电量分布是的电量分布是qqQ相当于均匀带电的球面相当于均匀带电的球面相当于一个均匀带电的球面相当于一个均匀带电的球面ABq0 qQB内证明壳证明壳B上电量的分布：上电量的分布：在在B内紧贴内表面作高斯面内紧贴内表面作高斯面qQQB外0SsdE0iiqS面面S的电通量的电通量高斯定理高斯定理电荷守电荷守恒定律恒定律qQB内qqQABqS由由高斯定理求出各空高斯定理求出各空 间区域的电场强度间区域的电场强度求带电球电位求带电球电位E0210,RrRRr204rq10RrR204rqQ2Rr 由电位定义由

13、电位定义0RAldEUqQ o0Rq1R2R-q204RqQ22110RRRRRdrEdrEdrE2204RRBrqQdrEU21000404RRRrqQrq201000444RqQRqRqUAqQ o0Rq1R2R-q例例3 3 接地导体球附近有一点电荷接地导体球附近有一点电荷, ,如图所示。如图所示。求求: :导体上感应电荷的电量导体上感应电荷的电量解解: : 接地，即接地，即由于导体是个等势体由于导体是个等势体O O 点的电势为零，则点的电势为零，则04400lqRQqlRQ0UQ设设: :感应电量为感应电量为lqRO O一一. .孤立导体的电容孤立导体的电容孤立导体的定义孤立导体的定义

14、孤立导体电量、电位之间的关系孤立导体电量、电位之间的关系孤立导孤立导体带电体带电产生电场产生电场对应电位对应电位表面l dEU球形：球形：RQU04正比关系正比关系QU 2 2 电容及电容器电容及电容器电容只与几何因素和介质有关电容只与几何因素和介质有关与带电量、电位无关与带电量、电位无关是带电体是带电体固有固有的容电本领的容电本领单位单位: :法拉法拉FUQC定义定义对于任意孤立导体：对于任意孤立导体： U、Q之间的之间的正比关系正比关系仍然成立仍然成立意义意义每升高每升高单位电位单位电位所需要的所需要的电量电量 说明说明041Rm9109ER310例例 求真空中孤立导体球的电容求真空中孤立

15、导体球的电容( (如图如图) )RQU04UQCQ设球带电为设球带电为R解解：导体球电势导体球电势导体球电容导体球电容R04介质介质几何几何问题问题F1欲得到欲得到 的电容的电容?孤立导体球的半径孤立导体球的半径R由孤立导体球电容公式知由孤立导体球电容公式知法拉单位过大法拉单位过大常用单位常用单位:FF6100 . 11FpF12100 . 11二二. .导体组的电容导体组的电容由静电屏蔽由静电屏蔽: :导体壳内部的场只由腔内的电量导体壳内部的场只由腔内的电量和几何条件及介质决定和几何条件及介质决定ABABABUQC定义：定义：qAqAq内表面内表面常用的电容器典型的电容器典型的电容器平行板平

16、行板d球形球形21RR柱形柱形1R2R高斯高斯+ 匀匀高斯高斯r r 地有地有 2ABARRR积积 24AR高斯高斯r r 三、三、电容器储能电容器储能电容器的能量电容器的能量表现表现例子：照相机闪光灯例子：照相机闪光灯能量形式及转化能量形式及转化电容器放电时，负电荷由低电位到高电位，电场力做正功。静电能转化为其他形式(光能等)电容器静电能来源？ 能将电子由电容器正电极搬运至负电极的 充电电源电容器能量表达式推导电容器充电时，在充电电源的作用下，电场从电容器正极到达负极搬运电量为-dq的电子，对应的电位能增加为电子流U-U+)(UUdqdWedqCqUdqUUdq)(充电结束时，电容 器的电能

17、为： dqCqdWWQWeee00CQ221CUQ 221CU3 3 电介质电介质一、电介质的极化一、电介质的极化1 1、电介质、电介质电介质就是绝缘体。电介质就是绝缘体。2 2、极化现象、极化现象现象：实验告知：现象：实验告知： ，如何解释成因？，如何解释成因？0UU +Q -Q +Q -Q Uo U 1 1、电介质的分类、电介质的分类 无极分子无极分子电介质分子的正、负电荷电介质分子的正、负电荷中心在没有外场时重合。中心在没有外场时重合。有极分子有极分子电介质分子正、负电荷中电介质分子正、负电荷中心在没有外场时不重合。心在没有外场时不重合。形成电偶极矩，叫分子的形成电偶极矩，叫分子的固有电

18、矩。固有电矩。二、极化的微观机制二、极化的微观机制0E0E0E加0E0E分p2 2、电介质极化的分类、电介质极化的分类 (1) (1) 无极分子的位移极化无极分子的位移极化分p无极分子在外场中的感生电矩无极分子在外场中的感生电矩极化电荷极化电荷(束缚电荷束缚电荷) (2) (2) 有极分子的取向极化有极分子的取向极化无序无序 有序，有序， 0E场各向同性各向同性 取向极化。取向极化。极化电荷极化电荷(束缚电荷束缚电荷)排列愈有序说明极化愈强，排列愈有序说明极化愈强， 定量描述：定量描述：3.3.描述极化程度的物理量描述极化程度的物理量-极化强度矢量极化强度矢量PVpPiiV分子0lim定义定义

19、2mcSI 单位单位ip分子单个分子的单个分子的电偶极矩电偶极矩 定义定义P0Vp分子处于极化状态时处于极化状态时 V体积元体积元 ：V宏观上无限小宏观上无限小微观上无限大微观上无限大电荷面密度( )单位 单位体积内的分子电矩之和 三三. .极化强度极化强度 与极化电荷分布的关系与极化电荷分布的关系P 以均匀极化为例，说明极化电荷分布与极化强度矢量的关系。以均匀极化为例，说明极化电荷分布与极化强度矢量的关系。q电电nl 若介质均匀，穿出和穿入的极化电荷数应相等，若介质均匀，穿出和穿入的极化电荷数应相等，体内不会有净电荷，即极化电荷的体密度为零。体内不会有净电荷，即极化电荷的体密度为零。2 2、

20、电介质表面极化电荷面密度、电介质表面极化电荷面密度由前面，通过由前面，通过 dS 面元的总束缚电荷为面元的总束缚电荷为若若 dS 面刚好在介质表面，面刚好在介质表面，则则 dq 就是因极化而在介就是因极化而在介质表面质表面 dS 面积上显露出面积上显露出的面束缚电荷，则的面束缚电荷，则Pcos e /2, e 0 /2, e 0 解解 例例1,1,均匀极化介质球面上极化电荷的分布。均匀极化介质球面上极化电荷的分布。电极化强度为电极化强度为 。Pn xzyoj取球坐标系取球坐标系, ,球心球心o o为原点为原点, ,P 与与z轴平行。轴平行。PA取球面上任意一点取球面上任意一点A。该点的单位面元

21、矢量该点的单位面元矢量为为 , ,n 其方位角如图所示。其方位角如图所示。cosPnP/200/2-/2P+ 0四、退极化场四、退极化场 + +介质介质0E极化电荷极化电荷EEEE0 与与 方向方向0E介质存在时的总电场介质存在时的总电场EE0E(a)(a)介质外部介质外部(b)(b)介质内部介质内部 某些区域：方向大致相同某些区域：方向大致相同某些区域：方向大致相反某些区域：方向大致相反总是大致相反总是大致相反 总是削弱总是削弱E0E 极化电荷产生的电场极化电荷产生的电场 被称为被称为退退极化场极化场E解解: :均匀介质内部的极化电荷为零均匀介质内部的极化电荷为零, ,极化极化电荷仅在表面出

22、现。电荷仅在表面出现。例例1 1 已知极化强度已知极化强度 ，求平行板电容器中均，求平行板电容器中均匀电介质板内的退极化场。匀电介质板内的退极化场。PPn左侧介质面：左侧介质面：PPnPcos1n右侧介质面：右侧介质面：P200002012222PPPE1E2E极化电荷在板内的电场方向相同，由叠加定理得：极化电荷在板内的电场方向相同，由叠加定理得：方向与原方向与原外场相反外场相反例例2 2 已知极化强度为已知极化强度为 ，求均匀极化的电介，求均匀极化的电介质球在球心的退极化场。质球在球心的退极化场。P: : 取球坐标系，取球坐标系，z z轴沿极化方向。轴沿极化方向。解解jddRdSsin2co

23、sPe则极化电荷分布为：则极化电荷分布为：由对称性，球心由对称性，球心O点场强只点场强只有有z分量。分量。在球面上取过在球面上取过A点的面元点的面元dS ,n xzyoP1Ed A对应的极化电荷元：对应的极化电荷元：dSPdSqdecosjddPsincos40n xzyoP1Ed A2041RqddEqd 在在O点产生的场强为：点产生的场强为：z 轴分量为：轴分量为：jddP EdEdzsincos4)cos(20整个球面在球心整个球面在球心O O点产生的退极化场：点产生的退极化场：0200203sincos4jPddPEdEEzz球面“-”“-”代表电代表电场沿负场沿负z z方向。方向。

24、五五. .电介质的极化规律电介质的极化规律 极化率极化率2.2.各向同性线性电介质的极化规律各向同性线性电介质的极化规律EPe0称为极化率（无量纲的纯数）称为极化率（无量纲的纯数）e1.1.电介质的极化规律定义电介质的极化规律定义 与总电场与总电场 之间的关系，一般较复杂。之间的关系，一般较复杂。 PE在在一般介质中：一般介质中： 、 不一定在同一方向不一定在同一方向PE 随随 变化变化eE本节本节仅仅讨论：讨论：各向同性各向同性/ /线性电线性电介质介质总电场总电场 EPe退极化场退极化场 EEPEe、互相影响、制约互相影响、制约六六. .电位移矢量电位移矢量D有电介质时的高斯定理有电介质时

25、的高斯定理能否省去介质极化电荷能否省去介质极化电荷 、电场、电场 的分析？直接求的分析？直接求 。)(E E解决方法：解决方法： 引入电位移矢量引入电位移矢量D分析：分析：高斯定理是关于高斯定理是关于电荷电荷与与电场通量电场通量之间的关系，之间的关系，由库仑推导得到。当介质存在时，计入极化电由库仑推导得到。当介质存在时，计入极化电荷，以及对应电场，高斯定理应该荷，以及对应电场，高斯定理应该仍然成立仍然成立： 有电介质时的高斯定理有电介质时的高斯定理问题：问题：有介质时的高斯定理的推导：有介质时的高斯定理的推导：SSqqSdE)(100SSSqSdPSdE00SSqSdD0SSoSqqSdE0S

26、oSqSdPE)(0定义定义PED0有介质时的高斯定理有介质时的高斯定理消去极化电荷消去极化电荷电位移矢量电位移矢量DEP0量纲量纲: : PD单位单位 C/mC/m在各向同性线性介质中在各向同性线性介质中EPe0EE EEDee0000)1(= 电介质的相对介电常数，电介质的相对介电常数，无量纲，真空中无量纲，真空中 = 1。ED0介质方程介质方程)(qorPED即即: :说明说明SSqSdD0自由电荷自由电荷公式优点公式优点在具有某种对称性的情况下，可以在具有某种对称性的情况下，可以首先由高斯定理出发，直接解出首先由高斯定理出发，直接解出 （无需极化电荷、电场分析），继（无需极化电荷、电场

27、分析），继而求解其他物理量。而求解其他物理量。 D七七. .利用介质中的高斯定理解题利用介质中的高斯定理解题求求: :板内的板内的 E、P。0例例1 1 平行板电容器，板上自由电荷面密度为平行板电容器，板上自由电荷面密度为充满相对介电常数为充满相对介电常数为 的均匀各的均匀各向同性线性电介质。向同性线性电介质。解解: : 分析分析D,E取高斯面取高斯面000ED介质内两侧面金属内SdDSdDSdDSdDS=0=0=0=000000EDEDSqDS00极化强度：极化强度：EEPe00) 1(介质表面极化电荷面密度：介质表面极化电荷面密度：000EDPnP例例2.2.整个空间充满介电常数为整个空间

28、充满介电常数为 的电介质，其中有的电介质，其中有一点电荷一点电荷 q0，求场强分布。，求场强分布。 q0S解：取以解：取以qo为中心，半径为中心，半径 r 的球的球形高斯面形高斯面S，由对称性，由对称性，S上上任一点任一点 D 的方向与的方向与S垂直，垂直，由高斯定理。由高斯定理。024qDrSdDS204 rqD ED 0qrqDE真空中点电真空中点电荷场强荷场强 E0例例3 3 如图示，导体球置于均匀如图示，导体球置于均匀各向同性介质中各向同性介质中 求：求：1.1.场的分布场的分布2.2.紧贴导体球表面处的极化电荷紧贴导体球表面处的极化电荷3.3.两介质交界处的

29、极化电荷两介质交界处的极化电荷1121R2R0R解：解：1)1)场的分布场的分布01E01P0P导体内部导体内部0Rr 1内内10RrR rrQE42102rrQP412101022内内21RrR rrQE4204 1122)2)求紧贴导体球表面处的极化电荷求紧贴导体球表面处的极化电荷141201RQ204 Rq Q111PnP0Rr 3)3)两介质交界处极化电荷两介质交界处极化电荷112n PnPPnPnPnPnP)(2121221121n1n2P1,2n 0EE普遍结论普遍结论? ?问题问题（1）成立条件（只掌握，不证明）成立条件（只掌握，不证明） 均匀介质充满电场所在空间均匀介质表面为等

30、位面aRrd1200ED00ED 连续变化，但连续变化，但 的等值面处处与等势面重合。的等值面处处与等势面重合。 问题问题（2）均 匀均 匀 电 介 质 内 ， 无 自 由 电 荷电 介 质 内 ， 无 自 由 电 荷（q0=0）时，内部为什么没有极）时，内部为什么没有极化电荷化电荷 ? ? )0(q00内SSqSdDEEPe100DE01DP1SSSdDSdPq101SSdD均匀均匀介质介质问题问题（3）非均匀非均匀电介质内，均匀外电场时，电介质内，均匀外电场时，内部存在极化电荷内部存在极化电荷 ? ?x1x2x1221SSSSdDSdDSdDSdD两侧面0E1SS2S002211qSDSD

31、(?)0021EDD12121211SqP dSDDS SE 002112120210)(021均匀介质例例4.4.如图，两块靠近的平行金属板原为真空。使它们分别带如图，两块靠近的平行金属板原为真空。使它们分别带上等量异号电荷，面密度上等量异号电荷，面密度 0 0，板间电压，板间电压U0。保持电量不变将。保持电量不变将极板一半充以介电常数极板一半充以介电常数 的电介质，求极板电压的电介质，求极板电压U，介质表，介质表面束缚电荷面密度？面束缚电荷面密度？+E1D1E2D2+ 1 1 2+ 2解：解： 未充介质前，未充介质前，000E0000ddEU充介质后，不考虑边缘效应，则充介质后，不考虑边缘

32、效应，则 E、D垂直极板并垂直极板并在两半部分内分布均匀。在两半部分内分布均匀。设：设： 1 1、 2 2 上半金属板左右部分电荷密度。上半金属板左右部分电荷密度。E1、D1 左半部分介质中场强和电位移。左半部分介质中场强和电位移。E2、D2 右半部分真空中场强和电位移。右半部分真空中场强和电位移。+E1D1E2D2+ 1 1 2+ 2如图作高斯面，由高斯定理如图作高斯面，由高斯定理SSDSdD1111D01011DE同理，右半部分同理，右半部分22D02022DE静电平衡时两导体是等位体，左右两部分极板间电位静电平衡时两导体是等位体，左右两部分极板间电位差相等，即差相等，即2211dEdE2

33、1EE +E1D1E2D2+ 1 1 2+ 2020112由于板上总电量不变，故由于板上总电量不变，故SSS02122左半部左半部分电量分电量右半部右半部分电量分电量总电量总电量联立求解上两式得：联立求解上两式得：00112 00212 极板间场强为：极板间场强为：0022112EEE未充介质未充介质时的场强时的场强极板间电压为：极板间电压为：+E1D1E2D2+ 1 1 2+ 2001212UdEEdU介质表面极化电荷面密度为：介质表面极化电荷面密度为：0101111) 1(2 EPnPe电容：电容：0002112CUSUQC八八. .有介质时的电容器的电容有介质时的电容器的电容自由电荷自由电荷有介质时有介质时相对介电常数相对介电常数 又称电容率又称电容