材料力学第六章弯曲变形

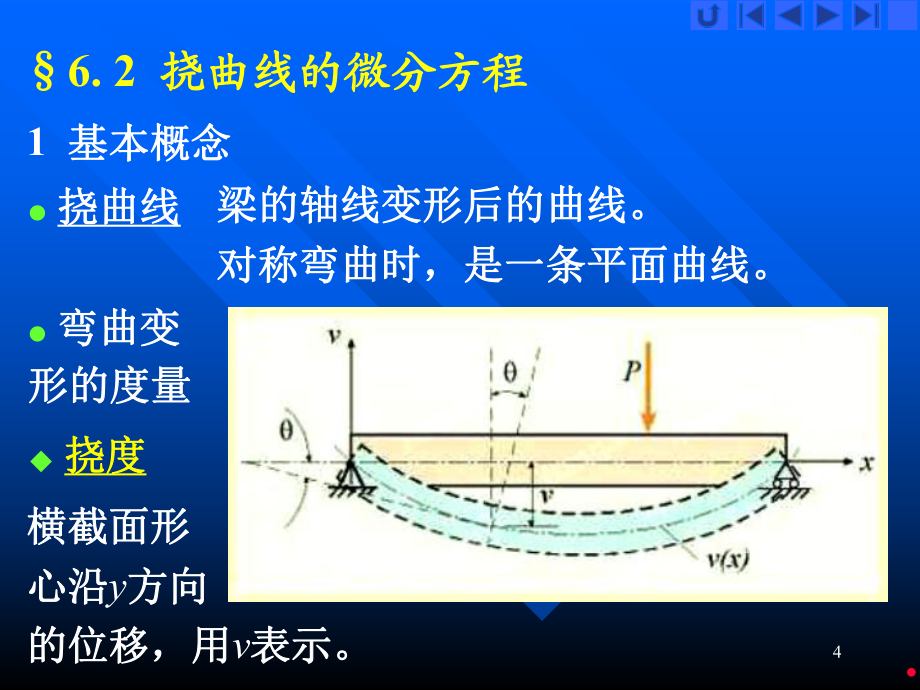
1、1第六章第六章弯弯 曲曲 变变 形形236. 1 工程中的弯曲变形问题工程中的弯曲变形问题l 对梁除了有强度要求外，还有刚度要求。对梁除了有强度要求外，还有刚度要求。u 大多数情况下，要求梁的变形不能过大；大多数情况下，要求梁的变形不能过大；u 一些特殊情况下，要利用弯曲变形。一些特殊情况下，要利用弯曲变形。6. 2 挠曲线的微分方程挠曲线的微分方程l 求解静不定问题需要计算梁的变形。求解静不定问题需要计算梁的变形。l 挠曲线挠曲线梁的轴线变形后的曲线。梁的轴线变形后的曲线。对称弯曲时，是一条平面曲线。对称弯曲时，是一条平面曲线。46. 2 挠曲线的微分方程挠曲线的微分方程1 基本概念基本概念

2、梁的轴线变形后的曲线。梁的轴线变形后的曲线。对称弯曲时，是一条平面曲线。对称弯曲时，是一条平面曲线。l 弯曲变弯曲变形的度量形的度量u 挠度挠度横截面形横截面形心沿心沿y方向方向的位移，用的位移，用v表示。表示。l 挠曲线挠曲线5u 挠度挠度横截面形心沿横截面形心沿y方向方向的位移，用的位移，用v表示。表示。u 转角转角变形后，横截面相对其原来位置转过的角度。变形后，横截面相对其原来位置转过的角度。用用 表示。转角表示。转角 以以逆时针逆时针为为正正。l 挠曲线方程挠曲线方程)(xfv 转角即为挠曲线在该点的切线与转角即为挠曲线在该点的切线与x轴的夹角。轴的夹角。xvddtan62 2 挠曲线

3、的微分方程挠曲线的微分方程上一章中，已得到：忽略剪力对变形的影响时，上一章中，已得到：忽略剪力对变形的影响时，梁对称弯曲时的曲率为梁对称弯曲时的曲率为u 由由高等数学高等数学公式公式EIxMx)()(1)(1x2/ 3222dd1ddxvxv7,)()(1EIxMx)(1x2/ 3222dd1ddxvxv2/ 3222dd1ddxvxvEIxM)(这就是挠曲线的微分方程。这就是挠曲线的微分方程。8l 挠曲线的近似微分方程挠曲线的近似微分方程2/ 3222dd1ddxvxvEIxM)(在小变形的情况下，在小变形的情况下，1ddxv22ddxvEIxM)(u 方程中正负号的确定方程中正负号的确定9

4、l 挠曲线的近似微分方程挠曲线的近似微分方程在小变形的情况下，在小变形的情况下，1ddxv22ddxvEIxM)(u 方程中正负号的确定方程中正负号的确定所以方程中所以方程中应应取取正号正号。EIxM)(22ddxv10l 挠曲线的近似微分方程挠曲线的近似微分方程在小变形的情况下，在小变形的情况下，1ddxv22ddxvEIxM)(u 方程中正负号的确定方程中正负号的确定方程中应取正号。方程中应取正号。EIxMxv)(dd22转角转角:tan注意注意: 挠曲线的近似微分方程仅适用于挠曲线的近似微分方程仅适用于小变形小变形的的平面弯曲平面弯曲问题。问题。xvdd116. 3 用积分法求弯曲变形用

5、积分法求弯曲变形挠曲线近似微分方程挠曲线近似微分方程积分一次，得积分一次，得EIxMxv)(dd22xvdd再积分一次，得再积分一次，得DCxxxEIxMvdd)(其中，其中，C、D为积分常数为积分常数l 边界条件边界条件CxEIxMd)(，由，由边界条件边界条件确定。确定。12l 边界条件边界条件几种典型的边界条件几种典型的边界条件u 简支梁简支梁u 悬臂梁悬臂梁, 0)0(v0)(lv, 0)0(v0)0( vl 连续条件连续条件u 弯曲变形的弯曲变形的对称点对称点处处0v在挠曲线的任意点处，有唯一的挠度和转角。在挠曲线的任意点处，有唯一的挠度和转角。13l 梁的刚度条件梁的刚度条件, m

6、axffmaxl 连续条件连续条件在挠曲线的任意点处，有唯一的挠度和转角。在挠曲线的任意点处，有唯一的挠度和转角。右左DDvv D点和点和C点点的连续条件的连续条件各为什么？各为什么？D点：点：C点：点：右左DD,C右左Cvv右左CCu 中间铰处，挠度连续，转角不连续。中间铰处，挠度连续，转角不连续。014例例 已知已知：简支梁：简支梁受集中力作用。受集中力作用。解解：求求：转角和挠：转角和挠曲线方程。曲线方程。(1) 求支反力，列弯矩方程求支反力，列弯矩方程u 支反力支反力,lPbRAlPaRBu 弯矩方程弯矩方程AC段：段：11xlPbM )0(1ax 15(1) 求支反力，列弯矩方程求支

7、反力，列弯矩方程u 弯矩方程弯矩方程AC段：段：11xlPbM )0(1ax CB段：段：)(222axPxlPbM)(2bxa(2) 列近似微分方程，积分列近似微分方程，积分AC段：段：11xlPbvEI ,211211CxlPbvEI11131161DxCxlPbEIv16(2) 列近似微分方程，积分列近似微分方程，积分AC段：段：11xlPbvEI ,211211CxlPbvEI11131161DxCxlPbEIvCB段：段：)(222axPxlPbvEI 222222)(2121CaxPxlPbvEI22232322)(6161DxCaxPxlPbEIv17(3) 确定积分常数确定积分

8、常数u 连续条件连续条件)()(21avavu 边界条件边界条件)()(21avav,21CC 21DD 01x时时,;01vlx 2时时,02v代入相应的方程，得代入相应的方程，得:021 DD21CC )(622bllPb18u 边界条件边界条件01x时时,;01vlx 2时时,02v代入相应的方程，得代入相应的方程，得:021 DD21CC )(622bllPb将求得的积分常数代回方程，得将求得的积分常数代回方程，得:AC段：段：, )3(621221xbllPbvEI)(6212211xbllPbxEIvCB段：段：)(3)3(62222222axblxbllPbvEI19将求得的积分

9、常数代回方程，得将求得的积分常数代回方程，得:AC段：段：, )3(621221xbllPbvEI)(6212211xbllPbxEIvCB段：段：)(3)3(62222222axblxbllPbvEI)()3(632222222axblxxbllPbEIv(4) 求最大转角和最大挠度求最大转角和最大挠度20(4) 求最大转角和最大挠度求最大转角和最大挠度u 最大转角最大转角由图，最大转角由图，最大转角可能发生在可能发生在A点点或或B点。点。EIlblPbA6)(22EIlblPab6)( EIlalPabB6)( u 最大挠度最大挠度21u 最大挠度最大挠度经分析，最大挠经分析，最大挠度发生

10、在度发生在AC段。段。01 v令：令：3220blx322max)(39blEIlPbf经讨论知，不论经讨论知，不论P力作用在何处，最大挠度总发力作用在何处，最大挠度总发生在中点附近生在中点附近(或中点或中点)。所以可。所以可近似地近似地以中点的以中点的挠度作为最大挠度。挠度作为最大挠度。226. 4 用叠加法求弯曲变形用叠加法求弯曲变形l 叠加法叠加法EIxMxv)(dd22在在线弹性线弹性小变形小变形的条件下，得到挠曲线近似的条件下，得到挠曲线近似这是一个这是一个线性线性的常微分方程。的常微分方程。微分方程微分方程在第四章中，证明了在在第四章中，证明了在小变形小变形的条件下，弯矩与的条件下

11、，弯矩与外载荷成线性关系，可用叠加法求弯矩图。外载荷成线性关系，可用叠加法求弯矩图。设：设：)()()(21xMxMxM23EIxMxv)(dd22这是一个这是一个线性线性的常微分方程。的常微分方程。挠曲线近似微分方程挠曲线近似微分方程设：设：)()()(21xMxMxM,)(dd1212EIxMxvEIxMxv)(dd2222则共同作用时：则共同作用时：)(dd22xMxvEI)()(21xMxM212ddxvEI222ddxvEI2212d)(dxvvEI24则共同作用时：则共同作用时：)(dd22xMxvEI)()(21xMxM212ddxvEI222ddxvEI2212d)(dxvvE

12、I即：共同作用下的挠度等于分别在即：共同作用下的挠度等于分别在M1(x) 、M2(x)单独作用下的挠度的代数和。单独作用下的挠度的代数和。综合以上讨论得到：综合以上讨论得到：在在线弹性线弹性小变形小变形的条件下，的条件下，外载荷外载荷与与挠度挠度 (力与力与位移位移)成线性关系，可用成线性关系，可用叠加法叠加法计算梁的挠度。计算梁的挠度。21vvv25l 叠加法的基础叠加法的基础特别是：特别是：1、2、3 、 4、5、 6 。熟悉简单载荷作用下的挠度和转角。熟悉简单载荷作用下的挠度和转角。见教材见教材 p. 188 表表6.1 。l 叠加法的两种类型叠加法的两种类型(1) 载荷叠加法载荷叠加法

13、将载荷分解为几个简单载荷，分别求解后，将载荷分解为几个简单载荷，分别求解后，进行叠加；进行叠加；(2) 变形叠加法变形叠加法在内力不变的前提下，将梁分解在内力不变的前提下，将梁分解(或刚化或刚化)为为几段，求出各段的变形，然后进行叠加。几段，求出各段的变形，然后进行叠加。26例例 3 已知已知： q , l , EI = 常数。常数。解解：求求：vC , B。 分解为三个分解为三个简单载荷。简单载荷。27u 由表由表7.1 中的中的5EIqlvC384541EIqlB2431u 由表由表7.1 中的中的628u 由表由表7.1 中的中的5EIqlvC384541EIqlB2431u 由表由表7

14、.1 中的中的4EIPlvC4832EIPlB1622EIql484EIql16329u 由表由表6.1 中的中的8EIPlvC4832EIPlB1622u 由表由表7.1 中的中的6EImlvC1623EImlB33EIql164EIql33EIql484EIql16330u 由表由表7.1 中的中的6EImlvC1623EImlB33EIql164EIql33u 叠加叠加321CCCCvvvv321BBBBEIql384114EIql4811331例例 4 已知已知： q , l , EI = 常数。常数。解解：求求：vC , C。 表中没有对应表中没有对应的情况。的情况。方法：方法：凑成

15、凑成表中相表中相应的情况。应的情况。再分为两种载荷。再分为两种载荷。u 由表由表7.1 中的中的332再分为两种载荷。再分为两种载荷。u 由表由表7.1 中的中的3EIqlvC841EIqlC631u 由表由表7.1 中的中的3EIlqvB8)2/(42EIlqB6)2/(32,1284EIqlEIql48333u 由表由表7.1 中的中的3EIlqvB8)2/(42EIlqB6)2/(32,1284EIqlEIql483u 注意，变形后注意，变形后BC为直线。为直线。22212CCCvvvEIql12842Bv2/2lB2483lEIqlEIql3847422BCEIql4833422212

16、CCCvvvEIql12842Bv2/2lB2483lEIqlEIql3847422BCEIql483所以所以21CCCEIql487321CCCvvvEIql38441435例例 5 已知已知：P, l, EI, EA。解解：求求：vE 。 (1) 将刚架看成将刚架看成是刚体是刚体则则AB相当于简相当于简(2) 刚架变形刚架变形支梁。支梁。1Ev2Ev2/Bvl 思路思路36(1) 将刚架看成将刚架看成是刚体是刚体则则AB相当于简相当于简(2) 刚架变形刚架变形支梁。支梁。1Ev2Ev2/Bvl 求求 vB(3) CD看成看成刚体刚体1Bv(4) BC看成看成刚体刚体37l 求求 vB(3)

17、 CD看看成成刚体刚体1Bv(4) BC看看成成刚体刚体,2Bv3Bvl 具体计算具体计算u 对对BC，由表，由表7.1中的中的1EIlPvB32/31u CD的压缩变形的压缩变形EAlPvB2/238l 具体计算具体计算u 对对BC，由表，由表7.1中的中的1EIlPvB32/31u CD的压缩变形的压缩变形EAlPvB2/2u CD的弯曲变形，由表的弯曲变形，由表7.1中的中的2EIlPC22/ 所以，所以，CBlv3EIlP32/ 321BBBBvvvvEIPl323EAPl239u CD的弯曲变形，由表的弯曲变形，由表7.1中的中的2EIlPC22/ 所以，所以，CBlv3EIlP32

18、/ 321BBBBvvvvEIPl323EAPl2u 对简支梁对简支梁AB, EIPlvE4831又又:BEvv212由表由表7.1中的中的440EIPlvB323EAPl2u 对简支梁对简支梁AB, EIPlvE4831又又:BEvv212由表由表7.1中的中的421EEEvvvEIPl483EIPl33EAPl4416. 5 简单静不定梁简单静不定梁 本节讨论简单静不定梁的求解。本节讨论简单静不定梁的求解。l 例子例子车床上被加工的车床上被加工的工件。工件。u计算简图如图计算简图如图是一次静不定是一次静不定问题。问题。l 基本概念基本概念u 静定基静定基42l 基本概念基本概念u 静定基静

19、定基将静不定系统中的将静不定系统中的多余约束多余约束解除解除后，得到的后，得到的“静定基本系统静定基本系统”。u 相当系统相当系统在静定基上加上外载荷以及多余约在静定基上加上外载荷以及多余约束力，便得到束力，便得到受力受力和和变形变形与静不定与静不定系统完全相同的系统完全相同的“相当系统相当系统”。l 本例中本例中u 解除解除B处可处可动支座约束，动支座约束，得到得到静定基静定基。43u 解除解除B处可动处可动支座约束，得支座约束，得到到静定基静定基。u 在静定基上在静定基上加上加上P和和RB, 得得到到相当系统相当系统。PRBu 求求B点挠度点挠度用叠加法用叠加法44u 在静定基上在静定基上加上加上P和和RB, 得得到到相当系统相当系统。PRBu 变形协调条件变形协调条件u 求求B点挠度点挠度BRBPBBfff)()(0用叠加法用叠加法BRBPBBfff)()(u 具体计算具体计算B点挠度点挠度45u 变形协调条件变形协调条件0BRBPBBfff)()(u 具体计算具体计算B点挠度点挠