空间立体几何点线面判断与证明

1、常州知典教育一对一教案学生：年级：学科：数学 授课时间： 月 日授课老师：赵鹏飞空间立体几何点线面判断与证掌握空间立体几何中的点线面之间的关系，平行，相交，垂直，异面，重合等等，（教学目面面 平行等方法和步骤了解关于几何体中一些基本的计算和比值及证明面面垂直到程度15%比导致证明失分使用性质时没有给出应有的条证明时对判断的方法出现错误思维学生薄弱点导致扣分，计算的失误使得自己失分内上次作业完成情况优良中差课前检考向1空间中点、线、面位置关系的判断1 .平面的基本性质的应用教公理1：证明“点在面内”或“线在面内”.学（2）公理2及三个推论：证明两个平面重合，用来确定一个平面或证明“点线 共.面”

2、过（3）公理3：确定两个面的交线，尤其是画截面图或补体时用到，证明“三点共程线”“三线共点”.讲 义要证明“点共线”可将线看作两个平面的交线，只要证明这些点都是这两个平部分面的公共点，根据公理3可知这些点在交线上，因此共线.空间中点、线、面之间的位置关系.2.直线与直线直线与平面平面与平面直线与直线直线与平面平面与平面相交关系独有关系(1)已知m, n表示两条不同直线，a表示平面，下列说法正确的是若 ma，na，贝。mn若 ma， n? a，贝。mn若 ma， mn，贝。na若 ma，mn，贝。na(2)下列命题正确的是()若两条直线和同一个平面所成的角相等，则这两条直线平行若一个平面内有三个

3、点到另一个平面的距离相等，则这两个平面平行若一条直线平行于两个相交平面，则这条直线与这两个平面的交线平行若两个平面都垂直于第三个平面，则这两个平面平行【解析】(1)对于选项A , m与n还可以相交或异面；a； ?对于选项C，还可 以是na或 n与a相交.n，还可以是na或？对于选项D(2)对于命题A，这两 条直线可以相交或为异面直线，.A错误；对于命题B，这两个平面可以相交，.B错误；对于命题D，这两个平面还可能相交，.D错误；而由线面平行的性质定理可证C正确.故选C.【答案】(1)B (2)C【点拨】解题(1)根据空间线面、面面、线线平行的判定与性质、垂直的判定时 要注意充分利(2)解题注意

4、空间位置关系的各种可能情况.与性质逐个进行判断， 用正方体(或长方体)模型辅助空间想象.而四易3解决空间位置关系问题的方法解决空间中点、线、面位置关系的问题，首先要明确空间位置关系的定义然 后通过转化的方法，把空间中位置关系的问题转化为平面问题解决解决位置关系问题时，要注意几何模型的选取，如利用页长)方体模型来解决 问题.考向2异面直线所成的角1 .两条异面直线所成的角过空间任意一点分别引两条异面直线的平行直线，那么这两条相交直线所成的n? ,则。锐角或直角叫作这两条异面直线所成的角.若记这个角为。，02?2.判定空间两条直线是异面直线的方法判定定理：平面外一点A与平面内一点B的连线和平面内不

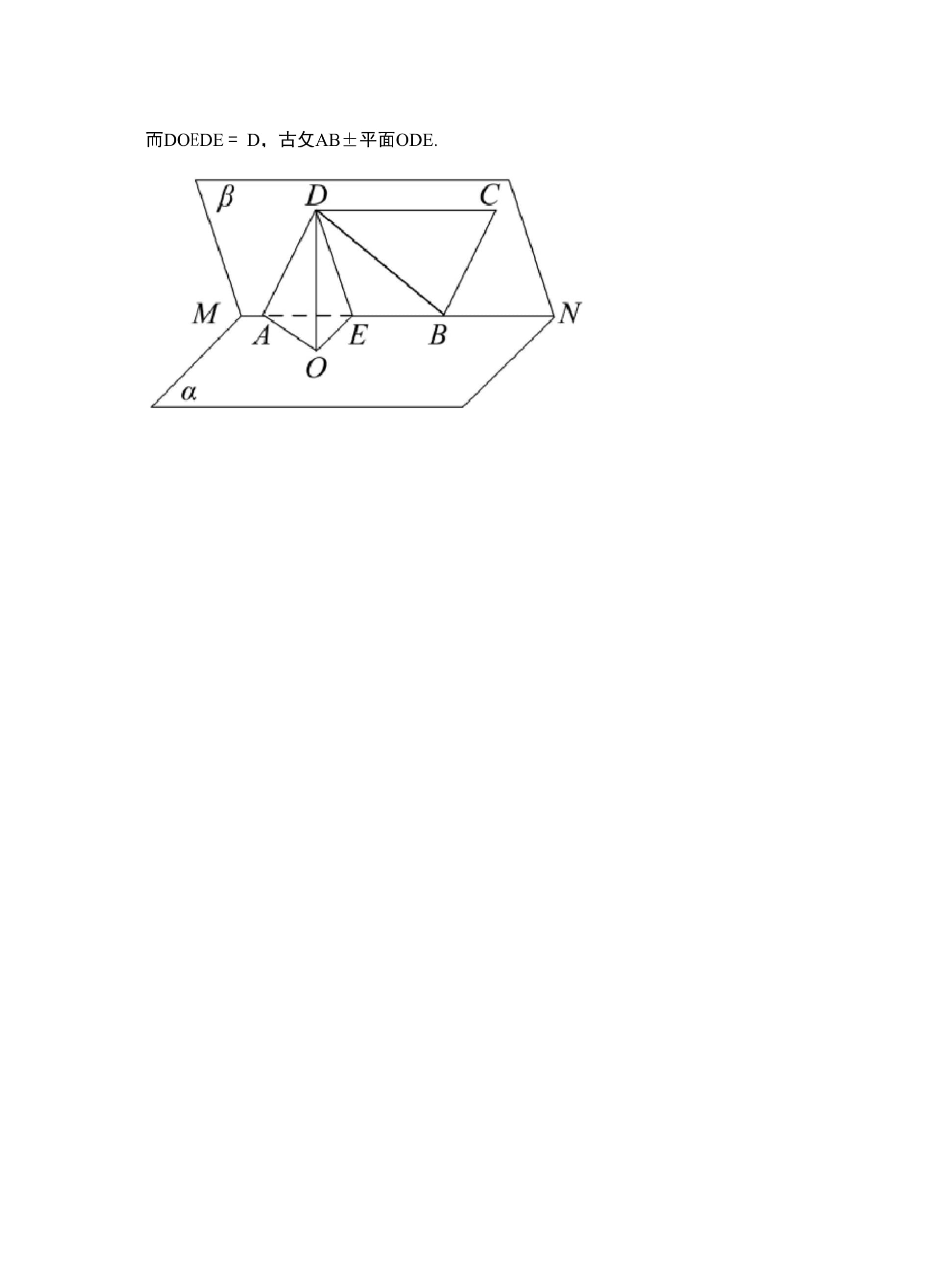
5、经过点B的直线是异面直线.反证法：证明两直线平行、相交不可能或证明两直线共面不可能，从而可得 两直线异面.(2014 大纲全国，4)已知正四面体ABCD中，E是AB的中点，则异面直线CE与BD所成角的余弦值为()13A. B. 6613C. D. 33 两 B，A 内，B 在面 ABCD。，菱形 60 的大小为 B-MN- a如图，已知二面角(2).点在棱MN上，/BAD = 60，E是AB的中点，DOL面a，垂足为O.证明人上平OD求异面直BO所成角的余弦值解(1如图，A的中，连CE,EB.NCEF即为异面直线CE与BD所成的角.-CE3由余1设正四面体的棱长为2 ,则CE = CF = 3

6、 , EF = BD= 1. 2-CE3由余弦定理得cosZCEF = . 62CE-EF3.CE与BD所成角的余弦值为.故选B.6aa ,.DO?AB.DO(2)证明：如图广.，AB连接BD，由题设知，ABD是正三角形.又E是AB的中点，.DEAB.而DOE而DOEDE = D，古攵AB平面ODE.因为BCAD所以BC与OD所成的角等于AD与OD所成的角，即匕ADO所 成的角. OD与BC是异面直线由知AB1平面ODE所以ABXOE.又 DEXAB于是ZDEO是二面角a-MN-B的平面角，从而ZDEO = 60.不妨设AB = 2，贝U AD = 2.易知DE = 3.RDO中DDsin 6

7、D连A , RAO中coADA古攵异面直BO所成角的余弦值点解(1 的关键是选取合适的点作出异面直线的平行线解(2时注意异面直线所成的角归 结到-个三角形里.特别为直角三角形SS3ESO求异面直线所成角的方法作：利用定义转化为平面角，对于异面直线所成的角，可固定一条、平移一 条，或两条同时平移到某个特殊的位置，顶点选在特殊的位置上.证：证明作出的角为所求角.求：把这个平面角置于一个三角形中，通过解三角形求空间角.e 注意两异面直线所成的角归结到一个三角形的内角时，容易忽视这个三角形的内角可 能等于两异面直线所成的角，也可能等于其补角.考向3线面平行的判定与性质直线与平面平行的判定定理与性质定理

8、 文字语言图形语言符号语言判不在平面内的一条直线与a?l?此平面内的一条直线平行，定？ al?a?a简定 则该直线与此平面平行(？ al )线面平行? 记为线线平行理.一条直线与一个平面平行，性则过这条直线的任一平面aa?质？ b?aBa与此平面的交线与该直线？平简记为线面平线平行直线与平面平行的判定定理和性质定理中的三个条件缺一不可；线面平行的性质 定理可以作为线线平行的判定方法.(2014 -北京，17 , 14分)如图，在三棱柱ABC-ABC中，侧棱垂直E, F分111 于底面，ABBC, AA=AC = 2, BCE, F分别是AC, BC的中点.111(1)求证：平面ABE平面BBC

9、C； 11(2)求证：CF 平面ABE； 1(3)求三棱锥E-ABC的体【思路导引】(1)利用已知条件转化为证明AB平面BBCC； (2)取AB的中11 点G,构造四边形FGEC,证明其为平行四边形，从而得证；(3)根据题中数据代 入1公式计算即可.【解析】(1)证明：在三棱柱ABC-ABC中BB底面ABC.山所以BBAB. 1 ,BCXAB又因为所以AB平面BBCC. 11所以平面ABE平面BBCC. 2)证明：如图，取AB中点中点6,连接EG , FG.因分别AB的中点所FA , FA因A, A的中点所FE , FE所以四边FGE为平行四边形所E又因E平AB平AB所11平AB(3因AABA

10、B3AB所A所以三棱AB的体1113V=S-AA= XX3X1X2 = .1ABC3233 1.证明线面平行问题的思路(一)作(找)出所证线面平行中的平面内的一条直线；证明线线平行；根据线面平行的判定定理证明线面平行.证明线面平行问题的思路(二)在多面体中作出要证线面平行中的线所在的平面；利用线面平行的判定定理证明所作平面内的两条相交直线分别与所证平面平 行；证明所作平面与所证平面平行；转化为线面平行.(2013 -江苏，18 , 13分)如图，在边长为1的等边三角形ABC中，ABF将.G交于点DE与AF的中点，BC是F, AE=AD上的点，AC, AB分别是E, D.2沿AF折起，得到如图所

11、示的三棱锥A-BCF,其中BC = .2(1)证明：。平面BCF；(2证明平AB(3A时，求三棱DE的体积3解(1证明：在等边三角AB中AAAA，在折叠后的三棱BC中也成立EDB.LDEIIBC. .DE?平面BCF , BC?平面BCF ,.DEII 平面 BCF.证明：由图，在等边三角形ABC中，F是BC的中点，AFBC，在三棱锥中仍有AFXCF ,1BF = CF = . 22L在三棱锥 A-BCF 中，BC =, 2222 , CF = BF+ aBCaCFBF.又 VBFAAF = F ,ACF平面 ABF.由(1)可知GECF，结合(2)可得GEL平面DFG.V = V = VDF

12、GEDEGF11= X EG-FG-DG-23 .1111?31?XXX = XX323332?3 = .32考面面平行的判定与性平面与平面平行的判定定理与性质定 文字语图形语符号语一个平面内的两条相交判ab?则这定 线与另一个平面平行，? Ba?一个平面内的两条相交判ab?则这定 线与另一个平面平行，? Ba?Panb =简记为线面两个平面性如果两个平行平面同时和aB ?质？?ab ayan=那么它们第三? ?平行(定 B a)?理 平行面面平行B b个平面相交，定？b=ynB的交线平行 理的底面是正方形，的底面是正方形，DC如图，四棱柱ABCDX底面0=中心，AAB, AA=u 平面BDA

13、证明：平面(1)BCD；(2)求三棱柱ABD-ABD的体积.山注意平面与平面平行的性质定理实际上给出了判定两条直线平行的一种方法， 一定是第三个平面与两平行平面相交，其交线平行.是底面BA-ABCDOABCD 211112.解(1证明：由题设知BD.四边B是平行四边形BB平CB 11平C.AD BC BC, mF.四边形ABCD是平行四边形，h-ABIIDC.又AB?平面CDB , 111 ABII 平面 CDB. e 又VBDAAB = B ,平面 ABDII 平面 CDB. 111(2)VAO 平 面 ABCD ,.AO 是三棱柱 ABD-ABD 的高.又 VAO = AC = 1 , A

14、A = 2 ,222 -AO = AA1. =.AO111 又VS= X2X2= 1 , ABD2fi.VABD-ABD = S-AO = 1. 111ABD1【点拨】解题(1)需将面面平行关系转化为线面平行，再转化为线线平行， 通利用线面垂直的判的关键是选易求高的底面，(2)解题过取特殊四边形来完成 证明；定找高.SS3ESO判定面面平行的四个方法利用定义：即判断两个平面没有公共点.(2利用面面平行的判定定理利用垂直于同一条直线的两平面平行.利用平面平行的传递性，即两个平面同时平行于第三个平面，则这两个平面 平行.平行问题的转化关系线线平行面面平仃的性质（2014 -十校联考，18 , 12

15、分）如图，在三棱柱ABC-ABC中，D是111BC上一点，且人日平面ACD, D是BC的中点，求证:平面ABD 平面ACD.11111111证明：如图，连接AC交AC于点E ,连接ED. J.，四边形AACC是平行四边形， h-E 是 AC 的中点.AB II 平面 ACD，平面 ABCA平面 ACD = ED , 1111A .ED II的中点，B的中点的中点，B.四边BD为平行四边形.BD II CD. 11又ABABD =B , DEADC = D , .平面 ABD II平面 ACD. 111考向5线面垂直的判定与性质直线与平面垂直的判定定理及性质定理文字语言图形语言符号语言?判a,b

16、?a 一条直线与平面内的两定Ob=Ea ?la则该条相交直线都垂直，al定 直线与此平面垂直bl理垂直于同一个平面的两质aa ?ab ?ba ?定条直线平行 理上底面PO为中心的菱形，O中，底面是以ABCD-P如图，四 n 1ABCD，AB = 2，ZBAD=，M 为 BC 上一点，且 BM=.(1证明日上平PO(2MA，求四棱ABM的体积思路导(1由余弦定理、勾股定理等知识先OB，再由线面垂直的判定定理证明； 将底面四边形ABMO分为ABO与MBO来求面积，根据(1)中结果，利用 勾股定理、余弦定理求出PO,代入棱锥的体积公式求解.【解析】(1)证明：如图，连接OB,因为四边形ABCD为菱形

17、，O为菱形中心，所以AOXOB.n因为/BAD=, 3n故 OB = ABsin/OAB = 2sin = 1. 6n1 又因为 BM=,且 /OBM =, 32222 - 2OB-BM-OB + BMcosZOBMA在 OBM 中，OM = 2n113?2? .cos = X - 2X1 = 1 + X2432?222，故 OMBMBM.所以 OB =OM +又PO底面 ABCD，所以 POBC.又 OM?平面 POM , PO?平面 POM , OMCIPO=O ,所以BC平面POM.n(2)由(1)可得，OA = AB-cosZOAB = 2-cos 3. = 6 .设PO = a,由P

18、O底面ABCD知，POA为直角三角形，2222 + 3.OA P故A=POa+由POM也是直角三角形，OPPcoAB中ABAABAB如图连A2co由已MA , AP为直角三角形2PA ,=舍，p此omaoabm四边AOBO所以四棱ABM的体P.ABMABM1四边而四&爵* 1.证明直线与平面垂直的一般步骤找与崔：在已知平面内找或作两条相交直线与已知直线垂直.证：证明所找到的或所作的直线与已知直线垂直.用：利用线面垂直的判定定理，得出结论.2.判定线面垂直的四种方法利用线面垂直的判定定理.利用“两平行线中的一条与已知平面垂直，则另一条也与这个平面垂直”.利用“一条直线垂直于两平行平面中的一个，则

19、与另一个平面也垂直”(3).利用面面垂直的性质定理.考面面垂直的判定与性平面与平面垂直的判定定理及性质定 文字语图形语符号语一个平面过另一个平面的一条垂线，?la?定 面互相垂直理性定l? 一个平面过另一个平面的一条垂线，?la?定 面互相垂直理性?相垂直，?质P?la 相垂直，?质P?la ?l个平面内垂直于交线的aEB?=a定直线垂直于另一个平面al理ABC如图，在三棱锥，江苏，(2014-1614分)P-AACA的中点.已知，分别为棱，EFPCACABPX, P，中，D5.AACA，=BC8DF=，=6 A 直线求证：(1)P平面 DEF；.BDE平面ABC平面(2)再运用直线与平面思路

20、导引【】(1)利用三角形中位线的 性质找到线线平行，要证线面垂直可平行的判定定理进行求证；(2)要证面面垂直可考虑寻找线面垂直，考虑寻找线线垂直，利用勾股定理可证线线垂直.的中点，AC, PCE ,D(1)】【证明因为分别为棱APDE所以.，DEF平面?DE , DEF平面?AP又因 为 所以直线PA平面DEF.因为D , E , F分别为棱PC , AC , AB的中点，PA=6 , BC = 8，所以DEPA, 11DE = PA=3 , EF = BC = 4. , DED 又因 D 所 DE9, DEAD ,所DA因AEA平ABE平AB所D平ABD平BD 所以平BD平AB.面面垂直证明

21、的两种思路用面面垂直的判定定理，即先证明其中一个平面经过另一个平面的一条垂线;用面面垂直的定义，即证明两个平面所成的二面角是直二面角，把证明面面 垂直的问题转化为证明平面角为直角的问题.垂直问题的转化关系判定判定判定 *线罕直云线面垂直2面面垂直性质考向7线面角、二面角的求法1 .线面角当la时，线面角为90 .当la或l?a时，线面角为0 . (3)线面角。的范围：0WOW90 .2.二面角(1)如图，二面角 a-l-B,若01,OA?a, OB? 3, OAl, OBl,则 的平面角.B -l- a就叫作二面角AOBZ.囤3 四边形,BA=BD 囤3 四边形,BA=BD = 2,AD =

22、2, PA=PD = 5, E, F 分别是棱 AD, PC 的中点.证明：平面PAB.若二面角 P-AD-B 为 60,证明：平面PBC平面ABCD；求直线EF与平面PBC所成角的正弦值.【思路导引】(1)因为E, F分别是所在棱的中点，可取PB的中点M,证明四 边形AMFE是平行四边形，然后利用线面平行的判定定理证明.(2)连接PE, BE,由题意知ZPEB = 60，在 PEB中利用余弦定理证出BE PB.又BEAD,然后利用线面垂直和面面垂直的判定定理证明；由知BE 上平面PBC,则/EFB即为直线EF与平面PBC所成的角.【解析】(1)证明：如图，取PB中点M，连接MF ,AM.因为

23、F为PC中点.1 古攵 MFBC 且 MF = BC. 2 由已知有 BCAD , BC = AD.又由于E为AD的中点，因而 MF AE 且 MF = AE ,故四边形AMFE为平行四边形，所以EF AM.又AM?平面PAB，而EF?平面PAB , 所以EF 平面PAB.BE , PE证明：如图，连接2).因为PA=PD , BA = BD，而E为AD的中点，故 PEAD , BEAD ,所以ZPEB为二面角P-AD-B的平面角.A中，PA,可解P2AB中，BBA，可解B1PE 中 PB , PE6由余弦定理，可解P从 PB9, BPBABA从BB ,因B平PBB平ABC，所以平PB平ABC

24、如图，连B知B1平PB所EF为直E与平PB所成的角P及已知，AB为直角11MP，可A , EB1B，故REB中siEF1E1所以直E与平PB所成角的正弦值.111.求空间角的三个步骤找：即找出相关的角；证：即证明找出的角即为所求的角；计算：即通过解三角形的方法求出所求角.2.空间角的找法线面角找出斜线在平面上的射影，关键是作出垂线，确定垂足.二面角二面角的大小用它的平面角来度量，平面角的常见作法有：定义法；垂面 法.其中定义法是最常用的方法.巩固练习1如图，在四棱ABC中底ABC是矩形上平ABCAABP于.(1求证AP(2求直C与平AC所成的角的余弦值2.如图所示，在四棱锥S-ABCD中，底面

25、ABCD是菱形，SA平面ABCD，M， 课N分别为SA，CD的中点.堂(1)证明：直线MN平面 SBC；练习 证 明：平面SBD1平面SAC.如图，在直角梯形 ABCD 中，ADBC,/ADC = 90, AB=BC.把 BAC 沿AC折起到APAC的位置，使得P点在平面ADC上的正投影O恰好落在线段 A上，如图所示，分别为PC的中点(1求证：平0平AP(2求证平P0(3ACA，求四棱CF的体解：(1)证明：V PA平面 ABCD , AB?平面 ABCD , aPAAB. vABAD , ADAPA=A ,AD?平面 PAD ,PA?平面 PAD , aAB 平面 PAD. vPD?平面 PAD , AABPD. VBMPD , ABABM = B , AB?平面 ABM , BM?平面 ABM ,APD 平面 ABM. .AM?平面 ABM ,aAMPD. (2)由(1)知，AMPD，又 PA=AD , 则M是PD的中点.在 RtPAD 中，AM = 2 ,错 22 ,DC3CDM 中，MC = MD =+在 Rt题