2023年高考数学一轮复习（学生版）：第十一单元空间向量及其应用

§11.1空间向量及其运算

(对应答案分册第35~36页)

................................圜基础知识……，夯实基础巩固提升

«《知识清单》>

1.空间向量的有关定理

共线

向量对空间任意两个向量a,次6,0),a”6的充要条件是存在唯一的实数4使得

定理

共面

2如果两个向量a,6不共线，那么向量"与向量共面的充要条件是存在唯一的有序

二亚实数对(xj),使得夕=%

/E埋

空间

向量如果三个向量a,6,c不共面，那么对空间任一向量夕，存在有序实数组｛x,卜力，使得

基本p=xa.其中｛a,6,4叫作空间的一个基底.

定理

2.两个向量的数量积(与平面向量基本相同)

(1)两向量的夹角:已知两个非零向量3,6,在空间中任取一点。，作

而二&则叫作向量a与6的夹角，记作<a,6>.通常规

定，<<a,b><.若<46>苦则称向量a6互相垂直,记作(3_1/?;若<3,6>=0或

va,6>n,则称向量a,6互相平行，记作allb.

(2)两向量的数量积

两个非零向量a,6的数量积a6=.

(3)向量的数量积的性质

@)ae=/3/2osva,e>(其中e为单位向量)；

②a_L/x=>;

③/

④1abi同间.

(4)向量的数量积满足如下运算律

(iXAa)-b=A(a-b)-,

②a6=b式交换律)；

③a(b+4=:(分配律).

3.空间向量的坐标运算

(1)设团，曲由),6=(仇生甸，则

a+b=®+优，力+6,为+bi),

a-6=(&-仇，力-笈,力-仇)，

Aa=(Aai,Aa2,Aai),

a-b=i：b,

ax.60al优+a2b2+否0=0,

allb^ai=Ab].,a2=Ab2,a3=Ab3(A^^,

cos<a,b>=-^~

|a||b|

_。速1+。2b2+a3b3

Ja」+a介面Jb：+b，+b专

(2)设A(xi,yi,zi),B(X2,yz,Z2),

则万=砺C?="…乙-Ni；

特别提醒

(1)注意向量夹角与两直线夹角

的区别.

(2)共线向量定理中all6=存在唯一

的实数R,使3=助,易忽视6。0

的情况.

(3)共面向量定理中，注意有序实数对

(加0是唯一存在的.

(4)向量的数量积满足交换律、分配

律，但不满足结合律，即

(?6)•。不一定成立.

««分—基■»》

【概念辨析】

判断下面结论是否正确.(对的打"V",错的打"x")

(1)空间中任意两非零向量3,6共面.

(2)在向量的数量积运算中(a6)〈=a(b)

(3)对于非零向量6,由ab=bc得a=c.

(4)若｛a,6©是空间的一个基底，则a,中至多有一个零向量.

【对接教材】

如图，在四面体0/6。中,O4_L8cO8_L/C试判断。6■与的关系.

下列命题：

②若是空间中任意四点，则有荏+前+而而7割

②同-向=忖+川是a,6共线的充要条件；

渊共线，则a与6所在的直线平行；

④对空间任意一点。与不共线的三点48,£若方=＜¥0/1+yOB+的4其中

x/,ZGR）,则R48c四点共面.

其中假命题的个数是（）.

A.lB.2C.3D.4

【易错自纠】

已知空间四边形O48C其对角线为O8/CM/V分别是边04,C8的中点，点G

在线段M/V上，且/V/G=2G/V,则用向量?赤，沆表示向量而正确的是（）.

K0G=0A-h^0B-f-0C

B^0G=^0A-^；0B-^；0C

C^OG=^OA+^OB+^OC

633

D^OG=^0A-^OB-^OC

633

下列四个结论正确的是（）.

A.对于任意向量a,6,若a6=0,则＜a,6＞苦

B.若空间中点。,48,。满足沆三函彳砺则48c三点共线

C.空间中任意向量3,6（都满足（36）七二3（6。

D.已知向量a=（l,LM，6=（2x4）,若x＜|,则＜a,6＞为钝角

讲考点考向•，精研考向锤炼技能

d点鎏空间向量的线性运算【题组过关】

1.

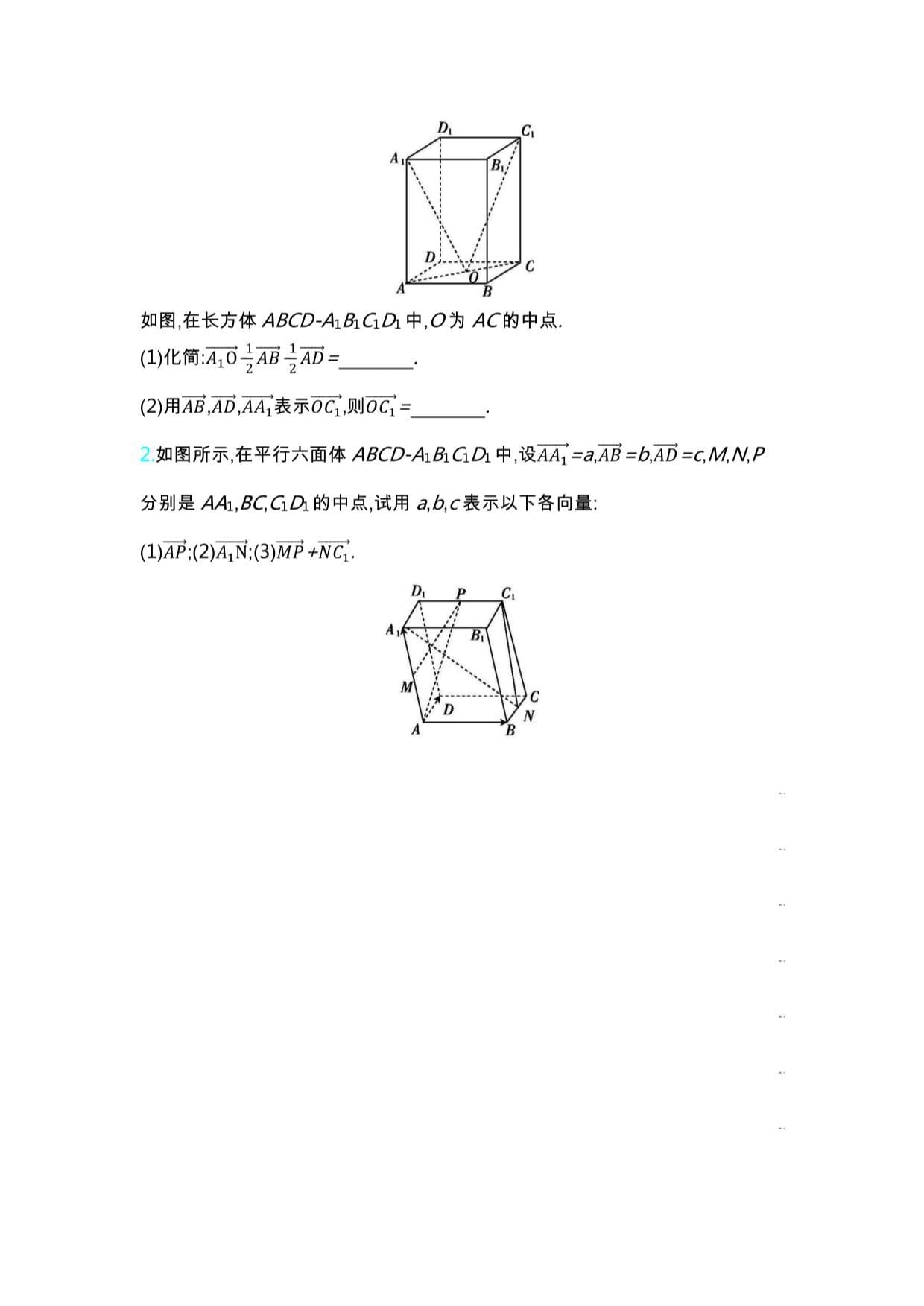
如图，在长方体/8U。-481Gs中，。为力。的中点.

⑴化简:砧弓而曰诟二-

(2)用石，前，丽*表示^则西＞=.

如图所示,在平行六面体ABCD-AiBiCiDi中，设彳否=a,都=b,而=c,M/V,P

分别是/4,8CGS的中点，试用a,6,c表示以下各向量:

(1)AP;(2)^N;(3)MP+NC1.

一用已知向量表示未知向量的解题策略

(1)用已知向量来表示未知向量，一定要结合图形，以图形为指导是解题的关

(2)要正确理解向量加法、减法与数乘运算的几何意义.首尾相接的若干向量

之和，等于由起始向量的始点指向末尾向量的终点的向量，我们可把这个法则称为

向量加法的多边形法则.

(3)在立体几何中要灵活应用三角形法则,向量加法的平行四边形法则在空间

中仍然成立.

至良❷共线、共面向量定理的应用【题组过关】

已知分别是空间四边形的边的中点，用向量方

法求证：

四点共面；

(2)8011平面EFGH.

如图所示,已知斜三棱柱/8U-481G,点M/V分别在上,且满足

宿=麻7，丽=碗（04心1）.判断向量标是否与向量存,旃＞共面.

G

在求一个向量由其他向量来表示时，通常是利用向量的三角形法则、

平行四边形法则和共线向量的特点，把要求的向量逐步分解，向已知向量靠近.常

见的向量处理方法见下表：

三点（月4㈤共线空间四点（M44向共面

巨^=力而且同过点户MP=AMA+>MB

对空间任意一点

对空间任意一点O,0P=0M+AMA+/而

--------->,>'''>

OQP=OA+植B

对空间任意一点

<9,OP=AOA+(1-对空间任意一点O,0P=AOM+顺+(l-x^OB

A)OB

CH®空间数量积及应用【典例迁移】

阳健］如图所示，已知三棱锥48。的每条棱长都为LSRG分别是

力民力。,。的中点，计算:

⑴乔研(2)苗丽

C

【变式设问】在本例条件下，求证:£G，/8.

(1)空间向量数量积的计算方法

册义法:设向量46的夹角为，则a-b=/3//b/cos6.

②^标法:设权(牙1分,21),6=(检以为,则a-b=x\X2+yiyi+z\Z2.

(2)数量积的应用

②求夹角:设向量a,b所成的角为，则cos8=品，进而可求出两异面直线

所成的角.

②求长度(距离):运用公式舒=?可可使线段长度的计算问题转化为向量数

量积的计算问题.

③解决垂直问题:利用以防？6印(衣0,6工0),可将垂直问题转化为向量数

量积的计算问题.

【追踪训练】如图,建立空间直角坐标系。-噂正方体的

棱长为1,顶点/位于坐标原点，其中点8(1,0,0),点。(0,1,0),点/(0,0,1).

(1)若£是棱8匕的中点，尸是棱的中点,G是侧面的中心，分别求

出向量岳，冠，刀的坐标;

(2)在⑴的条件下，分别求出(而+而)•而，府州值.

.....£3方法技巧＞方法探究分类突破

0延突破©利用空间向量求距离和异面直线的夹角

阳硼如图所示，已知空间四边形力8。的每条边和对角线长都等于1,E,F,G

分别是力民力。,。的中点，计算：

Q)&7的长；

(2)异面直线ZG与上所成角的余弦值.

C

E方法总结

(i)利用空间向量数量积求夹角:

设向量所成的角为日则cos

8=能，进而可求两异面直线所成的

|可出|

角.

(2)利用空间向量数量积求长度(距

离):运用公式舒可使线段长度

的计算问题转化为向量数量积的计

算问题.

【突破训练】如图，已知平行六面体ABCD-A1BCD1中，底面28。是边

长为1的正方形,//h=2,N/i/8=N/h/O=120°.

(1)求线段ZG的长.

(2)求异面直线ACi与4。所成角的余弦值.

(3)求证:/4_L8D.

请完成课后作业

链接《精练案》分册P75

§11.2用空间向量解决立体几何问题

(对应答案分册第36~39页)

......................圜基础知识……，夯实基础巩固提升

«《知识清单》》

1.直线的方向向量与平面的法向量的确定

(1)直线的方向向量:/是空间一直线,48是直线/上任意两点则称四为直线

/的方向向量，与通平行的任意也是直线/的方向向量，显然一条直线的

方向向量可以有无数个.

(2)平面的法向量

②定义:与平面的向量，称为平面的法向量.一个平面的法向量有无数多

个，任意两个都是共线向量.

②确定:设a,6是平面a内两个不共线向量，〃为平面。的法向量则求法向

量的方程组为｛::二*

2.空间位置关系的向量表示

位置关系向量表示

直线44的方An勿IIni=

向向量分别为

/?L±/72<=>

直线/的方向Zua/7-L/77O-0

向量为〃，平面

a的法向量为/±an\\mon二Am

m

平面a/的法a\\(Snilm<^n=Am

向量分别为

a±/3/7-L777="777=0

n,m

3.空间向量与空间角的关系

(1)两条异面直线所成角的求法(a,6分别为的方向向量)

a与。的夹角

4与人所成的角e

(T

范围(O,TT)

力|

e=/CGS夕n|a

求法8ss不而COS雨

(2)直线和平面所成角的求法

如图所示,设直线/的方向向量为e,平面a的法向量为直线/与平面a所

成的角为夕,两向量e与〃的夹角为8,则有sin(p=/cos勿=辞%

(3)二面角的求法

如图。,/民。是二面角a-//两个半平面内与棱/垂直的直线，则二面角0

的大小为ABCD.

如图②③,/71,柩分别是二面角a-/-£的两个半平面a,£的法向量，则二面角

6的大小满足cos8=或.

4.空间距离

点/在平面a内，点8在平面a外，向量〃为平面a的法向量，则点8到平

面0的距离〃窄.

□特别提醒

关注三种角的易错点

(1)异面直线所成的角与其方向向量

的夹角:当异面直线的方向向量的夹

角为锐角或直角时，就是该异面直线

的夹角;否则向量夹角的补角是该异

面直线所成的角.

(2)直线与平面所成的角:在上述求法

中要注意的是加。二鼎，而不是

cos

(3)二面角与法向量的夹角:利用平面

的法向量求二面角的大小时，当求出

两半平面的法向量小柩时，要

根据向量坐标在图形中观察法向量

的方向，从而确定二面角与向量

力,/72的夹角是相等，还是互补.

夯头基础

【概念辨析】

判断下面结论是否正确.(对的打,错的打"x")

Q)两直线的方向向量的夹角就是两条直线所成的角.()

(2)已知3=(-2,-3,1)力=(2,0,4)(=(4-6,2),则311强_16.()

(3)已知向量分别是直线/的方向向量和平面二的法向量，若cos<m,n>=-

翔直线/与平面a所成的角为120°.()

【对接教材】

2.

如图所示，在棱长为1的正四面体力8。中,£尸分别是力8,力。的中点，贝ij

=；EF-DC=.

如果PA,PB,PC是从氤户出发的三条射线，每两条射线的夹角均为60°,那么直

线PU与平面外8所成角的余弦值为.

【易错自纠】

若直线/的方向向量与平面a的法向量夹角的大小为120°,则直线/与平面a

所成角的大小为().

A.1200B.600

C.30°D.以上均错

已知四二(2,2,1),就二(4,5,3),则平面/8U的单位法向量是

讲考点考向•卜精研考向锤炼技能

利用空间向量证明平行、垂直问题【考向变换】

考向1利用空间向量证明平行问题

初。(一题多解)

如图所示，在正方体/8。-481G中,M/v分别是Gc81G的中点.求

证:例Ml平面48。

一—利用空间向量证明平行的方法

(1)线线平行:证明两直线的方向向量共线.

(2)线面平行:②证明该直线的方向向量与平面的某一法向量垂直;②证明直

线的方向向量与平面内某直线的方向向量平行;③可在平面a内取基向量{a,e},

证明存在实数44,使直线/的方向向量a=尢a+力20,然后说明/不在平面a

内即可.

(3)面面平行:②证明两平面的法向量为共线向量;②转化为线面平行、线线

平行问题.

【追踪训练1］已知在四棱锥"乂8。中，底面力8。是直角梯

形,/必。-90°,2力8=2/。=《。,侧面以。是正三角形且垂直于底面ABCD,E是

PU的中点.试问在所上是否存在一点£使/尸II平面BDR

考向2利用空间向量证明垂直问题

初❷在四棱锥2/8。中，底面力8。为正方形/O_L平面ABCD,E,F分

别为棱户8的中点，且夕。=/。求证:平面CFEL平面PBC.

■利用空间向量证明垂直的方法

(1)线线垂直:证明两直线所在的方向向量互相垂直，即证它们的数量积为零.

(2)线面垂直:证明直线的方向向量与平面的法向量共线，或将线面垂直的判

定定理用向量表示.

(3)面面垂直:证明两个平面的法向量垂直，或将面面垂直的判定定理用向量

表小.

【追踪训练2】如图，在四棱锥中，底面是边长为d的正方

形，侧面外21底面且PA=PD斗AD,设"分别为户的中点.

(1)求证:的I平面PAD.

(2)求证:外，平面PDC.

至利用空间向量求空间角【考向变换】

考向1求异面直线所成的角

剑❸如图，在三棱柱/8U-481G中,881_1平面/8CN必U-90°,£是BC

的中点,/U=/8=/4=2,求异面直线力£与4U所成的角的大小.

用向量法求异面直线所成角的一般步骤

(1)选择三条两两垂直的直线建立空间直角坐标系.

(2)确定异面直线上两个点的坐标，从而确定异面直线的方向向量.

(3)利用向量的夹角公式求出向量夹角的余弦值.

(4)两异面直线所成角的余弦值等于两向量夹角余弦值的绝对值.

□特别提醒

注意向量的夹角与异面直线所

成的角的区别：

当异面直线的方向向量的夹角为锐

角或直角时，就是此异面直线所成的

角;当异面直线的方向向量的夹角为

钝角时，其补角才是异面直线所成的

角.

【追踪训练3】

如图所示，在三棱锥P-/8U中,E4_L平面力81。是棱所的中点，已知

外=8U=2,/8=4,U81./8,贝ij异面直线户所成角的余弦值为().

A乌

A10BT

rV30

D噂

考向2求直线与平面所成的角

幽CJ如图，在四棱锥2/8。中，底面28。是平行四边形,N/8U=60°,侧

面以8JL底面ABCD,^BAP=^Q°,AB=AC=PA=2.

Q)求证:平面户8。，平面PAC.

(2)若例为也的中点,求直线用U与平面28U所成角的正弦值.

:向量法求线面角的两大途径

Q)分别求出斜线和它所在平面内的射影直线的方向向量，转化为求两个方向

向量的夹角(或其补角).

(2)通过平面的法向量来求,即求出斜线的方向向量与平面的法向量所夹的锐

角，取其余角就是斜线与平面所成的角.

【追踪训练4】如图所示，在三棱柱/8U-481G中在平面Z8U

的射影为线段/U的中点。，侧面Z4GU是菱形，平面员8。与棱4G交于点

£

(1)判断四边形881的形状并证明；

(2)求与平面力8员4所成角的正弦的最大值.

B

考向3求平面与平面所成的角

倒疡如图,四棱柱/8UO-481GO1的所有棱长都相

等,/CBD=O,AiGPI814=Q,四边形/CCiAi和四边形BDF员均为矩形.

(1)证明:QOJL底面ABCD.

(2)若NUM=60°,求二面角G-O81-。的余弦值.

」向量法求二面角(或其某个三角函数值)的四个步骤

(1)建立适当的坐标系,写出相应点的坐标；

(2)求出两个半平面的法向量m,/72；

⑶设二面角的平面角为，贝0/=1cos<ni,n2>f,

(4)根据图形判断8为钝角还是锐角，从而求出仇或其三角函数值).

【追踪训练5］如图,四棱锥2/8。中，底面为平行四边

形,ND/8=6O°,/8=2/2Q0_L底面ABCD.

(1)证明:外，8D.

(2)若户。求二面角力-08-0的余弦值.

利用法向量求点到平面的距离【典例迁移】

如图,正方体ABCD-AxBxCiDi的棱长为4,动点户在棱4&上.当AiP^-AiBi

4

时，点C到平面户的距离为

【变式设问】已知长方体ABCD-AiBiCiDi中,48=/。=2,/4=4,£尸分别

为8见。的中点厕点尸到平面的距离为.

^点wvw拨ww*用向量法求点户到平面a的距离的三个步骤

Q)在平面a内取一点4确定向量方的坐标表示；

(2)确定平面a的法向量〃

(3)代入公式4=智求解.

【追踪训练6】'022-在棱长为1的正四面体力8。中，例为

力。上的一点，且/例=豺。,2为/U的中点厕点/到平面8/I4/V的距离为

()-

A.当B日

C包D在

1010

..............................[3方法技巧＞方法探究分类突破

052突破C利用空间向量探究点的位置

£3012•天滓联如图，在四棱锥G/8U。中，平面/8U。，平面

ABE,AB\\CD,ABLBC,AB=2BC=2CD=2,AE=BE=W,M为8F的中点.

(1)求证：。41平面

(2)求二面角G80-U的正弦值.

(3)在线段上是否存在一点2使直线例。与平面8£7V所成角的正弦值

为辟?若存在，求出//V的长;若不存在，说明理由.

E

【突破训练】在三棱锥S-/8U中,281.平面

S4C/SJ_SC/8=L/U=&上为力8的中点，例为CF的中点.

(1)在线段58上是否存在一点/V,使用Ml平面以。若存在,指出点/V的位

置并给出证明;若不存在，说明理由.

(2)若NSC4=30°,求二面角S-UF-8的大小.

B

请完成课后作业

链接《精练案》分册P76

解答题题型突破四立体几何

(对应答案分册第40~42页)

(突破点，立体几何中的翻折问题

把一个平面图形按照某种要求折起，转化为空间图形，进而研究图形在位置关

系和数量关系上的变化，这就是折叠问题.折叠问题是立体几何的一个重要问题，

折叠与展开的转变正是空间几何与平面几何问题转化的集中体现.此类问题是历

年高考命题的一大热点,多涉及空间中的线面关系、体积的求解以及空间角、距

离的求解等问题.

考向1折叠后的线面关系

OO如图②，在平面四边形

中,8。二百/8,。=247,且“18。为等边三角形.设£为力。的中点，连接8£将

△/8£沿折起，使点力到达平面BCDE上方的点E连接PQPD,设厂是ZY■的

中点，连接如图②.

(1)证明:8尸II平面PDE.

(2)若二面角P-BE-D为60°,设平面Q8U与平面ZY汪的交线为/求/与平

面■。所成角的正弦值.

折叠问题要抓住两个关键点:不变的线线关系、不变的数量关系.不变

ZWWVWWX

的线线关系，尤其是平面图形中的线线平行、线线垂直关系是证明空间平行、垂

直关系的起点和重要依据;不变的数量关系是求解几何体的数字特征，如几何体的

表面积、体积、空间中的角与距离等.

【突破训练1】如图,四边形为正方形,£尸分别为

的中点，以。尸为折痕把△。尸U折起，使点U到达点P的位置，且PF1BF.

(1)证明:平面夕日」平面ABFD.

(2)求。户与平面尸。所成角的正弦值.

考向2折叠后几何体的数字特征

蒯❷已知如图。所示，在边长为12的正方形44214中,88111811/4,

且力5=3,8U=4,/Wi分别交88i,UG于点8Q将该正方形沿88i,UG折叠，使

得/2i与重合，构成如图②所示的三棱柱/8U-4员G,在该三棱柱底边

/U上有一点例满足/例=攵⑨。0＜攵＜1),请在图②中解决下列问题：

(1)求证:当左=［时,8/II平面/PQ

(2)若直线8例与平面/PQ所成角的正弦值为唱，求Z的值.

折叠后几何体的数字特征包括线段长度、几何体的表面积与体积、

空间角与距离等.设计问题综合、全面,也是高考命题的重点.解决此类问题的关

键是准确确定折叠后几何体的结构特征以及平面图形折叠前后的数量关系之间

的对应.

【突破训练2】如图,在平行四边形/8W

中,/8=/。=3//。14=90°,以/U为折痕将心。4折起，使点例到达点。的位

置，且

Q)证明:平面平面ABC.

(2)若Q为线段上一点，户为线段8U上一点，且求三棱锥

Q-/89的体积.

【突破点❷立体几何中的探索性问题

探索性问题是相对于那种完全具备条件和固定答案的封闭题而言的,立体几

何探索性试题的条件或结论不完备，要求解答者自己去探索,结合已有条件，进行

观察、分析、比较和概括.它对学生的数学思想、数学意识及综合运用数学方法

的能力提出了较高的要求.它有利于培养学生探索、分析、归纳、判断、讨论与

证明等方面的能力,让学生经历一个发现问题、研究问题、解决问题的全过程.

考向1空间平行关系的探索性问题

施I❸如图，在底面是菱形的四棱锥P-ABCD

中,zABC=60°,PA=AC=a,PB=PD=^a点£在也上，且PE:ED=2:1.

(1)证明:以J■平面/8UO

(2)求二面角的大小.

(3)在棱"C上是否存在一点£使88平面力比?证明你的结论.

平行与垂直关系中探索性问题的类型及解题策略

(1)对命题条件的探索

晚猜后证，即先观察并尝试给出条件，再给出证明；

分通过命题成立的必要条件探索出命题成立的条件，再证明条件的充分性;

③把几何问题转化为代数问题才采索出命题成立的条件.

(2)对命题结论的探索

质索结论是什么，常从条件出发才呆索出要求的结论是什么；

②探索结论是否存在，常先假设结论存在，再在这个假设下进行推理论证，寻

找与条件相符或矛盾的结论，相符则存在，矛盾则不存在.

【突破训练3】如图。，在五边形28次•尸中，△/8尸

为等腰三角形,N班尸=120°,四边形BCEF%矩形,CE=2乘,EF=1,D%"的中

点.将四边形ADEF沿力。折起，使得平面力。9」平面如图②.

图①图②

(1)在2。上是否存在一点E使得平面W国平面力8乃若存在，求出/"的

长;若不存在,请说明理由.

(2)求直线与平面28尸所成角的正弦值.

考向2空间垂直关系的探索性问题

创危!在如图所示的几何体中,四边形。乐为正方形，四边形为等腰

梯形,48llCD,AB=2BC^ABC=^QO,AC1.FB.

(1)求证:/Cl平面FBC.

(2)求直线8U与平面所成角的正弦值.

(3)线段£。上是否存在点Q,使平面E4C1平面Q8a证明你的结论.

点£这类问题的结论已经给定，而需探求此结论成立的条件,常规的解决方

法:执果索因，逆向求索，或合理猜想，再加以证明，即多采用分析法或猜想证明.

【突破训练4】如图，在三棱柱/8U-481G中底面

ABC,AB1.BC,AB=1,BC=2,AAI=<3.

(1)求直线4。与ABi所成角的余弦值；

(2)设例为/U的中点，在平面8UG内找一点N使得例/VJL平面48c求

点/V到平面/8U和平面/881的距离.

考向3空间角的探索性问题

幽疡如图，底面是边长为3的正方形，平面力。£73平面

ABCD,AF\\DE,AD1DE,AF=2瓜,DE=3瓜.

(1)求证:平面平面BED.

(2)求直线C4与平面8匠所成角的正弦值.

(3)在线段/尸上是否存在点M使得二面角股-86。的大小为60°?若存在,

求出券的值;若不存在，说明理由.

R;与空间角有关的探索性问题主要为与两异面直线所成的角、直线与

ZWWWVW*

平面所成的角和二面角有关的存在性问题，常利用空间向量法求解.求解时，一般

把"是否存在"问题转化为"点的坐标是否有解，是否有规定范围内的解"等问

题，并注意准确理解和熟练应用夹角公式.

【突破训练5]如图，在直三棱柱ABC-A1B1C1

中/8/U=90°,/8=/U=2,例为4G的中点,/V为力以上一动点.

(1)是否存在一点/V,使得线段例/Vll平面881Go若存在，指出点/V的位置;

若不存在,请说明理由.

(2)若/V为力员的中点且求二面角M-CN-A的正弦值.

'£\

R_____—2

BC

延展点4空间几何体建系的方法

(对应答案分册第39~40页)

坐标法是利用空间向量的坐标运算解答立体几何问题的重要方法，运用坐标

法解题往往需要建立空间直角坐标系.依据空间几何图形的结构特征，充分利用图

形中的垂直关系或构造垂直关系来建立空间直角坐标系，是运用