机械原理大作业二王志强备用

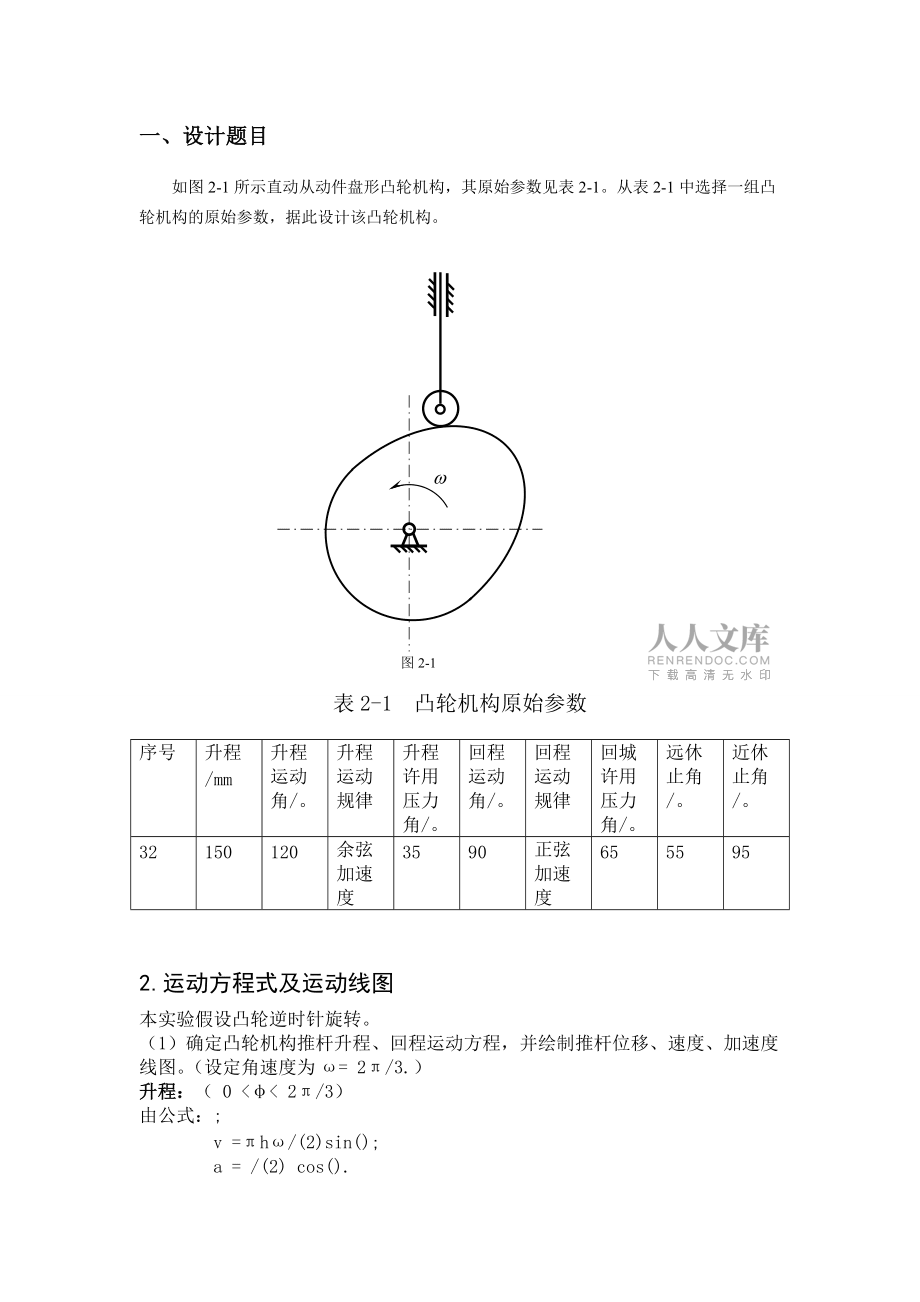
1、Harbin Institute of Technology 机械原理大作业(二)课程名称： 机械原理 设计题目：凸轮机构设计 院 系： 机电学院 班 级： 1208302 设 计 者： 王志强 学 号： 1120830218 指导老师： 焦映厚 设计时间： 2014.6.10 哈尔滨工业大学一、设计题目如图2-1所示直动从动件盘形凸轮机构，其原始参数见表2-1。从表2-1中选择一组凸轮机构的原始参数，据此设计该凸轮机构。图2-1表2-1 凸轮机构原始参数序号升程/mm升程运动角/。升程运动规律升程许用压力角/。回程运动角/。回程运动规律回城许用压力角/。远休止角/。近休止角/。3215012

2、0余弦加速度3590正弦加速度6555952.运动方程式及运动线图本实验假设凸轮逆时针旋转。（1）确定凸轮机构推杆升程、回程运动方程，并绘制推杆位移、速度、加速度线图。（设定角速度为= 2/3.）升程：（ 0 << 2/3）由公式：; v =h/(2)sin(); a = /(2) cos(). 由此得：s = 75*(1 - cos(1.5*);v=0.225/2 * * sin(1.5 *);a = 0.675/4 *2 .* cos(1.5*);回程：（ 35*/36 << 53*/36）由公式 s = h1 T/ + 1/2sin(2T/);v = - h/1

3、cos(2T/);a = -2h sin(2T/) ; T = () 得到s= 0.150*(53/18 - 2*/ + 1/(2*)*sin (4*- 35* /9);v = -0.300/ * * (1 - cos(4*- 35*/9);a = -1.200 *2/*sin(4*- 35* /9);由上述公式通过编程得到位移、速度、加速度曲线如下：（编程见附录）位移运动线图速度运动线图加速度运动线图1. 凸轮机构的线图及基圆半径和偏距的确定凸轮机构的线图如下图所示（代码详见附录）：确定凸轮基圆半径与偏距：见下页：基圆半径为r0 = 142mm，偏距e = 20mm。2. 滚子半径的确定及凸

4、轮理论廓线和实际廓线的绘制得到的理论轮廓曲线为：求其最小曲率半径 = 90.0051这里取半径为 rr= 10mm。程序代码见附录3.凸轮轮廓绘制得到的外包络轮廓，得到图线为：得到的内包络线图为：这里取内包络线图。此即为凸轮的工作轮廓曲线。附录1.求位移、速度、加速度的程序（matlab）w = 2*pi/3x = 0:(pi/100):(2*pi/3);s1 = 75*(1 - cos(1.5*x);v1=0.225/2 * w * sin(1.5 * x);a1 = 0.675/4 * x.2 .* cos(1.5*x);y = (2*pi/3):(pi/100):(35*pi/36);s

5、2 = 150;v2=0;a2 = 0;z = (35*pi/36 ):(pi/100):(53*pi/36);s3 = 0.150*(53/18 - 2*z/pi + 1/(2*pi).*sin (4*z - 35* pi/9);v3 = -0.300/pi * w .* (1 - cos(4*z - 35* pi/9);a3 = -1.200 * z.2/pi .*sin(4*z - 35* pi/9);c = (53*pi/36):(pi/100):( 2*pi);s4 = 0;v4 = 0;a4 = 0;plot(x,s1,'b',y,s2,'b',z,

6、s3,'b',c,s4,'b')plot(x,v1,'g',y,v2,'g',z,v3,'g ',c,v4,'g')plot(x,a1,'r',y,a2,'r',z,a3,'r ',c,a4,'r')xlabel('转角/rad')ylabel('位移/(m/s)')title('位移与转角曲线')2.绘制凸轮机构d/ds s线图x = 0:(pi/100):(2*pi/3);s1 = 7

7、5*(1 - cos(1.5*x);news1 = 75*1.5*sin(1.5*x);y = (2*pi/3):(pi/100):(35*pi/36);s2 = 150;news2 = 0;z = (35*pi/36 ):(pi/100):(53*pi/36);s3 = 150*(53/18 - 2*z/pi + 1/(2*pi).*sin (4*z - 35* pi/9);news3 = 150*(-2/pi + 2/pi *cos(4*z - 35*pi/9);c = (53*pi/36):(pi/100):( 2*pi);s4 = 0;news4 = 0; plot(news1,s1,

8、'b',news2,s2,'b',news3,s3,'b',news4,s4,'b')xlabel('ds/dp');ylabel('(位移s/mm)')title('ds/dp 与位移s曲线')grid3.确定滚子半径（1）.先求凸轮理论轮廓曲线，程序如下：w = 2*pi/3;s0 = 140;s = 150;e = 20;x = 0:(pi/100):(2*pi/3);x1 = (s + s0)*cos(x)-e*sin(x);y1 = (s0 + s)*sin(x) - e*

9、cos(x);y = (2*pi/3):(pi/100):(35*pi/36);x2 = (s + s0)*cos(y)-e*sin(y);y2 = (s0 + s)*sin(y) - e*cos(y);z = (35*pi/36 ):(pi/100):(53*pi/36);x3 = (s + s0)*cos(z)-e*sin(z);y3 = (s0 + s)*sin(z) - e*cos(z);c = (53*pi/36):(pi/100):( 2*pi);x4 = (s + s0)*cos(c)-e*sin(c);y4 = (s0 + s)*sin(c) - e*cos(c);plot(x

10、1,y1,'b',x2,y2,'b',x3,y3,'b',x4,y4,'b');xlabel('x/mm')ylabel('y/mm')title('理轮轮曲线')（2）.求其最小曲率半径，程序如下：v=;syms x1 x2 x3 x4 x5 s0 = 140; e = 20; s1 = 75*(1 - cos(1.5*x1);t1 = (s1 + s0)*cos(x1)-e*sin(x1); y1 = (s0 + s1)*sin(x1) - e*cos(x1); tx1=diff

11、(t1,x1); txx1=diff(t1,x1,2); yx1=diff(y1,x1); yxx1=diff(y1,x1,2);for xx1= 0:(pi/100):(2*pi/3); k1=subs(abs(tx1*yxx1-txx1*yx1)/(tx12+yx12)1.5),x1,xx1); v=v,1/k1;end s2 = 150;t2 = (s2 + s0)*cos(x2)-e*sin(x2); y2 = (s0 + s2)*sin(x2) - e*cos(x2); tx2=diff(t2,x2); txx2=diff(t2,x2,2); yx2=diff(y2,x2); yxx

12、2=diff(y2,x2,2);for xx2=(2*pi/3):(pi/100):(35*pi/36); k2=subs(abs(tx2*yxx2-txx2*yx2)/(tx22+yx22)1.5),x2,xx2); v=v,1/k2;end s3 = 150*(53/18- 2*x3/pi + 1/(2*pi).*sin (4*x3 - 35* pi/9);t3 = (s3 + s0)*cos(x3)-e*sin(x3); y3 = (s0 + s3)*sin(x3) - e*cos(x3); tx3=diff(t3,x3); txx3=diff(t3,x3,2); yx3=diff(y3

13、,x3); yxx3=diff(y3,x3,2);for xx3=(35*pi/36 ):(pi/100):(53*pi/36); k3=subs(abs(tx3*yxx3-txx3*yx3)/(tx32+yx32)1.5),x3,xx3); v=v,1/k3;end s4 = 0;t4 = (s4 + s0)*cos(x4)-e*sin(x4); y4 = (s0 + s4)*sin(x4) - e*cos(x4); tx4=diff(t4,x4); txx4=diff(t4,x4,2); yx4=diff(y4,x4); yxx4=diff(y4,x4,2);for xx4=(53*pi/

14、36):(pi/100):( 2*pi); k4=subs(abs(tx4*yxx4-txx4*yx4)/(tx42+yx42)1.5),x4,xx4); v=v,1/k4;endmin(v)4.绘制凸轮轮廓曲线编程如下：w = 2*pi/3;s0 = 140;e = 20;r = 10;x = 0:(pi/100):(2*pi/3);s1 = 75*(1 - cos(1.5*x);x1 = (s1 + s0).*cos(x) - e*sin(x);y1 = (s0 + s1).*sin(x) - e*cos(x);n1 = -(75*1.5*sin(x) + s0).*sin(x) -e*c

15、os(x);m1 = (s0 + 75*1.5*sin(x) ).*cos(x) + e*sin(x);xt1 = x1+(r*m1)./(sqrt(n1.2+m1.2);yt1 = y1 - (r*n1)./sqrt(m1.2 +n1.2);xw1 = x1 - (r*m1)./sqrt(m1.2 +n1.2);yw1 = y1 + (r*n1)./sqrt(m1.2 +n1.2);y = (2*pi/3):(pi/100):(35*pi/36);s2 = 150;x2 = (s2 + s0).*cos(y)-e*sin(y);y2 = (s0 + s2).*sin(y) - e*cos(y

16、);n2 = -s0.*sin(y)-e*cos(y);m2 = s0 .*cos(y) + e*sin(y);xt2 = x2 + (r*m2)./sqrt(m2.2+n2.2);yt2 = y2 - (r*n2)./sqrt(m2.2+n2.2);xw2 = x2 - (r*m2)./sqrt(m2.2+n2.2);yw2 = y2 + (r*n2)./sqrt(m2.2+n2.2);z = (35*pi/36 ):(pi/100):(53*pi/36);s3 = 150*(53/18 - 2*z/pi + 1/(2*pi).*sin (4*z - 35* pi/9);x3 = (s3 +

17、 s0).*cos(z)-e*sin(z);y3 = (s0 + s3).*sin(z) - e*cos(z);n3 = -(300/pi *cos(4*z - 35*pi/9) + s0).*sin(z)-e*cos(z);m3 = (s0 + 300/pi *cos(4*z - 35*pi/9).*cos(z) + e*sin(z);xt3= x3 + (r*m3)./sqrt(m3.2+n3.2);yt3 = y3 - (r*n3)./sqrt(m3.2+n3.2);xw3 = x3 -(r* m3)./sqrt(n3.2+m3.2);yw3 = y3 + (r*n3)./sqrt(n3

18、.2+m3.2);c = (53*pi/36):(pi/100):( 2*pi);s4 = 0;x4 = (s4 + s0).*cos(c)-e*sin(c);y4 = s0 .*sin(c) - e*cos(c);n4 = - s0.*sin(c)-e*cos(c);m4 = s0 .*cos(c) + e*sin(c);xt4= x4 + (r*m4)./sqrt(m4.2+n4.2);yt4 = y4 - (r*n4)./sqrt(m4.2+n4.2);xw4 = x4 - (r*m4)./sqrt(n4.2+m4.2);yw4 = y4 + (r*n4)./sqrt(n4.2+m4.2);plot(xt1,yt1,'b',xt2,yt2,'b',xt3,yt3,'b',x