2-2直线的投影@

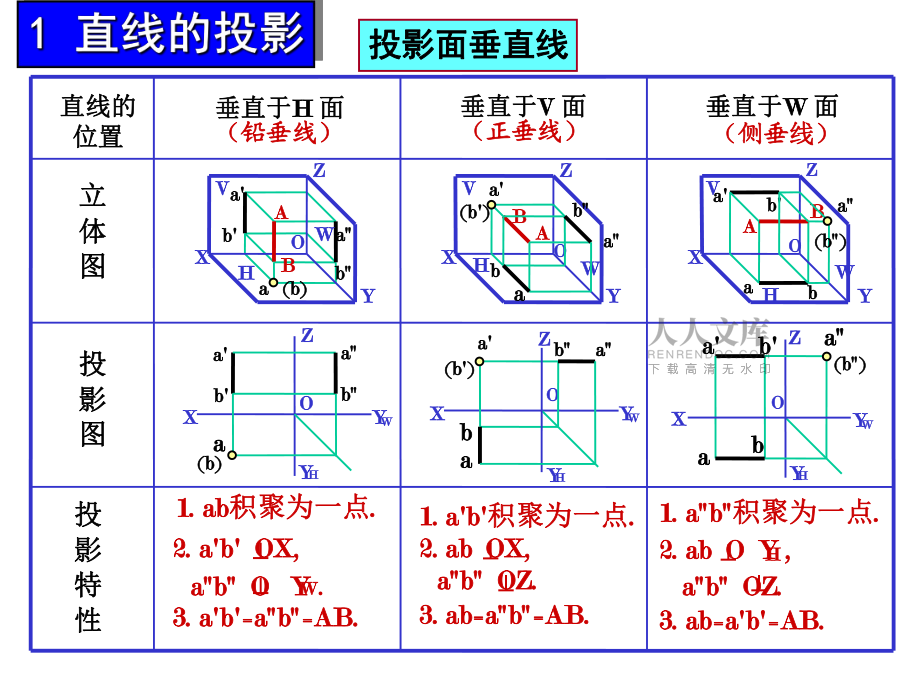
1、 1 1 直线的投影直线的投影 3 3 两直线的相对位置两直线的相对位置 4 4 一边平行于投影面的直角一边平行于投影面的直角的投影的投影目录 2 2 直线上的点直线上的点aabbb ba aV VWWHHZ ZX XO OY YV VZ ZX XY YO OWWHHA AB Bbbaaa ab bb ba aHHWWV VO OZ ZY YX X1. ab1. ab积聚为一点积聚为一点. .3. a3. ab b=ab=AB.=ab=AB.1. a1. ab b积聚为一点积聚为一点. .3. ab=ab=AB.3. ab=ab=AB.1. ab1. ab积聚为一点积聚为一点. .3. ab=

2、a3. ab=ab b=AB.=AB.投影面垂直线投影面垂直线立立 体体 图图投投 影影 图图投投 影影 特特 性性直线的直线的 位置位置垂直于垂直于H H 面面（铅垂线铅垂线）垂直于垂直于V V 面面（正垂线正垂线） 垂直于垂直于W W 面面 （侧垂侧垂线）线）Y YHHZ Zb bX Xa aY YO Oa a(b)(b)WWaabbA AB B2. ab OX,2. ab OX, ab OZ.ab OZ.HH2. ab O Y ,2. ab O Y , ab OZ.ab OZ.WW2. a2. ab b OX, OX, ab O Yab O Y .A AB BY YZ ZO OX Xa

3、a(b(b) )b ba aaabbHHY YWWa a (b)(b)a a(b(b) )Y YHHO O(b)(b)aaX Xb ba ab ba aZ ZY YWW(b)(b)aa投影面垂直线a ab b投影面平行线投影面平行线1. ab=AB;1. ab=AB;a ab b OZ. OZ.2. ab OY ,2. ab OY , H H1. a1. ab b=AB;=AB;2. ab OX,2. ab OX, ab OZ.ab OZ.1. ab=AB1. ab=AB; ;2. a2. ab b OX OX ab OYab OYWW . .O OZ ZY YHHb baaa aa ab b

4、X XY YWWbbX XY YWWa ab ba ab baabbZ ZY YHHO O立立 体体 图图投投 影影 图图投投 影影 特特 性性直线的直线的 位置位置平行于平行于H H 面面（水平线水平线）平行于平行于V V 面面（正平正平线）线） 平行于平行于W W 面面 （侧平线侧平线）Z ZV VY YX XO OHHWWbbaaa ab ba ab bZ ZV VX XY YO OHHWWa ab bb ba aA AB Ba ab bZ ZV VX XY YHHWWO Oa ab bbbaaA AB BaabbY YHHY YWWX Xb ba aaaa ab bZ ZO ObbA

5、AB B投影面平行线A AB BC CD DE E(F)(F) 例例 判断形体中的轮廓线与投影面的相对位置判断形体中的轮廓线与投影面的相对位置a ad db bc cd dbbc ce(f)e(f)b b(e (e) )c c(f (f) )a(e)a(e)d(f)d(f)a aEFEF是铅垂线是铅垂线CFCF是正垂线是正垂线DFDF是侧垂线是侧垂线CDCD是水平线是水平线ADAD是正平线是正平线BCBC是侧平线是侧平线例一般位置直线一般位置直线 1. 与三个投影面都倾斜的直线称为与三个投影面都倾斜的直线称为一般位置直线一般位置直线。 2. 投影特性：三个投影长度均小于实长，并倾斜于投影投影特

6、性：三个投影长度均小于实长，并倾斜于投影轴，且不反映与投影面的倾角。轴，且不反映与投影面的倾角。(直线与直线与H H面的倾角记为面的倾角记为 , ,与与V V面的倾角记为面的倾角记为 , ,与与W W面的倾角记为面的倾角记为 。) ) a ab bbbaaa ab bB BA Ao oZ ZX XY YV VWWHHHHY YZ ZX Xo oWWY Ya aa ab bb bbbaa一般线用用直角三角形法直角三角形法求求一般位置一般位置 直线直线的的实长实长 以以H H（V V、W W）投影）投影长为一直角边，两端点长为一直角边，两端点的的Z Z（Y Y、X X）坐标差为）坐标差为另一直角边

7、，作一直角另一直角边，作一直角三角形，则斜边长为实三角形，则斜边长为实长。长。a ab bbbaaa ab bB BA Ao oZ ZX XY YV VWWHHHHY YZ ZX Xo oWWY Y实 长a aa ab bb bbbaaH投影长实 长Y YY YX X X X实 长Z ZZ Z直角三角形的构成：直角三角形的构成：投影长、坐标差、倾角、投影长、坐标差、倾角、实长。实长。直角三角形法a a b b a ab b直线上的点直线上的点直线上的点直线上的点的投影，一定落在该直线的同面投影上。直线上的点的投影，一定落在该直线的同面投影上。o oZ ZX XY YV VWWHHA AB Ba

8、 ab bb ba ac c c c一直线上两线段长度之比，等于它们的投影长度之比。一直线上两线段长度之比，等于它们的投影长度之比。AC:CB=ac:cb=aAC:CB=ac:cb=ac c:c :c b bC Cc cc co oZ ZX XY YV VWWHH例：直线上取点直线上的点直线上的点 例例 在在AB线上求一点线上求一点C，使点，使点C与与V、H等距。等距。a ab ba ab bb ba ab bA AB Bbbaaa aaabbc cc c 作作V-HV-H平面的分角面（此面垂直于平面的分角面（此面垂直于W W面，积聚为一条面，积聚为一条4545线，面上所有的点均与线，面上所有

9、的点均与V V、H H等距），求出等距），求出ABAB的的W W投影与此投影与此4545线的交点即得。线的交点即得。c c4545c c分角面分角面与与H面面距离距离与与V面面距离距离c cc cC C 两直线平行两直线平行a a b bd dc cX XO Oa ab bd dc ca ab bd dc cD DA AC CB Ba ab bc cd dHHV VO OX X 空间平行两直线，空间平行两直线，其同面投影仍互相平其同面投影仍互相平行。行。 反之，若两直线的反之，若两直线的同面投影同面投影都都互相平行，互相平行，则这两直线平行。则这两直线平行。 判断两条一般线是否判断两条一般线是

10、否平行，要画全它们的三面投平行，要画全它们的三面投影。当且仅当，其三面投影影。当且仅当，其三面投影分别平行，才能判断两直线分别平行，才能判断两直线在空间处于平行状态。否则，在空间处于平行状态。否则，两直线不平行。两直线不平行。ABAB CDCDabab cdcd; ; a ab b c cd d e ef fe ee ef ff fm mm mn nn nmmnnX XO OY YY YZ ZWWHHEF EF MNMN? ?EFEF MNMN两直线平行 两直线相交两直线相交相交两直线，其同相交两直线，其同面投影均相交，且面投影均相交，且交点的连线垂直于交点的连线垂直于投影轴。投影轴。反之，反

11、之，若两直线的同面投若两直线的同面投影均相交，影均相交，且交点的连线且交点的连线垂直于投影轴，则垂直于投影轴，则两直线两直线相交。相交。若两直线中有一条为某一若两直线中有一条为某一投影面的平行线，则应利投影面的平行线，则应利用第三投影来进行判断。用第三投影来进行判断。( (本例中本例中和和点不是交点，点不是交点，因此，因此，AB与与CD不相交。不相交。) )A AB Bb ba aa ab bc cd dc cd dX XO Oa ab ba ab bc cd dc cd dHHV VO OX XC CD DK Kk k k kk kk ka ab ba aaabbb bX XO OY YY

12、YZ ZWWHHc cd dc cd dc cdd AB与与CD不相交不相交两直线相交两直线交叉 两直线交叉两直线交叉既不平行、也不相交的两直线称为既不平行、也不相交的两直线称为交叉两直线交叉两直线。交叉二直线的同面投影可能平行，但不可能所有同面投交叉二直线的同面投影可能平行，但不可能所有同面投影都平行；其同面投影可能相交，但交点连线不垂直于影都平行；其同面投影可能相交，但交点连线不垂直于投影轴。投影轴。b ba aa ab bc cd dc cd dV VHHO OX XA AB BD DC CF FE Ee e(f)(f)g g(j (j) )G GJ J重影点 两直线交叉两直线交叉 比较

13、相邻投影两点的坐标大小，坐标大比较相邻投影两点的坐标大小，坐标大的可见，坐标小的不可见。的可见，坐标小的不可见。Y YG G Y YJ Jg g可见可见j j不可见不可见Z ZE E Z ZF Fe e可见可见f f不可见不可见g g(j (j) )c cd dd dc cb ba aa ab bO OX Xg gj je e(f)(f)e ef f重影点重影点重影点重影点重影点的可见性判断重影点的可见性判断：b ba aa ab bc cd dc cd dV VHHO OX XA AB BD DC CF FE Ee e(f)(f)g g(j (j) )G GJ J重影点重影点：分属两直线的两

14、个点在某投影面上的重合投影叫重影点。：分属两直线的两个点在某投影面上的重合投影叫重影点。 两直线垂直两直线垂直空间两直线空间两直线相交（或交叉）垂直相交（或交叉）垂直，当一直线（或两直线）平，当一直线（或两直线）平行于某投影面时，它们在该投影面上的投影才反映直角。行于某投影面时，它们在该投影面上的投影才反映直角。反之，反之，若两直线在某投影面上的投影为直角，而且其中一条若两直线在某投影面上的投影为直角，而且其中一条直线平行于该投影面，则这两条直线在空间一定相互垂直。直线平行于该投影面，则这两条直线在空间一定相互垂直。X XO OV VHHO OX Xc cC Cc ca ab ba ab bB

15、 BA Ac cc cb bb ba aa ac c1 1b b1 1( (c c1 1) )B B1 1C C1 1(b)(b)c c1 1b b1 1(c)(c)(b)(b)ABAB与与BCBC相交垂相交垂直直ABAB与与B B1 1C C1 1交叉垂交叉垂直直两直线垂直例例 判断下列各题的两直线是否垂直（相交或交叉）。判断下列各题的两直线是否垂直（相交或交叉）。（相交不垂直）（相交不垂直）c cd dd dc cX XO Oa aa ab bb bO OX Xa ab ba ab bc cd dc cd da ab ba ab bd dc cc cd dX XO Oa ab ba ab bX XO Oc cd dc cd d（交叉垂直交叉垂直）（交叉垂直）（交叉垂直）（相交