武汉理工大学2013第一学期概率论与数理统计期末考试试题及答案

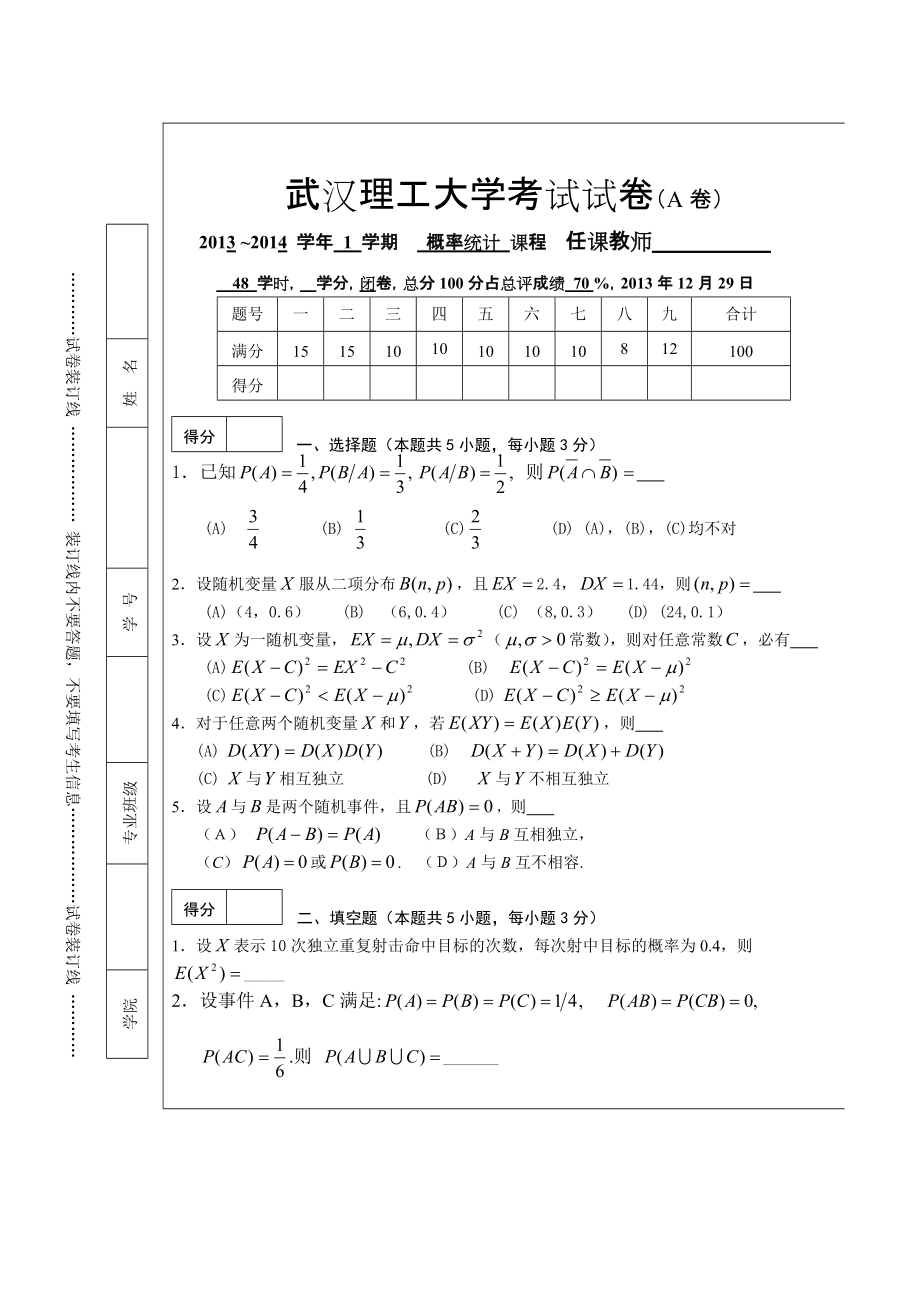
1、 试卷装订线 装订线内不要答题，不要填写考生信息试卷装订线 姓 名学 号专业班级学院武汉理工大学考试试卷（A卷）2013 2014 学年 1 学期 概率统计 课程 任课教师 48 学时， 学分，闭卷，总分100分占总评成绩 70 %，2013年12月29日题号一二三四五六七八九合计满分15151010101010812100得分得分一、选择题（本题共5小题，每小题3分）1已知 则 (A) (B) (C) (D) (A)，(B)，(C)均不对2设随机变量服从二项分布，且2.4，1.44，则 (A)（4，0.6） (B) （6,0.4） (C) （8,0.3） (D) (24,0.1）3设为一随机

2、变量，（常数），则对任意常数，必有 (A) (B) (C) (D) 4对于任意两个随机变量和，若，则 (A) (B) (C) 与相互独立 (D) 与不相互独立5设与是两个随机事件，且，则 （） （）A与B互相独立，（C）或. （）A与B互不相容. 得分二、 填空题（本题共5小题，每小题3分）1设表示10次独立重复射击命中目标的次数，每次射中目标的概率为0.4，则_ 2设事件A，B，C满足: .则 _ 3设随机变量X服从正态分布，且，则_4设是来自总体的一个样本，的概率密度为：，则的矩估计为_5已知一批零件的长度X (单位：cm)服从正态分布，从中随机地抽取9个零件，得到样本均值 (cm)，则的

3、置信度为0.95的置信区间是 _ , . 得分三、 （本题10分）1（5分）假设，若与相互独立，试求2（5分）设，试求得分四、 （本题10分）已知一批产品90%是合格品，检查产品时，一个合格品被误认为次品的概率为0.02，而一个次品被误认为合格品的概率为0.05。求：（1）检查一个产品被认为合格品的概率；（2）被认为合格品的产品确实合格的概率。得分五、 （本题10分） 设随机变量相互独立, 其概率密度分别为：求 (1)的联合概率密度(2) ；(3)随机变量的分布函数及概率密度. 得分六、 （本题10分） 设二维随机变量的联合密度函数为： （1）求常数A ；（2）求及协方差；（3）说明与的相关性

4、.试卷装订线 装订线内不要答题，不要填写考生信息试卷装订线 试卷装订线 装订线内不要答题，不要填写考生信息试卷装订线 七、 （本题10分）设总体的概率分布为： 1 2 3 其中是未知参数，已知取得了样本值，求的矩估计值和最大似然估计值。得分八、 （本题8分）设某次考试的学生成绩服从正态分布，从中随机地抽取36位考生的成绩，算得样本均值分，样本方差分，问在显著性水平0.05下，是否可以认为这次考试全体考生的平均成绩为70分？并给出检验过程。（ ， ）得分九（本题12分）设随机变量只取一个值，（1）求的分布函数。（2）证明：与任意的随机变量相互独立。武汉理工大学考试试题答案（A卷）2013 2014 学年 1 学期 概率统计 课程一、C B D B A二、（1）18.4 （2） （3） （4） （5）（4.412，5.588） 三、1、解： 。 5分 2、解： 5分四解：设为产品合格事件，则是产品的一个划分。又设B为产品检查合格事件，则，。 （1） 由全概率公式，一个产品被认为合格的概率。 6分（2）由贝叶斯定理，“合格品”确实合格的概率 10分五解：（1）联合密度为 .3分(1) 6分(3) 当时，当时， 当时， 8分 10分六解：（1）由，得1 2分（2） 6分 8分 （3） 与不相关 10分七解：（1），的矩估计值为： 5分（2）， 的最大