勾股定理教案设计

1、勾股定理教案设计学院：数学与统计学院班级：2010级数学（2）班姓名：南宫天浪勾股定理教案设计【教材分析】（一）教材来源：新课标人教版初中数学八年级下册第十八章。（二）教材地位与作用：勾股定理在中国又称为“商高定理”，在外国称为“毕达哥拉斯毕达。学生通过对本节内容为学习勾股定理逆定理作铺垫，为学习“四边形”和“解直角三角形”奠定基础，可以在原有的基础上对直角三角形有进一步的认识和理解。【教学目标】一、 知识与技能角度1. 体验勾股定理的探索过程，了解利用拼图验证勾股定理的方法；利用勾股定理解决日常生活中的简单问题；2. 培养学生“观察-比较-分析-推理-概括”的能力，在探索过程中，体会数形结合

2、思想。二、过程与方法角度在方格纸上通过计算面积的方法探索勾股定理的活动；同时又安排了用拼图的方法验证勾股定理的内容。三、态度、情感与价值观1.培养学生积极参与，合作交流的意识；2.探究勾股定理的过程中体验解决问题方法的多样性，体验快乐，激发学习的兴趣；3.通过简单的了解勾股定理的历史，增强学生爱国情怀。【教学重点】1.用面积法探索勾股定理，掌握并理解勾股定理；2.灵活运用勾股定理。【教学难点】用拼图法证明勾股定理。【教学方法】1.学情分析：八年级学生已经具备一定的观察、归纳、猜想和推理的能力。已经掌握了通过分割、拼接法计算一些几何图形的面积,但运用面积法和割补思想来解决问题的意识和能力还不够。

3、另外，学生普遍学习积极性较高，课堂活动参与较主动，但合作交流的能力还有待加强。2.学法分析：在教师的组织引导下，采用自主探索、合作交流的学习方式，让学生获取知识，掌握方法，借此培养学生动手、动脑、动口的能力，使学生真正成为学习的主体。【教学用具】正方形网格纸，多媒体设备及必要设备等。【教学过程】针对八年级学生的知识结构和心理特征，本节课选择引导探索法，由浅入深，由特殊到一般地提出问题，进行教学。教学过程的流程入下：反馈练习，巩固新知创设情境，引入课题自主探索，合作交流验证猜想，得到定理总结反思，提炼精华安排作业，课堂延伸一、创设情境，引入课题2500年前，古希腊著名的哲学家、数学家、天文学家毕

4、达哥拉斯有一次去朋友家做客时，发现朋友家的用砖铺成的地面中地砖上的三个正方形存在某种数学关系。图1图2图3图1是黑白相间的地砖，教师引导学生观察图2、图3中两个红色小正方形与蓝色大正方形有什么关系？二、自主探索，合作交流活动过程：Ø 按照相邻原则进行分组，选组长；Ø 活动过程中，要求大家踊跃讨论，组长回答老师提问；Ø 讨论结束后，教师利用多媒体设备进行活动演示，以对学生的探究结果进行论证。1.探究活动一：等腰直角三角形三边关系图4是单位面积为1的正方形组成的，请你数一数图4.1、图4.2、图4.3中正方形A、B、C各占几个格子？计算正方形面积，完成表格1，并探究规

5、律。图4.1图4.2图4.3图4正方形A面积正方形B面积正方形C面积图4.1图4.2图4.3探究正方形A，B， C之间面积关系总结等腰直角三角形三边关系表1探究活动结束后，教师要求各组长发言，说明他们组的讨论结果。最后师生互动得出等腰直角三角形三边关系，那么任意直角三角形三边关系会不会有这样的关系了？2.探究活动二：任意直角三角形三边关系仿照探究活动一的方法，请你数一数图5.1、图5.2中正方形A、B、C各占几个格子？计算正方形面积，完成表格2，并探究规律。图 5.1图 5.2图 5正方形A面积正方形B面积正方形C面积图4.1图4.2图4.3探究正方形A，B， C之间面积关系总结任意直角三角形

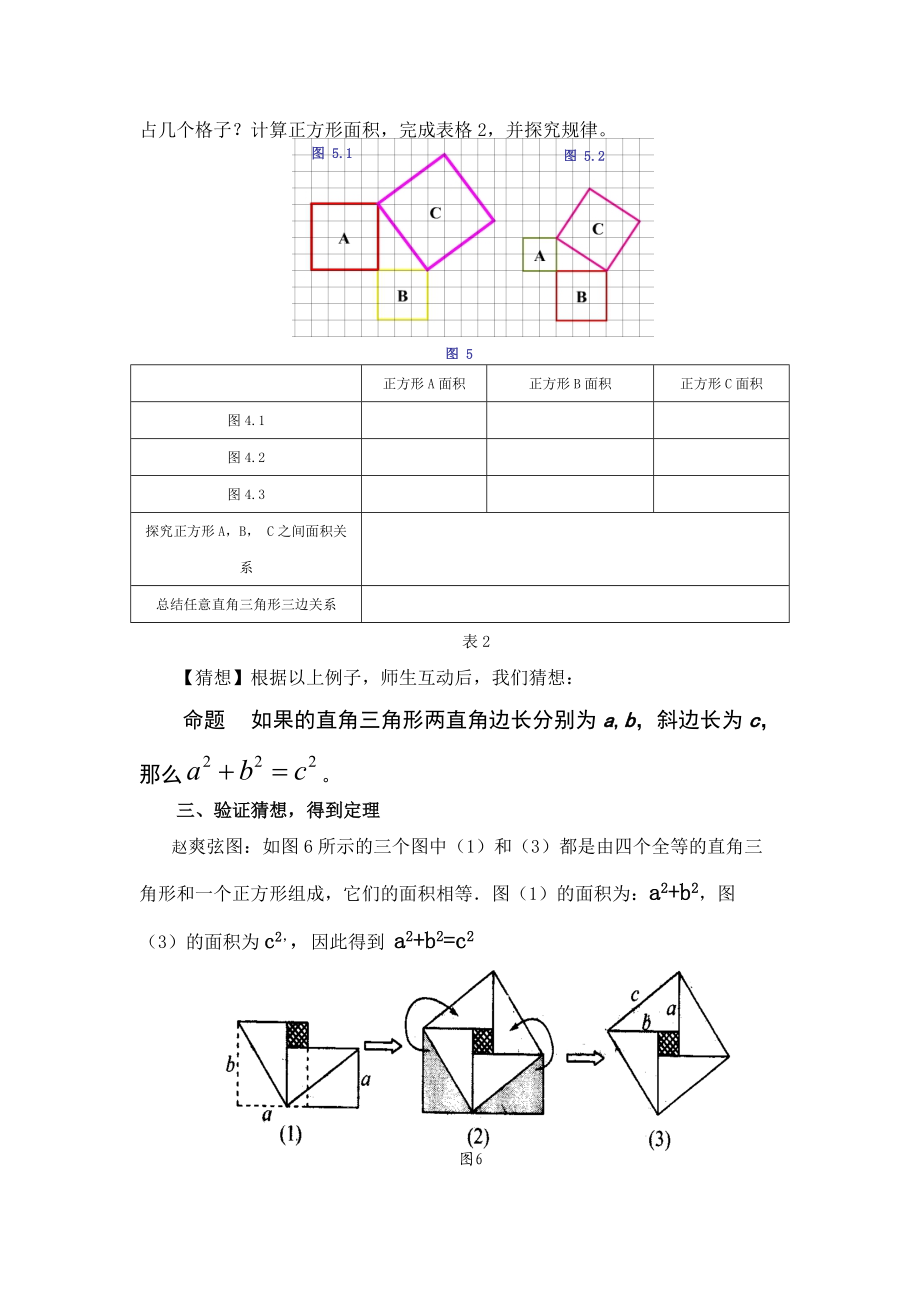
6、三边关系表2【猜想】根据以上例子，师生互动后，我们猜想：命题 如果的直角三角形两直角边长分别为a,b，斜边长为c，那么。三、验证猜想，得到定理赵爽弦图：如图6所示的三个图中（1）和（3）都是由四个全等的直角三角形和一个正方形组成，它们的面积相等图（1）的面积为：a2+b2，图（3）的面积为c2，因此得到 a2+b2=c2图6经过证明命题是正确的，则：勾股定理： 在一个直角三角形中，两直角边的平方和等于斜边的平方。四、反馈练习，巩固新知实践应用一：应用定理1.在ABC中，C=90°。若a=6，b=8，则c= 。 2.若直角三角形中，有两边长是3和4，则第三边长的平方为（ ）A 25 B

7、 14 C 7 D 7或25实践应用二：探索情境例1.如图6所示，一棵大树在一次强烈台风中于离地面9米处折断倒下，树顶落在离树根12米处.大树在折断之前高多少？129图 6五、总结反思，提炼精华Ø 你这节课的主要收获是什么？Ø 该定理揭示了哪一类三角形中的什么元素之间的关系？Ø 在探索和验证定理的过程中，我们运用了哪些方法？Ø 你最有兴趣的是什么？你有没有感到困难的地方？ Ø 反思本节课的学习你参与了讨论了吗？新知识的学习你检测的结果如何？六、安排作业，课堂延伸为了进一步巩固新知识，特此安排以下作业：1.习题1.1 1，2，3，4。2. 思考题：在平静的