新人教版九年级数学上册旋转电子版教案

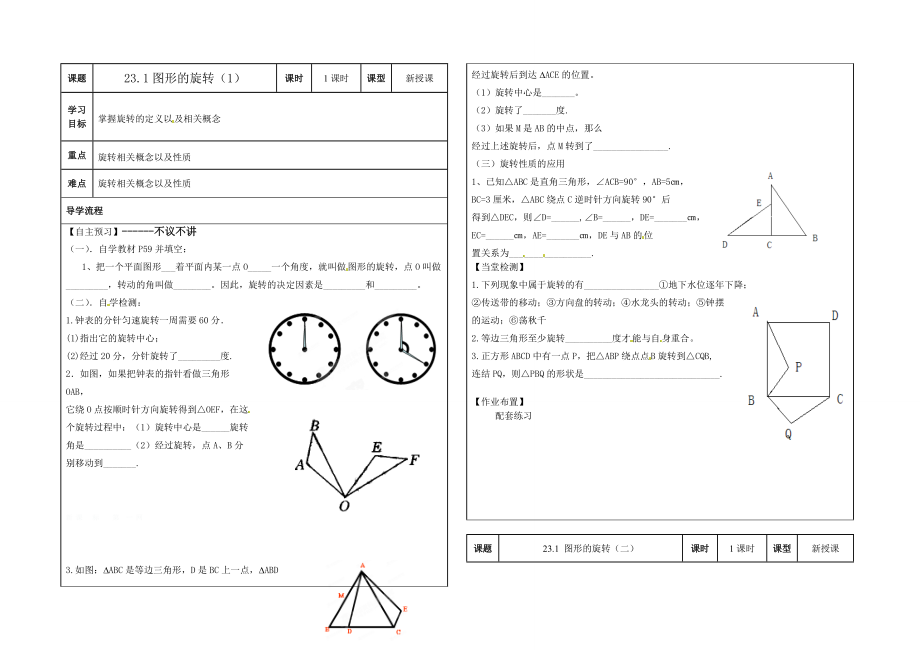
1、课题23.1图形的旋转（1）课时1课时课型新授课学习目标掌握旋转的定义以及相关概念 重点旋转相关概念以及性质难点旋转相关概念以及性质导学流程【自主预习】-不议不讲（一）自学教材P59并填空：1、把一个平面图形_着平面内某一点O_一个角度，就叫做图形的旋转，点O叫做_，转动的角叫做_。因此，旋转的决定因素是_和_。（二）自学检测：1.钟表的分针匀速旋转一周需要60分(1)指出它的旋转中心；(2)经过20分，分针旋转了_度.2如图，如果把钟表的指针看做三角形OAB，它绕O点按顺时针方向旋转得到OEF，在这个旋转过程中：（1）旋转中心是_旋转角是_（2）经过旋转，点A、B分别移动到_.新 课 标 第

2、 一 网3.如图：DABC是等边三角形，D是BC上一点，DABD经过旋转后到达DACE的位置。（1）旋转中心是_。（2） 旋转了_度.（3）如果M是AB的中点，那么经过上述旋转后，点M转到了_.（三）旋转性质的应用X|k | B| 1 . c|O |m1、 已知ABC是直角三角形，ACB=90°，AB=5，BC=3厘米，ABC绕点C逆时针方向旋转90°后得到DEC，则D=_,B=_，DE=_，EC=_，AE=_，DE与AB的位置关系为_. 【当堂检测】1.下列现象中属于旋转的有_地下水位逐年下降；传送带的移动；方向盘的转动；水龙头的转动；钟摆的运动；荡秋千2.等边三角形至少

3、旋转_度才能与自身重合。3.正方形ABCD中有一点P，把ABP绕点点B旋转到CQB,连结PQ，则PBQ的形状是_.【作业布置】 配套练习 课题23.1 图形的旋转（二）课时1课时课型新授课学习目标 理解对应点到旋转中心的距离相等；理解对应点与旋转中心所连线段的夹角等于旋转角；理解旋转前、后的图形全等掌握以上三个图形的旋转的基本性质的运用重点图形的旋转的基本性质及其应用难点运用操作实验几何得出图形的旋转的三条基本性质导学流程新|课 |标|第 |一| 网【旧知回顾】学生口答 1什么叫旋转？什么叫旋转中心？什么叫旋转角？ 2什么叫旋转的对应点？【自主预习】-不议不讲1、 探究新知X k B 1 .

4、c o m 大家在硬纸板上，挖一个三角形洞，再挖一个小洞O作为旋转中心，硬纸板下面放一张白纸先在纸上描出这个挖掉的三角形洞（ABC），然后围绕O转动硬纸板，再描出这个挖掉的三角形洞（ABC），移开硬纸板，请大家运用刻度尺和量角器度量线段和有关角，并探索旋转的性质（分组讨论）根据图回答下面问题（一组推荐一人说明） 1线段OA与OA，OB与OB，OC与OC有什么关系？ 2AOA，BOB，COC有什么关系？ 3ABC与ABC形状和大小有什么关系？二、总结归纳：旋转的性质（1）对应点到旋转中心的距离相等；（2）对应点与旋转中心所连线段的夹角等于旋转角；（3）旋转前、后的图形全等三、例题 如图，E是正方

5、形ABCD中CD边上任意一点，以点A为中心，把ADE顺时针旋转90度，画出旋转后的图形。【当堂检测】1.画出ABC绕点D顺时针旋转90°后的图形A1B1C1ABC绕点D顺时针旋转后的图形为A1B1C1，找出旋转中心点D。D2.如果两个图形可通过旋转而相互得到，则下列说法中正确的有( )对应点连线的中垂线必经过旋转中心这两个图形大小、形状不变对应线段一定相等且平行将一个图形绕旋转中心旋转某个定角后必与另一个图形重合A1个 B2个 C3个 D4个【作业布置】 课本第62页第三、四题课题 中心对称课时1课时课型新授课学习目标了解中心对称、对称中心、关于中心的对称点等概念及掌握这些概念解决一

6、些问题重点利用中心对称、对称中心、关于中心对称点的概念解决一些问题难点从一般旋转中导入中心对称X|k | B| 1 . c|O |m考点利用中心对称、对称中心、关于中心对称点的概念解决一些问题导学流程【自主预习】-不议不讲一、探究新知（一） w W w .x K b 1.c o M (1)把其中一个图案绕点O旋转180°,你有什么发现? (2)线段AC,BD相交于点O,OA=OC,OB=OD.把 OCD绕点O旋转180°,你有什么发现? 总结归纳： 像这样把一个图形绕着某一点旋转180度,如果它能够和 另一个图形重合,那么,我们就说这两个图关于这个点对称或中心对称,这个点就

7、叫对称中心,这两个图形中的对应点,叫做关于中心的对称点.探究新知（二） 旋转三角板，画关于点O对称的两个三角形：第一步，画出ABC；第二步，以三角板的一个顶点O为中心，把三角板旋 转180°，画出ABC；第三步，移开三角板.思考：画出的ABC与ABC关于点O对称.分别连接对称点AA、BB、CC。点O在线段AA上吗？如果在，在什么位置？ ABC与ABC有什么关系？总结归纳： （1）在成中心对称的两个图形中,连接对称点的线段都经过对称中心,并且被对称中心平分.反过来,如果两个图形的对应点连成的线段都经过某一点,并且都被该点平分,那么这两个图形一定关于这一点成中心对称.（2）关于中心对称的

8、两个图形是全等形。二、灵活运用，体会内涵1、点的中心对称点的作法 以点O为对称中心,作出点A的对称点A;2、线段的中心对称线段的作法以点O为对称中心,作出线段AB的对称线段点AB3/如图,选择点O为对称中心,画出与ABC关于点O对称的ABC。 【当堂检测】w W w .X k b 1. c O m 一、选择题 1下面图形中既是轴对称图形又是中心对称图形的是（ ） A直角 B等边三角形 C直角梯形 D两条相交直线 2下列命题中真命题是（ ） A两个等腰三角形一定全等 B正多边形的每一个内角的度数随边数增多而减少 C菱形既是中心对称图形，又是轴对称图形 D两直线平行，同旁内角相等 3将矩形ABCD

9、沿AE折叠，得到如图的所示的图形，已知CED=60°，则AED的大小是（ ）A60° B50° C75° D55° 二、填空题 1关于中心对称的两个图形，对称点所连线段都经过_，而且被对称中心所_ 2关于中心对称的两个图形是_图形 3线段既是轴对称图形又是中心对称图形，它的对称轴是_，它的对称中心是_ 三、综合提高题新|课 |标|第 |一| 网 1分别画出与已知四边形ABCD成中心对称的四边形，使它们满足以下条件：（1）以顶点A为对称中心，（2）以BC边的中点K为对称中心 2如图，已知一个圆和点O，画一个圆，使它与已知圆关于点O成中心对称 【作

10、业布置】 课本P69第一题课题 中心对称图形课时1课时课型新授课学习目标了解中心对称图形的概念及中心对称图形的对称中心的概念，掌握这两个概念的应用重点中心对称图形的有关概念及其它们的运用难点区别关于中心对称的两个图形和中心对称图形考点区别关于中心对称的两个图形和中心对称图形导学流程w W w .x K b 1.c o M【旧知回顾】-不练不讲1.关于中心对称的两个图形具有什么性质？2（学生活动）作图题（1）作出线段AO关于O点的对称图形，如图所示（2） 作出三角形AOB关于O点的对称图形，如图所示 【自主预习】-不议不讲 一、探究新知 议一议： （1）这些图形有什么共同的特征？ （2）这些图形

11、的不同点在哪？分别绕旋转中心旋转了多少度?2、 总结归纳： 如果一个图形绕一个点旋转 后，能和原来的图形互相 ，那么这个图形叫做中心对称图形；这个点叫做它的对称中心；互相重合的点叫做对称点. 3、 例题讲解ABCDFEO如图，点O是平行四边形的对称中心，点A、C关于点O对称，有AO=CO，那么OE=OF吗？新|课 |标|第 |一| 网【当堂检测】1、下列命题中的真命题是( )A、全等的两个图形是中心对称图形. B、关于中心对称的两个图形全等.C、中心对称图形都是轴对称图形. D、轴对称图形都是中心对称图形.2、下列图形中，既是轴对称图形又是中心对称图形的是（ ）A、 B、 C、 D、3下面是两

12、个圆，请按要求在各图中分别添加四个点，使之满足各自要求 (1)既是中心对称图形， (2)只是中心对称图形，又是轴对称图形 不是轴对称图形 【作业布置】 课本P41第五题（2）课题 关于原点对称的点的坐标课时1课时课型新授课学习目标理解点P与点P关于原点对称时，它们的横纵坐标的关系，掌握P（X,Y）关于原点的对称点为P（-X,-Y）的运用；重点掌握P（X,Y）关于原点的对称点为P（-X,-Y）的运用；难点掌握P（X,Y）关于原点的对称点为P（-X,-Y）的运用；w W w .X k b 1. c O m考点掌握P（X,Y）关于原点的对称点为P（-X,-Y）的运用；导学流程【旧知回顾】-不练不讲1.什么是平面直角坐标系？2.怎样在平面直角坐标系内表示一个点的坐标？3.点P(a,b)关于x轴的对称点的坐标 ，关于y轴对称点 坐标是 。4.点P(2,3)关于x轴的对称点的坐_关于Y轴的对称点的坐标是_.5.点M(-3,-4)在第_象限,点M到x轴的距离是_,到Y轴的距离是_,ABCDEF5-5-2-3-4-13241-55-3-44-23-121o 原点的距离是_.【自主预习】-不议不讲1、 探究新知 如图，在直角坐标系中，已知A（-3,1）、B（-4,0）、C（0,3）、D（2,2）、E（3,-3）、F(-2,-2)，作出A、B、C、D、E、F点关于原点O的中心对称点，并写出它们的