正弦定理 (3)

1、正弦定理、余弦定理正弦定理、余弦定理赵艳赵艳正弦定理正弦定理回忆一下直角三角形的边角关系回忆一下直角三角形的边角关系? ABCcba222cba Acasin Bcbsin Abatan 90BA两等式间有联系吗？两等式间有联系吗？cBbAa sinsin1sin CCcBbAasinsinsin 对任意三角形对任意三角形, , 以上关系是否成立以上关系是否成立? ? A c h bB a D CCcBbCbBchBCADsinsinsinsin 即：即：，则，则如图：作如图：作正弦定理正弦定理在锐角在锐角 中，中，ABC AbcBacCabahSABCsin21sin21sin2121 又：

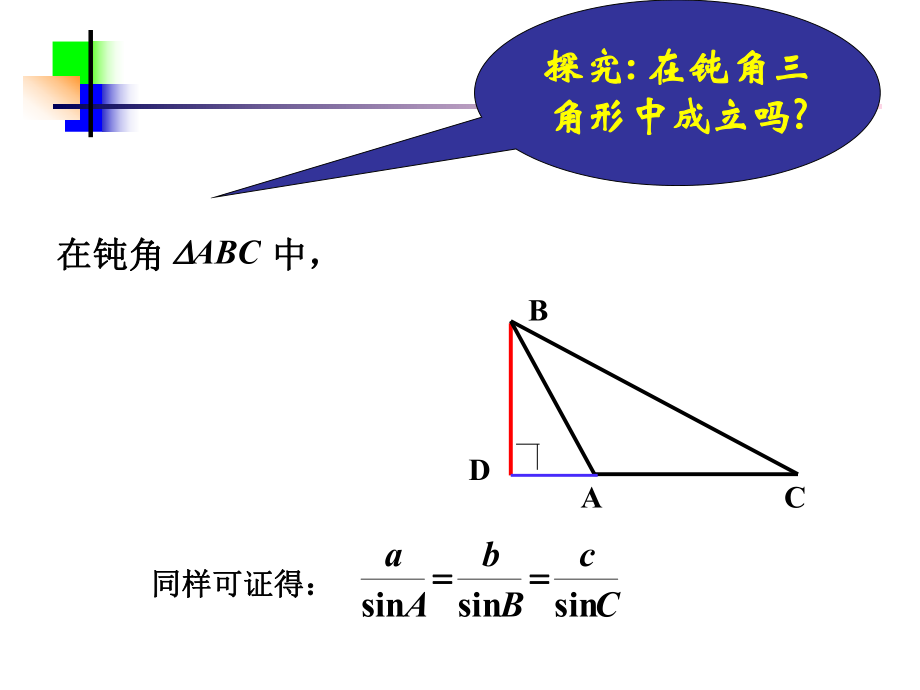
2、又：CcBbAasinsinsin ACB在钝角在钝角 中，中，ABC 同样可证得：同样可证得：CcBbAasinsinsin 探究探究: : 在钝角三在钝角三角形中成立吗角形中成立吗? ?D A c D O b B a CRCcBbAaRAaARDRaADRBDBDOB2sinsinsin2sinsin2sin2,2 同理：同理：即：即：，则，则设设，的直径的直径作圆作圆如图：过如图：过探究探究2:RCcBbAa2sinsinsin 正弦定理正弦定理 在一个三角形中，各边和它所在一个三角形中，各边和它所对角的正弦的比相等，即对角的正弦的比相等，即正弦定理可以解什么类型的三角形问题？正弦定理可

3、以解什么类型的三角形问题？ 1. 已知两角和任意一边，可以求出其他两边和一角；已知两角和任意一边，可以求出其他两边和一角；2.已知两边和其中一边的对角，可以求出三角形的其已知两边和其中一边的对角，可以求出三角形的其它的边和角它的边和角。正弦定理正弦定理例题讲解例题讲解 例例1 在在 中，已知中，已知 ，求求b（保留两个有效数字）（保留两个有效数字）. . ABC 30,45,10CAc解：解： 且且CcBbsinsin 105)(180CAB1930sin105sin10sinsin CBcb正弦定理正弦定理例例2 在在 中中,已知已知 ，求，求 。ABC 45, 24, 4BbaA例题讲解例

4、题讲解解：由解：由 BbAasinsin 得得 21sinsin bBaA 在在 中中 ABC ba A 为锐角为锐角 30A正弦定理正弦定理例题讲解例题讲解 例例3 在在 中，中， ，求，求 的面积的面积S ABC )13(2,60,45 aCBABC BacCabsin21sin21 Abcsin21 hABCaABCahS21 三角形面积公式三角形面积公式解：解： 75)(180CBA由正弦定理得由正弦定理得 4426)22)(13(2sinsin ABab326)23(4)13(221sin21 CabSABC 正弦定理正弦定理练习：练习：（1）在）在 中，一定成立的等式是（中，一定成

5、立的等式是（ ） ABC BbAaAsinsin. BbAaBcoscos. AbBaCsinsin. AbBaDcoscos. CABC （2）在）在 中，若中，若 ，则，则 是是( ) A等腰三角形等腰三角形 B等腰直角三角形等腰直角三角形 C直角三角形直角三角形 D等边三角形等边三角形2cos2cos2cosCcBbAa ABC D正弦定理正弦定理练习：练习：（3）在任一）在任一 中，求证：中，求证： ABC 0)sin(sin)sin(sin)sin(sin BAcACbCBa证明：由于正弦定理：令证明：由于正弦定理：令 CkcBkBAkasin,sin,sin 左边左边 代入左边得：代入左边