信号与系统第六章

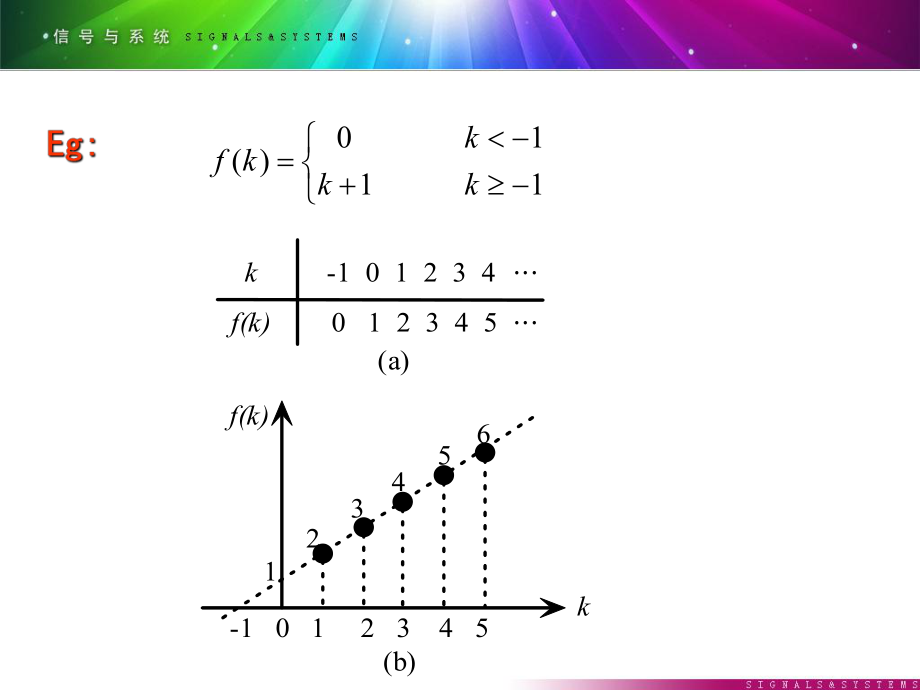
1、1、定义：如果信号仅在一些离散的瞬间具有确定的数值，则称之为离散时间信号。一般用f(kT)表示，其中k=0,1,2,；T为离散间隔。把这种按一定规则有秩序排列的一系列数值称为序列，简记为f(k)。常用序列f(k)表示。 也可以用数据表格形式给出，或以图形方式表。 1110)(kkkkf k -1 0 1 2 3 4f(k)0 1 2 3 4 5kf(k)123456-1 0 1 2 3 4 5(a)(b)图 7 - 1（1）相加 ：f(k)=f1(k)+f2(k) （2） 相乘 ： f(k)=f1(k)f2(k) （3）数乘 ：（4）累加和： （1）移位 m为大于零的整数。为大于零的整数。 k

2、f(k)1.50.5-1 0 1 2 3 4 50.51(a)ky(k)=f(k-2)1.50.5 1 2 3 4 5110.5-1 0(b)ky(k)=f(k+2)1.50.5-3 -2 -1 0 1 2110.5-5 -4(c)图 7 - 3（3）倒相 （4）展缩 需要注意的是需要注意的是，对f(k)进行展缩变换后所得序列y(k)可能会出现k为非整数情况，在此情况下舍去这些非整数的k及其值。 例6.1.1：若x(n)的波形如图所示，求x(2n) x(n/2)的波形。 还应指出，对于离散信号压缩后再展宽不能恢复原序列。（5）差分 （a）f(k)的后向差分，记 (b) f(k)的前向差分，记1

3、.单位序列k1(k)图 7 - 5-1 0 1)()0()()(kfkkf性质：)()()()(mkmfmkkf)()()()(mkmfmkkfk1U(k)图 7 - 6-1 0 1 2 3 4其他 010 1)(NkkGNk1GN(k)图 7 - 7-1 0 1 2 3N-1 N4.单边实指数序列 000)(kkakfk (a为实数) (7-13)k1f(k)=akU(k)|a|1-1 0 1 2 3 4 5k1f(k)=akU(k)|a|1-1 0 1 2 3 4 5(a)(b)图 7 - 85.正弦序列f(k)E k0 1 23 4 5图 7 - 9Eg:若离散信号f(k)满足 则f(k

4、)为周期离散时间信号，其重复周期T=N，重复角频率为 （1）齐次性、叠加性和线性 当系统 Taf(k)=aTf(k) 则称系统满足齐次性。 当系统则称系统满足叠加性 当系统同时满足齐次性和叠加性时，则称该系统满足线性 （2）线性离散时间系统 若离散时间系统的响应可分解为零输入响应和零状态响应(可分解性)； 且零输入响应和零状态响应分别满足齐次性和叠加性(零输入线性、零状态线性)，则称该系统为线性离散时间系统。 （3）时变与时不变离散时间系统 若 )()(kfTky例6.1.2 若已知k0时三个系统的响应分别为：(1) y(k)=kf(k)； (2) y(k)=|f(k)|；(3) y(k)=2

5、f(k)+3f(k-1)。试判断这三个系统各为哪类系统。 解解: : (1) 因激励与响应之间满足齐次性和叠加性，即但激励与响应之间不满足时不变性，即)()()(kykkfkfT )()()()(kaykfaTkakfkafT)()()()()()(212121kykykkfkkfkfkfT)()()()()(mkfmkmkymkkfmkfT故该系统为线性时变离散时间系统(2) 该系统激励与响应之间不满足齐次性，不满足叠加性。激励和响应之间满足时不变性，故此系统为非线性时不变系统。 )()()(kaykfTakafT)()()()()()()()(21212121kfkfkykykfkfkfk

6、fT)()()(mkfmkfTmky(3) 由给出的输入输出关系可知此系统是一个线性时不变离散时间系统。 解解 :设系统零输入响应为yx(k)，零状态响应为yf(k)，则根据线性时不变系统的特性，响应 )()()(kykykyfxkkfxkykfky)3(10)2(12)(2)(2)(例6.1.5：电阻梯形网络Ev0v1v2vNvN-1v0=E,vN=0,试写出节点电压的差分方程。试写出节点电压的差分方程。RRRRvN-2RRRR121) 1()()()() 1(RkukuRkuRkuku整理后可得： 0) 1()()2() 1(21kukuRRku或：0)2k(u)1k(u )RR2()k(

7、u21 (b) 加法器(a) 延时器五、 离散时间系统的模拟1、基本运算单元xn xn+ynynE1xnxn-1xnxn-1D D(c) 数乘器axn axnaxn axnaxn axn解解: : 根据系统差分方程，可得1017819176)(232EEEEEEH或 ：32132110178119176)(EEEEEEEH2、系统模拟1/E19f(k)图 7 - 181/E1/E-8-17-10176y(k)称之为齐次差分方程 )() 3(2)2()(kukykky(k)1/E1f(k)图 7 - 191/E1/E2-2241/E-1nknC(常数)特解形式特解形式自由项自由项B （常数）21

8、0121.kkkkCCnC nCnC nnCe()jnAeA为 复 数01CCnjne()ne为实数an(a不是特征根)nC210121()rrnrrCC nC nCnC naan(a是r重特征根)sin(cos)nn或12cossinCnCn2非齐次差分方程0,)2(31)2() 1(32)(kkykkk 对于线性时不变离散时间系统，若激励为单位序列(k)时，其系统的零状态响应h(k)称为单位序列响应。 一、迭代法：是一种递推法，一个不断迭代过程，称之为迭代法 0 0)()() 1()(0kkykfkyaky对于一阶系统)()(kkf)() 1()(0kkhakh0)(kh0k)()(khk

9、y令) 1()()(0khakkh)()()(0kUakhk二、等效初值法 当k0时，系统等效为一个零输入系统。求系统单位序列响应转化为求系统等效零输入响应。 例例6.3.1 6.3.1 某离散时间系统如图所示。求系统单位序列响应。1/Ef(k)图 7 - 201/E11/2y(k)解：解： 由图可得系统的差分方程为 )()2(21) 1()(kfkykyky)()(kkf)()2(21) 1()(kkhkhkh0)(kh0k由迭代法可知等效初始值为 当k1时，有0212对应的特征方程为KKCCkh2211)(单位序列响应的形式与零输入响应形式相同6.4 6.4 卷积和卷积和一、离散系统的时域

10、分解0)()()(iikifkfkf(k) 62 1 2 3 4 5 6 7442-1 0图 7 - 21)5(2)4(4)3(6)2(4) 1(2)(kkkkkkf1、交换律、结合律和分配律（1）交换律卷积和的性质：12122121 mmx nx nx m x nmx m x nmx nx n12122121 mmx nx nx m x nmx m x nmx nx n二、 卷积和 设两个离散时间信号为f1(k)和f2(k) ，定义f1(k)与f2(k)的卷积和运算为 （2）结合律 123123 x nx n x nx n x nx n（3）分配律 1231213 x nx nx nx n

11、x nx n x n2 2、移位性质、移位性质12112212 y nx nx nx n nx n ny n nn若则3、其它性质00 xnn nxn n xnnxn nmmxn unxmun mxm4、卷积和的计算： my nx m h nm（1）图解法反褶、平移、相乘、求和四个步骤：例例6.4.26.4.2 描述离散时间系统的差分方程为 已知y(-1)=1,求系统全响应y(k)。 )(05. 0) 1(9 . 0)(kUkyky解:(1) 求零输入响应yx(k)。 1) 1(0) 1(9 . 0)(xxxykykykxCky)9 . 0()(得C=0.9,故 1)9 . 0()(kxky(2) 求单位序列响应。 0 0)()(05. 0) 1(9 . 0)(kkhkkhkh利用等效初值法，可求得 )()9 . 0(05. 0)(kUkhk(3) 求激励时零状态响应。 )(