建筑力学,第六章内力及内力图,武汉理工

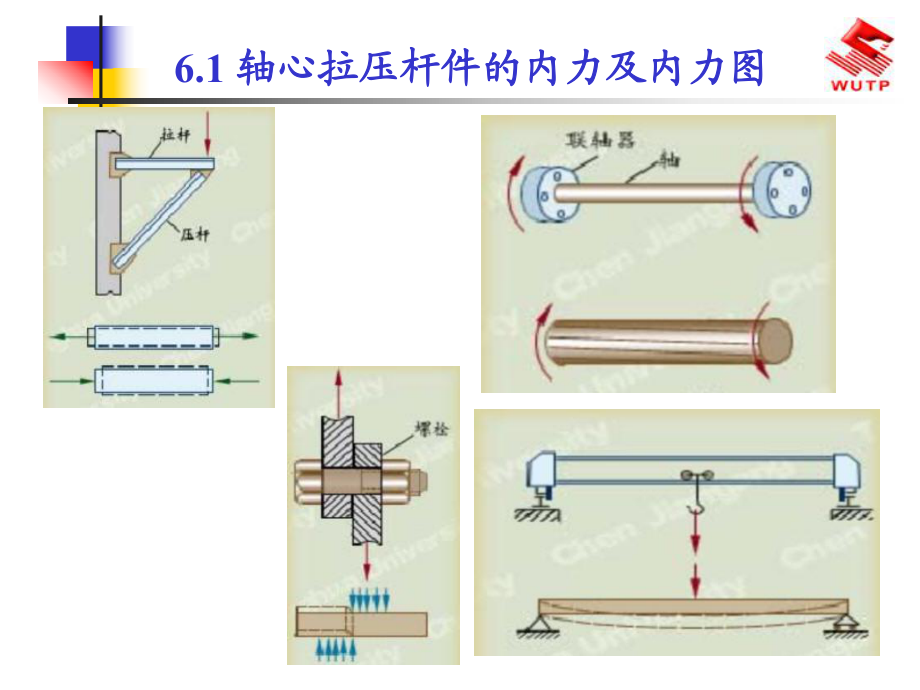
1、第六章内力及内力图第六章内力及内力图陈伟内力及内力图内力及内力图本章将先讨论三种基本变形构件的内力及内力图，本章将先讨论三种基本变形构件的内力及内力图，然后讨论其它各种结构和构件的内力及内力图，它们然后讨论其它各种结构和构件的内力及内力图，它们都是这三种基本变形的组合，包括多跨静定梁、斜梁、都是这三种基本变形的组合，包括多跨静定梁、斜梁、静定平面钢架、静定平面桁架、组合结构、静定拱等静定平面钢架、静定平面桁架、组合结构、静定拱等本章提要本章提要 6.1 轴心拉压杆件的内力及内力图轴心拉压杆件的内力及内力图 6.1 轴心拉压杆件的内力及内力图轴心拉压杆件的内力及内力图内力内力 ：在外力作用下构件

2、发生变形，构件内部相邻各质点间沿力作用方向的相对位置发生变化，同时构件各质点之间产生附加内力（简称内力），其作用是力图使各质点恢复其原始位置。 轴心抗压杆件受力特点：轴心抗压杆件受力特点：作用在杆件上的外力的作用线或外力合力的作用线与杆件轴线重合。轴心抗压杆件变形特点：轴心抗压杆件变形特点：杆件沿轴线方向伸长或缩短，同时横向尺寸也发生变化。 6.1 轴心拉压杆件的内力及内力图轴心拉压杆件的内力及内力图 6.1 轴心拉压杆件的内力及内力图轴心拉压杆件的内力及内力图 6.1 轴心拉压杆件的内力及内力图轴心拉压杆件的内力及内力图 6.1 轴心拉压杆件的内力及内力图轴心拉压杆件的内力及内力图 6.1

3、轴心拉压杆件的内力及内力图轴心拉压杆件的内力及内力图轴力：轴力：杆横截面上分布内力的合力沿杆轴线方向的分量称为轴力，用符号N表示。轴力轴力N的正负号规定：拉为正、压为负。 轴力方程：轴力方程：轴力N与杆横截面位置坐标x之间的函数关系表达式。轴力图：轴力图：用来表示轴力随截面位置不同而变化的情况的图形。lxxNPN图N+AlPP 6.1 轴心拉压杆件的内力及内力图轴心拉压杆件的内力及内力图求内力的方法求内力的方法 截面法截面法 ： 截面法是建筑力学研究内力的一个基本方法，其步骤如下：（1）截开：）截开： 在需求内力的截面处，将构件假想截分为两部分； （2）代替：）代替： 任取一部分为研究对象，弃

4、去另一部分，并以内力代替弃去部分对留下部分的作用； （3）平衡：）平衡： 对留下部分建立平衡方程，求出该截面的内力。 例例1 如图变截面圆钢管。已知如图变截面圆钢管。已知 F1=10kN，F2=35kN，F3=20kN。求各段横截面上的轴力，画轴力图。求各段横截面上的轴力，画轴力图。解解： 应用截面法在应用截面法在1-1、2-2、3-3截面截面处将杆截开，取右边部分，各截面轴处将杆截开，取右边部分，各截面轴力分别为力分别为N1、N2、N3都按正向规定设都按正向规定设为拉力。为拉力。11212312310(kN)25(kN)45(kN)NFNFFNFFF 扭转角（扭转角（ ）：任意两截面绕轴线转

5、动而发生的角位移）：任意两截面绕轴线转动而发生的角位移。ABOMeMeOBA受力特点：受力特点：杆件受到作用面垂直于杆轴线的力偶的作用。杆件受到作用面垂直于杆轴线的力偶的作用。变形特点变形特点：相邻横截面绕杆轴产生相对旋转变形。相邻横截面绕杆轴产生相对旋转变形。扭 转 6.2 扭转轴的内力及内力图扭转轴的内力及内力图扭 转框架结构边梁和雨篷梁框架结构边梁和雨篷梁 传递轴的传递功率、转速与外力偶矩的关系：传递轴的传递功率、转速与外力偶矩的关系：其中：其中： P 功率，千瓦（功率，千瓦（kW） n 转速，转转速，转/分（分（r/min）其中：其中：P 功率，马力功率，马力m)(N9549nPMem

6、)(N7024nPMe扭 转扭矩的符号规定扭矩的符号规定： T 的转向与截面外法线方向满足右手螺旋规则为正，的转向与截面外法线方向满足右手螺旋规则为正，反之为负。反之为负。 扭矩扭矩：构件受扭时，横截面上的内力偶矩，记作：构件受扭时，横截面上的内力偶矩，记作T T。 截面法求扭矩截面法求扭矩MeMeeexMTMTM 0 0MeTx扭 转 使卷曲右手的四指其转向与扭矩使卷曲右手的四指其转向与扭矩T T 的转向相同，若的转向相同，若大拇指的指向离开横截面，则扭矩为正；反之为负。大拇指的指向离开横截面，则扭矩为正；反之为负。MeTn扭 转xT扭 转 表示沿杆件轴线各横截面上扭矩变化规律的表示沿杆件轴

7、线各横截面上扭矩变化规律的图线。图线。扭 转 例例6-1 传动轴如图示，主动轮传动轴如图示，主动轮A输入功率输入功率PA=120kW，从动轮从动轮B、C、D输出功率分别为输出功率分别为PB=30kW，PC=40kW，PD=50kW，轴的转速，轴的转速n=300r/min。试作出该轴的扭矩图。试作出该轴的扭矩图。 解解 （1） 计算外力偶矩计算外力偶矩 m3.82kNm3819.6NmN30012095499549nPMAeAm0.95kN eBMm1.27kN eCMm1.59kN eDM扭 转T1T21122（2）计算扭矩）计算扭矩截面截面1-1：0 xM01eBMTm95kN. 01eBM

8、T截面截面2-2：02eAeBMMTm2.87kN2eBeAMMT0 xM扭 转33截面截面3-3：0 xM03eDMTm1.59kN3eDMT0.952.871.59m)kN(TT3mkN87. 2maxT3. 绘制扭矩图绘制扭矩图AC段为危险截面。段为危险截面。 6.3 平面弯曲梁的内力及内力图平面弯曲梁的内力及内力图受力特点：受力特点：杆件受有作用线垂直于杆轴的横向力或作用面与杆轴共面的外力偶作用。变形特点：变形特点：杆轴线由直线变为曲线；杆的横截面形心在垂直于杆轴的方向有位移（挠度）；杆的横截面绕某个轴发生转动（转角）。maxyACDFxAyFByFAByB吊车大梁吊车大梁房屋建筑中的

9、楼（屋）面梁、挑梁弯曲内力平面弯曲的概念平面弯曲的概念如果弯曲杆具有纵向对称面，杆件所受到的所有外力都在纵向对称面内，则杆件发生弯曲变形后轴线变成对称面内的平面曲线，这种弯曲称为平面弯曲。对平面弯曲杆件而言，过轴线且垂直于纵向对称面的平面称为弯曲杆的中性层。设想平面弯曲杆由许多纵向纤维组成，中性层把弯曲杆分成两部分，其中一部分上的纵向纤维受拉，另一部分上的纵向纤维受压。梁的内力梁的内力梁：水平放置的以弯曲变形为主要变形的杆件。梁式杆：以弯曲变形为主要变形的杆件。静定梁的三种基本形式FNFQ QMFAyFByFNFQM梁横截面上的内力一般有两项：剪力FQ和弯矩M，有时还有FN 剪力剪力FQ：杆横

10、截面上分布内力的合力沿垂直于杆轴方向的分量称为剪力，用符号FQ表示。弯矩弯矩M：杆横截面上的分布内力向截面形心简化所得主矩矢沿垂直于杆轴线方向的分量称为弯矩，用符号M表示。 剪力FQ和弯矩M的正负号规定简支梁简支梁外伸梁外伸梁悬臂梁悬臂梁FAxFAyFByFAxFAyFByFAxFAyMAFAyFNFSMFByFNFSM 截面上的剪力对梁上任意截面上的剪力对梁上任意一点的矩为一点的矩为顺时针顺时针转向时，转向时，剪剪力为正；力为正；反之反之为负。为负。 截面上的弯矩使得截面上的弯矩使得梁呈梁呈下凸形下凸形为为正；正；反之反之为负。为负。+_ 左顺右逆左顺右逆为正；为正；反之反之为负为负_+ 左

11、上右下左上右下为正；为正；反之反之为负为负梁的内力方程梁的内力方程FNFQ QMFAy求解梁横截面上内力的方法仍然是截面法。左图所示梁m-m截面的内力用截面法计算如下：0 xF0N F0yF1AQFFFy 0FMc)(1axFxFMAy剪力方程：剪力FQ与杆横截面位置坐标x之间的函数关系表达式。弯矩方程：弯矩M与杆横截面位置坐标x之间的函数关系表达式。梁的剪力方程和弯矩方程一般是分段函数。求梁剪力的简便方法：截面上的剪力等于截面任一侧的梁段上所有截面上的剪力等于截面任一侧的梁段上所有外力竖向分量的代数和。外力竖向分量的代数和。求梁弯矩的简便方法：截面上的弯矩等于截面任一侧的梁段上所有截面上的弯

12、矩等于截面任一侧的梁段上所有外力对截面形心之矩的代数和。外力对截面形心之矩的代数和。梁的内力图一般包括剪力图（FQ图）和弯矩图（M图）。剪力图（FQ图）：表示剪力随截面位置不同而变化情况的图形。弯矩图（M图） ：表示弯矩随截面位置不同而变化情况的图形。qxlqx xM xFQqlFQ图2/2qlM图例例6 图示简支梁C点受集中力作用，试写出剪力方程和弯矩方程，并画出剪力图和弯矩图。BAlFAYFBYx2x1CFab例例7 图示简支梁C点受集中力偶作用，试写出剪力和弯矩方程，并画出剪力图和弯矩图。例例8 简支梁受均布载荷作用，试写出剪力方程和弯矩方简支梁受均布载荷作用，试写出剪力方程和弯矩方程，

13、并画出剪力图和弯矩图。程，并画出剪力图和弯矩图。 弯矩、剪力、荷载集度间的微分关系弯矩、剪力、荷载集度间的微分关系M、FQ和和q间的微分关系在梁内力图中的几何意义间的微分关系在梁内力图中的几何意义M、FQ和和q间的微分关系在梁内力图中的几何意义间的微分关系在梁内力图中的几何意义(1)载荷集度、剪力和弯矩关系：载荷集度、剪力和弯矩关系：)()()(22xqdxxdFdxxMds1. q0，Fs=常数，常数， 剪力图为直线；剪力图为直线； M(x) 为为 x 的一次函数，弯矩图为斜直线。的一次函数，弯矩图为斜直线。2. q常数，常数，Fs(x) 为为 x 的一次函数，剪力图为斜直线；的一次函数，剪

14、力图为斜直线； M(x) 为为 x 的二次函数，弯矩图为抛物线。的二次函数，弯矩图为抛物线。 分布载荷向上（分布载荷向上（q 0），抛物线呈凸形；），抛物线呈凸形； 分布载荷向下（分布载荷向下（q 0），抛物线呈凹形。），抛物线呈凹形。 3. 剪力剪力Fs=0处，弯矩取极值。处，弯矩取极值。4. 集中力作用处，剪力图突变；集中力作用处，剪力图突变； 集中力偶作用处，弯矩图突变集中力偶作用处，弯矩图突变 M、FQ和和q间的微分关系在梁内力图中的几何意义间的微分关系在梁内力图中的几何意义(2)也可以通过积分方法确定剪力、也可以通过积分方法确定剪力、 弯矩图上各点处的数值弯矩图上各点处的数值利用微分

15、关系绘制梁的内力图利用微分关系绘制梁的内力图利用弯矩、剪力、荷载集度间的微分关系绘制梁内力图的方法如下：上述第三步和第四步可分段穿插进行。例例8 简支梁受力的大小和方向如图示，试画出其剪力图简支梁受力的大小和方向如图示，试画出其剪力图和弯矩图。和弯矩图。例例9 试画出梁的剪力图和弯矩图。试画出梁的剪力图和弯矩图。例例10 试画出图示有中间铰梁的剪力图和弯矩图。试画出图示有中间铰梁的剪力图和弯矩图。叠加原理与弯矩图叠加法叠加原理与弯矩图叠加法叠加原理：叠加原理：几个外力共同作用所引起的某一量值（支座反力、内力、变形等）等于每个外力单独作用所引起的该量量值的代数和。叠加原理的应用条件是小变形。叠加

16、原理的应用条件是小变形。弯矩图叠加的实质弯矩图叠加的实质弯矩图叠加的实质是弯矩竖标的代数叠加（而不是图形的弯矩图叠加的实质是弯矩竖标的代数叠加（而不是图形的简单叠加）。同侧相加，异侧相减。简单叠加）。同侧相加，异侧相减。直杆段弯矩图的区段叠加法直杆段弯矩图的区段叠加法直杆区段的弯矩图叠加可利用简支梁的弯矩图叠加法。其步骤直杆区段的弯矩图叠加可利用简支梁的弯矩图叠加法。其步骤是：是： （）计算直杆区段两端的最后弯矩值，以杆轴为基线画出这（）计算直杆区段两端的最后弯矩值，以杆轴为基线画出这两个值的竖标，并将两竖标连一直线；两个值的竖标，并将两竖标连一直线； （）将所连直线作为新的基线，叠加相应简支

17、梁在跨间荷载（）将所连直线作为新的基线，叠加相应简支梁在跨间荷载作用下的弯矩图作用下的弯矩图作梁内力图的简便方法作梁内力图的简便方法作内力图的最基本的方法是按内力函数作内力图。 作梁内力图的简便方法是求内力的简便方法和M、FQ、q之间 的微分关系以及区段叠加法的综合应用，其一般步骤为： 求出需要知道的支座反力； 选择控制截面将杆件分段；（接点处、分布荷载作用区段 的端点处是控制截面，划分出的区段内可包括一个集中力） 分段绘制内力图：先求出区段两个端点处的内力值，然后利 用M、FQ、q之间的微分关系和区段叠加法作出该区段的内力图。 例例11 作图示简支梁的内力图。作图示简支梁的内力图。例例12

18、求作图示伸臂梁的、图求作图示伸臂梁的、图例例12 续续例例13 比较图示斜梁和简支梁的异同比较图示斜梁和简支梁的异同多跨静定梁的内力分析多跨静定梁的内力分析多跨静定梁是由相互在端部铰接、水平放置的若干直杆件与大地通过支座连接而成的结构。多跨静定梁的组成及传力特征多跨静定梁的组成及传力特征多跨静定梁的组成及传力特征对图示梁进行几何组成分析：根据各杆之间的依赖、支承关系，引入以下两个概念： 基本部分：结构中不依赖于其它部分而独立与大地形成几何不变体的部分。 附属部分：结构中依赖基本部分的支承才能保持几何不变的部分。多跨静定梁的层叠图：用来形象的表现结构中各部分之间的依赖、支承关系的结构简图。 对多跨静定梁进行受力分析的顺序与进行几何组成分析的顺序刚好相反对多跨静定梁进行受力分析的顺序对多跨静定梁进行受力分析的顺序对多跨静定梁进行受力分析的顺序与进行几何组成分析的顺序刚好相反： 进行几何组成分析的顺序：先基本部分，后附属部分。进行受力分析的顺序：先附属部分，后基本部分。 多跨静定梁的内力计算多跨静定梁的内力计算例例14 计算图示多跨静定梁，并作内力图计算图示多跨静定梁，并作内力图例例14 续续例例15 求作图示多跨静定梁的FQ、M图例例15 续续桁