机械工程控制基础第六章

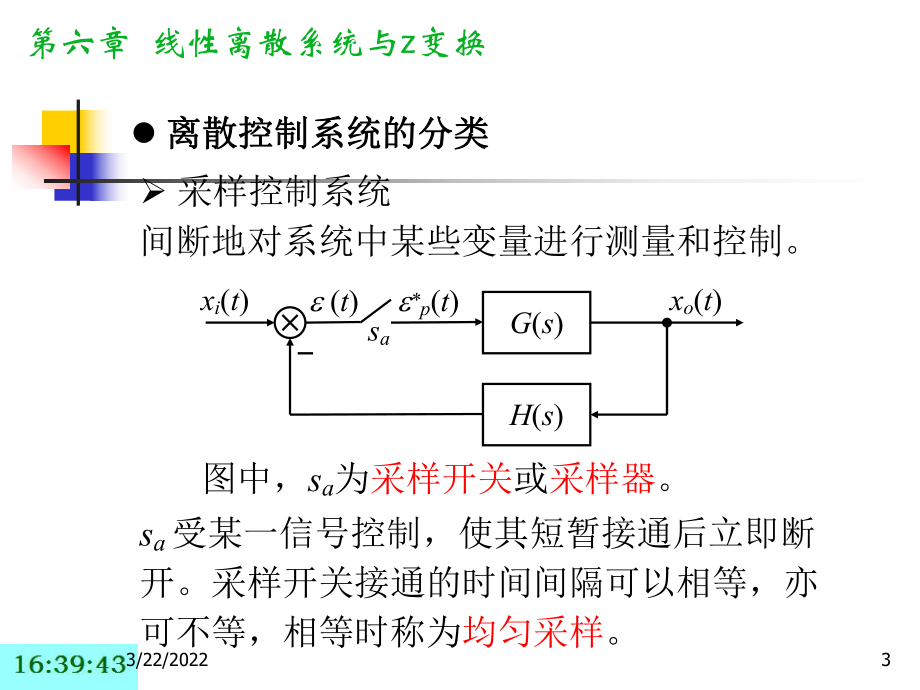
1、3/22/20221第六章 线性离散系统与z z变换二、采样过程与采样定理三、Z变换与Z反变换四、脉冲传递函数五、离散系统的稳定性分析六、数字控制器与离散PID控制一一、概述七、小结3/22/20222第六章 线性离散系统与z变换一一、概述l 连续系统与离散系统连续系统与离散系统 连续控制系统系统中各部分传递的信号为随时间连续变化的信号。连续控制系统通常采用微分方程描述。 离散控制系统系统中某一处或多处的信号为脉冲序列或数字量传递的系统。离散控制系统通常采用差分方程描述。 3/22/20223第六章 线性离散系统与z变换l 离散控制系统的分类离散控制系统的分类 采样控制系统间断地对系统中某些变

2、量进行测量和控制。sa 受某一信号控制，使其短暂接通后立即断开。采样开关接通的时间间隔可以相等，亦可不等，相等时称为均匀采样。图中，sa为采样开关或采样器。G(s)H(s)xi(t)xo(t)sa (t)*p(t)3/22/20224第六章 线性离散系统与z变换连续信号 (t)经采样开关后成为离散信号*p(t)。该过程称为采样，相应离散控制系统称为采样控制系统。t (t)0t0*p(t)采样控制系统的特点：采样开关闭合时，系统处于闭环工作状态，断开时处于开环状态。3/22/20225第六章 线性离散系统与z变换采样控制最早出现于某些大惯性或具有较大滞后特性的对象控制中。例如，工业炉温度控制系统

3、。工业炉可以视为具有延迟时间 的惯性环节，其延迟时间可长达数秒甚至数十秒，惯性时间常数也相当大，采用常规控制无法解决控制精度与动态性能之间的矛盾，而采用采样控制将取得良好的控制效果：可以取较大的开环增益保证稳态精度，又可抑制系统调节过头产生大幅振荡。3/22/20226第六章 线性离散系统与z变换 数字控制系统系统中含有数字计算机或数字编码元件。图中，A/D：模拟信号至数字信号转换器； D/A：数字信号至模拟信号转换器。被控对象H(s)xi(t)xo(t) (t)*(t)A/D计算机D/A3/22/20227第六章 线性离散系统与z变换q A/D转换采样x(t)模拟信号取样信号s(t)0ts(

4、t)xs(t)量化编码数字信号x(n)0tx(t)0tx(nt)tt0qx(n)000001010011nx(nt)3/22/20228第六章 线性离散系统与z变换 D/A转换D/A转换器低通滤波器nx(n)tx(t)tx(t)x(n)x(t)x(t)3/22/20229第六章 线性离散系统与z变换被控对象H(s)xi(t)xo(t) (t)*(t)计算机保持器sam*(t)sbm(t)图中，sa 与sb同步开关。 保持器：实现信号复现。将离散信号恢 复为模拟信号。3/22/202210第六章 线性离散系统与z变换t (t)0t0*(t)t0m*(t)t0m(t)3/22/202211第六章

5、线性离散系统与z变换l 离散控制系统的特点离散控制系统的特点 采样信号特别是数字信号可以有效抑制噪声， 从而提高系统抗干扰能力； 由计算机构成的数字控制器，控制规律由软 件实现，易于改变，控制灵活，且效果优于 连续式控制。 允许采用高灵敏度控制元件，提高控制精度。 可实现分时控制若干系统，提高设备利用率。 对大延迟系统可以引入采样方式稳定。 可以实现各种先进控制方式。3/22/202212第六章 线性离散系统与z变换l 离散控制系统的研究方法离散控制系统的研究方法 差分方程 z变换经过 z 变换处理后的离散系统，可以将连续系统的分析方法经过适当改变应用于离散系统的分析和设计。 状态空间虽然采样

6、控制系统和数字控制系统的构成及部件存在基本区别，但其分析和设计方法相同。3/22/202213第六章 线性离散系统与z变换二、采样过程与采样定理l 采样过程采样过程sax(t)x*p(t)t0 x(t)t0t0T 2T 3T 4Tx*p(t)x*(t)设 sa 每隔时间T接通一次，接通时间为 ，并满足T 。 T 称为采样周期。其倒数称为采样频率。由于T ，故可近似认为在 时间间隔内，输出维持不变。3/22/202214第六章 线性离散系统与z变换从而：)2( 1)2( 1)2( )( 1)( 1)()( 1)( 1)0()(*TtTtTxTtTtTxttxtxp0)( 1)( 1)(nnTtn

7、TtnTx0)( 1)( 1 )(nnTtnTtnTx当 T，且远远小于离散系统连续部分的时间常数时，可近似认为 0。从而有：3/22/202215第六章 线性离散系统与z变换00*)( 1)( 1 )(lim)(npnTtnTtnTxtx)( 1)( 1lim0nTtnTt1)( 1)( 1dtnTtnTt注意到：00*)()( )()()(nnpnTtnTxnTtnTxtx从而：3/22/202216第六章 线性离散系统与z变换0)()(nTnTtt)()()()()()()(00*ttxnTttxnTtnTxtxTnn令：sax(t)x*p(t)x*(t)可见，采样过程可理解为脉冲调制过

8、程，即连续输入信号 x(t) 对周期的理想脉冲载波信号进行调制，调制后在nT 时刻的脉冲强度为x(nT)。)()(*txtxp注意到：因此，采样开关结构图可表示为：3/22/202217第六章 线性离散系统与z变换显然由 X*(s)可以直接看出x*(t)的时间响应。但须注意，由于 x*(t) 只描述了 x(t) 在采样瞬时的数值，故 X* (s)不能给出 x(t)在采样间隔之间的信息。此外也不能认为x*(t) 在采样间隔内数值为0。上述分析过程中，假设了：x(t)=0，t 0，该条件对实际控制系统通常都是满足的。0*)()()(nnTsenTxtxLsX对x*(t) = x(t)T(t)进行拉

9、氏变换：3/22/202218第六章 线性离散系统与z变换l 采样定理采样定理x*(t)只给出了x(t)在时域的部分信息，为了能从x*(t)不失真地恢复出原始的连续信号x(t)，采样间隔（采样频率）需要满足一定的条件。时域采样原始信号f = f0fs=8f0fs=4f0fs=2f03/22/202219第六章 线性离散系统与z变换由上述时域采样图形分析可见： 对单个连续正弦信号进行采样，采样频率不 能低于信号频率的两倍； 对多个正弦信号叠加组成的信号进行采样， 采样频率不能低于信号中最高频率的两倍。sin2f0tsin14f0tsin2f0t+sin14f0t时域采样：混叠fs= 8f03/2

10、2/202220第六章 线性离散系统与z变换工程中的连续信号 x(t) 都可以通过傅立叶级数或傅立叶变换展开为多个或无穷个正弦信号分量的叠加，即信号的频域描述(频谱)。如对周期为T0的信号x(t)，其傅立叶级数展开1000sincos)(nnntnbtnaatx为信号角频率。002Tn为正整数。 其中：3/22/202221第六章 线性离散系统与z变换2/2/0000)(1TTdttxTa2/2/0000cos)(2TTndttntxTa2/2/0000sin)(2TTndttntxTb如非周期信号x(t)，其傅立叶变换对为dfefXtxdtetxfXftjftj22)()()()(3/22/

11、202222第六章 线性离散系统与z变换根据前述时域采样的分析，若连续信号 x(t) 不包含任何大于 max 的频率分量(带限信号)，则为了能从采样信号x*(t)无失真地恢复出原始的连续信号x(t) ，采样频率s必须满足： s 2max（或：fs 2fmax）此即为香农采样定理。实际采样时，fs常取为信号最高频率的34倍。 3/22/202223第六章 线性离散系统与z变换l 信号恢复信号恢复x(t)t0X()0max-maxAT(t)t0T 2T 3T4T5T 6T|T()|0s-sx*(t)t0T 2T3T4T5T 6T|X*()|0s-sA/T)()()(*ttxtxT)()()(*TX

12、X3/22/202224第六章 线性离散系统与z变换由图可见，采样信号x*(t)的频谱X*()是以采样角频率 s 为周期的无穷多个原连续信号x(t) 的频谱 X() 幅值变化了1/T 倍，并沿频率轴平移了ns后的和。n = 0处的频谱称为采样信号频谱的主分量， ns (n 0) 处的频谱为采样引起的高频辅助分量。易见，若采样信号x*(t) 满足采样定理，则通过截止频率为s/2的理想低通滤波器可准确地恢复出原始信号x(t) 的频谱 X()，即恢复出x(t)。3/22/202225第六章 线性离散系统与z变换实际滤波器不可能具有理想的频率截止特性，即理想滤波器是不存在的。工程中通常通过保持器（低通

13、滤波器）来恢复连续信号x(t)。 保持器数学描述从采样过程可知，在采样时刻上，脉冲序列的脉冲强度等于连续信号的幅值，但在两个相邻的采样时刻之间，连续信号的幅值未知，只能根据采样时刻的脉冲强度进行插值或外推。3/22/202226第六章 线性离散系统与z变换保持器就是实现外推功能的一种装置。能够物理实现的保持器只能根据现在时刻和过去时刻的采样值完成外推，而不能根据将来时刻的采样值完成外推。保持器的外推规律通常用多项式关系描述：mmtatataatnTx)()()(2210其中，0tT。系数 a0am 由过去m+1个采样值x*(n-m)T x*(nT)确定。 m称为保持器的阶次。3/22/2022

14、27第六章 线性离散系统与z变换 零阶保持器零阶保持器的外推公式为：TtnTxnTxatnTx0),()()(*0即零阶保持器按常值外推，将前一采样时刻nT 的采样值 x*(nT)一直保持到下一采样时刻(n+1)T 到来之前，从而使离散采样信号 x*(t)变成阶梯连续信号xh(t)。3/22/202228第六章 线性离散系统与z变换txh(t) x(t)0T2T 3T4T5T 6T 7Tx(t)xh(t)若将上述阶梯信号xh(t)的中点连接起来，即可得到与连续信号 x(t)形状一致但滞后半个采样周期的响应x(t -T/2)。注意到：0) 1(1)( 1)()(nhTntnTtnTxtx3/22

15、/202229第六章 线性离散系统与z变换若考虑保持器串接于采样器之后，并考虑保持器的输入为x*(t)，即将采样器中的考虑到保持器中去：00)1()(1 )()()(nnTsTsnTsnnTshhenTxseseenTxtxLsXsax(t)x*p(t)x*(t)零阶保持器xh(t)3/22/202230第六章 线性离散系统与z变换从而由：0*)()(nnTsenTxsX0*)()()(nnTtnTxtx可得结合后零阶保持器的传递函数：sesGTsh1)(因此，分析采样控制系统时，若保持器的传递函数表示为上述形式，则采样信号将直接表示为x*(t)，而不必考虑 的影响。3/22/202231第六

16、章 线性离散系统与z变换T0-22/T4/T6/T|Gh(j)|Gh(j)零阶保持器的频率特性：2/2/2/2/2/)2/sin( 1)(TjTjTjTjTjheTTTjeeejejG3/22/202232第六章 线性离散系统与z变换零阶保持器的特点：q 非理想的低通滤波器。允许部分高频分量 通过，导致恢复出的连续信号存在纹波。q 时间延迟特性。延迟时间为 T/2 ，使系统 相角滞后加大，对稳定性不利。相位滞后是各阶保持器的共性，与一阶及高阶保持器相比，零阶保持器具有最小的相位滞后，且结构简单，易于实现，因此，实际系统普遍采用零阶保持器。3/22/202233第六章 线性离散系统与z变换l Z

17、变换变换三、Z变换与Z反变换考虑连续信号x(t) (x(t)=0，t0)的z变换。解解：111 1)(112210zeezzzezezezetxZaTaTaTaTaTnnanT根据定义求得的z变换为无穷级数形式，对于常用函数z变换的级数形式，都可以写出其闭合形式。3/22/202238第六章 线性离散系统与z变换z变换的无穷级数形式具有明显的物理意义：z-n (n = 0, 1, 2, )的系数直接表示连续时间函数在各采样时刻上的采样值，而指数n表示从t = 0开始，以采样周期T为间隔的各个采样时刻nT。因此，z变换含有时间的概念，可由连续函数z变换的无穷级数形式清楚地看出其在各采样时刻上的采

18、样序列的分布情况。3/22/202239第六章 线性离散系统与z变换q 部分分式法步骤： 求已知连续时间函数x(t)的拉氏变换X(s)； 将X(s) 展开为部分分式形式，使每一部分 分式对应简单的时间函数，求得其相应的 z 变换；将各部分的z 变换相加获得x(t)的z变换。3/22/202240第六章 线性离散系统与z变换例4 已知连续函数的拉氏变换： 求相应的z变换。)()(assasXaTaTaTaTatezezezezzzzeZtZtxZzX)1 ()1 ( 1)( 1 )()(2解解：assassasX11)()(atetx1)(3/22/202241第六章 线性离散系统与z变换例5

19、求 x(t) = sint 的z变换。解解：jsjsjssX1121)(22jsjsjZzX1121)(TjTjezzezzj211cos2sin1)()(2122TzzTzeezzeezjTjTjTjTj3/22/202242第六章 线性离散系统与z变换q 留数计算法nrpssMsXiiirii)()()(若已知：ipssTrirriipssTiiiiiezzsXpsdsdrezzsXreszX)()()!1(1 )()(11则：3/22/202243第六章 线性离散系统与z变换例6 求单位速度函数x(t) = t (t 0)的z变换。解解：21)(ssXp1 = 0，r1 = 2nipss

20、TrirriiiiiezzsXpsdsdrzX111)()()!1(1)(0221)!12(1ssTezzssdsd202) 1()(zTzezTzessTsT3/22/202244第六章 线性离散系统与z变换q 其它方法例7 求 x(t) = cost 的z变换。解解：tjtjeet21cosTjTjtjtjezzezzeZeZzX2121)(1cos2)cos(2TzzTzz3/22/202245第六章 线性离散系统与z变换例8 求单位阶跃函数的z变换。解解：由于)0(lim)( 10tetata1lim lim)( 100zzezzeZtZaTaata3/22/202246第六章 线性离

21、散系统与z变换 z变换的性质q 线性性 Zax1(t)+bx2(t) = aZx1(t)+bZx2(t) 其中a、b为常数。q 时域位移定理)()(zXzkTtxZk10)()()(knnkznTxzXzkTtxZ其中k为正整数。滞后定理超前定理3/22/202247第六章 线性离散系统与z变换nnzkTnTxkTtxZ0)()(证明证明：)(0)(knnkzTknxzknmzmTxzmkmk)()(zXzk当m0时，x(mT)=0mmkzmTxz0)(3/22/202248第六章 线性离散系统与z变换nnzkTnTxkTtxZ0)()()(0)(knnkzTknxzknmzmTxzmkmk)

22、(mkmmmkzmTxzmTxz100)()(10)()(knnkznTxzXz3/22/202249第六章 线性离散系统与z变换q 复域位移定理)()(zeXtxeZaTatq 初值定理00)()(lim)0(tiftxzXxzq 终值定理)() 1(lim)(lim)(1zXznTxxzn若x(nT) (n = 0, 1, 2, ) 均为有限值，则：x(nT) (n = 0, 1, 2, ) 均为有限值也可表述为：(z-1)X(z)的全部极点位于z平面的单位圆内。3/22/202250第六章 线性离散系统与z变换证明证明：0)() 1()()(nnznTxTnxtxTtxZ)0()() 1

23、()()(zxzXztxTtxZ又由时域位移定理：即：0)() 1()0()() 1(nnznTxTnxzxzXz因此：00111)() 1()() 1(lim)0()() 1(lim)0()() 1(limnnnzzznTxTnxznTxTnxxzXzzxzXz3/22/202251第六章 线性离散系统与z变换NnNnnTxTnxnTxTnx00)() 1(lim)() 1(注意到：所以：存在若)(lim)() 1(lim)(lim)(1txzXztxxtzt)0()(lim)0() 1(limxtxxTNxtN3/22/202252第六章 线性离散系统与z变换q 卷积定理x(nT)与y(n

24、T)离散卷积定义为：00)()( )()()()(kkkTyTknxTknykTxnTynTx则：)()()()(zYzXnTynTxZ3/22/202253第六章 线性离散系统与z变换证明证明：00)()()()(nnkkznTyzYzkTxzX000)()( )()()()(knnkkzTknykTxzYzkTxzYzX时域位移定理00)()(nnkzTknykTx)()()()(0nTynTxZznTynTxnn3/22/202254第六章 线性离散系统与z变换l Z反反变换变换x(nT) = Z-1X(z)Z反变换的信号序列仍是单边的，即当n0后，该极点消失。5 . 0)2)(1(1)

25、(001zznzzzzzXres当n=0时：3/22/202266第六章 线性离散系统与z变换322) 1( )() 1()(111111znznznzzzzzXzzzXresnznznznzzzzzXzzzXres)2(311) 1( )()2()(2121213/22/202267第六章 线性离散系统与z变换所以：6131325 . 0)0(x, 3, 2, 1)2(3132)(nnTxn01*)()2(3132)(5 . 0 )()2(3132)(61)(nnnnnTttnTtttx3/22/202268第六章 线性离散系统与z变换 Z变换及反变换只反映X(z)与x*(t)间的关系；l

26、关于Z变换与反变换的说明对于连续时间函数而言，Z变换及Z 反变换都不是唯一的。 为了全面描述 Z 反变换后x*(t)的函数特性， 可以令采样周期T0。3/22/202269第六章 线性离散系统与z变换l 采样系统的数学模型差分方程 微分与差分tx(t)0t t+dtdx(t)nx(n)0n-1 n n+1x(n)x(n)微分：dx(t) = x (t)dt一阶前向差分：x(n) = x(n+1) - x(n)一阶后向差分：x(n) = x(n) - x(n-1)省略采样周期T3/22/202270第六章 线性离散系统与z变换 高阶差分二阶前向差分： 2x(n) = x(n) = x(n+1)

27、- x(n) = x(n+2) - 2x(n+1) + x(n)二阶后向差分： 2x(n) = x(n) = x(n) - x(n-1) = x(n) - 2x(n-1) + x(n-2)k阶前向差分： kx(n) = k-1x(n+1) - k-1x(n)k阶后向差分： kx(n) = k-1x(n) - k-1x(n-1)3/22/202271第六章 线性离散系统与z变换q 前向差分 差分的Z变换Zx(n) = Zx(n+1) - x(n) = (z - 1)X(z) - zx(0)Z2x(n) = (z - 1)2X(z) - z(z - 1)x(0) - zx(0)101)0() 1(

28、)() 1()(nrrrnkkxzzzXznxZ)0()0(0 xx其中：Z变换中因子(z - 1)与拉氏变换中s的作用相同。3/22/202272第六章 线性离散系统与z变换q 后向差分0 0)()(1)(tiftxzXzznxZ0 0)()(1)(22tiftxzXzznxZ0 0)()(1)(tiftxzXzznxZkk3/22/202273第六章 线性离散系统与z变换l 采样系统的数学模型差分方程 微分与差分tx(t)0t t+dtdx(t)nx(n)0n-1 n n+1x(n)x(n)微分：dx(t) = x (t)dt一阶前向差分：x(n) = x(n+1) - x(n)一阶后向差

29、分：x(n) = x(n) - x(n-1)省略采样周期T3/22/202274第六章 线性离散系统与z变换 高阶差分二阶前向差分： 2x(n) = x(n) = x(n+1) - x(n) = x(n+2) - 2x(n+1) + x(n)二阶后向差分： 2x(n) = x(n) = x(n) - x(n-1) = x(n) - 2x(n-1) + x(n-2)k阶前向差分： kx(n) = k-1x(n+1) - k-1x(n)k阶后向差分： kx(n) = k-1x(n) - k-1x(n-1)3/22/202275第六章 线性离散系统与z变换q 前向差分 差分的Z变换Zx(n) = Z

30、x(n+1) - x(n) = (z - 1)X(z) - zx(0)Z2x(n) = (z - 1)2X(z) - z(z - 1)x(0) - zx(0)101)0() 1()() 1()(nrrrnkkxzzzXznxZ)0()0(0 xx其中：Z变换中因子(z - 1)与拉氏变换中s的作用相同。3/22/202276第六章 线性离散系统与z变换q 后向差分0 0)()(1)(tiftxzXzznxZ0 0)()(1)(22tiftxzXzznxZ0 0)()(1)(tiftxzXzznxZkk3/22/202277第六章 线性离散系统与z变换 差分方程)()()(txtydttdy例：

31、微分方程的离散化dtTTnTyTnydtndtydtndtydttydttydttdy)() 1( )()()()()()()()() 1(nTxnTyTnTyTny)()(1) 1(nTxTnTyTTny差分方程)()() 1(00nxbnyany3/22/202278第六章 线性离散系统与z变换一般，n阶离散系统的前向差分方程为：)() 1() 1()()() 1() 1()(11011kxbkxbmkxbmkxbkyakyankyankymmnn初始条件为：y(i) = yi (i = 0 n-1) x(i) = xi (i = 0 m-1)n阶离散系统的后向差分方程为：)() 1()

32、1()()() 1() 1()(11011mkxbmkxbkxbkxbnkyankyakyakymmnn初始条件为： y(k) = x(k) = 0 (k0)。3/22/202279第六章 线性离散系统与z变换 差分方程的求解q 迭代法根据给定的初值，利用差分方程的递推关系，迭代求出输出序列。例1 已知差分方程 y(k) 5y(k-1) + 6y(k-2) = x(k)输入序列x(k)1，初始条件为y(k) = 0 ( k 0)，求输出y(k) (k05)。3/22/202280第六章 线性离散系统与z变换解解：y(k) x(k) + 5y(k-1) - 6y(k-2)y(0) x(0) +

33、5y(-1) - 6y(-2) = 1y(1) x(1) + 5y(0) - 6y(-1) = 6y(2) x(2) + 5y(1) - 6y(0) = 25y(3) x(3) + 5y(2) - 6y(1) = 90y(4) x(4) + 5y(3) - 6y(2) = 301y(5) x(5) + 5y(4) - 6y(3) = 9663/22/202281第六章 线性离散系统与z变换q Z变换法对差分方程两端取Z变换，利用时域位移定理，得到关于z 的代数方程，求得Y(z)后，通过Z反变换得到输出序列y(k)。例2 已知差分方程 y(k) 5y(k-1) + 6y(k-2) = x(k)输

34、入序列x(k)1，初始条件为y(k) = 0 ( k 0)，求输出y(k) 。3/22/202282第六章 线性离散系统与z变换解解：对方程两端进行Z变换：Zy(k) 5y(k-1) + 6y(k-2) = Zx(k)Y(z) 5z-1Y(z) + 6z-2Y(z) = X(z)(6511)(21zXzzzY)3)(2)(1(165322zzzzzzzzz35 . 42415 . 0zzzzzz. 2, 1, 0,)3(5 . 4)2(45 . 0)(kkykk3/22/202283第六章 线性离散系统与z变换例3 已知差分方程 y(k+2) 5y(k +1) + 6y(k) = 0初始条件为

35、y(0) = 0，y(1) = 1，求输出y(k)。解解：对方程两端进行Z变换：Zy(k+2) 5y(k +1) + 6y(k) = 00)(6)0(5)(5) 1 ()0()(22zYzyzzYzyyzzYzzzyyyzzYzz)0(5) 1 ()0()()65(223265)(2zzzzzzzzY, 2, 1, 0,32)(kkykk3/22/202284第六章 线性离散系统与z变换四、脉冲传递函数l 脉冲传递函数的定义G(s)xi(t)xi*(t)xo(t)xo*(t)s1s2G(z)s1和s2为同步采样器。脉冲传递函数：零初始条件下，输出采样信号xo*(t)的z变换与输入采样信号xi*

36、(t)的z变换之比。记为：00)()()()()(kkikkoiozkTxzkTxzXzXzG3/22/202285第六章 线性离散系统与z变换零初始条件：xo(t) = xi(t) = 0 (t0) 或：xo(kT) = xi(kT) = 0 (k0)实际系统的输出往往是连续信号，即采样开关s2不存在，此时，可以在输出端虚设一采样开关，并使其与输入采样开关s1同步，以考察连续输出在各采样时刻的状态。G(s)xi(t)xi*(t)xo(t)xo*(t)s1s2G(z)3/22/202286第六章 线性离散系统与z变换l 脉冲传递函数的意义前述已知，对线性连续系统，输出y(t)与输入x(t)之间

37、满足：ttdtgxdtxgtxtgty00)()()()()()()(式中，当t 0时，g(t) = x(t) = 0。 g(t)L-1G(s)为系统的脉冲响应函数。3/22/202287第六章 线性离散系统与z变换对图示采样系统，直接作用于系统连续部分的信号为：G(s)xi(t)xi*(t)xo(t)xo*(t)s1s2G(z)0*)()()(niinTtnTxtx从而：)()()(*txtgtxio3/22/202288第六章 线性离散系统与z变换因此，输出量在采样时刻的值为：tniodnTnTxtgtx00)()()()(即：00)()()(ntidnTtgnTx0)()(ninTtgn

38、TxkninioTnkgnTxnTkTgnTxkTx00)()()()()()()(kTgkTxig(t)=0, if t03/22/202289第六章 线性离散系统与z变换即脉冲传递函数为系统单位脉冲响应序列g(kT)的z变换。通常简记为：从而：)()()(zGzXzXio0)()()()()(kkiozkTgkTgzzXzXzGG(z) = Zg(t) = ZL-1G(s) = ZG(s)需注意：zssGzG)()(zTssGzGln1)()(3/22/202290第六章 线性离散系统与z变换)() 1() 1()()() 1() 1()(11011mkxbmkxbkxbkxbnkxank

39、xakxakximimiiononoo若系统差分方程为：则当y(k)=x(k)=0 (k0)时，两端进行z变换可得：knioTnkgnTxkTx0)()()(由于：即xo(kT)为不同时刻的输入脉冲通过g(k-n)T加权后的和，因此，g(kT)通常称为加权序列。niininmjjnjniiimjjjiozazzbzazbzXzXzG10101)()()(3/22/202291第六章 线性离散系统与z变换若系统差分方程为：niininmjjmjiozazzbzXzXzG10)()()()() 1() 1()()() 1() 1()(11011kxbkxbmkxbmkxbkxakxankxankx

40、imimiiononoo当y(0) = y(1) = = y(n-1) = 0， x(0) = x(1) = = x(m-1) = 0时，两端进行z变换可得：3/22/202292第六章 线性离散系统与z变换l 环节串联时的脉冲传递函数离散系统中环节相互串联时，由于采样开关的位置和数目不同，求得的等效脉冲传递函数也不相同。 串联环节之间有采样器G1(s)x1(t)x1*(t)xo(t)xo*(t)s1s3G(z)G2(s)s2x2(t)x2*(t)s1、s2、s3为同步采样器。3/22/202293第六章 线性离散系统与z变换)()()()(1121sGZzXzXzG)()()()(222sG

41、ZzXzXzGo因此：)()()()()()()()()(212121zGzGzXzXzXzXzXzXzGoo即当两环节之间存在采样开关时，等效脉冲传递函数等于两环节脉冲传递函数的乘积。同理： n 个环节相串联时，若相邻环节间均存在同步采样器，则等效脉冲传递函数等于 n 个环节脉冲传递函数的乘积。3/22/202294第六章 线性离散系统与z变换 串联环节之间无采样器G1(s)xi(t)xi*(t)xo(t)xo*(t)s1s2G(z)G2(s)s1、s2为同步采样器。)()()()()()(2121zGGsGsGZzXzXzGio与G1(z)G2(z)相区别即当两环节之间无采样开关时，等效脉

42、冲传递函数等于两环节传递函数相乘后相应的脉冲响应函数的z变换。3/22/202295第六章 线性离散系统与z变换G1(s)x1(t)x1*(t)xo(t)xo*(t)s1s3G(z)G2(s)s2x2(t)x2*(t)s1、s2、s3为同步采样器。例1 已知采样系统方框图如下：其中：1101)(1ssG151)(2ssG比较有s2与无s2时，系统的脉冲传递函数。3/22/202296第六章 线性离散系统与z变换解解：1）有s2时)()()()()(2121sGZsGZzGzGzG1511101sZsZTTezzezz2 . 01 . 02 . 01 . 0)(02. 02 . 01 . 02T

43、Tezezz3/22/202297第六章 线性离散系统与z变换2）无s2时)()()()(2121sGsGZzGGzG1511101ssZTTezzezz2 . 01 . 02 . 0)()(2 . 02 . 01 . 02 . 01 . 0TTTTezezeez显然，G1(z)G2(z) G1G2(z)。尽管如此，易见采样开关只影响脉冲传递函数的零点。3/22/202298第六章 线性离散系统与z变换例2 已知采样系统方框图如下：其中：sesGsTh1)()()(1assasG求系统的脉冲传递函数。Gh(s)xi(t)xi*(t)xo(t)xo*(t)s1s2G(z)G1(s)s1、s2为同

44、步采样器。3/22/202299第六章 线性离散系统与z变换解解：此系统为有零阶保持器的系统。)()()()(11sGsGZzGGzGhh )(11sGseZsTssGessGZsT)()(11ssGeZssGZsT)()(11由于e-sT为延迟一个采样周期的延迟环节，因此，e-sTG1(s)/s对应的时域输出比 G1(s)/s 对应的时域输出延迟了一个采样周期。3/22/2022100第六章 线性离散系统与z变换)(121assaZzasasasZz11111121aTezzazzazTzz111) 1(121)() 1()1 (1) 1(2aTaTaTezzaeaTzaTessGZzzG)

45、(1)(11根据z变换的时域滞后定理，有：3/22/2022101第六章 线性离散系统与z变换l 闭环系统的脉冲传递函数由于采样器位置可变，因此闭环离散系统没有唯一的结构图形式。考虑常见的偏差采样闭环离散系统：(t)*(t)xo(t)xo*(t)s1s3(z)G(s)s1s4为同步采样器H(s)b(t)xi*(t)b*(t)s2s4xi(t)3/22/2022102第六章 线性离散系统与z变换由图可知：Xo(s) G(s)*(s)B(s) H(s)Xo(s)(s)Xi(s) - B(s) = Xi(s) - H(s)G(s)*(s)两边取z变换：(z)Xi(z) - HG(z)(z)G(s)*

46、(s)* = G*(s)*(s)因此：)()(11)(zXzGHzi)()(1)()()()(zXzGHzGzzGzXio3/22/2022103第六章 线性离散系统与z变换输入作用下的偏差脉冲传递函数为：)(11)()()(zGHzXzzie与连续系统类似，闭环离散系统的特征方程定义为：D(z) 1 + GH(z) = 0其中， GH(z) 为该闭环离散系统的开环脉冲传递函数。所以，闭环脉冲传递函数为：)(1)()()()(zGHzGzXzXzio3/22/2022104第六章 线性离散系统与z变换需注意：)()(),()(sZzsZzee采用上述类似分析方法，可求得采样器位于其它位置时系统

47、的闭环脉冲传递函数。但只要偏差信号 (t) 处无采样开关，则输入信号xi*(t) (包括虚构的xi*(t) )便无法获得，从而不可能获得闭环离散系统对输入量的脉冲传递函数，尽管如此，仍有可能求出输出采样信号的 z 变换Xo(z)。3/22/2022105第六章 线性离散系统与z变换例如 考虑如下闭环离散系统：Xo(s) G(s)(s)，(s)Xi(s) - H(s)Xo*(s)(t)xo(t)xo*(t)s3G(s)H(s)xi(t)s1xo*(t)Xo(s) G(s)Xi(s) - G(s)H(s)Xo*(s)Xo(z)XiG(z) - GH(z)Xo(z)(1)()(zGHzGXzXio3

48、/22/2022106第六章 线性离散系统与z变换l 离散系统的过渡过程分析基本方法：z反变换法求输出序列xo*(t)。 单位阶跃响应例1：求图示系统的单位阶跃响应，其中采样周期T = 1s。Xi(s)*(s)Xo(s)s1(s)ses1) 1(1ss3/22/2022107第六章 线性离散系统与z变换解解：)(1)()(1)()()()(zGzGzGHzGzXzXzio)1(1)1 ()1(11)(21ssZzssseZzGsT)368. 0)(1(264. 0368. 0)(1()1 (1) 1(zzzezzeTzTeTTT1632. 0264. 0368. 0)()()(2zzzzzzX

49、zzXio632. 0264. 0368. 0)(2zzzz3/22/2022108第六章 线性离散系统与z变换32121632. 0632. 121264. 0368. 0zzzzz87654321868. 0802. 0895. 0147. 14 . 14 . 1368. 0zzzzzzzz按照采样点估算的近似性能指标：tr2stp4sts12sMp40%t (sec)xo*(t)0 1 2 3 4 5 6 7 8 9 1011121314151600.20.40.60.811.21.41.63/22/2022109第六章 线性离散系统与z变换 采样器与保持器对动态性能的影响考虑上例，若无

50、采样器与保持器，则系统为连续二阶系统，闭环传递函数为：11)(2sss若无采样器，只有保持器，闭环传递函数为：sTsTesses11)(233/22/2022110第六章 线性离散系统与z变换若只有采样器，无保持器，闭环脉冲传递函数为：)368. 0)(1(632. 0) 1(1)(zzzssZzG368. 0736. 0632. 0)(1)()(2zzzzGzGz3/22/2022111第六章 线性离散系统与z变换Step Responset (sec)01234567891000.20.40.60.811.21.41.6xo(t), xo*(t)连续系统无采样器无保持器采样保持 采样器使系

51、 统快速性提 高，稳定性 降低；但对 大延迟系统， 适当选择采 样周期可提 高稳定性。 保持器使系统快速性和稳定性均降低。3/22/2022112第六章 线性离散系统与z变换 采样周期对动态性能的影响Step Responset (sec)01234567891000.20.40.60.811.21.41.6xo*(t)T = 1sT = 0.5sT = 0.1s连续系统采样周期越大，快速性改善越好，但超调越大。3/22/2022113第六章 线性离散系统与z变换l 离散系统的稳态误差离散系统没有唯一的典型结构，给不出统一的误差脉冲传递函数形式，因而，其稳态误差需要针对不同形式的离散系统进行求

52、取。离散系统的稳态误差通常利用 z 变换的终值定理进行求解，所获得的误差是离散系统在采样瞬时的误差。离散系统稳态误差除与系统本身的结构、参数及输入形式有关外，还与采样周期 T 有关。3/22/2022114第六章 线性离散系统与z变换例1： 求图示系统在单位阶跃、单位速度以及单位加速度输入下的稳态误差，其中采样周期T = 1s。Xi(s)*(s)Xo(s)s1(s)ses1) 1(1ss3/22/2022115第六章 线性离散系统与z变换解解：图示系统为单位反馈系统，误差信号等于偏差信号，从而，可求得输入作用下的误差脉冲传递函数为：)(11)(11)()()()()(zGzGHzXzzXzEz

53、iie)368.0)(1(264.0368.0)1(11)(zzzssseZzGsT632. 0368. 0368. 1)()()(22zzzzzXzEzie3/22/2022116第六章 线性离散系统与z变换)(632. 0368. 0368. 1)(22zXzzzzzEi1）单位阶跃输入时1632. 0368. 0368. 1)(22zzzzzzzE0632. 0368. 0368. 1lim )() 1(lim)(2211zzzzzzEzezz3/22/2022117第六章 线性离散系统与z变换2）单位速度输入时22211) 1(632. 0368. 0368. 1) 1(lim )()

54、 1(lim)(zzzzzzzzEzezz22) 1() 1()(zzzTzzXi) 1)(632. 0()368. 0368. 1(lim221zzzzzzz1632. 143368. 0736. 23lim221zzzzz3/22/2022118第六章 线性离散系统与z变换3）单位加速度输入时22211) 1(2) 1(632. 0368. 0368. 1lim )() 1(lim)(zzzzzzzzEzezz332) 1(2) 1() 1(2) 1()(zzzzzzTzXi2221) 1)(632. 0(2)368. 0368. 1)(1(limzzzzzzzz264. 2264. 79

55、4368. 02104. 14lim2123231zzzzzzz3/22/2022119第六章 线性离散系统与z变换 离散系统的型别与静态误差系数离散系统的型别按照开环脉冲传递函数所具有的 z1的极点数v 进行划分。与连续系统类似， v0，1，2，的系统分别称为0型、I型、II型系统等。考虑常见的偏差采样闭环离散系统：(t)*(t)xo(t)s1G(s)H(s)xi(t)3/22/2022120第六章 线性离散系统与z变换q 稳态位置误差系数1)(zzzXi)(1lim1)(1lim 1)(11) 1(lim)(111zGHzGHzzzzGHzezzz)(1lim1zGHKzppKe1)(3/

56、22/2022121第六章 线性离散系统与z变换q 稳态速度误差系数2) 1()(zTzzXi)() 1(lim)(1) 1(lim 1)(11lim)(111zGHzTzGHzTzzTzzGHezzz)() 1(lim1zGHzKzvvKTe)(3/22/2022122第六章 线性离散系统与z变换q 稳态加速度误差系数32) 1(2) 1()(zzzTzXi)() 1(lim)(1) 1(2) 1(lim ) 1(2) 1()(11lim)(212221221zGHzTzGHzzzTzzzTzGHezzz)() 1(lim21zGHzKzaaKTe2)(3/22/2022123第六章 线性离

57、散系统与z变换五、离散系统的稳定性分析l s平面到z平面的映射TjTTjsTeeeez)(TzezTarg,|显然：01|01|01|zzz即z平面上的单位圆对应s平面的虚轴，单位圆内部对应左半s平面，外部对应右半s平面。3/22/2022124第六章 线性离散系统与z变换ReImsReImz00z1-/T/T3/T-3/T13/22/2022125第六章 线性离散系统与z变换注意到argz = T，若 = 0，当由-/T至/T变化时，z平面上的相应点从-逆时针变换到 (逆时针转一圈)。通常将-/T/T称为主频带。当由/T至3/T变化时， z平面上相应点再次逆时针转过一圈。因此， 由-至变化时

58、，z平面上的相应点沿单位圆转过无穷圈。3/22/2022126第六章 线性离散系统与z变换l 离散系统稳定的充要条件离散系统稳定的充要条件：离散系统闭环特征方程的所有特征根 zi 1 (i = 1, 2, 3, , n)均位于 z 平面的单位圆内，即|zi| 1。l 应用劳斯判据判别离散系统的稳定性劳斯判据只能用来判别复变量 s 的代数方程的根是否在虚轴的左面，不能判别特征根的模是否小于 1。3/22/2022127第六章 线性离散系统与z变换考虑如下的双线性变换（w变换）1111zzworwwz为此，需要对离散系统的特征方程进行坐标变换，将 z 平面的单位圆映射为另一复平面的虚轴，单位圆内部

59、映射到该平面虚轴的左面。令z = x + jy，w = u + jv ，则：3/22/2022128第六章 线性离散系统与z变换222222) 1(2) 1(1 11yxyjyxyxjyxjyxjvuw2222) 1(1yxyxu显然：1|101|101|10222222zyxifuzyxifuzyxifu注意到：3/22/2022129第六章 线性离散系统与z变换ReImwReImz00z1即双线性变换将 z 平面的单位圆映射到 w 平面的虚轴，单位圆内部映射到 w 平面虚轴的左面。3/22/2022130第六章 线性离散系统与z变换1111zzworwwz双线性变换（w变换）也可采用：例1

60、：分析图示系统稳定时K的取值范围，其中采样周期T = 1s。Xi(s)*(s)Xo(s)s1(s)sesT1)2( ssK3/22/2022131第六章 线性离散系统与z变换解解：由系统结构图有：)(1)()(1)()()()(zGzGzGHzGzXzXzio)2()1 ()(21ssKZzzG225. 025. 05 . 0)1 (21sssZzK TezzzzzTzzzK2225. 0125. 0) 1(5 . 01)(1(4)21 (1) 12(222TTTezzeTzTeK3/22/2022132第六章 线性离散系统与z变换系统特征方程为：1G(z) = 01353. 01353. 1