第三章力系的平衡

1、工工程程力力学学第第三三章章力力系系的的平平衡衡工程力学第三章第三章 力系的平衡力系的平衡工工程程力力学学第第三三章章力力系系的的平平衡衡汇交力系汇交力系F2F3FnF1平行力系平行力系F3F2F1F2F3FnF1任意力系任意力系空间力系空间力系F1F2Fn3-1 3-1 空间力系的平衡条件空间力系的平衡条件工工程程力力学学第第三三章章力力系系的的平平衡衡一、空间任意力系的平衡方程FR0，MO 0 =0,0,0()0,()0,()0 xyzxyzFFFMMMFFF空间任意力系平衡的必要与充分条件为：空间任意力系平衡的必要与充分条件为：力系中各力在三个力系中各力在三个坐标轴上投影的代数和等于零，

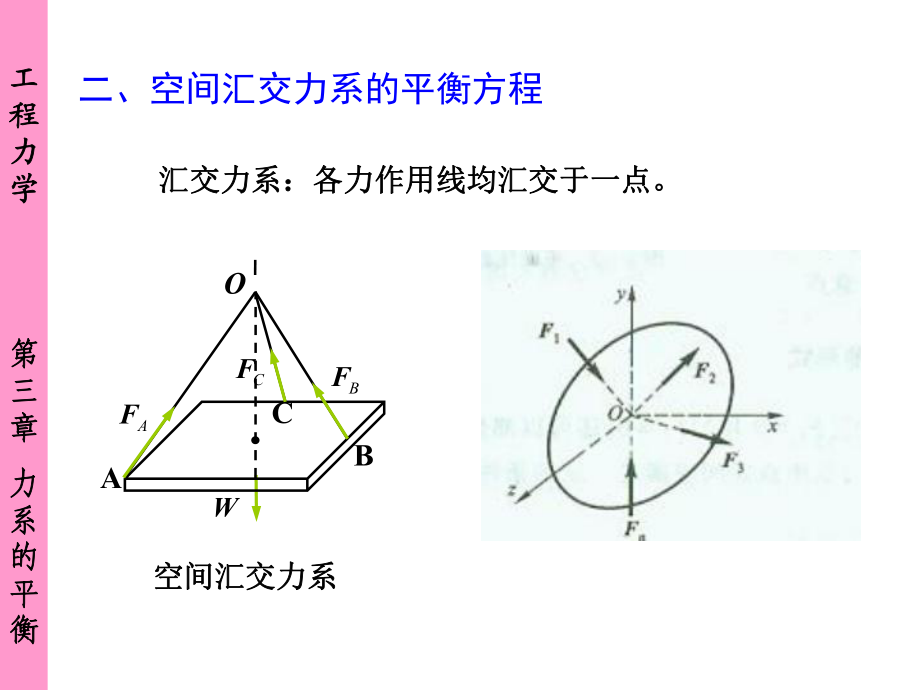
2、且各力对三个轴的矩的代数坐标轴上投影的代数和等于零，且各力对三个轴的矩的代数和也等于零。和也等于零。FnF1F2yzxOMOFROxyz工工程程力力学学第第三三章章力力系系的的平平衡衡汇交力系：各力作用线均汇交于一点。汇交力系：各力作用线均汇交于一点。AFCFBFWAOCB空间汇交力系空间汇交力系二、空间汇交力系的平衡方程工工程程力力学学第第三三章章力力系系的的平平衡衡0,xF 0,yF 0zF 即即: :汇交力系的平衡条件是汇交力系的平衡条件是力系中所有各力在各个坐力系中所有各力在各个坐标轴中每一轴上的投影的代数和分别等于零。标轴中每一轴上的投影的代数和分别等于零。2220RxyzFFFF汇

3、交力系平衡的充要条件是：汇交力系平衡的充要条件是：力系的合力等于零力系的合力等于零, ,即即: :工工程程力力学学第第三三章章力力系系的的平平衡衡三、空间平行力系的平衡方程0,zF ()0,xMF()0yMF工工程程力力学学第第三三章章力力系系的的平平衡衡即：力偶系各力偶矩矢分别在三个坐标轴投影的代数和为即：力偶系各力偶矩矢分别在三个坐标轴投影的代数和为零，称为力偶系作用下刚体的平衡方程。零，称为力偶系作用下刚体的平衡方程。000 xyzMMM0M 空间力偶系平衡的充分必要条件是空间力偶系平衡的充分必要条件是: :合力偶矩矢等于零，合力偶矩矢等于零，力偶系各力偶矩矢的矢量和等于零力偶系各力偶矩

4、矢的矢量和等于零 。写出解析的形式，有：写出解析的形式，有：222()()()RxyzMMMM四、空间力偶系的平衡方程工工程程力力学学第第三三章章力力系系的的平平衡衡平面任意力系平衡的充要条件是：平面任意力系平衡的充要条件是： 力系的主矢和对任意点的主矩都等于零。力系的主矢和对任意点的主矩都等于零。00RFM o 22 ()()( )RxyOOFFFMMF 平面任意力系的平衡方程：平面任意力系的平衡方程：000 xyoFFM1、平面任意力系的平衡方程、平面任意力系的平衡方程F2F3FnF1平面任意力系平面任意力系工工程程力力学学第第三三章章力力系系的的平平衡衡平面任意力系平衡方程的三种形式：平

5、面任意力系平衡方程的三种形式：刚体平衡条件刚体平衡条件二矩式二矩式A、B连线与连线与x轴不垂直轴不垂直三矩式三矩式A、B、C三点不共线三点不共线一矩式一矩式Fx =0Fy=0 MA=0Fx =0MA=0 MB=0MA=0M B=0 MC=0工工程程力力学学第第三三章章力力系系的的平平衡衡2、平面平行力系的平衡方程、平面平行力系的平衡方程平面平行力系的方程为两个，有两种形式：平面平行力系的方程为两个，有两种形式：00yoFM各力不得与投影轴垂直。各力不得与投影轴垂直。00BAMM两点连线不得与各力平行。两点连线不得与各力平行。BA,工工程程力力学学第第三三章章力力系系的的平平衡衡0yF 0,xF

6、 3、平面汇交力系的平衡方程、平面汇交力系的平衡方程4、平面力偶系的平衡条件、平面力偶系的平衡条件0M即：力偶系各力偶力偶矩的代数和等于零。即：力偶系各力偶力偶矩的代数和等于零。工工程程力力学学第第三三章章力力系系的的平平衡衡求解平衡问题的步骤求解平衡问题的步骤1、选择合适的平衡对象，从系统中隔离；、选择合适的平衡对象，从系统中隔离；2、进行受力分析；、进行受力分析；3、应用平衡方程进行求解、应用平衡方程进行求解工工程程力力学学第第三三章章力力系系的的平平衡衡例：圆弧杆例：圆弧杆AB与折杆与折杆BDC在在B处铰接，处铰接，A、C两处均为固定两处均为固定铰支座，结构受力如图所示。试求铰支座，结构

7、受力如图所示。试求A、C两处的约束力。两处的约束力。工工程程力力学学第第三三章章力力系系的的平平衡衡例：平面钢架受力及各部分尺寸如图所示，所有外力的作例：平面钢架受力及各部分尺寸如图所示，所有外力的作用线都位于钢架平面内。用线都位于钢架平面内。A处为固定端约束，求处为固定端约束，求A处约束力。处约束力。工工程程力力学学第第三三章章力力系系的的平平衡衡例：图示结构中，例：图示结构中，A、B、C三处均为铰链约束。横杆三处均为铰链约束。横杆AB在在B处承受集中载荷处承受集中载荷F。试求撑杆。试求撑杆CD的受力及的受力及A处的约束力。处的约束力。工工程程力力学学第第三三章章力力系系的的平平衡衡例：图中

8、所示结构，例：图中所示结构，AB、AC、AD三杆由活动球铰连接于三杆由活动球铰连接于A处；处；B、C、D三处均为固定球铰支座。在三处均为固定球铰支座。在A处悬挂重物，处悬挂重物，重物的重量重物的重量W为已知。试求三杆的受力。为已知。试求三杆的受力。工工程程力力学学第第三三章章力力系系的的平平衡衡例：如图所示为水利涡轮发电机中的主轴。水力推动涡轮例：如图所示为水利涡轮发电机中的主轴。水力推动涡轮转动的力偶矩转动的力偶矩M=1200N.m。在锥齿轮。在锥齿轮B处受到的力分解为处受到的力分解为三个分立：圆周力，轴向力和径向力。三者大小的比例为三个分立：圆周力，轴向力和径向力。三者大小的比例为1:0.

9、32:0.17。已知涡轮连同轴和锥齿轮的总重量为。已知涡轮连同轴和锥齿轮的总重量为W=12Kn，其作用线沿轴其作用线沿轴Cz；锥齿轮的平均半径；锥齿轮的平均半径OB=0.6m ，试求止推，试求止推轴承轴承C和轴承和轴承A的反力。的反力。工工程程力力学学第第三三章章力力系系的的平平衡衡 塔式起重机的结构简图如塔式起重机的结构简图如图所示。起重机自重为图所示。起重机自重为W，载，载重为重为W1，平衡物重，平衡物重W2。要使。要使起重机在空载、满载且载重在起重机在空载、满载且载重在最远处时均不翻到，试求平衡最远处时均不翻到，试求平衡物重。物重。解：解：（1）取塔式起重机整体为研究对象）取塔式起重机整

10、体为研究对象,受力分析如图。受力分析如图。（整机在平面平行力系作用下处于平衡。）（整机在平面平行力系作用下处于平衡。）2W1WWeCbla例：翻到问题例：翻到问题工工程程力力学学第第三三章章力力系系的的平平衡衡( (2) ) 列平衡方程：列平衡方程：0,AM0BF 1) 空载时（空载时（ W1 =0）：）：不翻倒的条件是：不翻倒的条件是：B2()0Fb W ebWa B21()0FW ebWab可得空载时平衡物重量可得空载时平衡物重量W2的条件：的条件：2()W ebWa2W1WWeCbla工工程程力力学学第第三三章章力力系系的的平平衡衡0,BM0AF 2) 满载且载重位于最远端时满载且载重位

11、于最远端时,不翻到不翻到的条件是：的条件是：A21()0FbW abWe W l A121()0FWe WlWabb 211()WWeWlab2W1WWeCbla121()()W ebWeWlWaba综合考虑，平衡物重量综合考虑，平衡物重量W2应满载的条件应满载的条件：可得满载时平衡物重量可得满载时平衡物重量W2的条件：的条件：工工程程力力学学第第三三章章力力系系的的平平衡衡解：解：（1）取汽车及起重机为研究对象）取汽车及起重机为研究对象,受力分析如图。受力分析如图。例例7 ： 翻到问题翻到问题 （自学）（自学） 一种车载式起重机，车重一种车载式起重机，车重Q = 26kN，起重机伸臂重，起重

12、机伸臂重G= 4.5kN，起重机的旋转部分与固定部分共重，起重机的旋转部分与固定部分共重W = 31kN。尺。尺寸如图所示，单位是寸如图所示，单位是m，设伸臂在起重机对称面内，且放，设伸臂在起重机对称面内，且放在图示位置，试求车子不致翻倒的最大起重量在图示位置，试求车子不致翻倒的最大起重量Pmax。AB3.02.51.82.0AFFBQWGP工工程程力力学学第第三三章章力力系系的的平平衡衡122.55.53.8AFQGP0,yF 0ABFFPQGW 0,BMF 5.52.523.80APGQF（3）联立求解：）联立求解： （2）列平衡方程：）列平衡方程：（4）不翻条件：）不翻条件：FA0122

13、.57.55.5PQGkN由由上上式式可可得得 故故最大起重重量为最大起重重量为 Pmax= 7.5 kNAB3.02.51.82.0AFFBQWGP工工程程力力学学第第三三章章力力系系的的平平衡衡 一、静定与静不定的概念一、静定与静不定的概念静定问题静定问题未知量数目未知量数目NR不超出不超出独立独立平衡方程的数目平衡方程的数目NE静不定问题静不定问题未知量数目未知量数目NR超出超出独立独立平衡方程的数目平衡方程的数目NENR NE自由度数自由度数NRNE静不定次数静不定次数N = NE - NRI = NR -NE3-4 物体系统的平衡物体系统的平衡静定与静不定的概念静定与静不定的概念工工

14、程程力力学学第第三三章章力力系系的的平平衡衡静定静定静不定静不定静定静定静不定静不定静不定静不定NR=3NE =3NE =3NE =2NE =3NE =3NR=3NR=3NR=4NR=4静定静定NE =3NR=3工工程程力力学学第第三三章章力力系系的的平平衡衡BCPQANR = 4+2=6NE = 2 3=6NR =5+2=7NE = 2 3=6NR = 5+1=6NE = 2 3=6静定静定静定静定静不定静不定YAXAYBXBYAXAACPXCYCYBXBBCQXCYC刚体系统刚体系统工工程程力力学学第第三三章章力力系系的的平平衡衡1、整体平衡与局部平衡的概念、整体平衡与局部平衡的概念 系统

15、如果整体是平衡的，则组成系统的每一个局系统如果整体是平衡的，则组成系统的每一个局部以及每一个刚体也必然是平衡的。部以及每一个刚体也必然是平衡的。二、刚体系统平衡问题的特点二、刚体系统平衡问题的特点2、研究对象有多种选择、研究对象有多种选择 一般先整体后局部一般先整体后局部3、对刚体系统作受力分析时，要分清内力和外力、对刚体系统作受力分析时，要分清内力和外力4、每个刚体上的力系都必须满足平衡条件、每个刚体上的力系都必须满足平衡条件工工程程力力学学第第三三章章力力系系的的平平衡衡三、刚体系的平衡问题的解法三、刚体系的平衡问题的解法1、刚体系平衡问题的基本步骤：、刚体系平衡问题的基本步骤：选择研究对

16、象；选择研究对象；取分离体画受力图；取分离体画受力图；列平衡方程；列平衡方程；求解。求解。2、物体系平衡方程的数目：、物体系平衡方程的数目： 由由n个物体组成的物体系，总共有不多于个物体组成的物体系，总共有不多于3n个独个独立的平衡方程；如有汇交力系和平行力系，平衡方程立的平衡方程；如有汇交力系和平行力系，平衡方程数目减少。数目减少。工工程程力力学学第第三三章章力力系系的的平平衡衡例：所示结构由杆例：所示结构由杆AB与与BC在在B处铰接而成。结构处铰接而成。结构A处为固定端，处为固定端，C处为辊轴支座。结构在处为辊轴支座。结构在DE段承受均布载荷作用，载荷集度为段承受均布载荷作用，载荷集度为q

17、; E 处作用有外加力偶，其力偶矩为处作用有外加力偶，其力偶矩为M。q 、M、l等均为已知。等均为已知。试求试求A、C两处的约束力。两处的约束力。工工程程力力学学第第三三章章力力系系的的平平衡衡例：如图所示为一种起吊装置的结构简图。图中尺寸例：如图所示为一种起吊装置的结构简图。图中尺寸d , 载荷载荷F， FAD =60均为已知。若不计各杆自重，试求杆均为已知。若不计各杆自重，试求杆AF与杆与杆AD在各在各自的约束处所受的约束力。自的约束处所受的约束力。工工程程力力学学第第三三章章力力系系的的平平衡衡工工程程力力学学第第三三章章力力系系的的平平衡衡例：滑轮支架系统如图所示。已知例：滑轮支架系统

18、如图所示。已知G G，a,r,a,r,其余物体重其余物体重量不计量不计, ,试求试求A A和和B B的约束力。的约束力。工工程程力力学学第第三三章章力力系系的的平平衡衡0,2(2)(2)2oAyTAyMFaFarGarFG 0,00,2 tan(4)00,0yAyByABxxAxBxFFFGMFaGarFFF3 ,(4)cos/(2 sin ),(4)cos/(2 sin )ByBxAxBxFG FGaraFFGara 1、研究杆、研究杆AC和滑轮重物系统和滑轮重物系统2、研究整体、研究整体工工程程力力学学第第三三章章力力系系的的平平衡衡例例： 梁梁ACB如图。梁上起重小车重如图。梁上起重小车重W=50kN，吊，吊 重重 P=10kN，求，求A、B处的约束力。处的约束力。由由(1)知，知，FAx=0。剩余二个方程中含三个未知约束反力，不足以求解。剩余二个方程中含三个未知约束反力，不足以求解。 列平衡方程：列平衡方程： Fx=FAx=0 -(1) Fy=FAy+FBy-P-W=0 -(2) MA(F) =MA+12FBy-4W-8