资源目录

压缩包内文档预览:
编号:10061562
类型:共享资源
大小:4.96MB
格式:ZIP
上传时间:2018-04-30
上传人:机****料
认证信息
个人认证
高**(实名认证)
河南
IP属地:河南
50
积分
- 关 键 词:
-
平板
闸门
设计
全套
cad
图纸
- 资源描述:
-





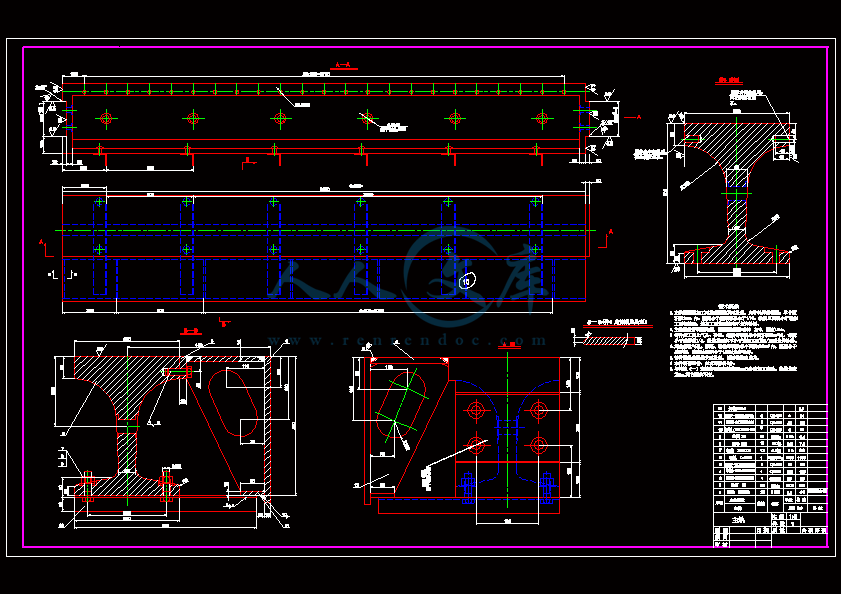




- 内容简介:
-
ABSTRACTPARTIIIOFTHISTHREEPARTSERIESOFPAPERSDESCRIBESTHESYNTHESISOFROLLERANDSLIDINGHYDRAULICSTEELGATESTRUCTURESPERFORMEDBYTHEMIXEDINTEGERNONLINEARPROGRAMMINGMINLPAPPROACHTHEMINLPAPPROACHENABLESTHEDETERMINATIONOFTHEOPTIMALNUMBEROFGATESTRUCTURALELEMENTSGIRDERS,PLATES,OPTIMALGATEGEOMETRY,OPTIMALINTERMEDIATEDISTANCESBETWEENSTRUCTURALELEMENTSANDALLCONTINUOUSANDSTANDARDCROSSECTIONALSIZESFORTHISPURPOSE,SPECIALLOGICALCONSTRAINTSFORTOPOLOGYALTERATIONSANDINTERCONNECTIONRELATIONSBETWEENTHEALTERNATIVEANDFIXEDSTRUCTURALELEMENTSAREFORMULATEDTHEYHAVEBEENEMBEDDEDINTOAMATHEMATICALOPTIMIZATIONMODELFORROLLERANDSLIDINGSTEELGATESTRUCTURESGATOPGATOPHASBEENDEVELOPEDACCORDINGTOASPECIALMINLPMODELFORMULATIONFORMECHANICALSUPERSTRUCTURESMINLPMS,INTRODUCEDINPARTSIANDIITHEMODELCONTAINSANECONOMICOBJECTIVEFUNCTIONOFSELFMANUFACTURINGANDTRANSPORTATIONCOSTSOFTHEGATEASTHEGATOPMODELISNONCONVEXANDHIGHLYNONLINEAR,ITISSOLVEDBYMEANSOFTHEMODIFIEDOA/ERALGORITHMACCOMPANIEDBYTHELINKEDTWOPHASEMINLPSTRATEGY,BOTHIMPLEMENTEDINTHETOPCOMPUTERCODEANEXAMPLEOFTHESYNTHESISISPRESENTEDASACOMPARATIVEDESIGNRESEARCHWORKOFTHEALREADYERECTEDROLLERGATE,THESOCALLEDINTAKEGATEINASWANIIINEGYPTTHEOPTIMALRESULTYIELDS294PERCENTOFNETSAVINGSWHENCOMPAREDTOTHEACTUALCOSTSOFTHEERECTEDGATE1998JOHNWILEYOPTIMIZATIONTOPOLOGYOPTIMIZATIONDISCRETEVARIABLEOPTIMIZATIONMIXEDINTEGERNONLINEARPROGRAMMINGMINLPTHEMODIFIEDOA/ERALGORITHMMINLPSTRATEGYHYDRAULICGATESLIDINGGATEROLLERGATEASWAN1INTRODUCTIONTHISPAPERDESCRIBESTHEMIXEDINTEGERNONLINEARPROGRAMMINGMINLPAPPROACHTOTHESYNTHESISOFROLLERANDSLIDINGGATESTRUCTURES,IETHESIMPLESTTYPESAMONGVERTICALLIFTHYDRAULICSTEELGATES,SEEFIGURE1ROLLERANDSLIDINGGATESAREALSOREGARDEDASTHEMOSTFREQUENTLYMANUFACTUREDTYPESOFHYDRAULICSTEELGATESFORHEADWATERCONTROLTHEYAREUSEDTOREGULATETHEWATERSTREAMONHYDROELECTRICPLANTS,DAMSORSPILLWAYSASHYDRAULICSTEELGATESAREVERYSPECIALSTRUCTURES,ONLYAFEWAUTHORSHAVEDISCUSSEDTHEIROPTIMIZATION,EGKRAVANJAETAL,1DJONGELINGANDKOLKMANASWELLASALMQUISTETALPARTICULARINTERESTWASSHOWNINTHEOPTIMIZATIONNOTOFTHESEROLLERANDSLIDINGGATESBUTOFSIMILARSTRUCTURESINSUCHINVESTIGATIONS,VANDERPLAATSANDWEISSHAARASWELLASGURDALETALOPTIMIZEDSTIFFENEDLAMINATEDCOMPOSITEPANELS,BUTLERANDRINGERTZOPTIMIZEDSTIFFENEDPANELS,FARKASANDJARMAI1OPTIMIZEDWELDEDRECTANGULARCELLULARPLATES,FINCKENORETAL1TREATEDSKINSTRINGERCYLINDERSANDGENDYETAL1STIFFENEDPLATESALMOSTALLAUTHORSUSEDNONLINEARPROGRAMMINGNLPTECHNIQUESGURDALETALPROPOSEDTHEGENETICALGORITHM,WHILEKRAVANJAETAL1DINTRODUCEDMINLPALGORITHMSANDSTRATEGIESTOTHESIMULTANEOUSTOPOLOGYANDPARAMETEROPTIMIZATIONOFTHEGATEINPARTSIOFTHISTHREEPARTSERIESOFPAPERS,AGENERALVIEWOFTHEMINLPAPPROACHTOTHESIMULTANEOUSTOPOLOGYANDPARAMETEROPTIMIZATIONOFSTRUCTURESISPRESENTEDPARTIIDESCRIBESTHEEXTENSIONTOTHESIMULTANEOUSSTANDARDDIMENSIONOPTIMIZATIONBASEDONTHESUPERSTRUCTUREAPPROACHDEFINEDINPARTSIANDII,THEMAINOBJECTIVEOFTHISPAPERPARTIIIISTHEMINLPSYNTHESISOFROLLERANDSLIDINGHYDRAULICSTEELGATESTRUCTURES,OBTAINEDATMINIMALGATECOSTSANDSUBJECTEDTODEFINEDDESIGN,MATERIAL,STRESS,DEFLECTIONANDSTABILITYCONSTRAINTSASTHEMINLPAPPROACHENABLESSIMULTANEOUSTOPOLOGY,PARAMETERANDSTANDARDDIMENSIONOPTIMIZATION,ANUMBEROFGATESTRUCTURALELEMENTSGIRDERSANDPLATES,THEGATEGLOBALGEOMETRY,INTERMEDIATEDISTANCESBETWEENSTRUCTURALELEMENTSANDALLCONTINUOUSANDSTANDARDDIMENSIONSAREOBTAINEDSIMULTANEOUSLYTHISLASTPARTOFTHETHREEPARTSERIESOFPAPERSISDIVIDEDINTOTHREEMAINSECTIONS1SECTION2DESCRIBESHOWDIFFERENTTOPOLOGYANDSTANDARDDIMENSIONALTERNATIVESAREPOSTULATEDANDHOWTHEIRINTERCONNECTIONRELATIONSAREFORMULATEDBYMEANSOFEXPLICITLOGICALCONSTRAINTSINORDERTOPERFORMTOPOLOGYANDSTANDARDDIMENSIONALTERATIONSWITHINTHEOPTIMIZATIONPROCEDURE2SECTION3REPRESENTSAGENERALMINLPOPTIMIZATIONMODELFORROLLERANDSLIDINGGATESTRUCTURESGATOP3FINALLY,INSECTION4,THEPROPOSEDSUPERSTRUCTUREMINLPAPPROACHISAPPLIEDTOTHESYNTHESISOFANALREADYERECTEDROLLERGATE,THESOCALLEDINTAKEGATEINASWANIIINEGYPT2SUPERSTRUCTUREALTERNATIVESANDTHEMODELLINGOFTHEIRDISCRETEDECISIONS21POSTULATIONOFTOPOLOGYANDSTANDARDDIMENSIONALTERNATIVESTHEFIRSTSTEPINTHESYNTHESISOFTHEGATEISTHEGENERATIONOFANMINLPSUPERSTRUCTUREINWHICHDIFFERENTTOPOLOGY/STRUCTUREANDSTANDARDDIMENSIONALTERNATIVESAREEMBEDDEDTOBESELECTEDASTHEOPTIMALRESULTTHEGATESUPERSTRUCTUREALSOCONTAINSTHEREPRESENTATIONOFSTRUCTURALELEMENTSWHICHMAYCONSTRUCTEACHPOSSIBLESTRUCTUREALTERNATIVEASWELLASDIFFERENTSETSOFDISCRETEVALUES,DEFINEDFOREACHSTANDARDDIMENSIONALTERNATIVEASBOTHTHEROLLERANDSLIDINGGATESHAVEALMOSTTHESAMESTRUCTURE,ITWASREASONABLETOPROPOSEASUPERSTRUCTURE,WHICHCOULDWELLBEUSEFULFORBOTHOFTHEM211TOPOLOGYALTERNATIVESTHEGATESUPERSTRUCTURETYPICALLYINCLUDESAREPRESENTATIONOFMAINGATEELEMENTS,WHEREEACHGATEELEMENTISCOMPOSEDOFVARIOUSSTRUCTURALELEMENTS,SUCHASHORIZONTALGIRDERS,VERTICALGIRDERS,STIFFENERSANDPLATEELEMENTSOFTHESKINPLATE,SEEFIGURE2THESUPERSTRUCTURECOMPRISESNMAINGATEELEMENTS,N3N,EACHCONTAININGMHORIZONTALGIRDERS,M3M,THE32VNUMBEROFVERTICALGIRDERSTHROUGHTHEENTIREGATE,V3,ANDTHECORRESPONDINGM122VNUMBEROFSKINPLATEELEMENTSTOEACHMTHHORIZONTALGIRDEROFTHENTHMAINGATEELEMENTANEXTRABINARYVARIABLEYN,MISASSIGNEDTHENUMBEROFHORIZONTALGIRDERSANDCORRESPONDINGPLATEELEMENTSOFTHESKINPLATE,DISTRIBUTEDOVERTHENTHMAINGATEELEMENT,CANTHEREFOREBEDETERMINEDSIMPLYBYNOTE,MNYTHATTHEPROPOSEDMINIMALNUMBEROFIDENTICALVERTICALGIRDERSIS3ANDTHATTHEYCANTAKEONLYODDNUMBERSIFABINARYVARIABLEYVISASSIGNEDTOEACHV,VV,THENUMBEROFVERTICALGIRDERSCANBEOBTAINEDBY32VYVINTHESAMEWAYANEVENNUMBER22VYVOFEQUALHORIZONTALPARTITIONSOFTHEENTIREGATEISPROPOSEDINTHECASEOFVERTICALGIRDERS,WECANSEETHATTHESTRUCTURALELEMENTSCANALSOBEDETERMINEDBYSUITABLELINEARCOMBINATIONSOFBINARYVARIABLESAMONGTHEMAXIMALNUMBERMMAXOFHORIZONTALGIRDERSPEREACHMAINGATEELEMENT,THEUPPERANDLOWERGIRDERSTOGETHERWITHTHEMINIMALNUMBERMMINOFINTERMEDIATEHORIZONTALGIRDERSANDTHEADJOININGSKINPLATEELEMENTSARETREATEDASFIXEDSTRUCTURALELEMENTS,WHICHAREALWAYSPRESENTINTHEOPTIMIZATIONALLOTHERMMAXMMININTERMEDIATEHORIZONTALGIRDERSWITHTHECORRESPONDINGNUMBEROFADJOINEDSKINPLATEELEMENTSARETHENREGARDEDASALTERNATIVESTRUCTURALELEMENTS,WHICHMAYEITHERDISAPPEARORBESELECTEDSINCEONLYALTERNATIVESTRUCTURALELEMENTSPARTICIPATEINTHEDISCRETEOPTIMIZATION,THESIZEOFTHEDISCRETEDECISIONSISSIGNIFICANTLYREDUCEDEACHPOSSIBLECOMBINATIONBETWEENSELECTEDALTERNATIVESTRUCTURALELEMENTSANDFIXEDSTRUCTURALELEMENTSFORMSANEXTRAGATETOPOLOGY/STRUCTUREALTERNATIVE212STANDARDDIMENSIONALTERNATIVESFOURSTANDARDDIMENSIONSAREADDITIONALLYDEFINEDTOREPRESENTTHESTANDARDTHICKNESSESOFSHEETIRONPLATESTHETHICKNESSOFTHESKINPLATETSNFOREACHNTHMAINGATEELEMENT,THEFLANGETHICKNESSOFTHEHORIZONTALGIRDERTFN,THEWEBTHICKNESSOFTHEOUTERHORIZONTALGIRDERM1OR,OUTWNMMM,ANDTHEWEBTHICKNESSOFTHEINNERHORIZONTALGIRDER,1MMIT,SINCETHETHICKNESSTSNHASACOMMONVALUEFORTHEENTIRESKINPLATEOFTHENTHMAINGATEELEMENTANDTHETARETHESAMEFORALLHORIZONTALGIRDERSOFTHENTHMAINGATEELEMENT,IETHEYCORRESPONDTOTHECOMMONSTANDARDDESIGNVARIABLESFORTHESUPERSTRUCTUREORITSPARTFROMTHESPECIAL,STCOMDMINLPMSMODELFORMULATIONINPARTIISIMILARLY,THEWEBTHICKNESSES,WHICHTAKEACOMMONVALUEFORBOTHOUTERHORIZONTALGIRDERSOFTHEOUTWNMNTHMAINGATEELEMENT,AND,WHICHARETHESAMEFORALLTHEINNERINWMTHORIZONTALGIRDERS,CORRESPONDTOTHECOMMONSTANDARDDESIGNVARIABLESOFTHEALTERNATIVESTRUCTURALELEMENTSANEXTRASETOFDISCRETEVALUES,STCOMADOFSTANDARDDIMENSIONALTERNATIVESANDASPECIALSETOFTHESAMESIZEOFBINARYVARIABLESAREINTRODUCEDFOREACHMENTIONEDSTANDARDDIMENSIONEACHSTANDARDDIMENSIONTSNSHALLBEEXPRESSEDWITHINTHEGIVENISTANDARDDIMENSIONALTERNATIVES,II,STANDARDDIMENSIONTFNBYKALTERNATIVES,KK,STANDARDDIMENSIONBYPALTERNATIVES,PP,ANDSTANDARD,OUTWNMDIMENSIONBYRALTERNATIVES,RRTHEVECTOROFIBINARYVARIABLES,INWMTYN,IANDTHEVECTOROFIDISCRETEVALUESQN,IAREASSIGNEDTOTHEVARIABLETSN,THEVECTORSOFKELEMENTSYN,KANDQN,KTOTHEVARIABLETFN,THEVECTORSOFPELEMENTSYN,PANDQN,KTOTHEVARIABLEANDTHEVECTORSOFRELEMENTS,INWMTYN,VANDQN,VTOTHEVARIABLECONSEQUENTLY,THEOVERALLVECTOROFBINARY,INWMTVARIABLESASSIGNEDTOTHEGATESUPERSTRUCTUREISYYN,M,Y,V,YN,I,YN,P,YN,V22MODELINGOFDISCRETEDECISIONSTHEPOSTULATEDGATESUPERSTRUCTUREOFTOPOLOGYANDSTANDARDDIMENSIONALTERNATIVESCANBEFORMULATEDASANMINLPPROBLEMUSINGASPECIALMINLPMODELFORMULATIONMINLPMSFORSIMULTANEOUSTOPOLOGY,PARAMETERANDSTANDARDDIMENSIONOPTIMIZATIONOFMECHANICALSUPERSTRUCTURES,DESCRIBEDINPARTIIASCANBESEENFROMTHEMINLPMS,THEOBJECTIVEFUNCTIONISTYPICALLYSUBJECTEDTOSTRUCTURALANALYSISANDLOGICALCONSTRAINTSWHILESTRUCTURALANALYSISCONSTRAINTSREPRESENTAMATHEMATICALMODELOFASYNTHESIZEDSTRUCTURE,LOGICALCONSTRAINTSAREUSEDFORTHEEXPLICITMODELINGOFLOGICALDECISIONSMODELINGOFDISCRETEDECISIONSTODETERMINETOPOLOGYALTERNATIVESISANOBJECTIVEOFTHEHIGHESTIMPORTANCEFORTHESYNTHESISINORDERTOPERFORMTHESEDECISIONSWITHINTHEMINLPOPTIMIZATION,INTERCONNECTIONLOGICALCONSTRAINTSDYRD,PRAREPROPOSEDWHILEVARIABLES,THEIRBOUNDSANDMOSTOFTHECONSTRAINTSOFTHEMINLPMSMODELFORMULATIONAREREPRESENTEDINPARTII,INTERCONNECTIONLOGICALCONSTRAINTSANDTHECONSTRAINTSDEFININGTOPOLOGYALTERATIONSAREDESCRIBEDINTHISSECTIONTHELATTERONESAREDERIVEDFROMTHEFOLLOWINGBASICINTEGERORMIXEDINTEGERLOGICALCONSTRAINTSAMULTIPLECHOICECONSTRAINTSFORSELECTINGAMONGASETOFUNITSISELECTEXACTLYMUNITS1IIYSELECTMUNITSATTHEMOST2IIMSELECTATLEASTMUNITS3IIYBIFTHENCONDITIONSIFUNITKISSELECTEDTHENUNITIMUSTBESELECTEDYKYI04CACTIVATIONORDEACTIVATIONOFCONTINUOUSVARIABLES,INEQUALITIESOREQUATIONS1EXAMPLETORELATECONTINUOUSVARIABLEXTOTHESCALARVALUEUXUY5IF1,0YXUIFYX2ANOPPOSITERELATIONXU(1Y)610,YXIFYXU3EXAMPLEFORTHEBOUNDSOFCONTINUOUSVARIABLEXX1,0YXXUPY7IF1,0,0UPYXIFYXDINTEGERCUTSCONSTRAINTELIMINATESUNNECESSARYINTEGERCOMBINATIONSYK0,1MEGTHOSEFOUNDATPREVIOUSMINLPITERATIONS,1,I8K|BIKKIIIBINIYWHERE,I|KI|Y0INORDERTODESCRIBETHEMODELINGOFDISCRETEDECISIONS,AGENERALGATESUPERSTRUCTUREFROMFIGURE2ISADDRESSEDINWHICHTHEDEFINEDSTRUCTURALELEMENTSARETYPICALLYHORIZONTALANDVERTICALGIRDERSASTHEMODELINGOFVERTICALGIRDERSISSIMPLIFIEDANDNEEDSNOSPECIALINTERCONNECTIONLOGICALCONSTRAINTS,THEMODELINGOFDISCRETEDECISIONSREGARDINGHORIZONTALGIRDERSPROVEDTOBEMORESOPHISTICATED221MODELINGOFTOPOLOGYALTERATIONSLETUSCONSIDERTHEVERTICALCROSSSECTIONOFTHEGATEELEMENTSUPERSTRUCTUREWITHFIXEDANDALTERNATIVEHORIZONTALGIRDERS,SEEFIGURE3ATHENUMBEROFFIXEDANDALTERNATIVEGIRDERSANDTHEIRLOCATIONSINTHESUPERSTRUCTURECANBEDESCRIBEDBYTHEFOLLOWINGLOGICALCONSTRAINTS9MINMAXMY101,23,111MAXYLOGICALCONSTRAINT9DEFINESTHEMINIMALMMINANDMAXIMALMMAXNUMBEROFSTRUCTURALELEMENTSGIRDERSWHILENUMBERMMINREPRESENTSTHENUMBEROFFIXEDSTRUCTURALELEMENTS,THEDIFFERENCEBETWEENTHEMAXIMALANDMINIMALNUMBEROFELEMENTSMMAXMMINGIVESTHENUMBEROFALTERNATIVESTRUCTURALELEMENTSCONSTRAINT10DEFINESTHEDIRECTIONOFTHEREMOVALOFALTERNATIVEELEMENTSFROMTHETOPDOWNTHESUPERSTRUCTUREFROMFIGURE3ISEVIDENTTHATTHEMOSTUPPERELEMENTISTHEFIXEDONE,WHICHISSETBYTHECONSTRAINT11ITTHENFURTHERFOLLOWSFROMCONSTRAINT10THATALLTHERESTFIXEDELEMENTSARELOCATEDATTHEBOTTOMOFTHESUPERSTRUCTUREHENCE,CONSTRAINTS911REPRESENTTHEEXPLICITMODELFORTOPOLOGYALTERATIONSOFHORIZONTALGIRDERS222MODELINGOFINTERCONNECTIONRELATIONSINTERCONNECTIONRELATIONSBETWEENALTERNATIVEANDFIXEDSTRUCTURALELEMENTSWITHINTHESUPERSTRUCTUREREQUIRESPECIALATTENTIONPAIDTOTHESTRUCTURALSYNTHESISPERFORMEDBYTHEMINLPAPPROACHINTERCONNECTIONRELATIONSEITHERRESTORETHECONNECTIONSBETWEENCURRENTLYSELECTEDEXISTINGSTRUCTURALELEMENTSORCANCELTHERELATIONSBETWEENCURRENTLYREJECTEDDISAPPEARINGSTRUCTURALELEMENTSSINCEMINLPMETHODSOPTIMIZETHETOPOLOGYANDPARAMETERSSIMULTANEOUSLY,ITISNECESSARYTODEFINETHESEINTERCONNECTIONRELATIONSINANEXPLICITEEQUATIONALFORM,SOTHATTHEYCANENABLEINTERCONNECTIONSANDDISCONNECTIONSBETWEENTHEELEMENTSDURINGTHEOPTIMIZATIONPROCESSSPECIALINTERCONNECTIONLOGICALCONSTRAINTSFORINTERCONNECTIONRELATIONSBETWEENTHEALTERNATIVEANDFIXEDSTRUCTURALELEMENTSHAVEBEENPROPOSEDTHEYWILLBEEMBEDDEDINTOTHEMINLPOPTIMIZATIONMODELOFTHEGATESTRUCTURE,ENABLINGTHELATTERTOTHUSBECOMESELFSUFFICIENTFORAUTOMATICTOPOLOGYANDPARAMETEROPTIMIZATIONTHEMODELINGOFINTERCONNECTIONLOGICALCONSTRAINTS,HOWEVER,REQUIRESADDITIONALEFFORT,SINCEMOSTELEMENTCONSTRAINTSINCLUDEFUNCTIONSNOTONLYOFTHEIROWNVARIABLESBUTALSOOFTHEVARIABLESBELONGINGTOTHEIRADJOININGSTRUCTURALELEMENTSSUCHANEXAMPLEIS,EGTHECONSTRAINTOFTHEMOMENTOFINERTIAIN,MOFTHEMTHHORIZONTALGIRDEROFTHENTHMAINGATEELEMENTSEEEQUATION23INTHEFOLLOWINGSECTION,WHICHINCLUDESTHESUBSTITUTEDEXPRESSIONS6OFTHESKINPLATEEFFECTIVEWIDTHWITHTHE,NMSBHEIGHTSBETWEENGIRDERSANDTHESILLHM1ANDHM1OFBOTHADJOININGGIRDERSTHECONSTRAINTSOFTHEMTHINTERMEDIATEHORIZONTALGIRDERARETYPICALLYFUNCTIONSOFTHREEHEIGHTSHM1,HMANDHM1,ANDTWOVERTICALDISTANCESBETWEENHORIZONTALGIRDERS,ANDTHEDISTANCEIS1D1DMHDSIMPLYDEFINEDBYTHECONSTRAINTM2,3,M1121MHDTHEPROBLEMARISESIFHM1ISNOTDEFINEDWHENTHEADJOININGUPPERALTERNATIVEGIRDERTOTHEMTHHORIZONTALGIRDERDOESNOTEXISTFOREXAMPLE,LETUSCONSIDERTHETHIRDGIRDERINFIGURE3AWHICHISTHEUPPERMOSTEXISTINGINTERMEDIATEELEMENTINORDERTODEFINEH4SOASTOFULFILTHECONSTRAINTSOFGIRDER3,H4SHOULDTEMPORARILYBECOMEEQUALTOTHEHEIGHTOFTHEUPPERMOSTFIXEDGIRDERH6HMFIGURE3BTHEMAINIDEAISTOSETALLHEIGHTSOFNONEXISTINGINTERMEDIATEGIRDERSGIRDERS4AND5INFIGURE3ATOTHEVALUEOFH6BYMEANSOFTHELOGICALCONSTRAINTS,M2,3,M113MUPHDY,M2,3,M114,LOWEXNOTE,THATCONSTRAINTS13AND14RESTORETHEUPPERANDLOWERMUPHD,MLOWEXHDBOUNDSOFTHEDISTANCEWHENTHECORRESPONDINGGIRDEREXISTSYM1MHDANDSETITTOZERO,OTHERWISEWHENTHEDISTANCEISZERO,ITFOLLOWSFROMCONSTRAINT12THATHMBECOMESEQUALTOHINTHISWAYALLDISTANCESANDHEIGHTSAREDEFINEDFORANYGIRDERTHATBECOMESTHEUPPERMOSTSELECTEDINTERMEDIATEONEANDREESTABLISHESITSCONNECTIONTOTHEUPPERMOSTFIXEDGIRDERASTHEUPPERMOSTSELECTEDINTERMEDIATEGIRDERISCONNECTEDTOTHEUPPERMOSTFIXEDGIRDEREGGIRDER3TOGIRDER6INFIGURE3A,THELATTERSHOULDALSO,INTHESIMILARWAY,BECONNECTEDTOTHEFORMERONEGIRDER6TOGIRDER3INFIGURE3ACONSTRAINTSFORTHEUPPERMOSTFIXEDGIRDERARETHENJUSTFUNCTIONSOFTWOHEIGHTSHMANDHM1ANDADISTANCETHE1MHDPROBLEMARISESIFSOMEINTERMEDIATEGIRDERSDONOTEXIST,EGGIRDERS4AND5INFIGURE3AINSUCHCASES,HM1SHOULDNOTBECONSIDEREDINSTEAD,THEHEIGHTHSH3INFIGURE3AOFTHEUPPERSELECTEDINTERMEDIATEGIRDERSHOULDBEDEFINEDANDSUBSTITUTEDFORHM1THEVERTICALDISTANCEDHSOFTHEUPPERMOSTSELECTEDINTERMEDIATEGIRDERISTHENDEFINEDBYTHECONSTRAINT15HSMSDTHESELECTIONOFTHEHEIGHTHSAMONGALLHMCANBEPERFORMEDBYTHEFOLLOWINGLOGICALCONSTRAINTS,M2,3,M21611UPUPSMSMSHY,M2,3,M217SSSH1811UPSMSMY19SSHCONSTRAINTS16AND17SETHSTOTHEHEIGHTHMOFTHATMTHEXISTINGHORIZONTALGIRDERYM1,WHICHHASTHEEXISTINGADJOININGLOWERGIRDERYM11ANDTHEDISAPPEARINGADJOININGUPPERGIRDERYM10HOWEVER,FORM“M1THENEXTUPPERGIRDERALWAYSEXISTS,SINCEITISFIXED,IEYM1INTHISCASEWENEEDADDITIONALCONSTRAINTS,IE18AND19,WHICHSETHSTOTHEHEIGHTHM13THEMINLPOPTIMIZATIONMODELFORROLLERANDSLIDINGHYDRAULICSTEELG
- 温馨提示:
1: 本站所有资源如无特殊说明,都需要本地电脑安装OFFICE2007和PDF阅读器。图纸软件为CAD,CAXA,PROE,UG,SolidWorks等.压缩文件请下载最新的WinRAR软件解压。
2: 本站的文档不包含任何第三方提供的附件图纸等,如果需要附件,请联系上传者。文件的所有权益归上传用户所有。
3.本站RAR压缩包中若带图纸,网页内容里面会有图纸预览,若没有图纸预览就没有图纸。
4. 未经权益所有人同意不得将文件中的内容挪作商业或盈利用途。
5. 人人文库网仅提供信息存储空间,仅对用户上传内容的表现方式做保护处理,对用户上传分享的文档内容本身不做任何修改或编辑,并不能对任何下载内容负责。
6. 下载文件中如有侵权或不适当内容,请与我们联系,我们立即纠正。
7. 本站不保证下载资源的准确性、安全性和完整性, 同时也不承担用户因使用这些下载资源对自己和他人造成任何形式的伤害或损失。

人人文库网所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
 川公网安备: 51019002004831号
川公网安备: 51019002004831号