0数控龙门铣床的加工中心侧铣头结构设计说明书.doc
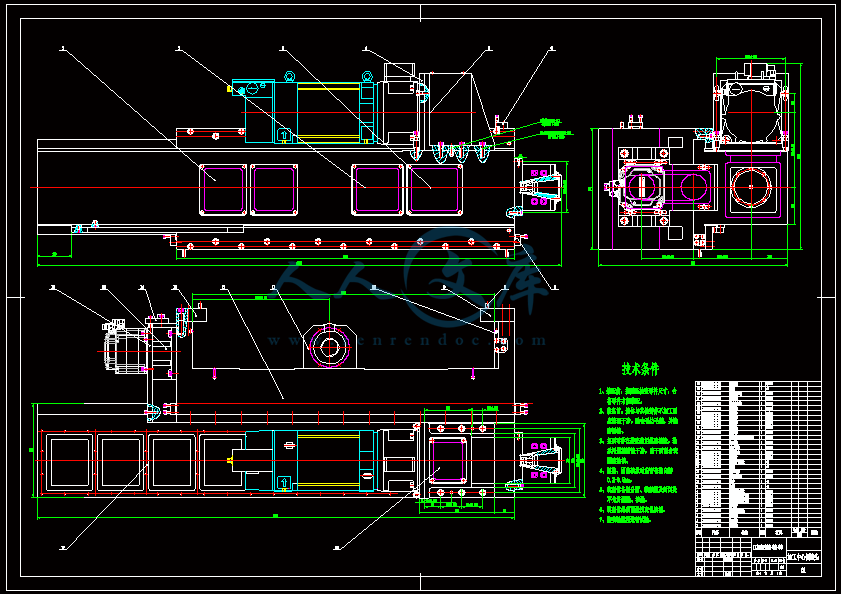
数控龙门铣床的加工中心侧铣头结构设计(含CAD图纸及仿真视频、文档说明书)
收藏
资源目录

压缩包内文档预览:(预览前20页/共85页)
编号:26848262
类型:共享资源
大小:12.11MB
格式:ZIP
上传时间:2019-11-26
上传人:机****料
认证信息
个人认证
高**(实名认证)
河南
IP属地:河南
50
积分
- 关 键 词:
-
数控
龙门
铣床
加工
中心
侧铣头
结构设计
CAD
图纸
仿真
视频
文档
说明书
- 资源描述:
-
- 内容简介:
-
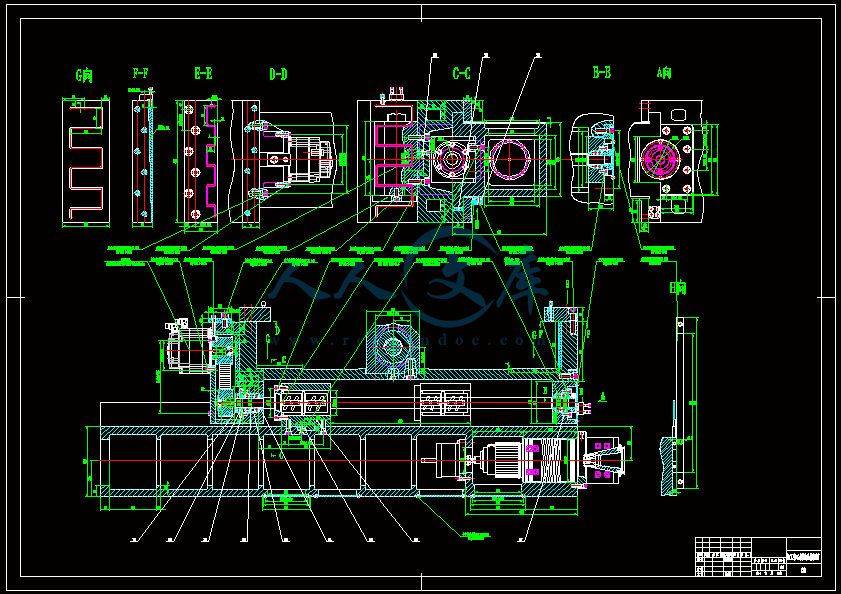
压缩包内含有CAD图纸和说明书,咨询Q 197216396 或 11970985加工中心侧铣头结构设计摘要 本设计主要是根据设计要求,依据机械设计和机械制图的基本原理对一台重型数控龙门铣床的侧铣头进行结构设计,该侧铣头能够在X 方向和Z方向两个方向上进行铣削运动。本设计主要分四部分:第一部分是根据设计要求对侧铣头的结构进行总体方案的设计,主要包括伺服进给运动和主运动方式的确定。第二部分是利用机械设计基本原理对设计中伺服进给运动和主运动系统的机械部分的设计计算,主要包括进给电动机、主轴电动机、滚珠丝杠副的选则、计算和校核以及对同步带和带轮进行设计。第三部分是根据所选择设计的主要零件,先进行大体结构设计,之后在此基础之上,利用机械制图的基本原理,应用CAXA电子图版对侧铣头的结构进行二维设计,并生成三张二维装配图纸和一张二维零件图纸。最后一部分是依据所设计的二维图,利用SOLIDWORKS软件对侧铣头结构中零件进行三维建模,并将所有建模零件进行装配,生成三维装配体;在此基础上,利用该软件做一个三维动画,显示装配体内部结构及运动方式。关键字: 重型数控龙门铣床 侧铣头 结构设计 总体方案设计 二维设计 三维建模 三维动画Structural Design of the Profile Cutter Head ofa Machining CentreAbstract: The design is mainly to design the profile cutter head structural of a heavy numerically controlled planomiller according as the rationale of mechanism design and theory of machines on the bases of design specification. The design is mainly divided into four parts:The first part is a content of total project design of the profile cutter head Structure according as design specification, including confirming the manner of servo feed motion and the main motion. The second part is design of calculations of machine parts of servo feed motion system and the main motion system according as the rationale of mechanism design. Its mainly including choose the type, the calculation and the verification of the feed electromotor, the principal axis electromotor and the ball screw, and the design of hold-in range and synchronous pulley. The third part is to design the mainly structure firstly on the bases of main parts choosed and designed in the second part, then to design two dimensional drawings, and create three assembly drawings and one detail drawings using CAXA software according to the rationale of theory of machines. The finally part is to model the parts of the profile cutter head, and create three dimensional drawings using SOLIDWORKS software according to two dimensional drawings designed in the third part;The following is to create a three-dimensional animation to show the inside structure of the three-dimensional assembly drawing and the motion manner using the software on the bases of the three-dimensional assembly drawing.Keywords: Heavy numerically controlled planomiller, The profile cutter head, Structural design, total project design, two dimensional design, three dimensional modeling,three-dimensional animation。V东北大学毕业设计(论文) 目录目 录摘 要IABSTRACT第一章 绪 论11.1 国内外数控机床的发展状况11.2 数控技术的发展趋势21.3 设计目的和意义3第二章 总体方案设计52.1设计基本要求52.2总体设计方案6第三章 伺服系统机械部分设计计算83.1滚珠丝杠副的选择计算8 3.1.1 已知参数8 3.1.2 切削力的确定83.1.3 滚珠丝扛螺母副的设计、计算83.2 进给伺服系统传动计算113.2.1 电动机选择113.2.2 同步带的设计计算173.3 机床主轴部分设计计算183.3.1 主轴电机及其减速器的选择计算183.3.2 同步带的设计计算19第四章 二维设计 214.1 大体结构设计214.2 利用 CAXA 电子图版进行二维设计22第五章 三维设计275.1 Solidworks2005软件介绍275.2 三维建模285.3 三维动画34经济技术性与环保分析35结 论36致 谢37参考文献38外文翻译39 东北大学毕业设计(论文) 第一章 绪论第一章 绪论1.1 国内外数控机床的发展状况世纪人类社会最伟大的科技成果是计算机的发明与应用,计算机及控制技术在机械制造设备中的应用是世纪内制造业发展的最重大的技术进步。自从年美国第台数控铣床问世至今已经历了个年头。数控设备包括:车、铣、加工中心、镗、磨、冲压、电加工以及各类专机,形成庞大的数控制造设备家族,每年全世界的产量有万台,产值上百亿美元。尤其是以美国和德国为代表的数控技术最为先进。只就数控铣床来说,已经出现了各式各样适应于不同加工形式的数控铣床,而只就数控龙门铣床来说,自从西班牙尼古拉斯克雷亚集团公司(Nicolas Correa,下称NC公司)80年代中期开发出第一台龙门式数控铣床,在这短短的几十年里,数控龙门铣床技术的不断发展,先后出现了各种形式的龙门铣床,到目前为止数控龙门铣床技术的发展已经相当完善。从整体上看,现在在机械行业中使用的数控龙门铣床大部分只带有立式铣头,也就是说只能对工件上表面进行Y向和X向铣削或是带有侧铣头但该侧铣头只能进行Z向进给运动。也就是说带有能够做两个方向进给运动的侧铣头还是少见的。特别是对于重型龙门铣床来说,加工工件一般都是很大很重的,移动工件时很不合理的,所以这时采用能够做两个方向进给运动的侧铣头是必要的。我国数控机床制造业在年代曾有过高速发展的阶段,许多机床厂从传统产品实现向数控化产品的转型,但数控龙门铣床并没有得到很大发展。从年“九五”以后国家从扩大内需启动机床市场,加强限制进口数控设备的审批,投资重点支持关键数控系统、设备、技术攻关,对数控设备生产起到了很大的促进作用,尤其是在年以后,国家向国防工业及关键民用工业部门投入大量技改资金,使数控设备制造市场一派繁荣,数控龙门铣床也得到了很大发展。但从年月份的上海数控机床展览会和年月北京国际机床展览会上,也看到了一些问题: (1)低技术水平的产品竞争激烈,相互之间靠压价促销; (2)高技术水平、全功能产品主要靠进口; (3)配套的高质量功能部件、数控系统附件主要靠进口; (4)应用技术水平较低,联网技术没有完全推广使用; (5)自行开发能力较差,相对有较高技术水平的产品主要靠引进图纸、合资生产或进口件组装。当今世界工业国家数控机床的拥有量反映了这个国家的经济能力和国防实力。目前我国是全世界机床拥有量最多的国家(近万台),但我们的机床数控化率仅达到左右,这与西方工业国家一般能达到的差距太大。日本不到万台的机床却有近倍于我国的制造能力。数控化率低,已有数控机床利用率、开动率低,这是发展我国世纪制造业必须首先解决的最主要问题。每年我们国产全功能数控机床台,日本年产万多台数控机床,每年我们花十几亿美元进口台数控机床,即使这样我国制造业也很难把行业中数控化率大幅度提上去。因此,国家计委、经贸委从“八五”、“九五”就提出数控化改造的方针,在“九五”期间,我协会也曾做过调研。当时提出数控化改造的设备可达万台,需投入亿资金,但得到的经济效益将是投入的倍以上。因此,这两年来承担数控化改造的企业公司大量涌现,甚至还有美国公司加入。“十五”刚刚开始,国防科工委就明确提出了在军工企业中投入亿元,用于对万台机床的数控化改造。有专家指出专家说,从整体上提高我国机床水平刻不容缓。但当前需要特别注意的是,必须快速提高数控机床产品的自主开发、制造能力。为此,要建立有效的数控技术开发中心,加强对重点工艺的研究、试验,形成成套开发能力;同时,通过国际合作生产、合资经营,实现主流产品生产的高起点、成批量、专业化。1.2 数控技术的发展趋势从目前世界上数控技术及其装备发展的趋势来看,其主要研究热点有以下几个方面:(1) 高速、高精加工技术及装备的新趋势 效率、质量是先进制造技术的主体。高速、高精加工技术可极大地提高效率,提高产品的质量和档次,缩短生产周期和提高市场竞争能力。为此日本先端技术研究会将其列为5大现代制造技术之一,国际生产工程学会(CIRP)将其确定为21世纪的中心研究方向之一。 高速加工中心进给速度可达80m/min,甚至更高,空运行速度可达100m/min左右。在加工精度方面,近10年来,普通级数控机床的加工精度已由10m提高到5m,精密级加工中心则从35m,提高到11.5m,并且超精密加工精度已开始进入纳米级(0.01m)。 在可靠性方面,国外数控装置的MTBF值已达6 000h以上,伺服系统的MTBF值达到30000h以上,表现出非常高的可靠性。 为了实现高速、高精加工,与之配套的功能部件如电主轴、直线电机得到了快速的发展,应用领域进一步扩大。 (2)5轴联动加工和复合加工机床快速发展采用5轴联动对三维曲面零件的加工,可用刀具最佳几何形状进行切削,不仅光洁度高,而且效率也大幅度提高。一般认为,1台5轴联动机床的效率可以等于2台3轴联动机床,特别是使用立方氮化硼等超硬材料铣刀进行高速铣削淬火钢零件时,5轴联动加工可比3轴联动加工发挥更高的效益。当前由于电主轴的出现,使得实现5轴联动加工的复合主轴头结构大为简化,其制造难度和成本大幅度降低,数控系统的价格差距缩小。因此促进了复合主轴头类型5轴联动机床和复合加工机床(含5面加工机床)的发展。 (3) 智能化、开放式、网络化成为当代数控系统发展的主要趋势 21世纪的数控装备将是具有一定智能化的系统,智能化的内容包括在数控系统中的各个方面:为追求加工效率和加工质量方面的智能化;为提高驱动性能及使用连接方便的智能化;简化编程、简化操作方面的智能化;还有智能诊断、智能监控方面的内容、方便系统的诊断及维修等。(4)重视新技术标准、规范的建立数控标准是制造业信息化发展的一种趋势。数控技术诞生后的50年间的信息交换都是基于ISO6983标准,即采用G,M代码描述如何(how)加工,其本质特征是面向加工过程,显然,他已越来越不能满足现代数控技术高速发展的需要。为此,国际上正在研究和制定一种新的CNC系统标准ISO14649(STEPNC),其目的是提供一种不依赖于具体系统的中性机制,能够描述产品整个生命周期内的统一数据模型,从而实现整个制造过程,乃至各个工业领域产品信息的标准化。1.3 设计目的和意义(a) 目的(1) 根据设计要求,设计一个重型数控龙门铣床的侧铣头,使其能够在横向和纵向两个方向作进给运动,对于一台重型数控龙门铣床来说通常加工的工件都是很大很重的,在加工过程中要让工件移动或是进行多次安装是很费时费力的,所以设计一个能够在横向和纵向两个方向作进给运动的侧铣头,来减少实际工件的移动和安装次数,进而减少安装的时间和由于多次安装引起的定位精度误差。(2) 使学生了解机械设备的设计过程。对作为一名将来从事机械行业的大学生来说,了解机械设备的设计过程是一个必须的。而对数控铣床侧铣头的设计完全能够体现出机械设备的设计过程以及在设计过程中应注意的问题和一般要考虑的因素。(3) 使学生能够将在大学期间所学的理论知识与具体实践相结合。当今大学生大部分都存在着不知道如何将大学所学的东西运用到实际中去,甚至认为大学所学的东西根本没有用处。(4) 使学生在实际过程中学习新的软件。通过完成这个毕业设计,以掌握当今社会上一些常用的制图软件和分析软件。现在的社会是高科技的社会,对于机械行业来说也是如此。现在的机械行业中很少有用手工绘制的图纸,而且现在的人们都有一种安全的理念和结构的美感,运用三维软件和分析软件对工程师所设计的结构进行三维建模和强度分析,可以事先发现不合理之处,以便提早加以改正。(b) 意义(1)、在现实中,带有侧铣头的数控龙门铣床是不常见的一种形式,而带有能够在两个方向上进行进给运动的侧铣头的龙门铣床更是不常见。这项设计所设计的侧铣头与其他龙门铣床部分相配合,可以应用在现实中对工件进行三个方向上的加工,从而很可能能够对工件进行一次性安装加工,这无疑可以省去很多调整时间并保证良好的安装精度。而且这是对一台重型数控龙门铣床侧铣头的设计,对于一台重型铣床来说,加工的工件一般都是很大很重的,要对工件进行多次安装是很困难的也很浪费时间,且定位精度不容易保证,而该课题所设计的侧铣头正适合这种情况,所以说这项设计有重要的现实意义。(2)、在做毕业设计的过程中学习掌握二维和三维绘图软件,为以后更好的适应社会打下良好的基础。(3)、了解机械产品的设计过程,掌握设计过程中应注意的问题和应考虑的因素。- 69 -东北大学毕业设计(论文) 第二章 总体方案设计第二章 总体方案设计2.1 设计基本要求1) 侧铣头的行程为600mm;2) 定位精度为5m ;3) 与立柱连接部分横跨度为1300mm;4) 最大进给速度为10 m/min;5) 两侧铣头中间能通过最大零件宽度为3150mm;6) 主切削力5000N。 图 2.1 加工中心方案图1图 2.2 加工中心方案图22.2 总体设计方案根据设计要求,侧铣头能够在横向和纵向进行切削进给,即在X向和Z向进行切削进给。为实现这两个运动,所以将侧铣头主要分为实现纵向运动的垂直导轨和实现横向运动的水平滑枕两部分。同时需要在这两部分上安装有实现的导轨,考虑到此数控机床是一台重型数控龙门铣床,侧铣头本身有很大的重量并且在加工过程中要受到很大的切削力的作用,这就要求所选择的导轨必须能够承受很大的重力及较高的刚度,除此之外,因为本数控机床要求有很高的加工精度,根据这一点本设计采用承载能力大结构简单刚性好的贴塑滑动式矩形导轨,在这之中之所以采用贴塑方式是因为普通的滑动导轨摩擦系数大,容易产生爬行现象,而贴塑导轨具有摩擦系数小、抗咬合磨损性能好、不易爬行、工艺性能好等优点,但是由于矩形导轨磨损后不能自动补偿间隙,这就会影响加工精度和定位精度,因此对于导轨主要承载面需要有间隙调整装置,在本设计中,采用斜镶条对其进行调整。对于主轴的运动,初步考虑了两种方案:一、采用电动机通过联轴器带动主轴运动;二、采用电动机通过同步带带动主轴运动。但是考虑到此设计是一台重型数控龙门铣床,侧铣头本身有很大的重量并且在加工过程中要受到很大的切削力的作用,要带动侧铣头运动并实现进给,这就要求选择功率很大的电动机,而这就导致电动机有很大的结构尺寸,如果采用联轴器进行连接,势必会增加侧铣头的结构尺寸,从而导致侧铣头重量的增加浪费原材料。而采用同步带传动,可以将电动机放置在侧铣头结构以外,这不但会减小侧铣头的结构尺寸,同时也大大降低了原材料的使用;除此之外,采用同步带传动,还具有传动比准确,传动效率高,噪音小的优点。这符合经济环保的要求。为保证加工精度,在这部分设计中,主轴采用高精密主轴B50-190。为了实现横向进给运动,也初步考虑了两种方案:一、采用电动机通过联轴器与滚珠丝杠螺母副连接带动水平滑枕运动;二、采用电动机通过同步带与滚珠丝杠螺母副带动水平滑枕运动。如果采用联轴器连接的方式,就要将电动机及联轴器安置在水平滑枕的尾部,而一个大功率的电动机有很大的重量,这样就会导致水平滑枕尾部承受很大的重力,从而产生很大的扭矩,这对实现水平滑枕的运动精度、定位精度产生影响,并会导致摩擦性能的降低,而且为实现设计要求,水平滑枕需要有很长的结构尺寸,如果在将电动机放置在水平滑枕尾部,这就增加了整体机床的安装空间;而采用电动机通过同步带与滚珠丝杠螺母副带动水平滑枕运动的方式,可以将电动机放置在垂直导轨上,这无疑可以减少安装空间,而且合理利用空间。之所以采用滚珠丝杠螺母副进行传动,是因为它具有摩擦损失小,传动效率高;摩擦阻力小,动静摩擦力之差极小,因而运动灵活、平稳、低速时不易产生爬行、且磨损小、精度保持性好、寿命长;丝杠螺母之间进行消隙或预紧,可以消除反向间隙、市反向无死区,定位精度高、轴向刚度大;传动具有可逆性,即能将旋转运动转换为直线运动等优点,此设计中采用的滚珠丝杠螺母副是BNFN 5020-2.5。对于主轴电动机的选择,初步选用西门子公司生产的风冷式交流感应电动机。对于伺服进给电动机,初步选用西门子公司生产的自冷式三相交流同步伺服电动机。交流伺服电动机结构简单、体积小、制造成本低;其没有电刷和换向器,不需要经常维护,没有直流伺服电动机因换向火花影响运行速度提高这种限制。为了提高水平滑枕的X方向定位精度,在该方向上安装直线光栅尺进行位置检测并构成闭环控制系统。闭环控制系统可以消除整个系统的误差,包括机械系统的传动误差等,其控制精度和动态性能都比较理想,但是系统结构复杂,安装和调试比较麻烦,成本高。东北大学毕业设计(论文) 第三章 伺服系统机械部分设计计算第三章 伺服系统机械部分设计计算3.1 滚珠丝杠副的选择计算311 已知参数丝杠的公称直径50mm,导程20mm,螺纹长度1245mm,BNFN5020-2.5。312 切削力的确定按照立铣(不对称顺铣)计算各向分力,如下图所示:已知主切削力图2.1 铣头受力示意图取 313 滚珠丝扛螺母副的设计、计算(1) 计算进给牵引力作用在滚珠丝杠上的进给牵引力主要包括切削时的走刀抗力以及移动件的重量和切削分力作用在导轨上的摩擦力。因此其数值的大小与导轨的类型有关,此处为贴塑矩形导轨,则的计算公式为: (3.1)其中,、各向切削分力,; 移动部件的重量,; 导轨上的摩擦系数,随导轨形势而不同,取0.05; 考虑颠覆力矩影响的实验系数,取1.1。(2)计算最大动负载C选用滚珠丝杠副的直径时,必须保证在一定轴向负载作用下,丝杠在回转100万转后,在它的滚道上不产生点蚀现象。这个轴向负载的最大值即称为该滚珠丝杠能承受的最大动负载C,可用下式计算: (3.2)式中:L寿命,以为一单位,丝杠转速,(r/min),用下式计算为最大切削力条件下的进给速度(m/min),可取最高进给速度的1/21/3; 丝杠导程,(mm);丝杠转速,(r/min), 为使用寿命,对于数控机床取T=15000h;运转系数,见下表。运转系数运转状态运转系数无冲击运转1.01.2一般 运 转1.21.5有冲击运转1.52.5计算: 计算结果Error! No bookmark name given.小于丝杠额定动载荷72.5KN,满足要求。(3)传动效率计算滚珠丝杠螺母副的传动效率: (3.3)式中: 摩擦角,滚珠丝杠副的滚动摩擦系数0.0030.004,摩擦角约为,即0.1667 丝杠螺旋升角 丝杠中径 = 6.8880 = = 0.976(4)刚度计算滚珠丝杠副的轴向变形会影响进给系统的定位精度及运动的平稳性,因此应考虑以下引起轴向变形的因素:丝杠的拉伸或压缩变形量:在总的变形量中占的比重较大,可以用计算方法确定。先用下式计算滚珠丝杠受工作负载的作用引起导程的变化量在计算滚珠丝杠总长度上的拉伸或压缩变形量(两端固定): (3.4)式中,在工作负载作用下引起每一导程的变化量,(mm); 工作负载,即进给牵引力,;滚珠丝杠的导程,(mm); 材料弹性模数,对钢();滚珠丝杠截面积(按内径确定)(mm2) “+”号用于拉伸,“-”号用于压缩。计算滚珠丝杠在总长度上拉伸或压缩的变形量 (3.5) 式中:滚珠丝杠在支承间的受力长度,。根据实用机床设计手册滚珠丝杠副的传动刚度主要由丝杠本身拉压刚度,丝杠副内的接触刚度,轴承和轴承座刚度,因此近似取拉压刚度的1/3(变形近似为拉压变形的3倍)。,符合要求定位精度。3.2 进给伺服系统传动计算3.2.1电动机选择 1、初选电动机和减速器(a)电动机和减速器参数电机西门子1FK7101-5AF7:额定转速3000r/min,最大输出静力矩,额定转矩,自身惯量。减速器:LP155-M01,转动惯量,。(b)转动惯量的计算丝杠导程,公称直径为50mm。 ,取工作台重量M=1000 Kg。 (3.6)其中丝杠的转动惯量: 电机轴同步带轮的转动惯量: 丝杠同步带轮的转动惯量:则:惯量匹配,符合要求。(c)电机力矩的计算 快速空载起动时所需力矩: (3.7)式中, 快速空载起动力矩,;空载起动时折算到电机轴上的加速力矩,;折算到电机轴上的摩擦力矩,; 由于丝杠预紧折算到电机轴上的附加摩擦力矩,;上式中 T时间常数摩擦力矩: 导轨摩擦力(N),空载快速起动时;传动链总效率,一般可取。附加摩擦力矩:滚珠丝杠预加载荷,一般取,为进给牵引力。滚珠丝杠导程;滚珠丝杠未预紧时的传动效率,一般取空载快速启动所需力矩:21.94Nm小于电机输出最大静转矩27Nm,电机满足使用要求。 最大切削负载时所需力矩: (3.8)折算到电机轴上的切削负载力矩,:式中:进给方向最大切削力;最大切削负载时摩擦力矩Mf,:附加摩擦力矩:最大切削负载所需力矩M切:(d)加速运行加速度 计算折算到电机轴的等效转矩 计算工作台空载加速度电机轴角加速度:2、更换电动机和减速器(a)电机和减速器参数电机西门子1FK7100-5AF7:额定转速3000r/min,最大输出静力矩,额定转矩,自身惯量。减速器:LP155-M01,转动惯量,。(b)转动惯量的计算丝杠导程,公称直径为50mm。,取,工作台重量W=1000 Kg。其中丝杠的转动惯量:则:惯量匹配,符合要求。(c)电机力矩的计算 快速空载起动时所需力矩:式中, 快速空载起动力矩,;空载起动时折算到电机轴上的加速力矩,;折算到电机轴上的摩擦力矩,; 由于丝杠预紧折算到电机轴上的附加摩擦力矩,;上式中 T时间常数摩擦力矩:导轨摩擦力(N),空载快速起动时;传动链总效率,一般可取。附加摩擦力矩:滚珠丝杠预加载荷,一般取,为进给牵引力。滚珠丝杠导程;滚珠丝杠未预紧时的传动效率,一般取空载快速启动所需力矩:17.08Nm小于电机输出最大静转矩18Nm,电机满足使用要求。(d)加速运行加速度 计算折算到电机轴的等效转矩 计算工作台空载加速度电机轴角加速度:(e)最大运行速度: ,满足设计要求。3.2.2同步带的设计计算(1) 初步选择基本参数数据带轮传动中心距224mm,同步带规格:800-8M,慈溪恒力。带轮:8-M,44齿,慈溪恒力。按照圆弧齿计算,8M型,基本参数如下:传动比,节距mm,齿形角,齿根厚s=5.15mm,齿高mm,齿根角半径mm,齿顶园半径mm,带高mm。(2) 同步带的选择计算从动带轮节径mm,外径mm,主动带轮节径mm,外径mm.初定中心距: (3.9)即 取=224mm。带的节线长度: (3.10)选择,齿数实际中心距按照可调方式: ,取224mm。(3.11)中心距调整范围:基准额定功率:带宽 (3.12) 圆弧齿带长系数,取1.00; 小带轮啮合齿数系数; 设计功率, 计算带宽:根据实际情况带宽取为45mm.作用在轴上的力:,其中:矢量相加修正系数 (3.13)33 机床主轴部分设计计算331 主轴电机及其减速器的选择计算主轴电机型号及性能参数:西门子1PH7-137 2NG-0L额定功率:28KW,额定转速2000rpm,额定转矩134Nm,最高转速10000rpm,转动惯量0.109,重量130Kg,主轴高度132mm。与1PH7-137 2NG-0L 配套的减速机型号为2LG4312, 取i=4;其性能参数为:重量62Kg。电机联接减速器,减速器连接同步带轮,带动主轴,带传动1:1主轴的转动惯量估计值:0.043 同步带轮的转动惯量估计值:材料铸钢,惯量匹配计算:不采用减速机的同步带1:1传动,0.109/(0.109+0.043+0.0295)=0.60,惯量匹配符合要求。带轮传动中心距320mm,同步带规格:1200-8M,慈溪恒力。带轮:8-YU,60齿,慈溪恒力。332 同步带的设计计算(1) 初步选择基本参数数据按照圆弧齿计算,8M型,基本参数如下:传动比,节距mm,齿形角,齿根厚s=5.15mm,齿高mm,齿根角半径,齿顶圆半径mm,带高mm。(2) 同步带的选择计算从动带轮节径mm,外径mm,主动带轮节径mm,外径mm.初定中心距: 即 取=320mm。带的节线长度:选择,齿数实际中心距按照可调方式:,取320mm。中心距调整范围:带宽取为85mm.东北大学毕业设计(论文) 第四章 二维设计第四章 二维设计41大体结构设计这部分设计是在纸面上进行的,历时一周左右。这部分工作对以后的设计工作有着重要影响,因为这部分工作关系到结构的准确性、合理性及设计的原理是否正确。所以虽然这部分的内容看起来不是很多,但是却要花费心思慎重思考和设计,稍有不慎就会对以后的设计工作产生重大影响,甚至会使以后的结构设计完全不正确,以致有进行重新设计的危险。从整体上看该侧铣头的结构主要分为竖直导轨和水平滑枕两部分。要使这两部分之间能相互运动,就是设计两个部分的连接部分,由于该侧铣头的重量比较大并且在加工过程中切削力比较大,所以就要采用承载能力较大的矩形导轨,两部分的连接部分都采用矩形导轨,为使结构固定,两导轨之间采用压板,压板安装在竖直导轨上。竖直导轨与立柱之间的导轨也通过压板进行固定,压板通过固定在竖直导轨上。由于本次设计的是侧铣头,故名思意就是可以对零件进行侧面铣削,这就要求主轴要安装在水平滑枕上,而这样主轴电机就有两个位置可以安装:一是放在水平滑枕上方,二是放在水平滑枕下方。由于所选的电机重量较大,如果放在下方,就要求连接电机和水平滑枕的部分的强度很高,而且如果发生意外会造成电机的较大损坏。所以将主轴电机放在水平滑枕上方。主轴和水平滑枕之间通过带轮箱进行结构连接。对于水平滑枕的宽度,就要考虑电机的结构尺寸,既要安置下电机,又不能有太大的空余空间,这样不但可以节省原材料而且减少安装空间。对于仅给电机的布置方式,采用将仅给电机安置在竖直导轨侧面,这样可以减小水平滑枕的扭矩,并合理利用竖直导轨侧面的多余空间,同时减少水平滑枕的横向移动空间。电机与竖直导轨之间同样通过带轮箱连接。由于将电机安装在竖直导轨上,这就要求滚珠丝杠螺母副也要安装在竖直导轨上,滚珠丝杠螺母副与水平滑枕通过丝杠螺母座连接,这样就实现了竖直导轨和水平滑枕之间的相互运动。既然丝杠螺母副安装在竖直导轨上,就要考虑丝杠与竖直导轨的连接,为实现容易安装,并实现定位,采用模块结构,将丝杠的一个滚动轴承座做成块,并采用三面定位,另一个轴承座与进给电机带轮箱做成一体,这样不安结构简单,而且容易实现进给电机与丝杠之间的中心距调整。对于该侧铣头来说,最复杂的零件莫过于水平滑枕。为实现行程的要求就要使水平滑枕的长度很长,达到2055mm,这就要考虑水平滑枕的内部结构,为了减轻重量,在保证强度的基础之上,本设计采用水平滑枕中空的结构。考虑水平滑枕与竖直导轨连接的下部导轨承受的力较大,所以在这两导轨之间加镶条进行调整。竖直导轨与立柱之间靠近主轴方向的导轨同样用镶条进行调整。对初步考虑的结构进行不断修改,最后形成比较准确的结构和尺寸,所设计的尺寸在二维图上有所体现,这里不作说明。42 利用CAXA电子图版进行二维设计(1)关于CAXA电子图版(a)软件介绍1,用户多、套数多 10万正版用户,连续七年在CAD/CAM市场销量第一,已在众多大中型企业普及应用,久经各种用户应用的考验。 2,学得快、绘图快易学易用,稍有基础者一天可学会,学习过流行CAD软件者可迅速掌握,绘图效率高。 3,图库好、标注好符合最新国标的图库,使绘图变得非常方便、快捷。工程标 注符合国标,处处体现“所见即所得”的智能化思想。4,时间省、费用省功能强大,品质卓越。以实惠的价格,即可拥有上万元软件的功能和品质。5,兼容AUTOCAD数据接口与AutoCAD进行数据交换畅通无阻。支持DWG、DXF、IGES文件读入和输出;支持WMF、HPGL图形文件的读入。读入DWG文件后能保持相同的图面效果,其线型、图层、颜色和文字风格的一致,并进行风格的编辑修改。提高对不同文字编码的处理能力,保证字符和文字读入正确,不出现乱码。读入DWG文件时,增加按颜色匹配线宽的高级选项。增加打印时按颜色设置线宽的功能,保证用户在电子图板中可以按所熟悉的AutoCAD方式处理线宽。批量转换电子图板的数据为DWG格式的数据,方便AutoCAD用户利用电子图板的数据。6,在状态栏增加显示目前执行功能的键盘输入命令提示,可帮助用户快速掌握各种键盘命令。7,CAXA电子图板是被中国工程师广泛采用的二维绘图软件,可以作为绘图和设计的平台。它易学易用、符合工程师的设计习惯,而且功能强大、兼容AutoCAD,是普及率最高的CAD软件之一。8,CAXA电子图板受用户喜爱的核心原因是电子图板能为用户解决实际问题,帮助用户提高绘图和设计的效率。所以,CAXA电子图板才能在全国各地的机械、电子、航空、船舶、教育、科研等多个行业广泛应用,其中有相当部分大中型企业、大中专院校的规模应用.(b)功能特点 1,全中文人机界面易学易用、界面友好,全中文人机界面,提供CAXA与AUTOCAD两种操作风格的界面。2,编辑与绘图强大的智能化图形绘制和编辑功能,可绘制各种复杂的工程图纸。3,动态导航定位绘制图形时系统自动捕捉中点、端点、垂足点等特征点,成倍提高您的工作效率。4,工程标注 符合国标,处处体现“所见即所得”的智能化思想,系统会自动捕捉设计意图,所有细节自动完成。5,标准图库 符合最新国标丰富的参量化国标图库,共有20多个大类,1000余种,近30000个规格的标准图符,并提供完全开放式的图库管理和定制图库手段,可方便快捷的建立、扩充自己的参数化图库。6,二维数据接口 丰富的数据接口功能,与AutoCAD进行数据交换畅通无阻。工程图输出 7,支持市场上主流的Windows驱动打印机和绘图仪,并提供了指定打印比例、拼图、排版等多种输出方式,保证您的出图效率,节省您的时间和资源。智能化的图纸管理 8,图纸管理功能按产品的装配关系建立层次清晰的产品树,自动提取相关数据,方便用户对图纸的管理、编辑和修改。并可对产品树中的信息进行查询、统计,按要求自动生成分类BOM表、装配BOM表。9,三维数据接口读入多种格式的三维数据(CatiaV4,Pro/E2001,STEP203,X_T,SAT等),提供对三维模型的浏览(旋转、放大、缩小)和测量功能。输出多种格式的三维数据。(注:该功能仅为电子图板专业版具有) 三维数据直接转为二维工程图纸10,将三维数据直接投影到二维工程图纸,提供多种视图功能,直接生成工程图绘制要求的各种视图(标准三视图、剖视图、局部放大图、方向视图等)。(注:该功能仅为电子图板专业版具有)个人管理工具XP(注:电子图板专业版附赠的独立安装产品)11,该产品主要是面向个人的文档管理系统,可以管理CAXA系列的文档及其它各类电子文档。提供文档分类存储、文档检索和浏览、版本控制、生成产品结构、汇总输出明细表的功能。(2) 二维图纸设计在这部分设计中,主要是在先前对侧铣头的大体结构的设计的基础之上,在电子图版上逐步细化设计并生成所需的二维图纸。(a)在设计前期,首先学习如何使用CAXA电子图版。在以前对CAXA电子图版有一定了解掌握的基础之上,利用一周的时间进一步熟悉CAXA电子图版各个基本命令,在这期间不对侧铣头进行详细的设计绘图,主要是画一些简单的图形来学习如何使用各个命令。从而为以后绘图打下良好的基础。(b)利用CAXA软件设计绘制二维图纸。利用CAXA软件对侧铣头整体结构设计绘制详细的二维图,这部分工作大约用时8周。在这期间逐步设计细化各个零部件的结构、尺寸、具体位置及各个零件之间连接部分的结构和配合方式。经过两个月的时间设计绘制,最后完成三张装配图、一张零件图,总计四张0号图纸。如下图所示:图4.1 二维装配图1图4.2 二维俯视图图4.3 二维前视图图4.4 二维零件图东北大学毕业设计(论文) 第五章 三维设计第五章 三维设计51 SOLIDWORKS2005软件介绍2005 软件提供了强大的绘图功能、空前的易用性,以及一系列旨在提升设计效率的新特性,推进了业界对三维设计的采用,加速了整个行业的发展步伐。 SolidWorks 2005 包括 250 多项由用户提议加入的新特性和功能改进,可以帮助机械设计师、模具设计师、消费品设计师,以及其他专业人员更快、更准确、更有效率地将创新思想转变为市场产品。由于这些改进, SolidWorks 2005 已成为市场上扩展性最佳的软件产品,也是惟一集 3D 设计、分析、产品数据管理、多用户协作、以及注塑件确认等功能的单一软件。它的主要改进包括: (1)机械设计 最大的改进是加入了一个扩展库,包含数百个预先设计好的常用元件,包括阀门、密封槽、密封圈,符合 SAE (汽车工程师协会)标准的各类槽,用户自己创建的元件, 2D 标注和功能块,来自 SolidWorks 3D Content Central 服务库的零部件,以及其他符合权威机械手册标准的零部件。新的焊接功能可以自动生成切割清单、定义坡槽。 (2) 模具设计 SolidWorks 2005 纳入了 MoldflowXpress。SolidWorks 2005 还为模具设计提供了一个侧凸模功能,可以在每个面自动创建侧凸模,以方便将注塑完成的零件从模具中取出。 (3)消费品设计 SolidWorks 2005引入了高端消费品的设计功能。这些新功能使相邻部件、圆角、以及其他可弯曲、扭转、拉伸元件的设计实现了自动化。 (4)为所有用户增强的功能 SolidWorks 2005 引入了大量易用、高效的系统管理功能,适用于 3D 机械设计所涉的不同行业。 1)系统增强 在 SolidWorks 2005 用户界面上有一个新的 TaskPane 窗口,集中了所有文件、文件夹和相关内容。另一个有用的升级是专利技术“ SelectOther ”,它能够迅速剖开元件表面,显示出内部的零件。 2)系统管理 SolidWorks 2005 中包含了一系列旨在简化管理和增强性能的改进。软件的新功能之一用来实现对新增软件和软件更新的中心管理,能够充分节省管理者的时间,并确保用户使用到最新版本。 SolidWorks 2005 还包含一个 SolidWorks Rx。SolidWorks 2005 还首次允许用户在不联网情况下借用网络使用权。 3)数据管理 PDMWorks 产品数据管理软件被内置到了 SolidWorks Office Professional 中。 4)集成分析 一个新的“ Displacement Value ”工具被加入到 COSMOSXpres 中。 52 三维建模在二维设计完成的基础之上,参考二维设计图纸的零件尺寸,利用SOLIDWORKS软件多个零件进行三维建模,这部分设计历时2周,即半个月时间,共建模零件40个,装配体1个,在这其中,对零件建模和装配体进行多次修改,最后生成最后成品。下面列出了几张装配体样图及几个建模零件样图:图 5.1 侧铣头三维装配图1图 5.2 侧铣头三维装配图2图5.3 侧铣头三维装配图3图5.4 水平滑枕图 5.5 主轴 图5.7 主轴电机 图5.6 主轴电机带轮箱图5.8 进给电机带轮箱 图5.9 主运动带轮中心距调整板 图5.10 竖直导轨丝杠螺母座 图5.11 主轴电机带轮 图5.12 伺服进给同步带中心距调整盖板 图 5.13 镶条调整座 图 5.14 丝杠 图 5.15 丝杠螺母 图 5.16 进给电机带轮 图 5.17 进给丝杠带轮 图 5.18 水平滑枕丝杠螺母座 图 5.19 液压缸 图 5.20 进给电机 图5.21 轴承 图 5.22 轴承座5.3 三维动画为了更清晰直观地反映侧铣头内部结构及运动过程,所以在设计即将结束时,特意为装配体制作了一个简单的三维动画;这部分设计工作历时两天,在制作中主要是应用了SOLIDWORKS软件三维动画制作插件中生成爆炸试图及动画向导等简单命令。.三维图侧铣头装配图(爆炸).avi 。图5.23 爆炸图东北大学毕业设计(论文) 经济技术性与环保分析经济技术性与环保分析如今的工业生产非常注重工作效率和经济效益,因此对产品设计做出适当的经济和技术分析是非常重要的。在经济性这方面,本设计完全符合这方面特点。在整体结构的设计上,我们在满足强度要求和技术要求的基础上,设计了最小的结构尺寸,使用了最少的原材料,这是经济性表现最为突出的一方面;除此之外,在整体结构的设计中,大部分结构都是比较简单的结构形式,这样也减少了加工过程中的工作量;同时在设计中,认真分析计算,从而得出比较准确的数据,这样在各个部件的选择上就有了很大的优势,避免了不必要的资金浪费。例如对滚珠丝杠的选择,选择了传动精度很高,而且价格适中的BNFN5020-2.5;以及对两个电动机选择也是经过认真分析计算,从而选择即满足传动的动力要求,又没有出现“大马拉小车”的现象,这无疑也节省了一部分资金。在技术性方面,本设计最突出的一个特点就是,在实现横向移动时,另加了一个直线光栅尺进行位置检测,这样构成一个闭环系统,这样的结构在定位精度上更具有优势。现代的产品设计都会注意环保问题,因为环境的可持续性发展成为一个战略性的问题已经摆在人们面前,在产品的设计中一定要考虑到对于环境的影响,并应把对环境的损害降到最低点,特别是在机械产品设计中更应注意这个问题,因在机械产品中,都要对其进行润滑,这样势必会对环境有一定影响,这就要求在设计中充分考虑润滑油等循环问题。在本设计中,充分考虑了这一要求,在各个需要润滑的表面都加工了油路,并注意了油路的配合,避免了润滑油的渗透。 东北大学毕业设计(论文) 结论结 论本次毕业设计的任务是对一台重型数控龙门铣床的侧铣头结构进行设计,具有一定的现实意义。在本设计中,为实现两个方向上的运动,将侧铣头主要分为垂直导轨和水平滑枕两部分,导轨采用贴塑滑动式矩形导轨;在伺服进给系统中,使用西门子公司生产的交流同步伺服电机通过同步带连接滚珠丝杠螺母副带动水平滑轨运动实现X向进给。在主运动系统使用西门子交流感应电动机通过同步带带动高精密主轴转动实现主运动。同步带传动都是采用1:1传动。但是本设计中只进行了结构设计,没有考虑侧铣头的控制部分和润滑油的循环机构,希望以后能设计一个与之配合的电器控制部分和油路循环机构。通过这次毕业设计,不仅对机械的基础知识和机械结构有了更深的理解,而且也实现了自己对大学四年所学到的知识的一个系统的复习。在设计过程当中,逐步了解了机械产品的一般设计过程以及在设计过程中应该注意的问题和应考虑的因素,并且对CAXA电子图版和SOLIDWORKS软件更加熟悉。毕业设计虽然结束了,大学四年的学习生活也即将结束,但这只是人生的一个新的开始。我的知识,特别是在机械专业方面的知识还刚刚是打下了一个良好的基础,学无止境,还有很多问题需要我去研究,去探索。因此,在以后的工作和学习生活中,我将继续努力学习积累更宝贵的专业知识,争取做到最好。东北大学毕业设计(论文) 致谢致 谢本次毕业设计历时三个半月,在此过程中,我特别要感谢的是指导我毕业设计的张耀满老师。在设计过程中,从开始设计计算一直到提交毕业论文,都得到了张老师悉心的指导。在这几个月的时间里,张老师严谨的治学态度、一丝不苟的工作作风和谦和的待人态度都对我产生了深深的影响,这些将激励我在以后的学习工作中更加努力。在张老师悉心的指导下,我圆满地完成了此次毕业设计。值此毕业设计即将结束之际,学生在此谨向导师表示由衷的感谢、崇高的敬意和真心的祝福:祝福尊敬的张老师:工作顺利,身体健康,万事如意! 同时感谢在我毕业设计完成之际,为我审图的刘平老师,值此成文之际也向您表示由衷的感谢!在设计过程中,我也得到了同组同学的帮助,在此我也向他们表示深深的谢意和由衷祝福:祝福他们在以后的学习生活中笑口常开!感谢所有帮助过我的老师和同学!东北大学毕业设计(论文) 参考文献参考文献1、 徐炳松,张秀艳,张茵麦.画法几何及机械制图M。高等教育出版社,1999.2、 数控技术和装备发展趋势及对策J. 机械设备新闻资讯网.2005-08-07.3、 龙门铣的先驱者来到中国J. 96航空翩遗技术,2005年第8期 .4、 国内外数控技术发展状况J. 中国自动化网,2005-9-28 .5、 专家指出要加大我国数控机床研发力度J. 新华社,2003-7-2.6、 机床设计手册3M. 机械工业出版社, 1986.7、 机床设计图册M. 上海科学技术出版社, 1979. 8、巩云鹏,田万禄,张祖立等.机械设计课程设计M.东北大学出版社,2000.9、张玉,刘平.几何量公差与测量技术M.东北大学出版社。1999.10、喻子建,张磊,邵伟平.机械设计习题与解题分析M.东北大学出版社.2000.11、阎保民, 鲍绍箕. XKB2320A型数控龙门铣床动态特性的试验研究J. 大连理工大学学报, 1983年03期.12、孙振功. 数控龙门铣床的研制J. 水利部电力工业部机电研究所 13、王启义.机械制造装备设计M。冶金工业出版社,200214、孙智礼,冷兴聚,魏延刚等.机械设计M.沈阳:东北大学出版社,2000.15、David Murray著,刘长征译.精通Solidworks 2003M.清华大学出版社.2004. 16、王仁德,张耀满,赵春雨.机床数控技术M。沈阳:东北大学出版社,2002. 17、机械设计手册(软件版)R2.0. 机械工业出版社.18、Visualization Process for Design and Manufacturing of End MillsJ .Sung-Lim Ko, Trung-Thanh Pham, Yong-Hyun Kim Springer Berlin / Heidelberg.19、Interference-free tool-path planning for flank milling of twisted ruled surfacesJ .Jung-Jae Lee, Suk-Hwan Suh .Springer London ,Volume 14, Number 11. 东北大学毕业设计(论文) 外文翻译An assessment of quasi-static and operational Errors In NC machine toolsChatterjee, S.Journal of Manufacturing Systems.Dearborn: 1997.Vol.16,Iss.1;pg.59,10pgsAbstract This paper reports the results of a comparative study of predictive error modeling and machining-cycle machine tool accuracy. The total positional error due to geometric accuracy errors was modeled for a particular type of NC machine tool. Subsequently, the NC machine tool was tested for geometric accuracy for repeatability, small-load hysteresis, linear displacement accuracy, straightness, roll, pitch, yaw, and spindle drift. The measurements were then used as input parameters in the error model to predict the total resulting error. Machining was performed next on an aluminum workpiece, and a set of sensors was used for on-line force, torque, and temperature data acquisition. The finished workpiece was post-process inspected for all dimensions on a coordinate measuring machine. An analysis of data from the model, post-process measurements, and static geometric accuracy machine tool characterization parameters indicates significant shifts in machine performance under actual cutting conditions. Based on the findings, some important research issues are presented. Keywords: Machine Tool Characterization, Thermal Errors, Quasi-Static Errors, Machine Tool Error Prediction Introduction The accuracy of a numerically controlled machine tool depends on the initial machine tool conditions, the operating conditions, and the interaction of individual members of the machine tool at those conditions. This net effect manifests as part accuracy in manufacturing. Machine tools may also exhibit deviations in measured characteristics between static and operating conditions. It is important to determine the magnitudes and trends of such deviations for error correction purposes. This paper reports the results of a comparative study of predictive error modeling and machiningcycle machine tool accuracy. The positional errors due to geometric accuracy errors were modeled for a particular type of NC machine tool. The motivation of this study was to examine deviations between error prediction approaches and actual part errors under fixed machining load cycles for a given machine tool structure. Based on the theoretical formulation of errors in Cartesian directions and geometric accuracy measurements, the total error in each Cartesian direction was determined as a function of machine tool position. The actual errors from a machining cycle were then determined from postprocess inspection. The findings indicated significant deviations in machine tool performance between static and operating conditions. The next section of the paper surveys literature in this field and is followed by theoretical formulation and experimental setup descriptions. Presentation and discussion of results of errors from the theoretical model and the machining tests are followed by a discussion of future research issues and conclusions. Literature Survey The literature survey discusses (1) quasi-static characterization and modeling studies of machine tool and experimental work and (2) the modeling of thermal effects in machining. Quasi-static machine tool accuracy studies have been performed by researchers to characterize and model machine tool errors under static conditions. Techniques for the automatic compensation of alignment errors and volumetric accuracy modeling of machine tool positioning have been reported. Mou and Lius used kinematics in modeling machine tool errors for compensation. Dorndorf, Kiridena, and Ferreira9 followed error budgeting and cost minimization to determine quasi-static error components of machine tool errors. Shin, Chin, and Brink0 proposed seven procedures for the characterization of CNC machine tools. These include the volumetric accuracy tests that measure the 21 quasi-static error components, the warm-up test, power transmission efficiency estimation, cutting performance test, cutting accuracy test, spindle dynamic compliance measurement, and spindle out-of-roundness measurement. The thermal effect of machining on part tolerances is a well-recognized problem.ll,2 Researchers have attempted to model the thermal effects analytically and empiricallyl3-IS for purposes of control and compensation. Fraser, Attia, and Osman6,1 pointed to deficiencies of implementing real-time thermal control systems arising from measurement problems during actual cutting, slow response time of thermal deformation prediction models, and use of empirical models with constants that are calibrated based on off-line idle running conditions. They reported the development of a generalized modeling of thermal deformation of machine tool structures that combines mathematical modeling with empirical calibration. Fraser, Attia, and Osman claim significant accuracy and computational efficiency of their model based on finite element simulations. Adaptive error correction for thermal errors based on process-intermittent and post-process part measurement has also been attempted by Mou, Donmez, and Cetinkunt.18,199 They modeled geometric-thermal and residual error for a two-axis turning center as a function of position, and pre-process characterization parameters of the machine tool, such as roll, pitch, yaw, linear displacement accuracy, parallelism, and orthogonality errors. Mou, Donmez, and Cetinkunt also used regression techniques in error compensation; however, the results of their study reveal that adaptive compensation through geometric-thermal and residual error modeling is unable to explain deviations between part specification and post-process measurement. From the literature survey, it is evident that research in machine tool thermal control has progressed in quasi-static error modeling and experimental error control. The relevance of using static machine tool characterization parameters for process characterization and control is an important issue.2 Also important is the relevance of the sole use of quasi-static error predicting models for compensation purposes because machine tools can exhibit performance variations depending on the load cycle. In other words, the question arises of the usefulness of quasi-static measurements for estimating process errors and process control because machine parameters are likely to vary with cutting loads due to heat load variations. It is necessary to examine the magnitude of differences between noload, load cycle condition measurements, and model-predicted errors for accurate compensation. As stated before, this study examined the variation between predictive error modeling and machining-cycle machine tool accuracy for fixed cutting load cycles. The next section presents the theoretical model for determining the error at a point. Theoretical Formulation In this section, the quasi-static error model is derived for the machine tool used. The equations below relate the total quasi-static error contribution for the 21 measured error parameters. The machine tool shown in Figure 1 was of the XYFZ Ref. 4) type, where F represents the machine frame, Z represents the motion of the tool in the Z direction with respect to F, and X and Y represent motion directions of the workpiece with respect to F. For this type of a machine tool, table motions in the X and Y directions move the workpiece, causing translational and rotational errors of a point P on the workpiece. For motions in the Z direction (motion of the tool), translational errors of the Z axis and rotational error of the tool axis with respect to the frame are to be considered.Enlarge 200%Enlarge 400%Figure 1Schematic of Machine Tool and Sensor ArrangementEnlarge 200%Enlarge 400%Enlarge 200%Enlarge 400%In Figure 2, P represents a point on the workpiece that moves with the table in the X and Y directions. The point O represents the origin of the frame of the machine and is the frame of reference. The point P is located by the tool via Z-direction motion. Let O Oz, 03, and WO represent the origins of the X, Y, Z directions and the workpiece, respectively. As the table moves in the X, Y, and Z directions, the origins 1, 02, and 03 translate and rotate (shown in Figure 2 for 01 and Oz translated and rotated). For table motions in the X and Y directions, the position of the point P can be represented as The rotation matrices (matrices describing the infinitesimal rotation of one axis for motion along another), the X, Y, and Z matrices, and the tool offset vectors are given below. Here, su (V) is the rotation about the U axis under V-axis motion and is counterclockwise positive. 8U(V) is the translation error associated with the U direction for the V direction of motion. U and V may be replaced by X, Y, and Z. The out-of-squareness of Y with X, Z with Y, and Z with X are represented as ay, azy, and azx, respectively. The T matrix represents the tool offsets in X, Y, and Z, respectively. The position of a point and the total error can therefore be determined by the substitution of the matrices above in Eq. (1) as given below. To do this, all 21 geometric accuracy error parameters associated with the translation, rotation, and straightness errors and tool offset values have to be measured. These values can then be inserted into the equations for X, Y, and Z positions shown below, and the positioning errors in the X, Y, and Z directions (the difference between Xp and X, Yp and Y, and Zp and Z) can be computed from the terms on the right-hand side of the respective equations.Enlarge 200%Enlarge 400%The position of a point P can be determined by substituting programmed coordinates (XY,Z) and measured geometric accuracy parameters in the equations below. The net error can then be determined as the difference (between Xp and X, Yp and Y, and Zp and Z) computed from the terms on the right-hand side of the respective equations given below. The components of the equations above involve coordinate points (X, Z) and errors due to position, rotation, and squareness of the machine tool. To determine the errors due to quasi-static effects, it is necessary to determine experimentally the 21 error parameters and use them in the equations above. Once these errors are known, they can be compared with post-process inspection of a machined workpiece. The next section describes the experimental setup for the geometric accuracy measurements, machining tests, and post-process inspection procedures. Experimental Setup The experimental details discussed here include a description of (1) temperature sensor instrumentation, (2) static machine tool characterization, (3) workpiece design and cutting cycle parameters, and (4) inspection procedures. Enlarge 200%Enlarge 400%Figure 2Origin Displacements and Rotations for Table TravelIn this investigation, a three-axis numerically controlled milling machine was instrumented for measurement of temperatures and for cutting forces and torques. A total of 19 thermocouples were used to measure the temperature of the machine tool structure at all times. Figure 1 shows the schematic of the machine tool and the sensor placement. Table 1 lists the thermocouples for their numbered locations shown in Figure 1. The thermocouples were calibrated prior to experimentation, and their locations were based on experiential judgment. For static characterization, the 21 error parameters (six error terms for each axis: positioning error along axis of motion, straightness errors along the two other axes for this motion, pitch, roll, yaw, and the straightness errors among the three axes) were determined. A laser interferometer, an electronic level, and an autocollimator were used to measure the positioning errors and roll, pitch, and yaw errors of the axes, respectively. Additional static characterization tests included a repeatability test, a machine hysteresis test for small-load deflection, and spindle drift tests under no load, 524 rpm, and 4000 rpm. All characterization tests were in accordance with the ANSI B5.54 machine tool performance evaluation standard.20 The cutting tests were performed on a flat aluminum pre-machined, bottom-lapped workpiece mounted on a carrier plate according to ANSI B5.54. The machining pattern consisted of face milling the top surface, end milling a step on the periphery of the workpiece, milling two circular pockets in the center of the test piece, and plunge milling, boring, and counterboring a series of 36 holes. All tools were of HSS. The schematic of the tool path is shown in Figure 3, and the cutting tools and machining parameters are presented in Table 2. The dynamometer and temperature sensors were interfaced through data collection software to a PC for on-line collection and storage of data. The finished part was inspected to specifications using a coordinate measuring machine. The repeatability and straightness along the X and Y axes were calculated. The deviation of the bore and counterbore axis with respect to the nominal were also calculated based on measurements. The temperature of the part was allowed to stabilize before inspection. The feed values of 4 ipm and 5 ipm for tool 2 were for the initial machining for 36 bores and counterbores. For tool 3, a feed of 8 ipm was used for circular interpolation of the 3.74, 2.52, and 2.007 center pockets. The other feed values of 4 ipm and 5 ipm in tools 3, 4, and 5 were used in plunge cuts for the center pockets (tool 3) and in finish boring and counterboring the holes (tools 4 and 5) to depths specified. The room temperature was monitored and the variation maintained within 1 oC. Results and Discussion In this section, modeled results are compared with actual errors, dynamic and quasi-static repeatability variations are noted, and machine tool structural temperature variations are shown. Predicted vs. Actual Error Figures 4 and 5 compare the actual and modeled errors in the X and Y directions for the 36 bore and counterbore centers. The known nominal positions of the centers of the bores and counterbores and static characterization parameters were used in Eq. (3) to calculate the errors in the centers in the workpiece coordinate system. Enlarge 200%Enlarge 400%Table 1Thermocouple LocationsEnlarge 200%Enlarge 400%Figure 3 Finished Workpiece Specifications and Tool PathEnlarge 200%Enlarge 400%Table 2 Standard Tools and Machining Parameters Enlarge 200%Enlarge 400%Figure 4 Predicted vs. Actual Errors for the X Direction Enlarge 200%Enlarge 400%Figure SPredicted vs. Actual Errors for the Y DirectionThe model error shows that the combined effect of all static errors is to overposition a point during machining operations with respect to its origin. This can be explained from Figures 6 and 7, which show the linear displacement accuracies for the X and Y direction motions. It is evident that the table fails to reach (underpositions with respect to a fixed reference point) the programmed point for its entire travel. Thus, when the table is moved along the X and Y axes and the tool is subsequently lowered for machining, the point will be overpositioned with respect to the workpiece origin. The actual bore and counterbore deviations are also seen to vary with hole positions and are not correlated with the modeled error. The profile of these deviations suggests changes in machine operational characteristics from the static ones and also seems to indicate dependency on the specifics of the process, that is, the operational sequence and parameters. Also, changes in the thermal load conditions may have a role. The thermal profile for this machine tool was measured and is discussed later. Repeatability Analysis Figure 8 shows the repeatability along the X and Y axes. The repeatability along an axis is measured as the difference between bore and counterbore coordinates for that axis. For example, for hole 1, the repeatability along the X axis is (measured X-axis bore dimension minus measured X-axis counterbore dimension). The repeatabilities for all other hole centers have been determined along both the X and Y axes. The repeatability along both the axes is found to vary with hole position with a maximum repeatability error of 0.0011 along the X axis and 0.0008 along the Y axis. These values are over a length of 11.5 along the X direction and 5.2 along the Y direction (see Figure 8). The values can be compared with quasi-static repeatabilities of 0.000091 and 0.00004 along the X (20) and Y (10) axes, respectively, in Figure 9. The magnitude as well as the position of occurrence is different for both cases. It is clear that no-load condition repeatability is significantly different from cutting-load repeatability. is evident in the work of Mou, Donmez, and Cetinkunt89 where modeling and compensation for geometric-thermal related error was unable to account for process-related errors. The processrelated errors depend on tool deflection, machine tool distortion and part temperature variations due to thermal load, material properties, tool wear, coolant effects, and environment effects. The temperature variations in parts of the machine tool structure and coolant inlet and outlet have been shown here to be significant to cause overall positional variations. Enlarge 200%Enlarge 400%Figure 6 Linear Displacement Accuracy for the X Axis Enlarge 200%Enlarge 400%Figure 7 Linear Displacement Accuracy for the Y Axis Enlarge 200%Enlarge 400%Figure 8 Dynamic Repeatability Measurements Enlarge 200%Enlarge 400%Figure 9 Quasi-Static Repeatability Measurements Enlarge 200%Enlarge 400%Figure 10 Temperature Variations of the Spindle Bearings Enlarge 200%Enlarge 400%Figure 11 Temperature Variations Along Machine Frame Enlarge 200%Enlarge 400%Figure 12 Temperature Variations in Coolant It is evident from the results that significant variations exist between static and operational machine tool characterization parameters and model-based error prediction. These parameters are likely dependent on cutting conditions. Such dependencies, although mentioned in the past, have not been investigated. They are extremely important in machine tool characterization under operating conditions from a machine tool design, purchase, and usage perspective. This implies that qualification and compensation of a machine tool by quasi-static measurement and modeling may not be suitable for process error reduction. For example, for this machine tool, quasi-static and load condition repeatability for the X axis were 0.000091 and 0.0011, respectively. This is more than an order of magnitude difference and establishes that pre-process machine tool characterization may not be enough for error correction and control purposes even if performed under varying temperature conditions because of the absence of heat loads induced under actual cutting conditions. It is important to view machine tool characterization from a perspective of application load cycles, which are due to different work and tool materials, feeds, speeds, depths of cut, and features being generated. All of these are likely to produce different heat loads, resulting in variations in parameters. Static characterizations actually are under best conditions; for machine tool characterization to be meaningful, cutting condition characterizations are important. This is evident from the data presented. However, a load cycle based characterization is extremely difficult and time consuming in reality because of many different combinations of work and tool materials, speeds, feeds, depths of cut, and workpiece features. Also, reliable real-time measurement of relative displacement between the tool and workpiece is extremely difficult, if not impossible, due to the machining environment. A fair assessment of a load cycle is from on-line process outputs, such as forces, torques, and temperatures. Thus, one alternative approach may be to construct models for estimating errors by separating process errors due to deflection and vibration from on-line force and torque sensors and measurement of tool wear. This approach is currently being examined by the authors. Some pertinent research issues are presented as follows: Apportioning thermal error magnitudes by considering deflection and wear of cutting tools, thermal deflection of the structure for specific cutting conditions. Machine performance testing in machining a wide array of features under different cutting conditions and for different materials. Modeling machine tool accuracy parameters as a function of load conditions. Developing a knowledge-based control system for predicting and controlling thermal errors from past knowledge. Conclusions This research investigated variations between predictive error modeling and machining-cycle machine tool accuracy. An instrumented machine tool was quasi-statically characterized and used for machining features on an aluminum workpiece. Post-process inspection and data analysis indicated that error compensation based on static measurements may not be sufficient. Based on the findings, some important research issues have been presented. Acknowledgments The author acknowledges Martin-Lockheed Energy Systems for permitting the use of the Y-12 facilities at Oak Ridge, TN, during the course of this study. The assistance of various personnel at the Oak Ridge Center for Manufacturing Technology at Y- 12 in machine tool operation, instrumentation, and data collection is also gratefully acknowledged. Reference1. D.L. Leete, Automatic Compensation of Alignment Errors in Machine Tools, International Journal of Machine Tool Design and Research (vl, 1961), pp293-324. 2. R. Schultschik, The Components of Volumetric Accuracy, Annals of CIRP (v25, nl, 1977), pp223-227. 3. R. Hocken, J.A. Simpson, B. Borchardt, J. Lazar, C. Reeve, and P. Stein, Three Dimensional Metrology, Annals of CIRP (v26, n2, 1977), mr)403-408. 4. G. Zhang, R. Ouyang, B. Lu, R. Hocken, R. Veale, and A. Donmez, A Displacement Method of Machine Geometry Calibration, Annals of CIRP (v37, nl, 1988), pp515-518. 5. PM. Ferreira and C.R. Liu, A Contribution to the Analysis and Compensation of the Geometric Error of a Machining Center, Annals of CIRP (v35, nl, 1986), pp259-262. 6. PM. Ferreira and C.R. Liu, An Analytical Quadratic Model for the Geometric Error of a Machine Tool, Journal of Manufacturing Systems (v5, nl, 1986), pp51-62. 7. PM. Ferreira and C.R. Liu, A Method of Estimating and Compensating Quasistatic Errors of Machine Tools, Journal of Engineering for Industry (vi 15, Feb. 1993), pp149-159. 8. J. Mou and C.R. Liu, A Method for Enhancing the Accuracy of CNC Machine Tools for On-Machine Inspection, Journal of Manufacturing Systems (vl, n4, 1992), pp229-237. 9. U. Dorndorf, VS.B. Kiridena, and PM. Ferreira, Optimal Budgeting of Quasistatic Machine Tool Errors, Journal of Engineering for Industry (vl 16, Feb. 1994), pp42-53. 10. YC. Shin, H. Chin, and M.J. Brink, Characterization of CNC Machining Centers, Journal of Manufacturing Systems (v10, n5,1991), pp407-421. 11. R.J. Hocken, Technology of Machine Tools, Machine Tools, Machine Tool Task Force, Volume 5-Machine Tool Accuracy (Berkeley, CA: Lawrence Livermore Laboratory, 1980). 12. J.B. Bryan, International Status of Thermal Error Research, Annals of CIRP (v39, n2, 1990), pp645-656. 13. J. Jedrzejewski, J. Kaczmarek, Z. Kowal, and Z. Winiarski, Numerical Optimization of Thermal Behavior of Machine Tools, Annals of CIRP (v39, nl, 1990), pp379-382. 14. R. Venugopal and M.M. Barash, Thermal Effects on the Accuracy of Numerically Controlled Machine Tools, Annals of CIRP (v35, nl, 1986), pp255-258. 15. M.H. Attia and L. Kops, A New Method for Determining the Thermal Contact Resistance at Machine Tool Joints, Annals of CIRP (v301, 1981), pp259-264. 16. S. Fraser, M.H. Attia, and M.O.M. Osman, Modelling, Identification and Control of Thermal Deformation of Machine Tool Structures: Part IConcept of Generalized Modelling, Proceedings of the ASME Winter Annual Meeting (PED v68-2, 1994), pp931-944. 17. S. Fraser, M.H. Attia, and M.O.M. Osman, Modelling, Identification and Control of Thermal Deformation of Machine Tool Structures: Part IIGeneralized Transfer Functions, Proceedings of the ASME Winter Annual Meeting (PED v68-2, 1994), pp945-953. 18. J. Mou, M.A. Donmez, and S. Cetinkunt, An Adaptive Error Correction Method Using Feature-Based Analysis Techniques for Machine Performance Improvement: Part I-Theory Derivation, Proceedings of the ASME Winter Annual Meeting (PED v68-2, 1994), pp909-917. 19. J. Mou, M.A. Donmez, and S. Cetinkunt, An Adaptive Error Correction Method Using Feature-Based Analysis Techniques for Machine Performance Improvement: Part II-Experimental Verification, Proceedings of the ASME Winter Annual Meeting (PED v68-2, 1994), pp919-929. 20. Methods for Performance Evaluation of Computer Numerically Controlled Machining Centers, ANSI Standard B5.54 (1992). 21. M. Weck, Static and Pseudostatic Deformations, in Technology of Machine Tools, Machine Tool Task Force, Volume 5-Machine Tool Accuracy (Berkeley, CA: Lawrence Livermore Laboratory, 1980). 数控机床准静态和操作误差的评定chatterjee,S . 制造协会期刊。日期:1997年,Vol.16, lss; pg 59, 10pgs摘 要 这篇文章介绍了预测误差建模和加工循环机床精度的比较研究的结果。取决于几何精度误差的总位置误差作为数控机床的一种特殊形式被建模。接着,对该数控机床的几何精度进行了测试,这些几何精度包括重复性、小负荷滞后性、直线位移精度、直线度、滚动、螺距、偏角以及心轴滑移等。而后,这种测试结果被用作误差模型的输入参数,该误差模型是用于预测总结果误差。接下来是加工一个铝制工件和用一系列传感器在线测量力、力矩以及温度数据。最后工序是在一台并行的测量设备上对成型工件所有尺寸进行检测。从对该模型、末道工序的测量结果以及静态几何精度机床特性参数的分析都表明在实际切削状态下加工过程的重要变化。基于这些发现,一些重要的调查问题呈现在我们面前。关键词:机床特性、与温度相关误差、准静态误差、机床误差预测说 明一台数控机床的精度取决于原机床的工作环境、操作环境及在这些环境中机床各部件之间的相互影响。这个系统作用在制造中也影响零件精度。机床的静态特性和动态特性之间也存在着偏差。对于误差校正值的作用来说,确定该偏差的大小和趋势是很重要的。这篇文章介绍了预测误差建模和加工循环机床精度的比较研究的结果。取决于几何精度误差的总位置误差作为数控机床的一种特殊形式被建模。这项研究的目的是测试在一个给定的机床机构在负载循环中预测误差和零件实际误差之间的偏差。基于在迪卡尔误差理论和几何精度测试方法,迪卡尔范围内的总误差是由机床位置函数决定的。来自加工循环的实际误差是由末道检测工序决定的。这些发现表明机床在静态和动态环境下运转存在很大偏差。这篇文章的下一部分在该领域对样机进行研究并且有理论公式和实验过程描述。在对理论模型和加工测试的误差结果说明和讨论之后将是一个问题研究前景的讨论和结论。调 研这项调研讨论了准静态特征、机床建模研究、试验工作及加工过程中样机与温度相关的影响。准静态机床精度研究已经被研究者用于在静态环境中表示和构造机床误差模型。对于校正误差的自动补偿技术和机床位置的垂直精度建模已经有相关报道。摩尔和李文斯在机床误差建模中应用运动学补偿技术。Dorndorf, Kiridena, and Ferreira9用误差预算和成本最小化来决定机床误差的准静态误差组成。Shin, Chin, and Brink0将7程序视为CNC机床的特征。这些包含volumetric精度测试,这种测试包括21个准静态误差组成部分测量、温升测试、动力传动效率的估计、切削测试、切削精度测试、心轴动态可塑性测试及心轴同轴度测试。加工中与温度相关的影响对零件公差的影响是个很容易认识的问题。2名研究人员已经尝试着根据分析和经验对温度相关的影响进行建模已达到控制和补偿的目的。Fraser, Attia, and Osman6,1指出了实现实时温度相关控制系统的不足是来自在实际切削中测量问题、延迟预测模型热变形的时间响应以及带有在基于空转环境下被校准的恒量的经验模型的利用。他们声称机床结构热变形建模的发展将于数学建模和经验标准相结合。Fraser, Attia, and Osman声称他们基于有限元仿真的模型的有效性和计算效率。Mou, Donmez, and Cetinkunt.18,199也已经尝试着对给予工序间断和工件检测工序的温度相关的误差进行合适的误差校正。他们为一个两轴旋转中心用几何温度残余误差构造位置函数及机床的预处理特征参数,例如旋转精度、螺距、偏角、直线位移精度、平行度及正交误差等。Mou, Donmez, and Cetinkunt也对误差补偿应用了回归技术;然而,他们研究结果显示通过级和温度残余误差的理想补偿不能解释在零件加工与检测工序之间的偏差。从这项调查中,在准静态误差建模和试验误差控制中对机床相关温度控制已经有所改善是很明显的。用静态机床特征参数作为工序特征与控制是由合理是个很重要的问题。由于机床能够展现依靠负载循环的运行变化情况,所以独自运用准静态误差预测模型来达到补偿的目的的恰当性也是非常重要的。也就是说,因为设备参数很可能随着由热载荷变化引起的切削载荷而变化,从而产生估计工序误差和工序控制的准静态测量的实用性问题。检测在无载荷、循环载荷环境下测量结果和为精确补偿而作的模型预测误差之间的众多不同之处是不要的。正如前面所讲,这项研究检测的是在切削载荷循环下预测误差的建模和加工循环机床精度之间的变化。接下来将介绍决定该误差的理论模型。理论公式 在这部分,将该准静态误差模型作为实验机床。下面这些等式与总的准静态误差所提供的21项测量误差参数有关。图片一所展示的机床是XYFZ Ref. 4型号机床,其中F代表机床、Z代表刀具相对F在Z方向上的移动、X和Y代表工件相对F的运动方向。对于这种型号的机床,在X和Y方向上运动的工作台带动工件引起工件上一点P的平移和旋转误差。对于Z方向上的运动(刀具的运动),相对于机架的Z轴的平移误差和刀轴的旋转误差必须考虑。Enlarge 200%Enlarge 400%图片一 简图和传感元件的排列Enlarge 200%Enlarge 400%Enlarge 200%Enlarge 400%在图片二中,P表示随着工作台在XY方向上运动的工件上的一点。O点表示机床原点并且为机床参考点。P点由刀具Z方向上的运动来定位。用O“、Oz、O3和WO分别表示X、Y、Z和工件原点。工作台在XYZ方向上运动时,原点1、O2和O3平移和旋转(在图片2中展示了发生平移和旋转的O1和Oz点)。对于工作台在XY方向上运动,P点位置可以用该旋转矩阵表示。下面给出了XYZ矩阵及刀具偏置量。其中,su (V)是关于U轴在V轴运动下的旋转并切是逆时针正量。U(V)是表示由V方向运动引起U方向的平移误差。U和V可以由X、Y、Z代替。YX、ZY、ZX的输出方阵分别由as ay, azy和azx表示。T矩阵分别表示在X, Y和 Z方向上刀具偏置。因此该点的位置和总误差可以由下面给出的Eq. (1)中的替换矩阵确定。为达到这一点,与平移、旋转、直线误差及刀具偏置量相关的所有21个几何精度误差参数必须测定。然后这些值可以插入到下面出现的X, Y,和 Z位置的等式中去并且在X, Y, Z方向上的定位误差各等式右边项来计算。Enlarge 200%Enlarge 400%P点位置可以由替换程序坐标系(XY,Z)确定并且由等式中测定的几何精度参数来测定。然后系统误差就可以由各的右项的计算差来决定。上面的等式组成包括(X、Z)坐标点和位置、旋转、机床方阵误差等。为确定准静态影响的误差,试验确定21项误差参数并在等式中运用是必须的。一旦这些误差被认识,他们就可以与加工工件的最后检测工序相比较。接下来将介绍用于几何精度测定、加工测试和最后检测工序的实验设备。实验设备 这里讨论的实验细节对温度传感设备、静态机床特征、工件设计与循环参数和检测程序的进行描述。Enlarge 200%Enlarge 400%图片二 工作台行程的原位移和旋转在该项调查中,一台三轴数控铣床作为温度测量和切削力吉切削转距测量的设备。总计19个热点偶被用来随时测量机床结构温度。图片1是机床和传感元件位置的简图。图表一列出了在图片一种用于显示数字定位的热点偶。这些热电偶首先对实验进行标定,他们的定位是基于试验判定基础上的。对于静态特性,21项误差参数被确定(每轴6个误差项:沿运动轴的定位误差、沿相对该运动的其他两轴的直线度误差、倾斜误差、滚动误差、偏角误差及三轴之间的直线度误差)。一台激光干涉仪、一台电子水平仪及一台自动准直仪被用于分别测定各轴定位误差、滚动误差和偏角误差。另外的静态特性测定包括一个重复性测定、小负载影响下的设备滞后测定、在无负载情况下的心轴滑移测定,524 rpm, 和4000 rpm。所有特性测试都是以ANSI B5.54机床工作性能计算标准为基准的。切削测定是以一个加工过的光滑铝件、一个设置在符合ANSI B5.54标准的运输平板上底部重叠的工件进行的。加工方式包括铣削上表面、在工件周边铣削台阶、在测试工件中心铣削两个圆形槽以及用快铣、镗及逆镗方式加工36个孔。所有刀具都是HSS的。刀具路径图在图片3中展示、切削刀具和加工参数在表格2中列出。通过数据校准软件将测力计和温度传感器连接到一台用于再现校准和存储数据的PC机上。用一台并列的检测设备对成型零件进行规格测定。沿X和Y轴的重复性和直线度被计算出来。在检测之前零件的温度必须加以稳定。2号刀具在对36个镗孔和逆镗孔的最初加工过程的进给量4 ipm 和 5 ipm。对于3号刀具,8 ipm进给用于3.74, 2.52, 和 2.007中心槽的循环插值法。3、4、5号刀具另外4 ipm 和 5 ipm进给值用于中心槽的快速切削(3号)和成型镗及逆镗这些孔达到具体的深度。监控室温并使其变化维持在1 oC.内。结果与讨论在这部分中,测定结果与实际误差相比较、动态和准静态的重复性变化得以说明以及机床结构温度变化得以展示。预测误差与实际误差图4和图5对36个镗孔和逆镗孔中心在X和Y方向上的实际误差与模型误差进行了比较。镗孔和逆镗孔的理想中心位置和静态特性参数在Eq. (3)中被应用以计算在工件坐标系下中心位置误差。Enlarge 200%Enlarge 400%表一 热电偶的位置Enlarge 200%Enlarge 400%图片3 成型工件说明和刀具路径Enlarge 200%Enlarge 400%表二 刀具标准和加工参数Enlarge 200%Enlarge 400%图片4 X方向上的预测误差与实际误差Enlarge 200%Enlarge 400%图片5 Y方向上的预测误差与实际误差模型误差显示所有静态误差的综合影响是使1点在加工操作中相对他原始位置发生越位。图片6和图片7 可以解释这一点,图片中显示出X和Y方向运动的直线位移精度。工作台在整个行程中达不到程序设定点是很明显的。因此,当工作台沿X、Y轴移动并且刀具加工同时降低,该点将相对工件原点发生越位。实际镗孔和逆镗孔偏差也被看出是随孔位置变化的并且与模型误差没有关联。这些偏差暗示着从设备静态特性到动态特性的变化并且似乎也说明对具体程序的依赖性,也就是操作顺序和参数。在热负载环境下也存在着变化。下面介绍机场受热外形的测定和讨论。重复性分析图片8 显示出沿XY轴的重复性。沿一根轴的重复性可以作为对该轴在镗孔和逆镗孔坐标之间的不同之处被测定。例如,对1孔,沿X轴的重复性就是被测定的X轴镗孔尺寸减去逆镗孔尺寸。对于其他孔中心的重复性已经由XY轴确定。沿这两轴的重复性被发现是随孔位置变化的,该最大重复性误差是沿X轴 0.0011 和沿Y轴0.0008 。这些值是超出沿X方向11.5和Y方向5.2的长度的。这些值可以分别与准静态重复性0.000091 和沿X (20) 及Y (10)轴0.00004相比较。在图9中,量值与位置发生值是两种不同的情况。很明显无载荷重复性与切削载荷重复性也是非常不同的。在 Mou, Donmez, 和 Cetinkunt的工作中几何温度相关误差的建模与补偿不能解释工序相关误差是很明显的。工序相关误差取决于刀具偏差、机床变形、由热载荷引起的零件温度变化、材料属性、刀具耐磨性、冷却剂的影响以及环境的影响。机床结构部件和冷却剂输入输出的温度变化已经被指出对引起全面位置变化是很重要的。Enlarge 200%Enlarge 400%图6 X轴直线位移精度Enlarge 200%Enlarge 400%图7 Y轴直线位移精度Enlarge 200%Enlarge 400%图8 动力重复性测试结果Enlarge 200%Enlarge 400%图9 准静态重复性测试结果Enlarge 200%Enlarge 400%图10 单轴承温度变化Enlarge 200%Enlarge 400%图11 沿机架的温度变化Enlarge 200%Enlarge 400%图12 冷却剂的温度变化从结果可以看出在静态和动态机床特性参数及基于模型误差预测存在很重要的变化是很明显的。这些参数很可能依赖于切削环境。像这样的依赖环境,虽然以前提起过,但是还没有进行研究。从机床的设计、购置和用途观点看,对处在操作环境中的机床特性来说它们是非常重要的。这暗示着用准静态测量和建模而得到的机床的合格性和补偿性颗鹅能不适于工序误差的减小。例如,对于这台机床,准静态和载荷环境下对X轴的重复性分别是0.000091 和0.0011。这有很大的不同之处并且证实预处理机床特性可能不足以达到误差校准和控制的目的即使是在温度变化的环境中工作,由于实际切削环境引起热载荷缺乏。从运用负载循环的观点来观察机床特性是非常重要的,这又取决于不同的工作环境、刀具材料、进给量、进给速度、切削深度及外形特征。所有这些都可能产生不同的热负荷,从而导致参数变化。实际上静态特性是在最理性的环境下测定的;对又负有实际意义的机床特性来说,切削环境特性是非常重要的。这很明显可以从展示的数据看出。然而,在现实中,由于刀具材料、进给量、进给速度、切削深度及工件外形等众多不同加工因素的影响,一个符合特性的负载循环是相当困难的和耗时的。在道具和工件之间相对位移的可靠的实时测定也是相当困难的,即使可能,也取决于加工环境。一个合理的负载循环预测是来自在线程序输出,例如,动力、转距和温度等。因此, 一种可选择的途径是可以用分离工序误差来构造用于估计误差的模型,工序误差取决于工作中动力、转距传感器和刀具耐磨性测定而得到的偏差和变化。作者正验证这种方法。下面列出了一些相关的研究问题:分配与温度相关的误差量应考虑切削刀具的偏差和耐磨性,用于稳定环境的结构的与温度相关的偏差。在加工过程中,设备运转测试在不同的切削环境和对于不同的材料有着广泛的特征。构造机床精度参数模型作为一个负载环境函数。从以前的知识理论中发展一种基本的理论控制系统来预测和控制与温度相关的误差。结 论这项研究调查了在预测误差建模和加工循环机床精度间的变化。一台试验机床被予与准静态特点并且用它来加工一个铝制工件的外形。最后检验工序和数据分析说明了基于静态测量结果的误差不畅可能是不充分的。基于以上发现,一些重要的研究问题已经提出来了
- 温馨提示:
1: 本站所有资源如无特殊说明,都需要本地电脑安装OFFICE2007和PDF阅读器。图纸软件为CAD,CAXA,PROE,UG,SolidWorks等.压缩文件请下载最新的WinRAR软件解压。
2: 本站的文档不包含任何第三方提供的附件图纸等,如果需要附件,请联系上传者。文件的所有权益归上传用户所有。
3.本站RAR压缩包中若带图纸,网页内容里面会有图纸预览,若没有图纸预览就没有图纸。
4. 未经权益所有人同意不得将文件中的内容挪作商业或盈利用途。
5. 人人文库网仅提供信息存储空间,仅对用户上传内容的表现方式做保护处理,对用户上传分享的文档内容本身不做任何修改或编辑,并不能对任何下载内容负责。
6. 下载文件中如有侵权或不适当内容,请与我们联系,我们立即纠正。
7. 本站不保证下载资源的准确性、安全性和完整性, 同时也不承担用户因使用这些下载资源对自己和他人造成任何形式的伤害或损失。

人人文库网所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
|
2:不支持迅雷下载,请使用浏览器下载
3:不支持QQ浏览器下载,请用其他浏览器
4:下载后的文档和图纸-无水印
5:文档经过压缩,下载后原文更清晰
|
 川公网安备: 51019002004831号
川公网安备: 51019002004831号