人人文库网 > 图纸下载 > 毕业设计 > QD10t-31.5m箱形双梁桥式起重机起重小车的设计【word+7张CAD图纸全套】【优秀机械毕业设计】

车轮轴A3.dwg

QD10t-31.5m箱形双梁桥式起重机起重小车的设计【word+7张CAD图纸全套】【优秀机械毕业设计】

资源目录

QD10t-31.5m箱形双梁桥式起重机起重小车的设计【word+7张CAD图纸全套】【优秀机械毕业设计】.rar

侯跃龙目录及摘要封面.doc---(点击预览)

外文翻译

译文.doc---(点击预览)

机101侯跃龙.doc---(点击预览)

外文资料翻译封面及格式要求.doc---(点击预览)

~$101侯跃龙.doc---(点击预览)

cvt(无级变速器)英文文献.pdf---(点击预览)

压缩包内文档预览：

编号：294791 类型：共享资源大小：3.13MB 格式：RAR 上传时间：2014-07-03 上传人：QQ14****9609 IP属地：陕西

45
积分

版权申诉 word格式文档无特别注明外均可编辑修改；预览文档经过压缩，下载后原文更清晰！ 立即下载

关键词：: qd10t 箱形双梁桥式起重机起重小车设计 word cad 图纸全套优秀优良机械毕业设计

资源描述：

QD10t-31.5m箱形双梁桥式起重机起重小车的设计【word+7张CAD图纸全套】【优秀机械毕业设计】

【带外文翻译】【57页@正文17970字】【详情如下】.bat

侯跃龙目录及摘要封面.doc

卷筒图A2.dwg

吊钩图A3.dwg

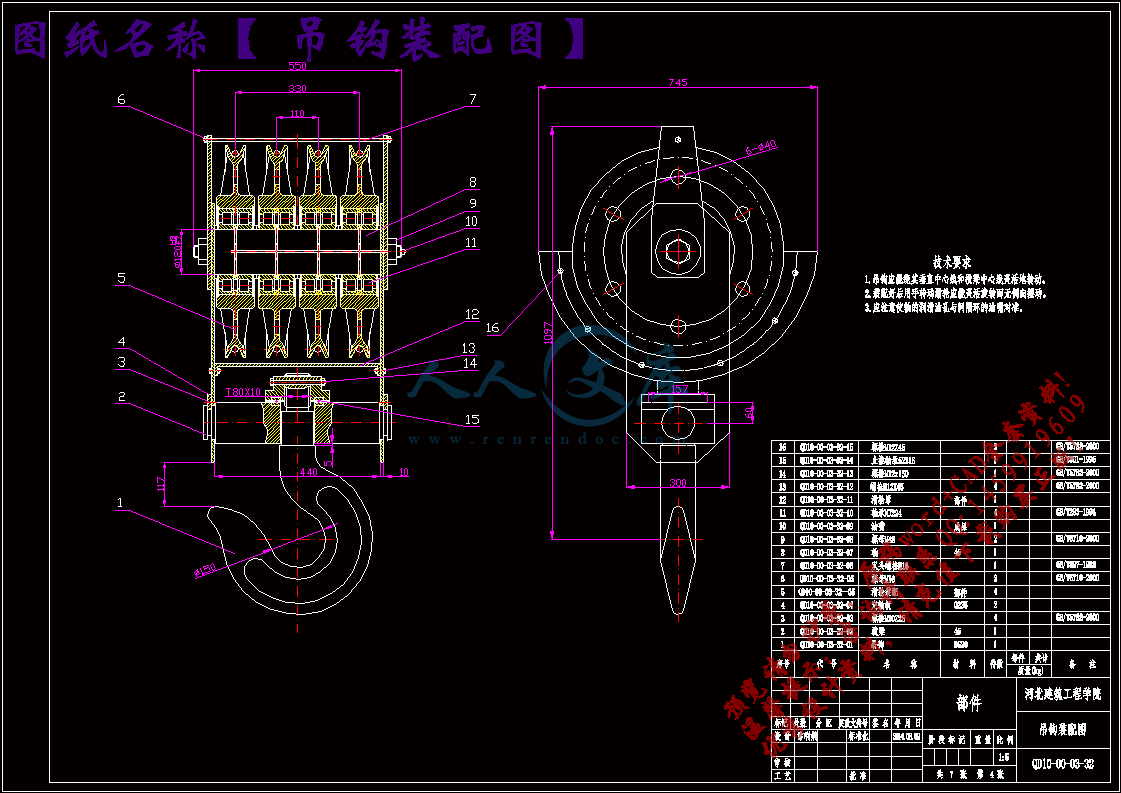
吊钩装配图.dwg

外文翻译

封面.doc

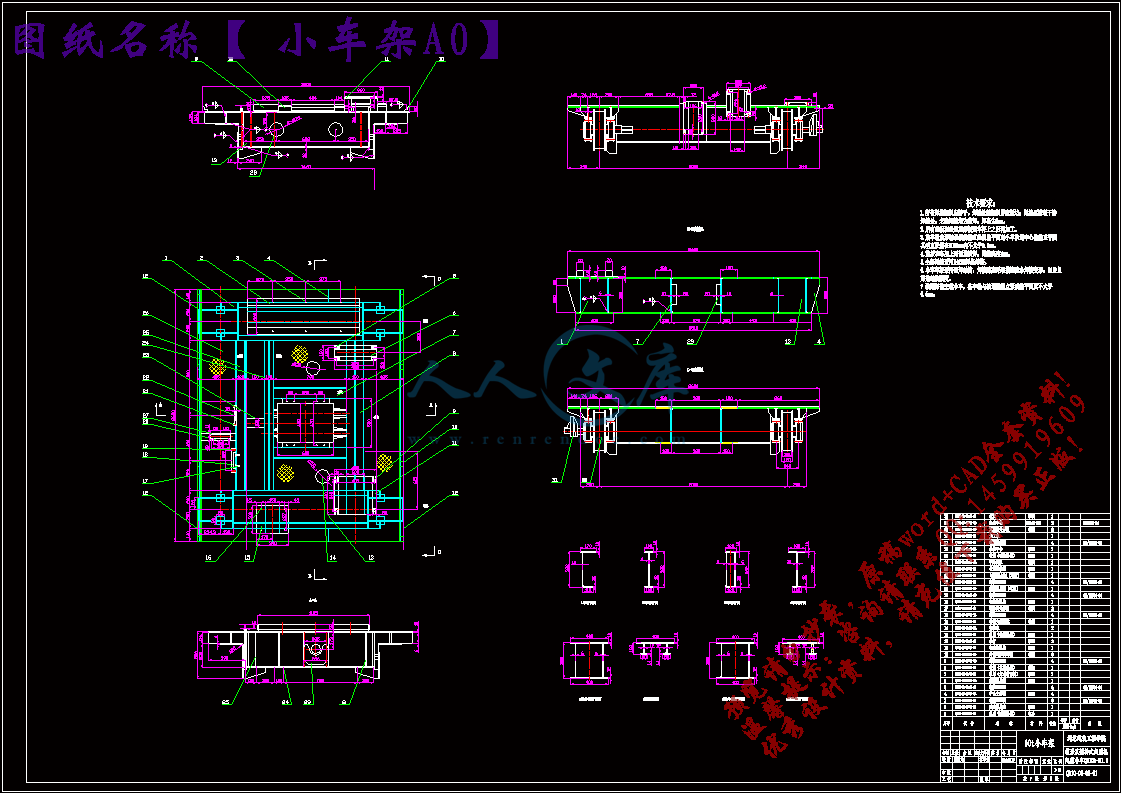
小车架A0.dwg

小车装配图A0.dwg

正文.doc

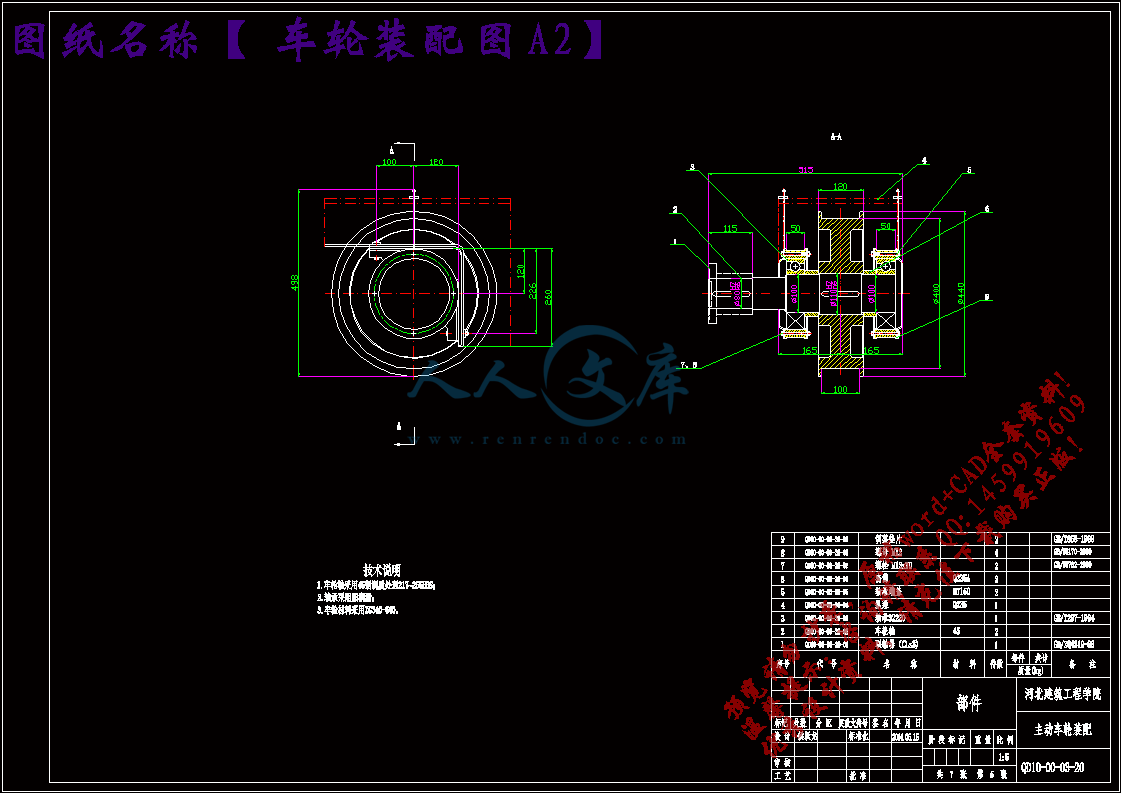
车轮装配图A2.dwg

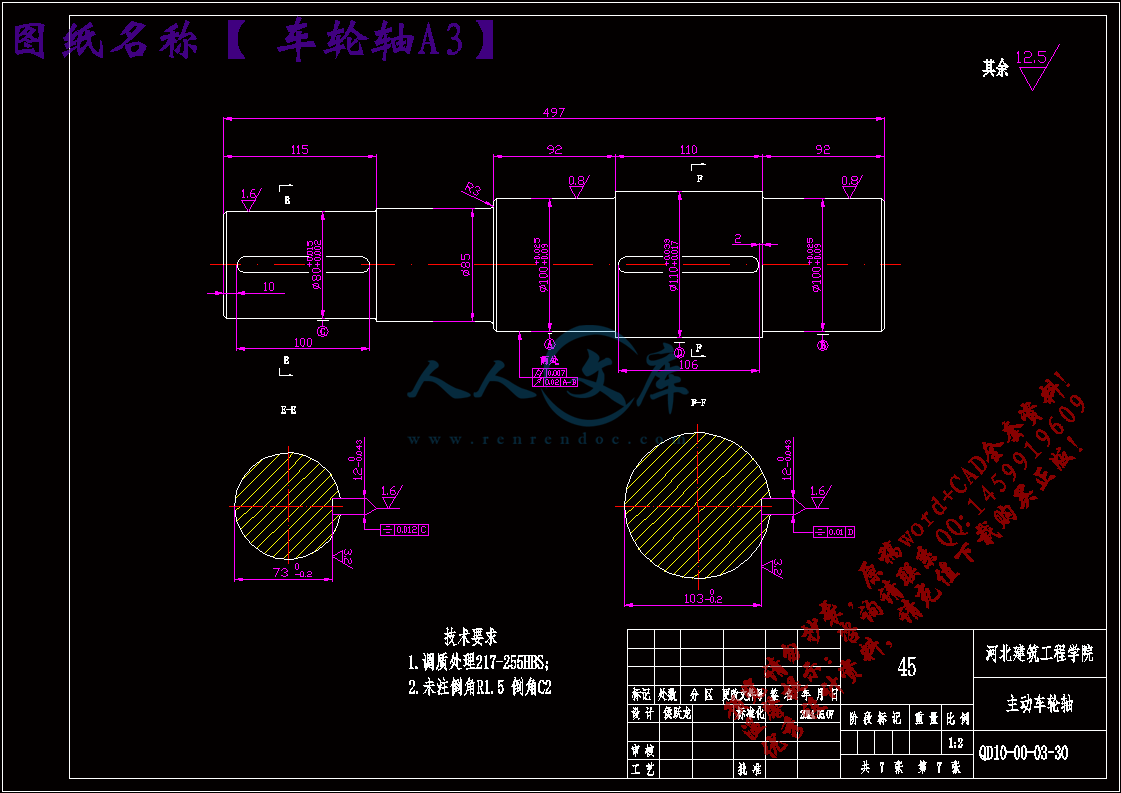
车轮轴A3.dwg

第1章前言1

1.1 国内外起重机发展情况1

1.2 桥式起重机定义及特点4

1.3 实习地点及实习内容4

第2章总体设计4

2.1 概述5

2.2 传动方案的确定6

2.3 基本参数10

第3章起升机构的设计计算12

3.1 选择钢丝绳12

3.2 滑轮和卷筒的计算13

3.3 计算静功率15

3.4 选择电动机15

3.5 验算电动机的发热条件15

3.6 减速机的初选16

3.7 校核减速机16

3.8 制动器的选择17

3.9 联动器的选择17

3.10 验算起动时间18

3.11 浮动轴强度验算19

第4章运行机构的设计计算21

4.1 确定机构传动方案21

4.2 选择车轮与轨道并验算其强度21

4.3 运行阻力计算23

4.4 选择电动机24

4.5 验算电动机发热条件25

4.6 选择减速器25

4.7 验算运行机构和实际所需功率25

4.8 验算起动时间26

4.9 验算起动不打滑条件27

4.10 制动器的选择27

4.11 选择联轴器28

4.12 验算低速浮动轴强度29

第5章零部件的设计计算31

5.1 滑轮的尺寸计算与选择31

5.2吊钩组的选择32

5.3 车轮轴的设计计算35第6章零部件的设计计算38

6.1 梁Ⅰ38

6.2 梁Ⅱ40

6.3 梁Ⅲ42

6.4 梁Ⅵ44

6.5 梁Ⅴ48

第7章毕业设计小节53

参考文献54

附：英文原文

英文译文

毕业实习报告

第1章前言

1.1国内外起重机发展概况

起重运输机械行业在我国从上世纪五六十年代开始建立并逐步发展壮大，该行业已形成了各种门类的产品范围和庞大的企业群体，服务于国民经济各行业。随着我国经济的快速发展，起重运输机械制造业也取得了长足进步。2005年起重运输机械行业销售额达到1272亿元，“十五”期间平均每年增长超过30％，2006年依然保持着持续增长的态势，目前市场前景非常好。近年来，国家重点发展能源（其中煤炭工业迅猛发展，起重运输机械制造业将提供所需的竖井提升设备、斜井防爆下运带式输送机、防爆移置式带式输送机、装车机、露天矿连续开采输送设备、用于洗选设备的各种输送设备等）、电力（各种电站专用桥式/门式起重机、料场用物料搬运装卸设备、输煤给煤栈桥内物料输送设备、环保排灰输送设备、水电站用闸门启闭机械、升船机、核电站废料处理专用起重机等将有较大需求）、石化（起重运输机械制造业将提供所需的自动灌装和包装码垛设备、仓储专用设备、厂内和车间内物料搬运装卸设备等）、冶金（对各种冶金起重机、厂内和车间内物料搬运装卸设备、料场堆取料与混匀料设备等将有较大需求）、造船、交通等工业领域（需要大量的高效、节能、低污染、智能化、柔性化、成套化的物料搬运装卸设备）。

十一五”期间，我国起重运输机械产品的工业总产值、销售收入和利润总额的年平均增长率将超过15％。到2010年，该行业的工业总产值将达到2670亿元，销售收入将达到2560亿元，利润总额将达到148亿元；出口额约达65亿元，平均年增长11％；而国内市场增长的速度会呈逐年小幅递减趋势，其主要原因是国内市场开放程度大幅度提高、而行业又均

受到发达国家技术壁垒等限制；另一方面我国市场对高质量高水平的起重运输机械需求旺盛，而我国行业的技术竞争能力有待提高。政府主管部门应加强对起重运输机械行业的政策引导和管理，树立规模生产方式。国家应重点培育3～4个起重运输机械集团和重点配套件的生产体系，加大技术改造的力度，提升装备水平，保证产品质量，提高生产效率，降低制造成本，提高市场竞争力。培育自主创新能力，走引进国外先进技术、消化吸收再创新、集成创新的道路。发展自主品牌的新产品，替代进口产品，并出口国际市场，参与国际竞争。2010年力争有25％～30％的产品接近或达到国际先进水平。树立品牌意识，推进名牌战略，努力创建中国名牌产品、行业名牌产品。充分认识“科技是第一生产力”的观点。建立各类行业培训中心，加强对重点骨干企业、起重机械制造基地的管理干部、科技人才和高级技工的培训。树立知识产权意识，加大保护知识产权的力度，严厉打击各种违法行为，有利于调动广大科技人员和企业创新的积极性。加强调整各级行业协会，选拔一批有科技、生产、企业管理经验的专职人员充实到各级行业协会。行业协会要积极推行职业化、专业化、年轻化，配合国务院有关部门加强对行业的管理。

在国外，尤其是美国、日本和西欧的一些发达国家，机械产品的结构优化已有几十年的历史，门桥式起重机已完全采用了模块化设计，它可以根据用户对设备起重量、起升高度和轨道跨距等主参数的要求，并结合用户现场的实际空间和工作环境特点，直接调用参数化3D模型进行现场组装，然后对起重机结构进行有限元分析和优化，直到满足用户的要求。而在国内，由于主梁结构比较复杂，传统的设计方法很难分析主梁局部应力和变形，使一些真正危险点被忽略，或对一些本已比较安全的部位无畏地加大或加厚，造成材料的浪费和生产成本的增加，不利于产品的市场竞争。因此，对门桥式起重机主梁结构的有限元分析和优化具有很重要的现实意义。另外，随着社会的进步，环保意识和劳动保护意识的提高，冶金起重机设计过程中把人机工程及操作环境舒适要求提到了较高的要求，如：司机室加装冷、暖空调、隔热保护、地面无线遥控、车上有线和无线通讯、航空座椅、司机休息室，上、下吊车全部采用斜梯、电气室加装隔热防护和冷风机，较窄的人行通道采取防滑措施，经常检修部分加装吊笼等都为操作维护人员提供了较好的工作环境和条件。特别是双层壁、双层玻璃的司机室与可躺式航空座椅、冷暖空调、有线、无线通讯配合使用。为改善司机的工作条件、提高工作效率、减少工作失误起到了很好的作用。人机工程合理化正逐步成为现代冶金起重机发展的主要趋势之一，越来越引起人们的重视。

桥架、小车架整体加工的应用。桥架、小车架包括一些大型结构件整体加工是保证冶金起重机产品质量的一项重要措施和有效途径。由于冶金起重机工作的特殊性，对质量提出了较高的要求，小车架整体加工指焊在小车架上的电动机底座，制动器底座，减速器支承座，卷筒支承座，和小车车轮支承座等机座一次性地划线加工而成，相互间的形位、尺寸公差由机床保证，因此装配工作变得特别简单。只要把电动机、制动器、减速器、卷筒、车轮就位即可，不像旧的办法，它们间的形位、尺寸误差靠塞垫片来调节。简而言之，这些部件间的形位公差由机床精度保证与装配工人的技术等级无关，排除了人为因素，因而大大提高了装配精度和使用性能，同时也大大缩短了用户的维修时间。

我们认为未来中国起重机的几个发展趋势如下：

1、重点产品大型化、高速化、耐久化和专用化

2、系列产品模块化、组合化、标准化和实用化

3、通用产品小型化、轻型化、简易化和多样化

4、产品性能自动化、智能化、集成化和高效化

5、产品组合成套化、系统化、复合化和信息化

6、产品设计微机化、精确化、快速化和全面化

7、产品构造新型化、美观化、宜人化和综合化

8、产品制造柔性化、灵捷化、精益化和规模化

1.2桥式起重机定义及特点

取物装置悬挂在可沿桥架运行的起重小车或运行式葫芦上的起重机，称为“桥架型起重机”；桥架两端通过运行装置直接支撑在高架轨道上的桥架型起重机，称为“桥式起重机”。

桥式起重机一般由装有大车运行机构的桥架、装有起升机构和小车运行机构的起重小车、电气设备、司机室等几个大部分组成。外形像一个两端支撑在平行的两条架空轨道上平移运行的单跨平板桥。起升机构用来垂直升降物品，起重小车用来带着载荷作横向运动；桥架和大车运行机构用来将起重小车和物品作纵向移动，以达到在跨度内和规定高度内组成三维空间里作搬运和装卸货物用[3]。

桥式起重机是使用最广泛、拥有量最大的一种轨道运行式起重机，其额定起重量从几吨到几百吨。最基本形式是通用吊钩桥式起重机，其他形式的桥式起重机基本上都是在通用吊钩桥式的基础上派生发展出来的。

1.3实习地点及实习内容

毕业实习是在张家口市神力起重设备有限公司对QD16t/20t双梁桥式起重机小车进行了参观实习。

第2章总体设计

2.1 概述

总体设计是机械设计中极为关键的环节，它是对机器本身总的设想。总体设计的成败关系到整部机器的经济技术指标，直接决定了机械设计的成败。

总体设计指导机构设计和零件设计的进行至关重要。在接受设计任务后进行细致的调查研究，收集国内外同类机械的有关资料了解国内外的使用、生产、设计和科研情况，并进行分析比较，制定总体设计原则。设计原则应当保证所设计的机型符合有关的方针、政策。在满足使用要求的前提下，力求结构合理，经济性好，寿命长，同时还应考虑到绿色环保和操作的舒适安全。

总体设计应遵循以下原则：

1.遵循“三化”原则：零件标准化，产品系列化，部件通用化。

2.采用“四新”原则：新技术，新工艺，新结构，新材料。

3.满足“三好”原则：好造，好用，好修。

好造,即具有良好的工艺性，制造简单；好用，即具有良好的使用性能，表现为生产率高,操作轻便，机动灵活，安全而且耐用可靠；好修，即一旦发生故障，易于拆卸，维修护理方便。

4.对部件设计和零件设计负责的原则。把各部件的设计制造特点作为部件和零件指导性文件，必须为零部件的设计人员创造方便条件，而零部件设计必须满足总体设计提出的工作条件、尺寸、性能参数等方面的要求。

制定设计总则以后，便可以编写设计任务书。在调研的基础上，运用所学的知识，从优选择，确定总体参数，保证设计的成功。

2.2 传动方案的确定

箱式双梁桥式起重机主要组成部分有小车（起升机构，小车运行机构和小车架），桥架（主梁，端梁，走台和护栏等），大车运行机构和司机室（操纵机构和电器设备等）等部分组成。

桥式起重机的运动，是由大车的纵向，小车的横向及吊钩的上下三种运动组成的。有时是单一的运动，有时是合成的动作。他们都有各自的传动机构来保证其运动形式的实现。

2.2.1起升机构的传动原理

起升机构的传动原理:起升机构的动力来源是由电动机产生，经齿轮联轴器，浮动轴，制动轮联轴器，将动力传递给减速器的高速轴端，经减速器把电动机的高转数降低到所需的转数之后，由减速器低速轴输出经卷筒上的齿轮联轴器把动力传递给卷筒组，再经过钢丝绳和滑轮组使吊钩进行升降，从而完成升降重物的目的。

2.2.2起重小车运行系统的传动原理

起重小车运行系统的传动原理动力由电动机产生，经制动轮联轴器，立式二级减速器的高速轴，并经立式二级减速器把电动机的高转数降低到所需要的转数之后，再由低速轴端输出，经半齿联轴器传到驱动轮，再有驱动轮的另一端经半齿联轴器通过浮动轴，半齿联轴器传到另一驱动轮。从而带动了小车驱动轮的旋转，完成小车的横向运送重物的目的。

2.2.3大车运行系统的传动原理

动力由电动机发出，经制动轮联轴器，补偿轴和半齿联轴器将动力传递给减速器的高速轴端，并经减速器把电动机的高转数降低到所需要的转数之后，由低速轴传出，又经全齿联轴器把动力传递给大车的主动车轮组，从而带动了大车主动车轮的旋转，完成桥架纵行吊运重物的目的。大车两端的驱动机构是一样的。

原有双梁桥式专用起重机的大车运行机构机构是由四个电机驱动的，电机较多，机构比较繁杂，这给安装和维修带来了许多不便，同时也提高了生产成本，改进后只在两梁的两侧分别安装一个电机，适当提高电机功率，由两对主、被动车轮组成。在不影响行走性能的前提下，精简了机构，减少了故障率，易于安装维修，电机的减少有效地降低了成本。

2.2.4设计小车的基本原则和要求

箱形双梁桥式起重机由两根箱形主梁和两根横向端梁构成的双梁桥架，在桥架上运行起重小车，可起吊和水平搬运各类物件，其中主梁做横向移动，小车做纵向移动从而使起重机的工作范围扩展到一个立方形空间。

箱形双梁桥式起重机一般由起重小车、桥架运行机构、桥架金属结构组成。而起重小车主要由起升机构、小车运行机构和小车架以及限位安全装置等组成。

在设计桥式起重机小车时，必须力求满足以下几方面的要求:

1、整台起重机与厂房建筑物的配合以及小车与桥架的配合要适当。小车与桥架的互相配合，主要在于小车轨距和桥架上的小车轨距应相同；其次，小车上的缓冲器与桥架上的挡铁位置要配合好，小车上的撞尺和桥架上的行程限位开关要配合恰当。小车的平面布置愈紧凑，小车到桥架的两端愈远，起重机工作范围也就愈大。小车的高度小，相应地可使起重机的高度减小，从而可降低厂房建筑物的高度。

2、小车上机构的布置及同一机构中各零部件间的配合要求适当。起升机构和小车运行机构在小车架平面上的布置要合理紧凑，但二者之间的距离不应太小，否则维修不便，或造成小车架难以设计。

3、小车车轮的轮压分布要求均匀。如能满足这个要求，则可以获得最小的车轮、轴承及轴承箱尺寸，并且使起重机桥架主梁受到均匀的轮压载荷。一般最大轮压不应超过平均轮压的20%。

4、小车架上的机构与小车架结构的配合要适当。为使小车上的起升、运行机构与小车架配合的好，要求二者之间的配合尺寸相符；联接零件要选择适当和安装方便。在设计原则上，要以机构为主，应尽量用小车架去配合机构；同时机构的布置也要尽量使钢结构的设计制造方便。因为小车架是用来安置与支撑起升机构和小车运行机构的，所以小车架要按照起升和运行机构的要求设计，但在不影响机构工作的条件下，机构的布置也应配合小车架的设计，使其构造简单、合理和便于制造。

5、尽量选用标准零部件，以提高设计与制造的工作效率，降低生产成本。

6、小车各部分的设计应考虑制造、安装和维护检修方便，要尽量在不需移动邻近部件的条件下，能将各部件拆下修理。

桥式起重机小车主要由起升机构、小车运行机构和小车架三部分组成。另外，还有一些安全防护装置。

我国制造的桥式起重机的小车具有下列特征；

1、起升和运行机构由独立的部件构成。这些部件之间用补偿联轴器联系起来。齿轮联轴器补偿了转轴中心线的偏移和歪斜，这些偏差和歪斜系因制造与安装不精确，以及小车架变形而产生部件间彼此位移所引起的。由于采用了分组的独立部件，因此，使小车上各机构的装拆方便。

2、在设计机构和小车时，遵循“三化”（标准化、通用化和系列化）的原则。这可使零部件的互换性得到保证，降低制造和使用维护起重机的费用，并使所需零部件的备品量减到最少。

3、小车架用钢板焊接而成。在车架上焊有底板。电动机、减速器、制动器和和可拆卸的轴承座等均安装在这种底板上。为了简化车架的加工，底座的加工面应尽量布置在同一水平面或垂直面上。

4、起升机构和运行机构采用减速器式传动装置。

起重机小车除有起升、运行机构和小车架外，还必须有必要的安全保护装置:如栏杆、排障板、撞尺、缓冲器、和限位开关等。其具体要求分述如下:

1、栏杆栏杆设置在与小车轨道相垂直的小车台面边缘上。为了便于维修上下，在小车的另外两侧不设栏杆。栏杆可用角钢或钢管制作，高度不低于1米，并应设有间距为350㎜的水平横杆，底部应设有不小于70㎜高的围护板。

2、排障板排障板装在小车架端梁两端的车轮外边，用于推开小车轨道上可能有的障碍物，以利于小车运行。

2、限位开关用于限制吊钩和小车架的极限位置。在起升机构中，限位开关用于限制吊钩向上运行位置，使其不能碰到小车架。小车运行机构的行程限位开关，安装在起重机桥架主梁的两端，位于小车轨道外侧的主梁盖板上。在小车架相应的端梁外侧

固定着一根用角钢弯折的撞尺。当小车运行至极限位置时，撞尺压迫限位开关的摇柄转动30°，使开关盒内的触点断开，于是运行机构的电动机断电。由于接线关系，此时电动机只能作反向运行。

3、超载限制器起升机构超载限制器应保证载荷不超过其额定值的10%，工作精度为2~3%。

起重机小车的设计主要是对起升机构、小车运行机构、小车架的设计以及包括栏杆、高度限位器、负载限制器和行程开关等在内的安全装置分析与计算，并在原有设计的基础上做出改进，并解决原来起重机上存在的影响工作性能的结构，并尽可能降低成本。

最终设计出优化产品。

2.3 基本参数

1.额定起重量(Q)

起重机正常工作时允许一次起升的最大重量称为额定起重量，单位为吨（t）或千克，常用符号Q、P或CP等表示。桥式起重机的额定起重量是定值。当额定起重量不只一个时，通常称额定起重量为最大起重量，或简称起重量。

额定起重量:Q=10t

2.起升高度(H)

起升高度是指从地面至取物装置最高位置的铅垂距离（吊钩的钩环中心），单位为米。

起升高度:H=12m

3.跨度(L)与轨距(l)

桥式起重机大车运行轨道中心线之间的水平距离称为跨度（L），小车运行轨道中心线之间的水平距离称为轨距。

跨度为：L=31.5 m

轨距为：l=2 m

4.工作级别

确定起重机的工作级别是为了对起重机金属结构和结构设计提供合理的基础，为和客户进行协商时提供一个参考范围，它能使起重机胜任它需要完成的工作任务。由利用等级和载荷状态两个因素来确定起重机的工作级别。

工作级别为A5

5.起重机利用等级

起重机在有效寿命期间有一定的总工作循环数。起重机作业的工作循环是从准备起吊物品开始，到下一次起吊物品为止的整个作业过程。工作循环总数表征起重机的利用程度，它是起重机分级的基本参数之一。

起重机利用等级为U5

6.工作速度

起重机机构工作速度根据作业要求而定。

主起升速度：V1=13.3m/min

小车运行速度：V3=43.8m/min

大车运行速度：V2=112.5m/min

第3章起升机构的设计计算

由已知条件：工作级别A5，起重机利用等级U5，主钩额定起重量10t。

参考文献【1】P7表1-8得起重机为中级工作类型，JC%=25

参考文献【1】P50表4-3得安全系数K=5.5，=25（固定式）

参考文献【1】P65表4-14得选双联滑轮组X=2，倍率m=3

参考文献【3】表2-1得滑轮组的效率=0.985

参考文献【2】P230查附表8选图号为G15吊钩组，得其重量=219kg,两动滑轮间距A=185mm

参考文献【1】P50式4-4换算系数=0.85（6×19）=0.82（6×37）

1.选择钢丝绳

计算钢丝绳最的大静拉为

钢丝绳破断拉力为:

=5.5×17.29=95.1KN

查参考文献【2】P224附表1选用瓦林吞型纤维芯钢丝绳6×19W+FC，钢丝公称抗拉强度1670MPa，光面钢丝，左右互捻，直径d=14mm，钢丝绳最小破断拉力[]=108KN，标记如下：

钢丝绳14NAT6×19W+FC1770ZS108GB8918-88

滑轮的许用最小直径

图3-1起升钢丝绳缠绕简图

=14（25-1）=336mm

参考文献

【1】华玉洁主编. 起重机械与吊装. 北京. 北京工业出版社

【2】陈道南. 起重机课程设计. 北京科技大学：冶金工业出版社，1993.10

【3】陈道南等编. 起重运输机械. 冶金工业出版社，1988

【4】起重机设计手册编写组编. 起重机设计手册. 机械工业出版社：1979

【5】陈国璋编. 起重机计算实例. 北京. 中国铁道出版社

【6】起重机计算实例. 中国标准出版社，1984

【7】GB6067-85 起重机械安全规程.

【8】GB/T14405-93 通用桥式起重机. 北京：中国标准出版社，

【9】GB3811-83 起重机设计规范.

【10】JB/T6392.2-92 起重机车轮技术条件.

【11】董刚等主编．机械设计—3版．北京：机械工业出版社，1998

【12】机械设计手册编委会主编．机械设计手册（第二卷）．北京：机械工业出版社，2004

【13】成大先主编.机械设计手册.单行本.轴及其联接.北京：化学工业出版社，2004

【14】成大先主编．机械设计图册（第一卷上册）．北京：化学工业出版社，1997

【15】成大先主编．机械设计图册（第一卷下册）．北京：化学工业出版社，1997

【16】陆玉，何在洲，佟延伟编．机械设计课程设计.北京：机械工业出版社，2003

【17】（日）坂本种芳，长谷川政弘著，池成渊译，傅东明校，桥式起重机设计计算.北京：中国铁道出版社，1987

【18】余厚极编著.起重机吊装安全技术.北京：中国建材工业出版社，1998.11

【19】华玉溪主编.起重机械与吊装.北京：化学工业出版社，2005.8

360桌面截图20140703194010.gif

360桌面截图20140703201607.gif

车轮轴A3.gif

车轮装配图A2.gif

吊钩图A3.gif

吊钩装配图.gif

卷筒图A2.gif

小车架A0.gif

小车装配图A0.gif

内容简介：: Vehicle System DynamicsVol. 44, No. 5, May 2006, 387406Control of a hydraulically actuated continuouslyvariable transmissionMICHIEL PESGENS*, BAS VROEMEN, BART STOUTEN, FRANS VELDPAUSand MAARTEN STEINBUCHDrivetrain Innovations b.v., Horsten 1, 5612AX, The NetherlandsTechnische Universiteit Eindhoven, PO Box 513, 5600 MB Eindhoven, The NetherlandsVehicular drivelines with hierarchical powertrain control require good component controller tracking,enabling the main controller to reach the desired goals. This paper focuses on the development ofa transmission ratio controller for a hydraulically actuated metal push-belt continuously variabletransmission(CVT),usingmodelsforthemechanicalandthehydraulicpartoftheCVT.Thecontrollerconsists of an anti-windup PID feedback part with linearizing weighting and a setpoint feedforward.Physical constraints on the system, especially with respect to the hydraulic pressures, are accountedfor using a feedforward part to eliminate their undesired effects on the ratio. The total ratio controllerguarantees that one clamping pressure setpoint is minimal, avoiding belt slip, while the other israised above the minimum level to enable shifting. This approach has potential for improving theefficiency of the CVT, compared to non-model based ratio controllers.Vehicle experiments show thatadequate tracking is obtained together with good robustness against actuator saturation. The largestdeviations from the ratio setpoint are caused by actuator pressure saturation. It is further revealed thatall feedforward and compensator terms in the controller have a beneficial effect on minimizing thetracking error.Keywords: Continuously variable transmission; Feedforward compensation; Feedback linearization;Hydraulic actuators; Constraints1.IntroductionThe application of a continuously variable transmission (CVT) instead of a stepped transmis-sion is not new.Already in the 50sVan Doorne introduced a rubberV-belt CVT for vehiculardrivelines. Modern, electronically controlled CVTs make it possible for any vehicle speed tooperate the combustion engine in a wide range of operating points, for instance in the fueloptimal point. For this reason, CVTs get increasingly important in hybrid vehicles, see forexample 13. Accurate control of the CVT transmission ratio is essential to achieve theintended fuel economy and, moreover, ensure good driveability.The ratio setpoint is generated by the hierarchical (coordinated) controller of figure 1. Thiscontroller uses the accelerator pedal position as the input and generates setpoints for the localcontrollers of the throttle and of the CVT.*Corresponding author. Email: pesgensdtinnovations.nlMichiel Pesgens was previously affiliated with Technische Universiteit Eindhoven.Vehicle System DynamicsISSN 0042-3114 print/ISSN 1744-5159 online 2006 Taylor & Francishttp:/www.tandf.co.uk/journalsDOI: 10.1080/00423110500244088388M. Pesgens et al.Figure 1.Hierarchical powertrain control.The CVT and its hydraulic actuation system are depicted in figures 2, 3. The hydraulicsystem not only has to guarantee good tracking behavior of the CVT but also has to realizeclamping forces that, on the one hand, are high enough to prevent belt slip but, on the otherhand, are as low as possible to maximize the transmission efficiency and to reduce wear. Inpractice, the clamping forces levels are kept at levels that avoid belt slip at all times, whilestill maintaining an acceptable degree of transmission efficiency.ThemainfocusofthispaperisontheratiocontroloftheCVT,usingthehydraulicactuationsystem of figure 3. The presented control concept is based on the work of 3, 4. It enablestracking of the ratio setpoint, while guaranteeing at least one of the two pulley pressuresetpoints to be equal to its lower constraint. Even though the controller effectively changesfrom controlling one of the two pressures to the other, no actual switching between differentcontrollers takes place. Among the approaches seen in the literature, some incorporate aswitching algorithm 3, 5, whereas others control only one of the two (usually the primary)pressures 6, 7. Although the former approach cannot guarantee one of the two pressures tobe equal to its lower constraint, the latter cannot explicitly prevent the uncontrolled pressureto stay above its lower constraint.The rest of this paper is organized as follows. First, a mathematical model is derived forthe mechanical part of the CVT in section2. Next, in section3, the hydraulic part is modeled.The physical constraints, imposed by the hydraulic system, are discussed in section4. Theseconstraints are taken into account by the CVT ratio controller, that is developed in section5Figure 2.Variator.Hydraulically actuated CVT389Figure 3.Variator with hydraulic system.and is based on the earlier derived models for the mechanical and the hydraulic CVT parts.The tracking performance of this controller is experimentally evaluated in section6. Finally,section7 gives some concluding remarks.2.The pushbelt CVTThe CVT (figure2) considered here is equipped with a Van Doorne metal pushbelt. Thisbelt consists of a large number (around 350) of V-shaped steel block elements, held togetherby a number (between 9 and 12) of thin steel tension rings. The belt runs on two pulleys,namely the primary pulley at the engine side and the secondary pulley at the wheel side. Eachpulleyconsistsofoneaxiallyfixedandonemoveablesheave,operatedbymeansofahydrauliccylinder.Thecylinderscanbepressurized,generatingaxialforces(clampingforcesorthrusts)on the belt, necessary for transmission of torque (without macro-slip of the belt) and for ratiochange. Here the distinction is made between micro-slip, needed for torque transfer betweenbelt and pulleys, and macro-slip, which should be avoided at all times for its negative effecton efficiency and especially the risk of severe belt and pulley wear 8.The bounded transmission ratio rcvt rcvt,LOW,rcvt,OD is defined here as the ratio ofsecondary pulley speed sover primary pulley speed p, so:rcvt=sp(1)In deriving the variator model, it has been assumed that the pulleys are rigid and perfectlyaligned, and that the V-shaped blocks are rigid and the steel rings are inextensible. The beltis assumed to run in perfect circles on the pulleys. Further, it has been assumed that theclamping forces are large enough to prevent macro belt slip. The effects of micro-slip arerelatively small with respect to the ratio change behavior of the CVT, and are, therefore,neglected in the model. The power transmission between the belt and the pulleys is modeledas Coulomb friction (which is assumed in the majority of CVT variator research 3).390M. Pesgens et al.Using these assumptions, the running radii Rpand Rsof the belt on the primary andsecondary pulleys are functions of the ratio rcvtonly and are related by:Rp= rcvtRs(2)The axial position s( = p for the primary pulley, = s for the secondary one) of themoveable pulley sheave of pulley is also completely determined by the ratio rcvt. Denotingthe taper angle of the conical sheaves by (see figure 4), it is easily seen that sis given by:s= 2 tan() (R R,min)(3)Subscript max (or min) implies the maximum (or minimum) value possible, e.g. Xmax=max(X), unless stated otherwise. Differentiation with respect to time yields the axial velocity sof the moveable sheave of pulley s= (rcvt) rcvt(4)where the function follows from the geometry of the variator.Assuming that the radial friction force component between the pulley and the belt is zero,the critical pulley clamping force (equal for both pulleys, neglecting the variators efficiency)is given by references 3, 5 (for pulley ):Fcrit=cos() |T|2 R(5)where Tis the net transmitted torque between belt and pulley and is the coulomb frictioncoefficient between pulleys and belt. The factor 2 appears, as there are two friction surfacesbetween pulley and belt.Radial forces between belt and pulleys can be mainly contributed to centrifugal forces andCoriolis forces. In the detailed thrust force model of ref. 9, it is reported that even if thesliding angle (and hence the friction force angle) between the belt path and the friction forcevectorchangesalongthepulleycircumference,itsvalueconvergesrapidlytowardsvalueslessthan 10. As a result, the angle is assumed zero. The friction force angle would enter intoequation(5) as a multiplication factor cos(), which rapidly converges to 1 for small angles.For the choice of , a worst-case approach is applied. It is chosen as the maximum of thetractioncurve(ofwhichseveralhavebeenpresentedinref.10),whichisthepointoftransitionfrom micro-slip to macro-slip. The lowest value of all the maxima found in ref. 10, as wellas in ref. 8 (for both very similar variators) is 0.09, the value of that has been used here.Figure 4.Pulley sheave definitions.Hydraulically actuated CVT391The torque ratio is the ratio of transmitted torque and maximally transmittable torquewithout belt slip for pulley :=TT,max=cos() T2 RF(6)As in a practical vehicle application a good estimate of the torques acting on the secondarypulley is not available, the following modified torque ratio is introduced:?s=cos() Tp2 RpFs(7)The estimated primary transmitted torqueTpcan be obtained from the dynamic drivelineequations together with engine and torque converter characteristics (also see section 4). Incase of a perfect torque estimation, i.e.Tp= Tp, it is easily seen that (using equation(6):?s=PpPss(8)with transmitted power P= T. As it has been assumed that Pp= Ps, the modifiedtorque ratio becomes equal to the torque ratio for the secondary pulley.An important part of the model for the mechanical part of the CVT is the sub-model for therateofratiochangeasafunctionof,forinstance,theclampingforces.Sub-modelsofthistypeare proposed, among others, by Guebeli et al. 11, Ide et al.12, 13 and Shafai et al. 14.The blackbox model of Ide is preferred here, as it reasonably describes the results of a seriesof experiments with metal V-belt CVTs 3, 4.The steady state version of Ides model yields a relation for the primary clamping force Fpthat is required to maintain a given ratio rcvtwith a given secondary clamping force Fsand agiven primary torque Tp(through the modified torque ratio ?s):Fp= (rcvt,?s) Fs(9)For obvious reasons, the quantity in equation(9) is called the thrust ratio. Some experimen-tally obtained results for this highly non-linear function of the CVT ratio rcvtand the torqueratio ?sare given in figure 5.For instationary situations, Ides model states that the rate of ratio change rcvtis a functionof the ratio rcvt, primary pulley speed p, clamping forces Fpand Fsand torque ratio ?s: rcvt= kr(rcvt) |p|Fshift;Fshift= Fp (rcvt,?s) Fs(10)An axial force difference Fshift, weighted by the thrust ratio results in a ratio change, and istherefore called the shift force.The occurrence of pin the model (10) is plausible because anincreasing shift force is needed for decreasing pulley speeds to obtain the same rate of ratiochange. The reason is that less V-shaped blocks enter the pulleys per second when the pulleyspeed decreases. As a result the radial belt travel per revolution of the pulleys must increaseand this requires a higher shift force. However, it is far from obvious that the rate of ratiochange is proportional to both the shift force and the primary pulley speed. kris a non-linearfunction of the ratio rcvtand has been obtained experimentally. Experimental data has beenused to obtain a piecewise linear fit, which are depicted in figure6. The estimation of krhas392M. Pesgens et al.Figure 5.Contour plot of (rcvt,?s).Figure 6.Fit of kr(rcvt); greyed-out dots correspond to data with reduced accuracy.Hydraulically actuated CVT393Figure 7.Comparison of shifting speed, Ides model vs. measurement.been obtained using the inverse Ide model:kr(rcvt) = rcvt|p|Fshift(11)In the denominator Fshiftis present, the value of which can become (close to) zero. Obviously,the estimate is very sensitive for errors in Fshiftwhen its value is small. The dominant dis-turbances in Fshiftare caused by high-frequency pump generated pressure oscillations, whichdo not affect the ratio (due to the low-pass frequency behavior of unmodeled variator pulleyinertias). The standard deviation of the pressure oscillations and other high-frequency distur-bances has been determined applying a high-pass Butterworth filter to the data of Fshift. Toavoid high-frequency disturbances in Fshiftblurring the estimate of kr, estimates for values ofFshiftsmaller than at least three times the disturbances standard deviation have been ignored(these have been plotted as grey dots in figure6), whereas the other points have been plottedas black dots.The white line is the resulting fit of this data.The few points with negative valuefor krhave been identified as local errors in the map of .To validate the quality of Ides model, the shifting speed rcvt, recorded during a road exper-iment, is compared with the same signal predicted using the model. Model inputs are thehydraulic pulley pressures (pp, ps) and pulley speeds (p, s) together with the estimatedprimary pulley torque (Tp). The result is depicted in figure7. The model describes the shiftingspeed well, but for some upshifts it predicts too large values. This happens only for high CVTratios, i.e. rcvt 1.2, where the data of is unreliable due to extrapolation (see figure5).3.The hydraulic systemThe hydraulic part of the CVT (see figure3) consists of a roller vane pump directly connectedto the engine shaft, two solenoid valves and a pressure cylinder on each of the moving pulley394M. Pesgens et al.sheaves. The volume between the pump and the two valves including the secondary pulleycylinder is referred to as the secondary circuit, the volume directly connected to and includingthe primary pulley cylinder is the primary circuit. Excessive flow in the secondary circuitbleeds off toward the accessories, whereas the primary circuit can blow off toward the drain.All pressures are gage pressures, defined relative to the atmospheric pressure. The drain is atatmospheric pressure.The clamping forces Fpand Fsare realized mainly by the hydraulic cylinders on the move-ablesheavesanddependonthepressuresppandps.Asthecylindersareanintegralpartofthepulleys, they rotate with an often very high speed, so centrifugal effects have to be taken intoaccount and the pressure in the cylinders will not be homogeneous. Therefore, the clampingforceswillalsodependonthepulleyspeedspands.Furthermore,apreloadedlinearelasticspring with stiffness kspris attached to the moveable secondary sheave. This spring has toguarantee a minimal clamping force when the hydraulic system fails. Together this results inthe following relations for the clamping forces:Fp= Appp+ cp2p(12)Fs= Asps+ cs2s ksprss+ F0(13)where cpand csare constants, whereas F0is the spring force when the secondary moveablesheave is at position ss= 0. Furthermore, Apand Asare the pressurized piston surfaces. Inthe hydraulic system of figure3, the primary pressure is smaller than the secondary pressure ifthereisanoilflowfromthesecondarytotheprimarycircuit.Therefore,toguaranteethatinanycase the primary clamping force can be up to twice as large as the secondary clamping force,the primary piston surface Apis approximately twice as large as the secondary surface As.Itisassumedthattheprimaryandthesecondarycircuitarealwaysfilledwithoilofconstanttemperature and a constant air fraction of 1%. The volume of circuit ( = p, s) is given by:V= V,min+ As(14)V,minis the volume if s= 0 and Ais the pressurized piston surface.The law of mass conservation, applied to the primary circuit, combined with equation(14),results in:oilVp pp= Qsp Qpd Qp,leak Qp,V(15)Qspis the oil flow from the secondary to the primary circuit, Qpdis the oil flow from theprimary circuit to the drain, Qp,leakis the (relatively small) oil flow leaking through narrowgaps from the primary circuit and Qp,Vis the oil flow due to a change in the primary pulleycylinder volume. Furthermore, oilis the compressibility of oil. The oil flow Qspis given by:Qsp= cfAsp(xp) ?2|ps pp|sign(ps pp)(16)wherecfisaconstantflowcoefficientand istheoildensity.Asp,theequivalentvalveopeningareaforthisflowpath,dependsontheprimaryvalvestempositionxp.FlowQpdfollowsfrom:Qpd= cfApd(xp) ?2pp(17)Here, Apdis the equivalent opening area of the primary valve for the flow from primary circuittothedrain.TheconstructionofthevalveimpliesthatAsp(xp) Apd(xp) = 0forallpossiblexp.Hydraulically actuated CVT395Flow Qp,leakis assumed to be laminar with leak flow coefficient cpl, so:Qp,leak= cplpp(18)The flow due to a change of the primary pulley cylinder volume is described by:Qp,V= Ap sp(19)with spgiven by equation (4).Application of the law of mass conservation to the secondary circuit yieldsoilVsps= Qpump Qsp Qsa Qs,leak Qs,V(20)The flow Qpump, generated by the roller vane pump, depends on the angular speed eof theengine shaft, on the pump mode m (m = SS for single sided and m = DS for double sidedmode), and the pressure psat the pump outlet, so Qpump= Qpump(e,ps,m). Qsais the flowfrom the secondary circuit to the accessories and Qs,leakis the leakage from the secondarycircuit. Flow Qsais modeled as:Qsa= cfAsa(xs) ?2|ps pa|sign(ps pa)(21)where Asa, the equivalent valve opening of the secondary valve, depends on the valve stemposition xs. The laminar leakage flow Qs,leakis given by (with flow coefficient csl):Qs,leak= cslps(22)The flow due to a change of the secondary pulley cylinder volume is:Qs,V= As ss(23)with ssaccording to equation(3).The accessory circuit contains several passive valves. In practice, the secondary pressurepswill always be larger than the accessory pressure pa, i.e. no backflow occurs. The relationbetween paand psis approximately linear, sopa= ca0+ ca1ps(24)with constants ca0 0 and ca1 (0,1).NowthatacompletemodelofthepushbeltCVTanditshydraulicsisavailable,thecontrollerand its operational constraints can be derived.4.The constraintsThe CVT ratio controller (in fact) controls the primary and secondary pressures. Severalpressure constraints have to be taken into account by this controller:1. the torque constraints p p,torqueto prevent slip on the pulleys;2. the lower pressure constraints p p,lowto keep both circuits filled with oil. Here, fairlyarbitrary, pp,low= 3 bar is chosen. To enable a sufficient oil flow Qsato the accessorycircuit, and for a proper operation of the passive valves in this circuit it is necessary that396M. Pesgens et al.Qsais greater than a minimum flow Qsa,min. A minimum pressure ps,lowof 4 bar turnsout to be sufficient;3. the upper pressure constraints p p,max, to prevent damage to the hydraulic lines,cylinders and pistons. Hence, pp,max= 25 bar, ps,max= 50 bar;4. thehydraulicconstraintsp p,hydtoguaranteethattheprimarycircuitcanbleedofffastenough toward the drain and that the secondary circuit can supply sufficient flow towardthe primary circuit.The pressures pp,torqueand ps,torquein constraint 1 depend on the critical clamping forceFcrit, equation(5). The estimated torqueTpis calculated using the stationary engine torquemap, torque converter characteristics and lock-up clutch mode, together with inertia effects ofthe engine, flywheel and primary gearbox shaft. A safety factor ks= 0.3 with respect to theestimated maximal primary torqueTp,maxhas been introduced to account for disturbances onthe estimated torqueTp, such as shock loads at the wheels. Then the pulley clamping force(equal for both pulleys, neglecting the variator efficiency) needed for torque transmissionbecomes:Ftorque=cos() (|Tp|+ ksTp,max)2 Rp(25)Consequently, the resulting pressures can be easily derived using equations(12) and (13):pp,torque=1Ap?Ftorque cp2p?(26)ps,torque=1As?Ftorque cs2s ksprss F0?(27)Exactly the same clamping strategy has been previously used by ref. 3 during test standefficiency measurements of this gearbox and test vehicle road tests. No slip has been reportedduringanyofthoseexperiments.Asthemaingoalofthisworkistoanimprovedratiotrackingbehavior, the clamping strategy has remained unchanged.A further elaboration of constraints 4 is based on the law of mass conservation for theprimary circuit. First of all, it is noted that for this elaboration the leakage flow Qp,leakandthe compressibility term oilVp ppmay be neglected because they are small compared tothe other terms. Furthermore, it is mentioned again that the flows Qspand Qpdcan never beunequal to zero at the same time. Finally, it is chosen to replace the rate of ratio change rcvtby the desired rate of ratio shift rcvt,d, that is specified by the hierarchical driveline controller.If rcvt,d 0 andQsp= 0. Constraint 4 with respect to the primary pulley circuit then results in the followingrelation for the pressure pp,hyd:pp,hyd=oil2?Appmax(0, rcvt,d)cfApd,max?2(28)where Apd,maxis the maximum opening of the primary valve in the flow path from the primarycylinder to the drain.In a similar way, a relation for the secondary pulley circuit pressure ps,hydin constraint 4can be derived. This constraint is especially relevant if rcvt 0, i.e. if the flow Qspfrom thesecondary to the primary circuit has to be positive and, as a consequence, Qpd= 0. This thenHydraulically actuated CVT397results in:ps,hyd= pp,d+oil2?Appmax(0, rcvt,d)cfAsp,max?2(29)whereAsp,maxisthemaximumopeningoftheprimaryvalveintheflowpathfromthesecondaryto the primary circuit.For the design of the CVT ratio controller it is advantageous to reformulate to constraintsin terms of clamping forces instead of pressures. Associating a clamping force F,with thepressure p,and using equations (12) and (13) this results in the requirement:F,min F F,max(30)with minimum pulley clamping forces:F,min= max(F,low,F,torque,F,hyd)(31)5.Control designItisassumedinthissectionthatateachpointoftimet,theprimaryspeedp(t),theratiorcvt(t),the primary pressure pp(t) and the secondary pressure ps(t) are known from measurements,filtering and/or reconstruction. Furthermore, it is assumed that the CVT is mounted in avehicular driveline and that the desired CVT ratio rcvt,d(t) and the desired rate of ratio change rcvt,d(t)arespecifiedbytheoverallhierarchicaldrivelinecontroller.Thisimplies,forinstance,that at each point of time the constraint forces can be determined.The main goal of the local CVT controller is to achieve fast and accurate tracking of thedesired ratio trajectory. Furthermore, the controller should also be robust for disturbances.Animportant subgoal is to maximize the efficiency. It is quite plausible (and otherwise supportedby experiments, 3) that to realize this sub-goal the clamping forces Fpand Fshave to be assmall as possible, taking the requirements in equation(30) into account.Theoutputoftheratiocontrollerissubjecttotheconstraintsofequation(31).TheconstraintsF F,mincan effectively raise the clamping force setpoint of one pulley, resulting in anundesirable ratio change. This can be counteracted by raising the opposite pulleys clampingforceaswell,usingmodel-basedcompensatortermsintheratiocontroller.UsingIdesmodel,i.e. using equation(10), expressions for the ratio change forces Fp,ratioand Fs,ratio(figure8)can be easily derived:Fp,ratio= Fshift,d+ Fs,min(32)Fs,ratio=Fshift,d+ Fp,min(33)where Fshift,dis the desired shifting force, basically a weighted force difference betweenboth pulleys. As explained earlier, depends on ?s, which in turn depends on Fs. This is animplicitrelation(Fs,ratiodependsonFs),whichhasbeentackledbycalculating frompressuremeasurements.It will now be shown that at each time, one of the two clamping forces is equal to F,min,whereastheotherdeterminestheratio.Usingequations(30),(32)and(33)thedesiredprimary398M. Pesgens et al.Figure 8.Ratio controller with constraints compensationand secondary clamping forces Fp,dand Fs,dare given by:Fp,d= Fp,ratioFs,d= Fs,min?if Fshift,d+ Fs,min Fp,min(34)Fp,d= Fp,minFs,d= Fs,ratio?if Fshift,d+ Fs,min Fp,minFp,min Fs,ratio= Fshift,dif Fshift,d+ Fs,min Fp,max Fs,ratio Fs,max(40)If either pressure saturates (pp= pp,maxor ps= ps,max), the shifting speed error inevitablybecomes large. The anti-windup algorithm ensures stability, but the tracking behavior willdeteriorate. This is a hardware limitation which can only be tackled by enhancing the variatorand hydraulics hardware. The advantage of a conditional anti-windup vs. a standard (linear)algorithm is that the linear approach requires tuning for good performance, whereas the con-ditionalapproachdoesnot.Furthermore,theperformanceoftheconditionalalgorithmcloselyresembles that of a well-tuned linear mechanism.6.Experimental resultsAs the CVT is already implemented in a test vehicle, in-vehicle experiments on a rollerbench have been performed to tune and validate the new ratio controller. To prevent a non-synchronizedoperationofthrottleandCVTratio,theacceleratorpedalsignal(seefigure1)hasbeenusedastheinputforthevalidationexperiments.Thecoordinatedcontrollerwilltrackthemaximum engine efficiency operating points.A semi kick-down action at a cruise-controlledspeedof50km/hfollowedbyapedalbackouthasbeenperformedinasinglereferenceexper-iment. The recorded pedal angle (see figure9) has been applied to the coordinated controller.This approach cancels the limited human drivers repeatability.The upper plot of figure10 shows the CVT ratio response calculated from speed measure-ments using equation(1), the plot depicts the tracking error. As this is a quite demandingexperiment, the tracking is still adequate. Much better tracking performance can be obtainedwith more smooth setpoints, but the characteristics of the responses will become less distinctas well. Figure11 shows the primary and secondary pulley pressures. The initial main peakin the error signal (around t = 1.5 s) is caused by saturation of the secondary pressure (lowerplot of figure11), due to a pump flow limitation. If a faster initial response were required,adaptation of the hydraulics hardware would be necessary.After the initial fast downshift, theratio reaches its setpoint (around t = 7 s) before downshifting again. All changes in shifting400M. Pesgens et al.Figure 9.Pedal input for the CVT powertrain.direction (t = 1.3, t = 1.6 and t = 7.5 s) occur with a relatively small amount of overshoot,which shows that the integrator anti-windup algorithm performs well.Looking at the primary pressure in the vicinity of t = 1.5 s, it can be observed that thispressure peaks repeatedly above its setpoint. This behavior is caused by performance limi-tations of the primary pressure controller. The developed controller guarantees that only onepulley pressure setpoint at the time is raised above its lower constraint, and only to realizeFigure 10.CVT ratio response and tracking error, roller bench semi-kickdown.Hydraulically actuated CVT401Figure 11.Primary and secondary pulley pressures, roller bench semi-kickdown.a desired ratio. This is visualized in figure12. Higher clamping forces cause more losses inthe CVT 10, as long as no macro-slip occurs. The main causes are oil pump power demand(approximately linear with pressure) and losses in the belt itself, which both increase withincreasing clamping pressure, as supported by measurements 16. Hence, this controller hasa potential for improving the efficiency of a CVT, compared to non-model based controllers.Figure 12.New controllers pulley pressure setpoints minus lower constraints.402M. Pesgens et al.Looking back to the lower plot of figure10, the second (positive) peak (after the firstnegative peak due to actuator saturation) represents the overshoot of the ratio response due toa shifting direction change. This quantity describes the tracking performance of a controllerwell, and will be used to evaluate a controllers performance. The overshoot is computed hereas the (positive) maximum of the ratio error: max(rcvt,d rcvt).Also, the mean absolute error(1/N)?N0|rcvt,d rcvt| (for the N data points in the 10 s response) will be used to compareresults.The same experiment has been performed for several variations on the controller. For eachof these variations, all constraints are still imposed, but some of the compensator terms in theratiocontrollerhavebeentemporarilyswitchedoff(theverticalarrowsinfigure8).Theresultshave been compared with the results for the total controller and are depicted in figure13. Thecases that will be addressed are:1. All feedforwards and compensators on (total).2. No setpoint feedforward (setp ff off), rcvt,d= 0 in equation(37).3. No critical (no belt slip) torque constraint compensation (T comp off), Ftorque= 0.4. No hydraulic constraints compensation (hydr comp off), F,hyd= 0.5. No torque transmission nor hydraulic constraints compensation (T,hydr comp off),Ftorque= 0, F,hyd= 0.It is immediately clear that of all alternatives, the total controller with all feedforwards andcompensators on (total) described in the previous paragraph performs best, implying that allcontrollertermshaveapositivecontributiontowardsminimizingthetrackingerror.Switchingoff either the hydraulic constraints compensation terms (hydr comp off) or the torque trans-mission compensator (T comp off) does not severely degrade the tracking quality. However,switchingbothcompensatorsoff(T,hydrcompoff)doesintroducelargetrackingerrors.Thisoccurs because the maximum operator of both constraints is taken to calculate the compen-sating action, and if one constraint compensator is zero, the output of the maximum operatorFigure 13.Overshoot and mean absolute error for several controller alternatives.Hydraulically actuated CVT403will still be non-zero due to the second constraint. Both compensators switched off simulta-neously effectively introduce a dead zone in the controller output u, the result of which isobvious. The response with the setpoint feedforward switched off (setp ff off) increases theerrors due to increased phase lag of the resulting response. The obtained results of the totaldeveloped controller show better tracking behavior (overshoot and mean absolute error) andlower transient pulley pressures (only during ratio change, as the clamping strategy is equal)compared with results obtained with a previously adopted controller, as described in ref. 3.This could be an indication for the potential for improving the CVT efficiency of the newcontroller, as described before.Vehicletestsincludingtipshifting(featuringstepwiseratiosetpointchanges)havebeenper-formed on a test track, see figure 14.The stepwise changes in the ratio setpoint are trajectoriesthat cannot be realized. Hence, the measured CVT ratio will always lag behind. Hence, thisexperiment demonstrates the robustness against actuator saturation, as the pressure of the pul-ley that controls the ratio will saturate.As the errors in the feedforward terms of the controllerwill increase, the feedback controller becomes increasingly important. Also the anti-windupmechanismoftheratiocontrollerneedstopreventovershoot.Resultsofanexperimentdrivingat a cruise-controlled speed of 50 km/h are depicted in figures15 and 16. A new gear ratiosetpoint is generated every 2 s.At the start of the up-shift ratio responses at t = 2.1 s and t = 4.2 s, an inverse response ispresent.As the shifting speeds are indeed very high in this experiment, because of the layoutof the hydraulic system, the secondary circuit needs to supply the primary circuit with oil.Asa result, the secondary pressure rises in advance to the primary pressure and causes an initialdownshift. Around t = 3 s and t = 5 s, the ratio initially rises approximately linear, causedby the limited pump flow as the oil pump runs at engine speed, which is low. Upshifting isfurther characterized by some overshoot, which is clearly visible at t = 14 s. As the primarypressurecannotdropsufficientlyquickduetoalimitedprimaryvalveflow-throughareatowardthe drain, upshifting continues and causes overshoot. The secondary pressure only saturatesbriefly due to the limited pump flow after each ratio setpoint change. Much less overshoot ispresent during a downshift, the speed of which is not limited by pump flow.Again the primarypressure peaks above its setpoint when the secondary pressure is increased rapidly, causedFigure 14.Experimental vehicle during tip-shifts at the test track.404M. Pesgens et al.Figure 15.CVT ratio response and tracking error, road tip shifting.by limitations in the primary pressure controller. This phenomenon lowers the maximumdownshift speed and is visible as a slight bumpin the ratio at t = 6.2 s and t = 8.2 s.As the main goal of the presented experiments is to demonstrate a new ratio controllerconcept, during the experiments belt slip has been avoided using a proven clamping strategyas mentioned earlier. Also, an online model-based detection algorithm was used, verifyingthat |?s| 1. Two methods to detect belt slip off-line from measurement data (without directFigure 16.Primary and secondary pulley pressures, road tip shifting.Hydraulically actuated CVT405measurements of the belts running radius on the pulleys to calculate the so-called geometricratio) have been used after the experiments. First, it has been verified if the range of CVTratios geometrically possible is not exceeded (rLOW rcvt rOD). Secondly, the maximumshifting speed of the CVT is limited due to limited clamping forces and variator speed, seeequation(10). The coefficient of friction in the excessive (macro-) slip region of a push-beltdecreases with slip speed 8. This causes unstable dynamic behavior, and hence slip speedwillincreaserapidlywhenthetorquecapacityofaV-beltisexceeded.Astheratioiscalculatedfrom measured pulley speeds, excessively fast ratio changes (high values of rcvt) can indicatebelt slip. The results of each measurement have been scrutinized, the result of which did notshow any traces of belt slip effects.7.ConclusionsA new ratio controller for a metal push-belt CVT with a hydraulic belt clamping system hasbeen developed. On the basis of dynamic models of the variator and hydraulics, compensatorterms of system constraints, a setpoint feedforward and a linearizing feedback controller havebeen implemented. The feedback controller is a PID controller wi

温馨提示:
1: 本站所有资源如无特殊说明，都需要本地电脑安装OFFICE2007和PDF阅读器。图纸软件为CAD,CAXA,PROE,UG,SolidWorks等.压缩文件请下载最新的WinRAR软件解压。
2: 本站的文档不包含任何第三方提供的附件图纸等，如果需要附件，请联系上传者。文件的所有权益归上传用户所有。
3.本站RAR压缩包中若带图纸，网页内容里面会有图纸预览，若没有图纸预览就没有图纸。
4. 未经权益所有人同意不得将文件中的内容挪作商业或盈利用途。
5. 人人文库网仅提供信息存储空间，仅对用户上传内容的表现方式做保护处理，对用户上传分享的文档内容本身不做任何修改或编辑，并不能对任何下载内容负责。
6. 下载文件中如有侵权或不适当内容，请与我们联系，我们立即纠正。
7. 本站不保证下载资源的准确性、安全性和完整性, 同时也不承担用户因使用这些下载资源对自己和他人造成任何形式的伤害或损失。

人人文库网所有资源均是用户自行上传分享，仅供网友学习交流，未经上传用户书面授权，请勿作他用。