首页 人人文库网 > 图纸下载 > 毕业设计 > 接线端子板的冲孔、落料、压弯复合模设计【优秀】【word+10张CAD图纸全套】【冲压复合模类】【毕设】
表格.doc

接线端子板的冲孔、落料、压弯复合模设计【优秀】【word+10张CAD图纸全套】【冲压复合模类】【毕设】

收藏

压缩包内文档预览：
预览图 预览图 预览图 预览图 预览图 预览图 预览图 预览图 预览图
编号：298491    类型：共享资源    大小：1.05MB    格式：RAR    上传时间：2014-07-23 上传人：QQ14****9609 IP属地：陕西
45
积分
举报
举报 版权申诉
版权申诉 word格式文档无特别注明外均可编辑修改；预览文档经过压缩，下载后原文更清晰！ 立即下载
关 键 词：
接线 端子 冲孔 落料 复合 设计 优秀 优良 word 10 cad 图纸 全套 冲压
资源描述：

接线端子板的冲孔、落料、压弯复合模设计【优秀】【word+10张CAD图纸全套】【冲压复合膜类】【毕业设计】

【外文翻译】【64页@正文28600字】【详情如下】【需要咨询购买全套设计请加QQ1459919609】

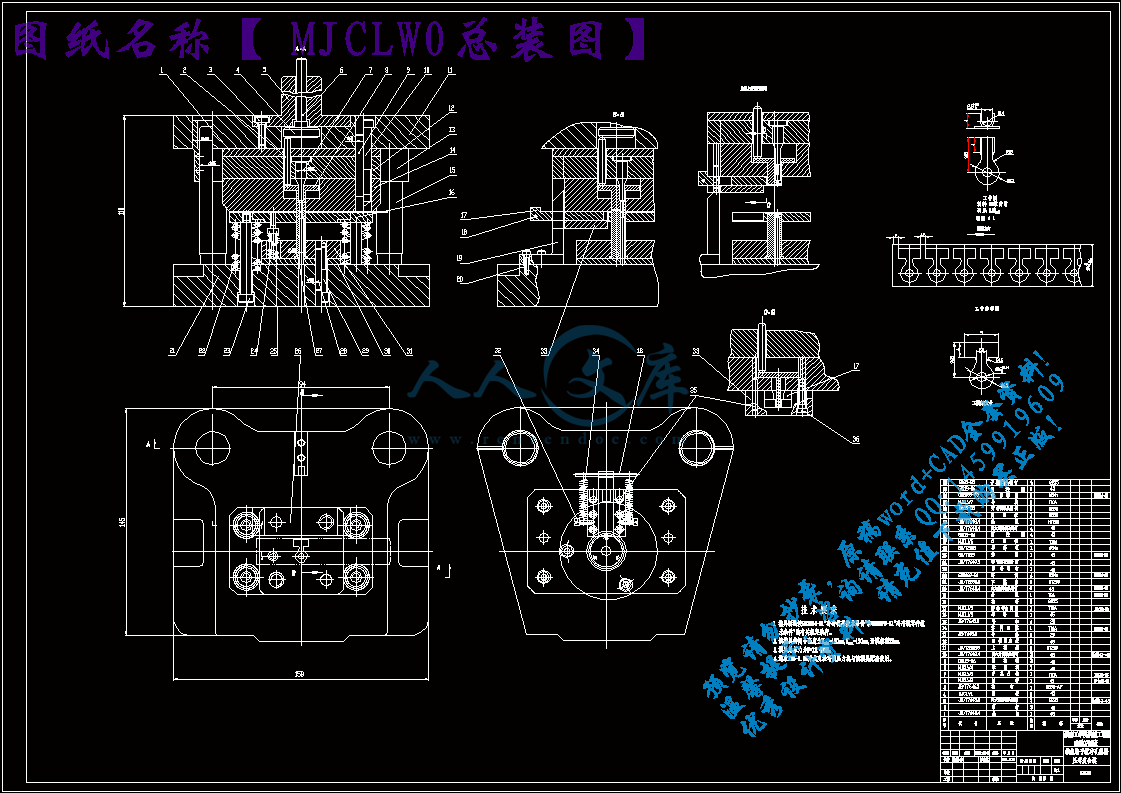
MJCLW0总装图.dwg

MJCLW1推板.dwg

MJCLW2打杆.dwg

MJCLW3冲孔凸模.dwg

MJCLW4推件块.dwg

MJCLW5活动弯曲凹模.dwg

MJCLW6凸凹模.dwg

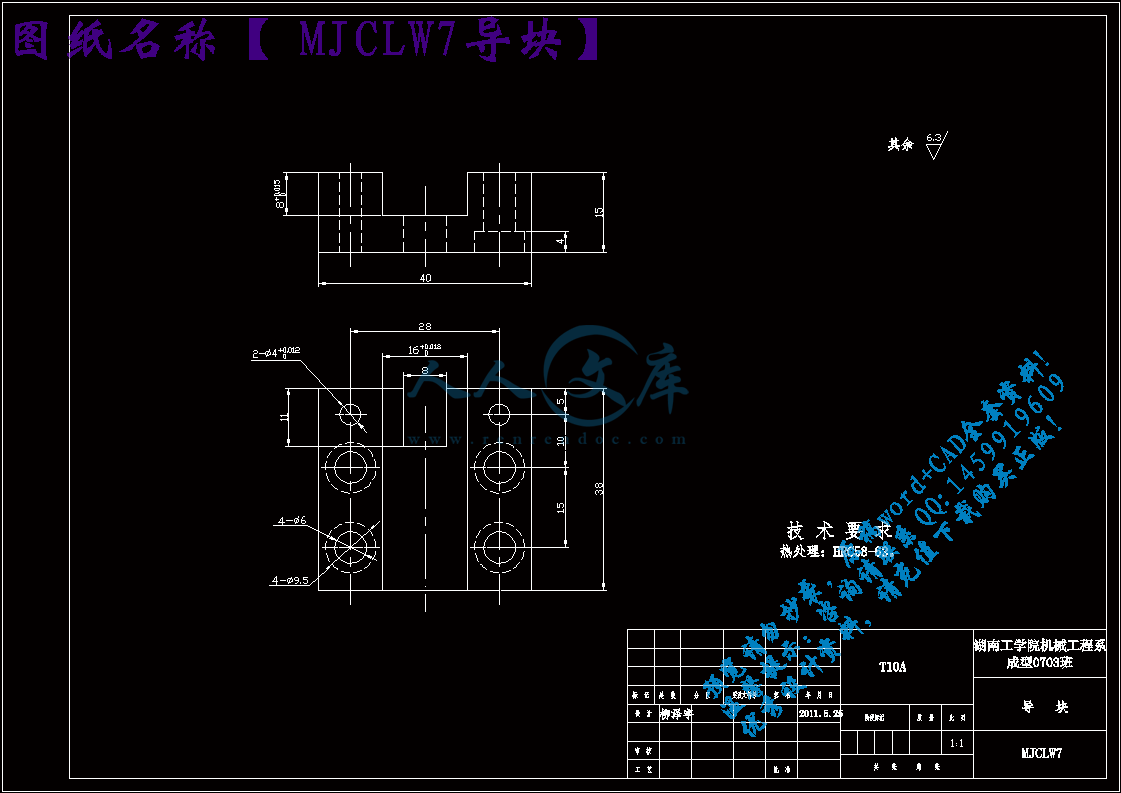
MJCLW7导块.dwg

MJCLW8工件图.dwg

MJCLW9卸料板.dwg

外文原文.pdf

正文.doc

英文翻译.doc

表格.doc

摘 要：阐述了冲孔、落料、压弯复合模的结构设计及工作原理。通过工艺分析，在冲压材料厚度较薄的小型弯曲件时，采用冲孔、落料、弯曲复合模比采用连续或级进模简单。通过冲裁力、顶件力、卸料力等计算，确定模具类型。该模具采用后侧导柱模架结构形式。废料从凸凹模和下底座中所开的槽中排出。本模具性能可靠，运行平稳，能够适应大批量生产要求，提高了产品质量和生产效率，降低劳动强度和生产成本。

关键字：冲压；冲孔、落料、弯曲；复合模

ABSTRACT                                    

Abstract: Expounded punching, blanking, bending modulus of the composite structure design and principle. Process analysis by the stamping of thinner material thickness small curved pieces, will use the punching, blanking, flexural modulus composites than continuous or Progressive Die simple. Punching through, the top pieces, such as the discharge of calculation to determine the type mold. The posterior mold using derivative-scale structures form. Waste from the punch and die and the base under which opened the tank discharges. The mold reliable, stable operation to adapt to the requirements of large-scale production, improve product quality and production efficiency. reduce labor intensity and the cost of production.

Keywords: Ramming; The punch holes, Fall the material curving; Superposable die

目   录

第一章  绪  论1

1.1、冷冲压与模具设计简介1

1.2、我国冲压模具水平状况1

1.3、冲压模具的发展重点与展望4

1.4、本次设计的意义6

第二章 冲压件工艺性分析及冲裁方案的确定7

2.1冲裁件的结构工艺性7

2.2冲裁件尺寸精度和表面粗糙度要求9

2.3冲裁件的尺寸基准9

2.4 冲裁件经济性分析10

2.5冲裁方案的确定10

第三章 排样图的设计及材料利用率的计算12

3.1排样的设计12

3.2搭边的选取14

3.3材料利用率的计算15

第四章 冲裁工艺力的计算17

4.1冲裁力的计算17

4.1.1冲压力的行程曲线17

4.1.2冲裁力的计算公式18

4.1.3降低冲裁力的方法18

4.2卸料力、推件力、和弯曲力等其他力的计算19

4．3冲压压力中心21

第五章  冲压设备的选择24

5.1冲压设备类型的选择24

5.2确定设备的规格24

第六章 冲裁模工作部分设计计算27

6.1冲裁间隙27

6.1.1对冲裁件质量的影响27

6.1.2 对模具寿命的影响28

6.1.3 对冲裁力、卸料力的影响29

6.2合理间隙的选用30

6.3 模具刃口尺寸的计算32

第七章 模具总体设计39

7.1模具类型的选择39

7.2确定送料方式39

7.3定位方式的选择39

7.4卸料、出件方式的选择39

7.5导向方式的选择39

第八章  主要零部件设计41

8.1模具材料的选择41

8.1.1模具材料与热处理41

8.1.2 H62软黄铜的性能41

8.2落料凹模设计42

8.2.1落料凹模刃口形式42

8.2.2落料凹模外形和尺寸的确定42

8.3凸、凹模设计43

8.3.1模具的结构形式和固定方法43

8.3.2凸凹模长度的确定44

8.3.3凸凹模结构设计44

8.4冲孔凸模45

8.4.1冲孔凸模的固定形式45

8.4.2冲孔凸模长度的确定45

8.4.3凸模强度校核45

8.4.4 冲孔凸模的结构47

8.5卸料弹簧的选择47

8.6 打杆的选择48

8.7 活动弯曲凹模的设计49

第九章 标准件的选择50

9.1模架及模柄的选择50

9.2凸模固定板及垫板的选择50

9.3 导尺的选择51

9.4模具闭合高度的校核51

9.6推杆的选择52

9.7螺钉及销钉的选择52

第十章 总装图的设计及绘制54

结     论55

参考文献56

致     谢57

附    录58

第一章  绪  论

1.1、冷冲压与模具设计简介

我国冲压模具无论在数量上，还是在质量、技术和能力等方面都已有了很大发展，但与国民经济需求和世界先进水平相比，差距仍很大，一些大型、精密、复杂、长寿命的高档模具每年仍大量进口，特别是中高档轿车的覆盖件模具，目前仍主要依靠进口。一些低档次的简单冲模，已趋供过于求，市场竞争激烈。

据中国模具工业协会发布的统计材料，2004年我国冲压模具总产出约为220亿元，其中出口0.75亿美元，约合6.2亿元。

根据我国海关统计资料，2004年我国共进口冲压模具5.61亿美元，约合46.6亿元。从上述数字可以得出2004年我国冲压模具市场总规模约为266.6亿元。其中国内市场总需求为260.4亿元，总供应约为213.8亿元，市场满足率为82%。在上述供求总体情况中，有几个具体情况必须说明：一是进口模具大部分是技术含量高的大型精密模具，而出口模具大部分是技术含量较低的中低档模具，因此技术含量高的中高档模具市场满足率低于冲压模具总体满足率，这些模具的发展已滞后于冲压件生产，而技术含量低的中低档模具市场满足率要高于冲压模具市场总体满足率；二是由于我国的模具价格要比国际市场低格低许多，具有一定的竞争力，因此其在国际市场的前景看好，2005年冲压模具出口达到1.46亿美元，比2004年增长94.7%就可说明这一点；三是近年来港资、台资、外资企业在我国发展迅速，这些企业中大量的自产自用的冲压模具无确切的统计资料，因此未能计入上述数字之中。

1.2、我国冲压模具水平状况

近年来，我国冲压模具水平已有很大提高。大型冲压模具已能生产单套重量达50多吨的模具。为中档轿车配套的覆盖件模具国内也能生产了。精度达到1～2μm，寿命2亿次左右的多工位级进模国内已有多家企业能够生产。表面粗糙度达到Ra≦1.5μm的精冲模，大尺寸（Φ≧300mm）精冲模及中厚板精冲模国内也已达到相当高的水平。

1.模具CAD/CAM技术状况

我国模具CAD/CAM技术的发展已有20多年历史。由原华中工学院和武汉733厂于1984年共同完成的精冲模CAD/CAM系统是我国第一个自行开发的模具CAD/CAM系统。由华中工学院和北京模具厂等于1986年共同完成的冷冲模CAD/CAM系统是我国自行开发的第一个冲裁模CAD/CAM系统。上海交通大学开发的冷冲模CAD/CAM系统也于同年完成。20世纪90年代以来，国内汽车行业的模具设计制造中开始采用CAD/CAM技术。国家科委863计划将东风汽车公司作为CIMS应用示范工厂，由华中理工大学作为技术依托单位，开发的汽车车身与覆盖件模具CAD/CAPP/CAM集成系统于1996年初通过鉴定。

在此期间，一汽和成飞汽车模具中心引进了工作站和CAD/CAM软件系统，并在模具设计制造中实际应用，取得了显著效益。1997年一汽引进了板料成型过程计算机模拟CAE软件并开始用于生产。

21世纪开始CAD/CAM技术逐渐普及，现在具有一定生产能力的冲压模具企业基本都有了CAD/CAM技术。其中部分骨干重点企业还具备各CAE能力。

模具CAD/CAM技术能显著缩短模具设计与制造周期，降低生产成本，提高产品质量，已成为人们的共识。在“八五”、“九五”期间，已有一大批模具企业推广普及了计算机绘图技术，数控加工的使用率也越来越高，并陆续引进了相当数量的CAD/CAM系统。如美国EDS的UG，美国ParametricTechnology公司的Pro/Engineer，美国CV公司的CADS5，英国DELCAM公司的DOCT5，日本HZS公司的CRADE及space-E，以色列公司的Cimatron，还引进了AutoCAD、CATIA等软件及法国Marta-Daravision公司用于汽车及覆盖件模具的Euclid-IS等专用软件。国内汽车覆盖件模具生产企业普遍采用了CAD/CAM技术。DL图的设计和模具结构图的设计均已实现二维CAD，多数企业已经向三维过渡，总图生产逐步代替零件图生产。且模具的参数化设计也开始走向少数模具厂家技术开发的领域。

在冲压成型CAE软件方面，除了引进的软件外，华中科技大学、吉林大学、湖南大学等都已研发了较高水平的具有自主知识产权的软件，并已在生产实践中得到成功应用，产生了良好的效益。

快速原型(RP)与传统的快速经济模具相结合，快速制造大型汽车覆盖件模具，解决了原来低熔点合金模具靠样件浇铸模具，模具精度低、制件精度低，样件制作难等问题，实现了以三维CAD模型作为制模依据的快速模具制造，并且保证了制件的精度，为汽车行业新车型的开发、车身快速试制提供了覆盖件制作的保证，它标志着RPM应用于汽车车身大型覆盖件试制模具已取得了成功。

围绕着汽车车身试制、大型覆盖件模具的快速制造，近年来也涌现出一些新的快速成型方法，例如目前已开始在生产中应用的无模多点成型及激光冲击和电磁成型等技术。它们都表现出了降低成本、提高效率等优点。

2.模具设计与制造能力状况

在国家产业政策的正确引导下，经过几十年努力，现在我国冲压模具的设计与制造能力已达到较高水平，包括信息工程和虚拟技术等许多现代设计制造技术已在很多模具企业得到应用。

虽然如此，我国的冲压模具设计制造能力与市场需要和国际先进水平相比仍有较大差距。这些主要表现在高档轿车和大中型汽车覆盖件模具及高精度冲模方面，无论在设计还是加工工艺和能力方面，都有较大差距。轿车覆盖件模具，具有设计和制造难度大，质量和精度要求高的特点，可代表覆盖件模具的水平。虽然在设计制造方法和手段方面已基本达到了国际水平，模具结构功能方面也接近国际水平，在轿车模具国产化进程中前进了一大步，但在制造质量、精度、制造周期等方面，与国外相比还存在一定的差距。

标志冲模技术先进水平的多工位级进模和多功能模具，是我国重点发展的精密模具品种。有代表性的是集机电一体化的铁芯精密自动阀片多功能模具，已基本达到国际水平。

 但总体上和国外多工位级进模相比，在制造精度、使用寿命、模具结构和功能上，仍存在一定差距。

汽车覆盖件模具制造技术正在不断地提高和完善，高精度、高效益加工设备的使用越来越广泛。高性能的五轴高速铣床和三轴的高速铣床的应用已越来越多。NC、DNC技术的应用越来越成熟，可以进行倾角加工和超精加工。这些都提高了模具型面加工精度，提高了模具的质量，缩短了模具的制造周期。

  模具表面强化技术也得到广泛应用。工艺成熟、无污染、成本适中的离子渗氮技术越来越被认可，碳化物被覆处理（TD处理）及许多镀（涂）层技术在冲压模具上的应用日益增多。真空处理技术、实型铸造技术、刃口堆焊技术等日趋成熟。激光切割和激光焊接技术也得到了应用。

3.专业化程度及分布状况

我国模具行业专业化程度还比较低，模具自产自配比例过高。国外模具自产自配比例一般为30%，我国冲压模具自产自配比例为60%。这就对专业化产生了很多不利影响。现在，技术要求高、投入大的模具，其专业化程度较高，例如覆盖件模具、多工位级进模和精冲模等。而一般冲模专业化程度就较低。由于自配比例高，所以冲压模具生产能力的分布基本上跟随冲压件生产能力的分布。但是专业化程度较高的汽车覆盖件模具和多工位、多功能精密冲模的专业生产企业的分布有不少并不跟随冲压件能力分布而分布，而往往取决于主要投资者的决策。例如四川有较大的汽车覆盖件模具的能力，江苏有较强的精密冲模的能力，而模具的用户大都不在本地。


1.3、冲压模具的发展重点与展望

发展重点的选取应根据市场需求、发展趋势和目前状况来确定。可按产品重点、技术重点和其他重点分别叙述。

1、冲压模具产品发展重点。

冲压模具共有7小类，并有一些按其服务对象来称呼的一些种类。目前急需发展的是汽车覆盖件模具，多功能、多工位级进模和精冲模。这些模具现在产需矛盾大，发展前景好。

汽车覆盖件模具中发展重点是技术要求高的中高档轿车大中型覆盖件模具，尤其是外覆盖件模具。高强度板和不等厚板的冲压模具及大型多工位级进模、连续模今后将会有较快的发展。多功能、多工位级进模中发展重点是高精度、高效率和大型、高寿命的级进模。精冲模中发展重点是厚板精冲模大型精冲模，并不断提高其精度。

2、冲压模具技术发展重点。

模具技术未来发展趋势主要是朝信息化、高速化生产与高精度化发展。因此从设计技术来说，发展重点在于大力推广CAD/CAE/CAM技术的应用，并持续提高效率，特别是板材成型过程的计算机模拟分析技术。模具CAD、CAM技术应向宜人化、集成化、智能化和网络化方向发展，并提高模具CAD、CAM系统专用化程度。

为了提高CAD、CAE、CAM技术的应用水平，建立完整的模具资料库及开发专家系统和提高软件的实用性十分重要。从加工技术来说，发展重点在于高速加工和高精度加工。高速加工目前主要是发展高速铣削、高速研抛和高速电加工及快速制模技术。高精度加工目前主要是发展模具零件精度1μm以下和表面粗糙度Ra≦0.1μm的各种精密加工。提高模具标准化程度，搞好模具标准件生产供应也是冲压模具技术发展重点之一。

为了提高冲压模具的寿命，模具表面的各种强化超硬处理等技术也是发展重点。

对于模具数字化制造、系统集成、逆向工程、快速原型/模具制造及计算机辅助应用技术等方面形成全方位解决方案，提供模具开发与工程服务，全面提高企业水平和模具质量，这更是冲压模具技术发展的重点。

3、其他发展重点及展望。

其他发展重点及展望的内涵十分丰富，这里只就管理、专业化与标准化及行业调整三个方面作一些分析。

企业管理是一个系统工程，是一门学问，是科学技术。与工业发达国家模具企业相比，在某种意义上说，我们的管理落后更甚于技术落后。因此改进管理十分重要，且任务繁重，目前模具企业的管理有许多形式，各有其适应对象，但搞好信息化建设，逐步实现信息化管理已成为发展方向，行业也对此有共识。

由于历史和体制上的原因，我国模具专业化和标准化水平一直很低，其中冲压模具的专业化比塑料模和压铸模更低。这在一定程度上妨碍了冲压模具的发展，根据国内外模具专业化情况来看，专业化可以有多层意思：1）模具生产独立于其他产品生产，专业生产模具外供；2）按模具种类划分，专门从事某一类模具（如冲压模具）生产；3）在某一类模具中，按其服务对象或模具工艺及尺寸大小，选取该类模具中的某种模具（例如汽车覆盖件模具、多工位级进模具、精冲模具等等）进行专业化生产；4）专业生产模具中的某一些零件（如模架、冲头、弹性元件等）供给模具生产企业；5）按工序开展专业化协作。例如目前社会上专门从事模具设计的公司、专门进行型腔加工或电加工协作的企业、专门接受测量或热处理委托业务的企业及专业从事抛光业务的企业等等，这种多层次的专业化促进了模具行业的发展。但专业化的路途仍旧遥远，必须加快进程才能适应形势。因此，这也是发展重点。

行业调整是一个十分繁重的任务，模具行业更是如此。模具行业面临的调整任务主要有：

（1）模具企业组织结构的调整。使模具分厂（车间）独立出来，成为面向社会、自负盈亏的独立法人是调整的方向。模具企业按小而精、小而专、小而特的方向发展，并且在条件成熟情况下企业之间进行联合，以及发展产、学、研和科、工、贸相结合的联合体，也是调整的方向。规模效应也引起大家的重视。

（2）模具产品结构的调整。随着汽车工业、电子信息工业和家电工业的发展，冲压模具市场结构正在发生很大变化。与此相适应，冲压模具产品结构必须进行相应的调整。例如汽车覆盖件模具、汽车零件精冲模具、高精度高难度的引线框架冲模、接插件多工位级进模、各种电机定转子级进冲模等，其产品种类和产量必将有很大发展，有关企业必须根据市场需求来调整其产品结构。总体来看，应不断提高技术含量的大型、精密、复杂、长寿命模具的比例。

（3）模具技术结构的调整。21世纪已进入信息时代，信息时代的发展日新月异，模具行业和企业要发展必须把握时代脉搏，自觉主动地调整自已的技术结构。传统的模具设计制造技术必须用先进适用的高新技术进行改造，模具的技术含量必将逐步而快速地提高，现代化工业企业管理技术也必将逐步替代作坊式的管理模式。模具行业和模具企业，只有不断进行技术结构的调整，才能在瞬息万变的市场经济中立于不败之地。

（4）模具进出口结构的调整。2005年，我国冲压模具进口7.26亿美元，出口1.97亿美元，进出口相抵后净进口5.29亿美元，进出口之比3.7:1。我国的冲压模具出口量只占生产量的5%。这样的结构明显不合理。模具工业发达国家，模具产出中一般都有30%左右的出口，出口模具大大多于进口模具。我们虽然不可能在短时间内达到模具工业发达国家一样的进出口结构，但努力扩大出口，逐步改善结构，经过若干年努力，尽量做到进出口基本平衡，则应该是我们调整的目标。

在信息化带动工业化发展的今天，在经济全球化趋向日渐加速的情况下，我国冲压模具必须尽快提高水平。通过改革与发展，采取各种有效措施，在冲压模具行业全体职工的共同努力奋斗之下，我国冲压模具也一定会不断提高水平，逐渐缩小与世界先进水平的差距。“十一五”期间，在科学发展观指导下，不断提高自主开发能力、重视创新、坚持改革开放、走新型工业化道路，将速度效益型的增长模式逐步转变到质量和水平效益型轨道上来，我国的冲压模具的水平也必然会更上一层楼。

1.4、本次设计的意义

   这次毕业设计，是对我四年大学学习效果的有效检验方式。通过这次设计，能把课本上的知识和现实生产工作有机结合在一起，对即将走上社会工作的我们是一个很好的锻炼。在设计过程中，要查阅大量的资料，和老师、同学做良好的沟通，这也能培养我细心的习惯和团队合作精神，这对我以后的工作、生活是有很大帮助的。

第二章 冲压件工艺性分析及冲裁方案的确定

冲裁件的工艺性，是指冲裁件对冲裁工艺的适应性,即冲裁件的形状结构、尺寸大小、尺寸偏差、形位公差与尺寸基准等是否符合冲裁工艺的要求。冲裁件的工艺性对冲裁工件的质量、材料利用率、生产率、模具制造难易、模具寿命、操作方式及冲压设备的选用等都有很大的影响。一般情况下，对冲裁件工艺性影响最大是几何形状、尺寸、精度要求。良好的冲裁件工艺性能满足材料省、工序少、产品质量稳定、模具较易加工、操作方便且寿命较高等要求，从而显著降低冲裁件的制造成本。

参考文献

[1] 吴宗泽，罗圣国.机械设计课程设计手册.北京：高等教育出版社，1999 （2004重印）

[2] 姜奎华.冲压工艺与模具设计.北京：机械工业出版社，1998.5

[3] 王卫卫.材料成型设备.北京：机械工业出版社，2004.8

[4] 郝彬海.冲压模具简明设计手册.北京：化学工业出版社，2004.11

[5] 储凯，许斌，李先民，李维民.机械工程材料.重庆：重庆大学出版社2004.2

[6] 中国模具工业协会标准委员会编.中国模具标准件手册.上海：上海科学普及出版社，1989.

[7] 中国机械工程学会，中国模具设计大典委员会.中国模具设计大典.江西：江西科学技术出版社，2003.1

[8] 国家标准总局. 《冷冲压国家标准》.北京：《冷冲压国家标准》，1989

[9] 李天佑.《冲模图册》.北京：机械工业出版社，1998.

[10] 丁聚松.《冷冲模设计》.北京：机械工业出版社，1999.

[11] 赵孟栋主编.冷冲模设计（第2版）.北京：机械工业出版社，1997.

[12] 王孝培主编.冲压手册.北京：机械工业出版社，1990.

[13] 肖景容，姜奎华主编.冲压工艺学.北京：机械工业出版社，1990.


内容简介：
*Corresponding author. Tel.: #30-31-498-143; fax: #30-31-498-180.E-mail address: georgiadcperi.certh.gr (M.C. Georgiadis).Computers & Operations Research 29 (2002) 10411058An algorithm for the determination of optimal cutting patternsGordian Schilling?, Michael C. Georgiadis?*?Ciba Specialty Chemicals Inc., CH-1870 Monthey, Switzerland?Centre for Research and Technology - Hellas, Chemical Process Engineering Research Institute, P.O. Box 361,Thermi 57001, Thessaloniki, GreeceReceived 1 June 2000; received in revised form 1 September 2000; accepted 1 October 2000AbstractThis paper presents a new mathematical programming formulation for the problem of determining theoptimal manner in which several product rolls of given sizes are to be cut out of raw rolls of one or morestandard types. The objective is to perform this task so as to maximize the prot taking account of therevenuefrom the sales, the costs of the original rolls, the costs of changingthe cutting pattern and the costs ofdisposal of the trim. A mixed integer linear programming (MILP) model is proposed which is solved toglobal optimality using standard techniques. A number of example problems, including an industrial casestudy, are presented to illustrate the e$ciency and applicability of the proposed model.Scope and purposeOne-dimensional cutting stock (trim loss) problems arise when production items must be physicallydivided into pieces with a diversity of sizes in one dimension (e.g. when slitting master rolls of paper intonarrower width rolls). Such problems occur when there are no economies of scale associated with theproduction of the larger raw (master) rolls. In general, the objectives in solving such problems are to 5:? minimize trim loss;? avoid production over-runs and/or;? avoid unnecessary slitter setups.The above problem is particularly important in the paper converting industry when a set of paper rolls needto be cut from raw paper rolls. Since the width of a product is fully independent of the width of the raw papera highly combinatorial problem arises. In general, the cutting process always produces inevitable trim-losswhichhas to be burnedor processedin somewaste treatmentplant. Trim-lossproblems inthe paper industryhave, in recent years, mainly been solved using heuristic rules. The practical problem formulation has,therefore, in most cases been restricted by the fact that the solution methods ought to be able to handle theentire problem. Consequently, only a suboptimal solution to the original problem has been obtained and0305-0548/02/$-see front matter ? 2002 Elsevier Science Ltd. All rights reserved.PII: S 0 3 0 5 - 0 5 4 8 ( 0 0 ) 0 0 1 0 2 - 7very often this rather signicant economic problem has been left to a manual stage. This work presentsa novel algorithm for e$ciently determining optimal cutting patterns in the paper converting process.A mixed-integer linear programming model is proposed which is solved to global optimality using availablecomputer tools. A number of example problems including an industrial case study are presented to illustratethe applicability of the proposed algorithm. ? 2002 Elsevier Science Ltd. All rights reserved.Keywords: Integer programming; Optimization; Trim-loss problems; Paper converting industry1. IntroductionAnimportantproblemwhich is frequentlyencounteredin industriessuch as paperis related withthe most economic manner in which several product roll of given sizes are to be produced bycutting one or more wider raw rolls available in one or more standard widths. The solution of thisproblem involves several interacting decisions:? The number of product rolls of each size to be produced.This maybe allowedto varybetweengivenlower andupper bounds.The former normallyre#ectthe rm orders that are currently outstanding, while the latter correspond to the maximumcapacity of the market. However, certain discounts may have to be o!ered to sell sheets over andabove the quantities for which rm orders are available.? The number of raw rolls of each standard width to be cut.Rolls may be available in one or more standard widths, each of a di!erent unit price.? The cutting pattern for each raw roll.Cutting takes place on a machine employing a number of knives operating in parallel on a roll ofstandard width. While the position of the knives may be changed from one roll to the next, suchchanges may incur certain costs. Furthermore, there may be certain technological limitations onthe knife positions that may be realized by any given cutting machine.The optimal solution of the above problem is often associated with the minimization of thetrima waste that is generally unavoidable since rolls of standard widths are used. However,trim-loss minimization does not necessarily imply minimization of the cost of the raw materials(rolls) being used especially if several standard roll sizes are available. A more direct economiccriterion is the maximization of the prot of the operation taking account of:? the revenue from product rolls sales, including the e!ects of any bulk discounts;? the cost of the rolls that are actually used;? the costs, if any, of changing the knife positions on the cutting machine;? the cost of disposing of trim waste.The above constitutes a highly combinatorial problem and it is not surprising that traditionallyits solution has often been carried out manually based on human expertise. The simplied versionof this problem is similar to the cutting stock problem known in the operation-research literature,where a number of ordered pieces need to be cut o! bigger stored pieces in the most economicfashion. In the 1960s and the 1970s, several scientic articles were published on the problem of1042G. Schilling, M.C. Georgiadis / Computers & Operations Research 29 (2002) 10411058minimizing trim loss, e.g. 1,2. Hinxman 3 presents a good overview of the available solutionmethods for trim-loss and assortment problems.Gilmore and Gomory 1 presented a basic linear programming approach to the cutting stockproblem while relaxing some integer-characters of the problem. Gilmore and Gomory 2 de-scribed an iterative solution method that is suitable for very large number of orders and iscomputational cheap, but the resulting values for the number of cutting patterns to be used arenon-integer and it is not possible to prove the optimality or indicate the margin of optimality ofthese cutting patterns. Thus, the rounding values obtained by the algorithm of Gilmore andGomory 2 may very probably result in poor economic performance. Wascher 4 presenteda linear programming approach to cutting stock problems taking into account multiple objectivessuch as cost of the raw materials, cost of the overproduction storage, trim-loss removal costs, etc.Sweeny 5 proposed a heuristic procedure for solving one-dimensional cutting stock problemswith multiple quality grades. Ferreira et al. 6 considered the two-phase roll cutting problemsbased on a heuristic approach. Gradisar et al. 7 presented an e$cient sequential heuristicprocedure and a software tool for optimization of roll cutting in the clothing industry. Later,Gradisaret al. 8 developedan improvedsolution strategy based on a combination of approxima-tions and heuristics leading to almost optimal solutions for the one-dimensional stock cuttingproblems. A software tool was also developed.In recent years, integer programming techniques have been used for the solution of the trim-lossand production optimization problem in the paper industry. The work of Westerlund andcoworkers at A ? bo Akademi University in Finland is a key contribution in this area. Harjunkoski9 considered a mathematicalprogrammingapproachto the trim-lossproblemand presentedtwodi!erent types of formulation. In the rst one, both the cutting patterns that need to be used andthe number of rolls that have to be cut according to each such pattern are treated as unknowns.This results in an integer nonlinear mathematical problem (INLP) involving bilinear problems ofthe variables characterizing each cutting pattern and the corresponding number of rolls cut in thisway. Two di!erent ways of linearizing the INLP to obtain a mixed integer linear programming(MILP) mode were presented. However, these linearizations often result in a signicant increase inthe number of variables and constraints, as well as a large integrality gap. The second type offormulation presented by Harjunkoski 9 is based on using a xed set of cutting patterns that isdecided a priori. This results in a MILP that has a much smaller integrality gap than the oneresulting from the linearization of the INLP formulation mentioned above. However, the solutionobtained is guaranteed to be optimal only if all non-inferior cutting patterns are identied andtaken into consideration. The number of such patterns may be quite substantial for realisticindustrial problems. Extending the above work, Harjunkoski 10 presented linear and convexformulations for solving the non-convex trim-loss problems.Westerlund 11 considered the two-dimensional trim-loss problem in paper converting. A non-convex optimization model was proposed where both the widths and the lengths of the raw paperwere considered as variables. A two-step solution procedure was used where all feasible cuttingpatterns were rst generated and then a MILP problem was solved. In a similar fashion, theproduction optimization problem in the paper converting industry was addressed by Westerlund12. Scheduling aspects of the cutting machines in paper converting were simultaneously con-sidered with the trim-loss problem by Westerlund 13. Recently, Harjunkoski 14 incorporatedenvironmental impact considerations into a general framework for trim-loss minimization.G. Schilling, M.C. Georgiadis / Computers & Operations Research 29 (2002) 104110581043This paper presents an alternative mathematical programming formulation that results directlyin a MILP of small integrality gap. The salient feature of this model is that it does not requirea priori enumeration of all possible cutting patterns. The next section presents a formal statementof the problem under consideration and the notation used. Section 3 considers the mathematicalformulation of the objective function and the operational constraints. This is followed by someexample problems including an industrial case study illustrating the applicability and computa-tional behavior of the proposed formulation.2. Problem statement and dataThe task being considered here is to produce product rolls of I di!erent types, the width of typei being denoted by B?, i1,2,I from one or more standard rolls. The lengths of all raw rolls andof the product rolls resulting from them are assumed to be identical and xed. It is beyond thescope of this work to consider the two-dimensional problem where both the widths and the lengthsof raw paper rolls and the cutting patterns are considered variables.Product rolls are mostly produced to order. The minimum ordered quantity for product rolls ofwidth i is denoted by N?and is given, and so is the corresponding unit price p?. However,customers may be willing to buy additional rolls of type i up to a maximum quantity N?subjectto a discount of c?for each product roll over and above the minimum number N?. In general,the number of additional rolls sold in this manner tends to be rather small since the main incentiveof such discounting from the point of view of the manufacturer is merely to decrease the lossthrough trim.The product rolls are to be cut from raw rolls of di!erent standard types. The unit price fora raw roll of type t is denoted by c?and its nominal width by B?. However, the useful width ofa roll of type t is determined by the cutting machine used. In particular, each raw roll typet1,2, is characterized by a maximum possible total engagement B?denoting the maximumtotal width of all product rolls that can be cut from a raw roll of this type. There may also bea minimum required total engagement B?for this type of roll. In generalB?)B?)B?,t1,2,.The maximum number N?of product rolls that can be cut out of a raw roll of type t willgenerally be determined by the knives and other characteristics of the available machine.Moreover,in some cases, there maybe limitationsin the available number JH?of raw rolls of a giventype t.The cutting pattern for each raw roll is determined by the position of the knives. Frequentchanges in these positions are generally undesirable. Each such change may therefore be associatedwith a non-zero cost c?.The production of the required product rolls from the available raw rolls may result in trimwaste which may need to be disposed of. The cost of such disposal per unit width of trim is denotedby c?.Based on the given data, we rst derive an upper bound J on the number of raw rolls that mayneed to be cut. This is obtained by assuming that the maximum number N?of product rolls ofeach type i will be produced; that raw rolls of the type t that permits the smallest minimum1044G. Schilling, M.C. Georgiadis / Computers & Operations Research 29 (2002) 10411058engagement B?will be used; and that each raw roll will be used to produce product rolls ofa single type only. Overall, this leads to the following upper bound on the number of raw rolls thatmay be required:J?N? min?B?/B?.(1)We can also calculate a lower bound J? on the minimum number of raw rolls that arenecessary to satisfy the minimum demand for the existing orders. We do this by assuming that rollsof the type t allowing the maximum possible engagement B?are used, and that no trim isproduced. However, we must also take account of possible limitations on the number of availableknives. Overall, this leads to the following lower bound on the number of rolls that maybe required:J?max?N?B?max?B?,?N?max?N?.(2)3. Mathematical formulationThe aim of the mathematical formulation is to determine the type t of each raw roll j to be cutand the number of product rolls of each type i to be produced from it.3.1. Key variablesThe following integer variables are introduced:n?: number of product rolls of type i to be cut out of raw roll j?: number of product rolls of type i produced over and above the minimum number ordered.We note that n?cannot exceed:? the maximum number N?of product rolls of type i that can be sold;? the maximum number of product rolls of width B?that can be accommodated within a max-imum engagement B?for a raw roll of type t;? the maximum number N?of knives that can be applied to a raw roll of type t.This leads to the following bounds for n?:0)n?)min?N?, max?B?B?, max?N?i1,2,I, j1,2,J?.(3)Also0)?)N?!N?,i1,2,I.(4)G. Schilling, M.C. Georgiadis / Computers & Operations Research 29 (2002) 104110581045We note that ?need to be included in the model only if N?N?. We also introduce thefollowing binary variables:y?1if the jth roll to be cut is of type t,0otherwise.z?1if the cutting pattern for paper roll j is different to that for roll j!1,0otherwise.We note that, in general, the index j will be in the range 1,2,J?. However, the formulationto be presented will assign a type t only to the raw rolls j that are actually used. Hence, the totalnumber of rolls to be cut will also be determined by the solution of the optimization problem. Thiswill become clearer in the next subsection.3.2. Roll type determination constraintsEach raw roll j to be cut must be of a unique type t. This results in the following constraints:?y?1,j1,2,J?,(5a)?y?)1,jJ?#1,2,J?.(5b)Note that for jJ?, it is possible that y?0 for all types t; this simply implies that it is notnecessary to cut roll j.Furthermore, the limited availability of raw rolls of a given type t may be expressed in terms ofthe constraint?y?)JH?,t1,2,.(6)3.3. Cutting constraintsWeneed to ensure that, if a roll j is to be cut, then the limitations on the minimumand maximumengagement are observed. This is achieved via the constraints?B?y?)?B?n?)?B?y?,j1,2,J?.(7)We note that the quantity ?B?n?represents the total width of all product rolls to be cut out ofraw roll j. If y?1 for some roll type t, then constraint (7) ensures thatB?)?B?n?)B?.1046G. Schilling, M.C. Georgiadis / Computers & Operations Research 29 (2002) 10411058On the other hand, if y?0 for all t, then constraint (7) e!ectively forces n?0 for all i1,2,I.This expresses the obvious fact that if roll j is not actually cut, then no product rolls of any type canbe produced from it.We also need to ensure that the number of product rolls cut out of any roll j of type t does notexceed the number of knives that can be deployed on rolls of this type. This is written as0)?n?)?N?y?,j1,2,J?.(8)3.4. Production constraintsThe total number of product rolls of each type i that are produced comprises the minimumordered quantity N?for this type plus the surplus production ?:?n?N?#?,i1,2,I.(9)These constraints, together with the bounds on ?, ensure that the quantity of product rolls of typei produced lies between the minimum and maximum bounds N?and N?, respectively.3.5. Changeover constraintsIf changing the cutting pattern incurs a non-zero cost c?0, we need to determine whensuch changes will take place. To this end, we include the following constraint:!M?z?)n?!n?)M?z?,i1,2,I, j2,2,J?.(10)Note that this will allow z?to be zero only if n?n?for all product rolls i, i.e. if rolls j and j!1are cut in exactly the same way. Here, the constant M?is an upper bound on n?(see Section 3.1).3.6. Objective functionThe objective of the optimization is to maximize the total prot of the operation taking accountof:? The income from the sales of product rolls of each type i.This comprises the income from selling the minimum ordered quantities N?at the full unitprice p?, plus the income of selling the additional quantities ?at the discounted unit pricep?!c?:?(p?N?#?(p?!c?).? The costs of the rolls to be cut.Generally, the cost of each roll depends on its type. The total cost can be written as?c?y?.G. Schilling, M.C. Georgiadis / Computers & Operations Research 29 (2002) 104110581047We note that, for each roll j, at most one term of the inner summation is non-zero (cf. constraints(5a) and (5b).? The costs of changing the positions of the knives.In general, the knife positions have to be changed if the cutting pattern used for a given roll j isdi!erent to that for the previous one. This is determinedby the variablesz?and results in the costtermc?z?,where the summation is equal to the total number of changes that are necessary.? The cost of disposing of any trim produced.The width of trim produced out of raw roll j is given by the di!erence between the roll width andthe total width of all product rolls cut from it. The former quantity depends on the type of theroll and can be expressed as ?B?y?; once again, at most one of the terms in this summationcan be non-zero (cf. constraints (5a) and (5b). The latter quantity is given by ?B?n?. Overall,trim disposal results in the following cost termc?B?y?!?B?n?.The above terms can now be collected in the following objective function:max?(p?N?#?(p?!c?)!?c?y?!c?z?!c?B?y?!?B?n?.(11)Note that the rst term in the above objective function (i.e. ?p?N?) is actually a constant anddoes not a!ect the optimal solution obtained.3.7. Degeneracy reduction and constraint tighteningIn general, the basic formulation presented above is highly degenerate: given any feasible point,one can generate many others simply by forming all possible ordering of the rolls selected to be cut.Moreover,provided all raw rolls of the same type are cut consecutively, all these feasible points willcorrespond to exactly the same value of the objective function.Theabove propertymay haveadversee!ects on the e$ciencyof the searchprocedure.Therefore,in order to reduce the solution degeneracy without any loss of optimality, we introduce thefollowing ordering constraints:?n?*?n?,j2,2,J?.(12)This ensures that the total number of product rolls cut out of raw roll j!1 is never lower than thecorresponding number for roll j; all completely unused raw rolls are left last in this ordering.1048G. Schilling, M.C. Georgiadis / Computers & Operations Research 29 (2002) 10411058An alternative would be to order the raw rolls in non-increasing utilization order, i.e.?B?n?*?B?n?,j2,2,J?.However, our practical experience indicates that this is not as e!ective as constraint (12).We also note that the constraints (7) implicitly impose a lower bound on the total number ofproduct rolls ?n?cut out of a raw roll j. A stronger bound may sometimes be obtained byconsidering a roll of type t being used at the minimum possible engagement to produce the widestpossible product rolls. This leads to the constraints?B?max?B?y?)?n?,j1,2,J?.(13)3.8. CommentsThe objectivefunction and all constraints introducedin this section are linear. Since all variablesare integer valued, the formulation presented corresponds to an integer linear programming (ILP)problem. However, constraints (9) ensure that the variables ?will automatically assume integervalues provided variables n?do so. Therefore, ?may be treated as continuous quantities, whichleaves us with a mixed integer linear programming (MILP) problem. In principle, the latter can besolved using standard MILP solvers.In the special (but quite common) case where only one type of roll is available, constraints (5a)simply imply that y?can be xed to 1 for all j1,2,J?. Both (5a) and (5b) are otherwiseredundant and may be dropped. Furthermore, the lower bound on constraint (7) is directlyincluded in the bounds of the corresponding slack variable, 0; B?!B?, which results in oneless constraint for each roll j.4. Example problemsIn this section, we consider four example problems of increasing complexity in order toinvestigatethe computationalbehaviorof our formulation.Furthermorean industrial case study isalso presented. In all cases, we assume that the maximum raw roll engagement B?is equal to thecorrespondingroll widthB?.The GAMS/CPLEXvs 6.0 solverhas beenused for the solution15and all computations were carried out on a AlphaServer 4100. An integrality gap of 0.1% wasassumed for the solution of all problems.4.1. Example 1Our rst example is based on that given by Harjunkoski 9. Some translation of the variouscost coe$cients was necessary to account for slight di!erences in the objective functions used bythe two formulations.Also note that the objective used by those authors is the minimizationof costas opposed to the maximization of prot; therefore, the sign of their objective function is oppositeto that of ours.G. Schilling, M.C. Georgiadis / Computers & Operations Research 29 (2002) 104110581049Table 1Raw roll characteristics for Example 1Roll typeWidth B?Max. spill B?!B?Max. cuts N?Cost c?11900 mm200 mm51900Table 2Production data for Example 1Product rolltype iWidth B?(mm)Min. quantityN?Max. quantityN?Pricep?Discountc?1330810297.00236078324.0033851213346.5044151111373.50?Each vertical bar corresponds to a di!erent roll being cut. The corresponding roll type is shown immediately aboveeach bar. Each bar is divided into a number of segments corresponding to sheets of the indicated type. The dark shadedsegment at the top of the bar is the trim-loss, the percentage width of which is indicated numerically at the bottom of thegure.The problem aims to determine the optimal cutting pattern for producing four di!erent types ofproduct rolls from a single type of raw roll. The characteristics of the latter are shown in Table 1.The production requirements are summarized in Table 2. The cost for changing the cutting patternis 1, while disposing of the trim incurs no cost.Harjunkoski 9 assumed a maximum of four di!erent cutting patterns, which results ina reduction of the size of the model. In our case, the number of such patterns is determined by thesolution. Also from expressions (1) and (2), we determine J?10 and J?8. We therefore xy?1, for j1,2, 8.The solution we obtain is the same as that reported by Harjunkoski 9 involving the productionof the minimum ordered amounts of product rolls plus one extra roll of type 2 and another of type 3.The solution is presented pictorially in Fig. 1? and corresponds to an objective function value of!1622.0; thus, with the given economic data the operation incurs a loss.The optimal solution (within a margin of optimality of 0.1%) is found within less than 1 CPU sat node 49 of the branch-and-bound algorithm using a breadth rst search strategy. It must benoted that the integrality gap of our formulation is comparable to that for one of the formulationspresented by Harjunkoski 9 despite the fact that it does not employ any a priori enumeration ofthe cutting patterns. Our formulation also examines a small number of nodes in order to detect theoptimal point (Table 3).1050G. Schilling, M.C. Georgiadis / Computers & Operations Research 29 (2002) 10411058Fig. 1. Solution of Example 1.Table 3Computational statistics for Example 1OptimalobjectiveFully relaxedobjectiveIntegralitygap (%)Nodesin B&BVariables(Bin/Int/Cont)Constraints(!)1622.0(!)1619.40.184960(13/44/3)1154.2. Example 2The data for this problem are given in Tables 4 and 5. There is no cost for changing the cuttingpattern or for disposing of trim. Using expressions (1) and (2), it is possible to calculate a priori thatthe number of raw rolls required will be between 11 and 15.Although this problem involves only 9 types of product rolls, there are a total of 3971 di!erentcutting patterns, all of which are feasible with respect to the minimum and maximum allowed totalengagement of the rolls, the maximum number of knives that can be applied to a roll and themaximum quantities of sheets ordered. Thus, any formulation that relies on explicit patternenumeration would have to involve a large number of discrete variables. This is, of course,a well-known problem with the classical approach to the cutting stock problem.Our algorithm obtains the exact (0% optimality margin) optimal solution for this problemwithin less than 1 CPU s. This solution is presented in Fig. 2. Computational performancestatistics are given in Table 6.G. Schilling, M.C. Georgiadis / Computers & Operations Research 29 (2002) 104110581051Table 4Raw roll characteristics for Example 2Roll typeWidth B?Max. spill B?!B?Max. cuts N?Cost c?11900 mm200 mm51600Table 5Production data for Examples 2 and 3Product rolltype iWidth B?(mm)Min. quantityN?Max. quantityN?Pricep?Discountc?1340810C 340C 0236578C 365C 033851213C 385C 04415111C 415C 0543555C 435C 0626068C 260C 0730044C 300C 0832078C 320C 0933533C 335C 0Fig. 2. Solution of Example 2.1052G. Schilling, M.C. Georgiadis / Computers & Operations Research 29 (2002) 10411058Table 6Computational statistics for Examples 2, 3 and 4FormulationOptimalFully relaxedIntegralityNodesVariablesConstraintsobjectiveobjectivegap (%)in B&B(Int/Bin/Cont)Example 22590.02630.01.5443173(6/162/5)61Example 33030.03030.00131203(36/162/5)116Example 41240.01279.33.1614,800173(6/162/5)61Table 7Raw roll characteristics for Example 3Roll typeWidth B?Max. spill B?!B?Max. cuts N?Cost c?11900 mm200 mm5C 160022200 mm250 mm6C 18504.3. Example 3Thisexample is similar to Example2, the only di!erencebeing that up to 6 raw rolls of a di!erenttype are now also available to be cut (see Table 7). Since a wider roll is now available, the minimumnumber J? of required rolls is reduced to 9 (from 11 in Example 2), but the maximum numberJ? of rolls remains the same, namely 15.The exact (0% optimality margin) optimal solution was obtained in less than 1 CPU s. Thesolution is presented in Fig. 3 with the computationalperformance statistics shown in Table 6. Themaximum possible number of raw rolls of type 2 is used. It is interesting to mention that, if noupper limit on the number of raw rolls of type 2 is imposed, only rolls of this type are actuallyengaged. This then results in a higher prot of C 3380.4.4. Example 4This example is similar to Example 2, the only di!erence being that the cost coe$cients forchanging the cutting pattern, c? and for disposing of waste trim, c? are equal to 10 and 1,respectively. The computational performance is shown in Table 6. We observe that a considerablelarger number of nodes in the branch-and-bound tree is required comparing with Example 2.However, the integrality gap is relatively small.4.5. Example 5One justied concern with our formulation is the way in which the computational cost mayincrease with the number of orders that have to be satised. This is because more orders willG. Schilling, M.C. Georgiadis / Computers & Operations Research 29 (2002) 104110581053Fig. 3. Solution of Example 3.Table 8Computational statistics for Example 5Example 2OptimalFullyrelaxedNodes inB&BCPU(s)Variablesint/contConstraintsNumber of rollsordersobjectiveobjectiveMin.Max.UsedOriginal2590263043(1178/564111513Twice52605260206(1336/51152130274-times10,52010,5208283623/520843595410-times26,30026,3005610201500/549310614613420-times52,60052,6006250313519/5893248293268generallyimply moreraw rolls having to be consideredfor cutting,(i.e., higher J?). The numberofvariables and constraints in our formulation increases linearly with the latter.In order to study how the computational performance of the presented formulation varies withthe number of ordered product rolls, we carried out three additional experiments using the originaldata of Example 2 but multiplying the ordered quantities (cf. Table 8) by factors of 2, 4, 10 and 15,respectively.The results are summarized in Table 8. As expected the bigger the number of ordered productrolls, the larger the resulting mathematical problem and the di$culty of its solution. For instance,the optimal solution of the problem with twice the number of orders makes use of 25 di!erentcutting patterns which are automatically determined by the algorithm. However, even with the1054G. Schilling, M.C. Georgiadis / Computers & Operations Research 29 (2002) 10411058Table 10Production data for the industrial case studyProduct rolltype iWidth B?(cm)Min. quantityN?Max. quantityN?Pricep?Discountc?11331010C 309C 029155C 211C 0385.533C 177C 0410111C 209C 058466C 240C 065044C 143C 073955C 93C 085433C 128C 0Table 9Raw roll characteristics for industrial case studyRoll typeWidth B?Max. spill B?!B?Max. cuts N?Cost c?1360 cm40 cm9C 515largest problem (involving the production of 1340 product sheets from 268 raw rolls), it is stillpossible to determine the optimal solution in less than 1 min of computation on a desktopworkstation. The integrality gap also remains very small in all examples. The same problem wasalso solved for the case where there are two di!erent types of rolls available (as in Example 3)and the total number of orders exceeds 600 sheets. The solution corresponds to an objectivefunction of C 31550 with zero integrality gap. The total number of sheets produced is 660from 120 raw rolls. The problem involves 1823 integer variables and the solution was obtainedin 43 CPU s.4.6. Industrial case studyThis is an industrial case study based on a daily trim-loss optimization problem at MacedonianPaper Mills (MEL) S.A. in Northern Greece. MEL is one of the major paper-producing companiesin Greece with an annual production of more than 100,000 tons. A daily order typically includes515 di!erent types of product rolls with a total weight of 10100 tons. So far, minimizationof trim-loss has been performed using heuristic-based techniques and human expertise withan average trim-loss of 47% depending on the order. The data for this problem are given inTables 9 and 10 and correspond to approximated values.Assuming no cost for disposing of waste trim and for changing the cutting pattern the solutionis depicted Fig. 4. Note that 9 raw rolls are required to satisfy the production. A total number of1100 nodes were examined in the branch-and-bound tree requiring a computational time of lessG. Schilling, M.C. Georgiadis / Computers & Operations Research 29 (2002) 104110581055Fig. 4. Solution of industrial case study without waste disposal and cutting change cost.Fig. 5. Solution of industrial case study with waste disposal and cutting change cost.than 5 CPU s. The optimal value of the objective function which represent the prot is C3105.8and it is equal to the fully relaxed objective. The average trim-loss is 1.126% and representsapproximately a 55% improvement comparing with the current practice based on purely humanexpertise.The same problem was also solved by assuming that the cost coe$cients for disposing of wasteand for changing the cutting patterns are equal to 0.39 and 58.8, respectively (see Fig. 5). Theoptimal value of the prot is now C2842 while the value of the fully relaxed problem is C3044.Approximately 9000 nodes were considered requiring a computational time of 1 CPU min. It is1056G. Schilling, M.C. Georgiadis / Computers & Operations Research 29 (2002) 10411058interesting to note that, since the cost for changing the cutting pattern is taken into account, onlythree such changes take place while the average trim-loss remains the same with the previous case.However, it should be emphasized that the time savings in cutting, due to simultaneous minimiz-ation of changing the cutting pattern, has signicant impact on the protability of the plant. This isbecause the production rate increases almost proportionally with the reduction of total cuttingtime.5. ConclusionsThis paper has presented a new mathematical formulation for the determination of optimalcutting patterns in one-dimensional problems. Its main advantage over earlier formulations lies inits small integralitygap and its fewer variablesand constraints. This is achievedwithoutthe needtoresort to a priori generated cutting patterns, and the combinatorial increase in problem size arisingfrom such an approach.The formulation results in MILP problems of modest size that are within the scope of currentlyavailable commercial solvers. The integrality gap of the formulation is generally small, althoughthe di$culty of solution increases with problems involving changeover and waste disposal costs.Both the formulation presented here and most of the earlier ones reviewed in this paper areprimarily concerned with ensuring that the various orders are fullled. Only the work of Wester-lund 13 actually considers the times at which such orders are due. One interesting aspect of thepresented formulation is that it explicitly characterizes the sequence of rolls that have to be cut interms of both the type of each raw roll and the cutting pattern used for it. This opens the possibilityfor introducing additional variables and constraints
温馨提示:
1: 本站所有资源如无特殊说明，都需要本地电脑安装OFFICE2007和PDF阅读器。图纸软件为CAD,CAXA,PROE,UG,SolidWorks等.压缩文件请下载最新的WinRAR软件解压。
2: 本站的文档不包含任何第三方提供的附件图纸等，如果需要附件，请联系上传者。文件的所有权益归上传用户所有。
3.本站RAR压缩包中若带图纸，网页内容里面会有图纸预览，若没有图纸预览就没有图纸。
4. 未经权益所有人同意不得将文件中的内容挪作商业或盈利用途。
5. 人人文库网仅提供信息存储空间，仅对用户上传内容的表现方式做保护处理，对用户上传分享的文档内容本身不做任何修改或编辑，并不能对任何下载内容负责。
6. 下载文件中如有侵权或不适当内容，请与我们联系，我们立即纠正。
7. 本站不保证下载资源的准确性、安全性和完整性, 同时也不承担用户因使用这些下载资源对自己和他人造成任何形式的伤害或损失。
提示  人人文库网所有资源均是用户自行上传分享，仅供网友学习交流，未经上传用户书面授权，请勿作他用。
关于本文
本文标题：接线端子板的冲孔、落料、压弯复合模设计【优秀】【word+10张CAD图纸全套】【冲压复合模类】【毕设】
链接地址：https://www.renrendoc.com/p-298491.html

官方联系方式

网站客服网站客服      侵权投诉侵权投诉
1:下载资料失败解决办法   
2:不支持迅雷下载,请使用浏览器下载   
3:不支持QQ浏览器下载,请用其他浏览器   
4:下载后的文档和图纸-无水印   
5:文档经过压缩，下载后原文更清晰   
点击下载此资源
关于我们 - 网站声明 - 网站地图 - 资源地图 - 友情链接 - 网站客服 - 联系我们

网站客服QQ：2881952447     

copyright@ 2020-2025  renrendoc.com 人人文库版权所有   联系电话：400-852-1180

备案号:蜀ICP备2022000484号-2       经营许可证: 川B2-20220663       公网安备川公网安备: 51019002004831号

本站为文档C2C交易模式，即用户上传的文档直接被用户下载，本站只是中间服务平台，本站所有文档下载所得的收益归上传人(含作者)所有。人人文库网仅提供信息存储空间，仅对用户上传内容的表现方式做保护处理，对上载内容本身不做任何修改或编辑。若文档所含内容侵犯了您的版权或隐私，请立即通知人人文库网，我们立即给予删除！