首页 人人文库网 > 图纸下载 > 毕业设计 > 空气滤清器连接板的冲孔、冲槽、落料复合模设计【优秀】【word+12张CAD图纸全套】【冲压复合模类】【毕设】
译文.doc

空气滤清器连接板的冲孔、冲槽、落料复合模设计【优秀】【word+12张CAD图纸全套】【冲压复合模类】【毕设】

收藏

压缩包内文档预览：
预览图 预览图 预览图 预览图 预览图 预览图 预览图 预览图 预览图 预览图 预览图 预览图 预览图 预览图 预览图 预览图
编号：298663    类型：共享资源    大小：968.31KB    格式：RAR    上传时间：2014-07-24 上传人：QQ14****9609 IP属地：陕西
45
积分
举报
举报 版权申诉
版权申诉 word格式文档无特别注明外均可编辑修改；预览文档经过压缩，下载后原文更清晰！ 立即下载
关 键 词：
空气滤清器 连接板 冲孔 复合 设计 优秀 冲压
资源描述：

空气滤清器连接板的冲孔、冲槽、落料复合模的设计【优秀】【word+12张CAD图纸全套】【冲压复合模类】【毕业设计】

【带任务书+开题报告+评阅评语表+答辩资格审查表+工作中期检查表+指导教师评阅表+外文翻译】【40页@正文13900字】【详情如下】【需要咨询购买全套设计请加QQ1459919609】

任务书.doc

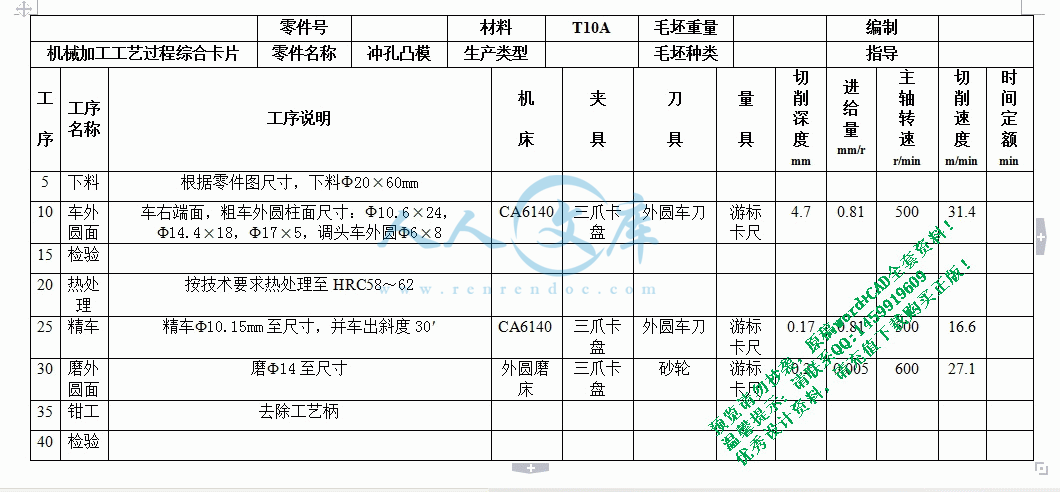
冲孔凸模机械加工工艺过程综合卡片.doc

合计12张零件图及总装图.dwg

外文原文.pdf

工作中期检查表.doc

开题报告+任务书.doc

开题报告.doc

指导教师审阅表.doc

正文.doc

答辩及最终成绩评定表.doc

答辩资格审查表.doc

表格.doc

评阅教师评阅表.doc

译文.doc

任务书

课题名称空气滤清器连接板冲孔、冲槽、落料复合模设计

内容及任务

设计图纸

模具总装图一张

全部模具零件图纸（其中至少有一张电脑绘图）

所有图纸折合成0号图不得少于3张。

设计说明书

1、资料数据充分，并标明数据出处。

2、计算过程详细、完全。

3、公式的字母含义应标明，有时还应标注公式的出处。

4、内容条理清楚，按步骤书写。

5、说明书要求用计算机打印。

6、设计说明书按要求格式独立撰写，不少于12000字。

自选一个重要模具零件编制加工工艺路线，进行相关的计算，并编制加工工艺卡和工序卡。

翻译一篇本专业外文文献（10000个以上印刷符号），并附译文。

拟达到的要求或技术指标1、保证规定的生产率和高质量的冲压件的同时，力求成本低、模具寿命长。

2、设计的冷冲模必须保证操作安全、方便。

3、冲模零件必须具有良好的工艺性，即制造装配容易、便于管理。

4、便于搬运、安装、紧固到冲床上并且方便、可靠。

5、保证模具强度前提下，注意外形美观，各部分比例协调。

进度安排起止日期工作内容备注

2周

（2.28~3.11）毕业调研

2周

（3.14~3.25）集中实习

10周

（3.28~6.3）毕业设计

1周

（6.6~6.10）毕业答辩

主要参考资料１、《冷冲压工艺及模具设计》刘心治主编重庆大学出版社

２、《冲压工艺及模具设计》万战胜主编 铁道出版社

３、《冲模设计》 吉林人民出版社

４、《实用冲压技术》 机工出版社

５、《冷冲压及塑料成型工艺与模具设计资料》 机工出版社

６、《模具设计与制造简明手册》 冯炳尧等编 上海出版社

7、《冲压工艺模具设计实用技术》　郑家贤编　机械工业出版社

8、《实用板金冲压工艺图集》　梁炳文主编　机械工业出版社

9、《几何量公差与检测》甘永立主编　上海科学技术出版社

10、《机械制造专业英语》章跃主编　机械工业出版社

摘  要



本设计为一垫板的冷冲压模具设计，根据设计零件的尺寸、材料、批量生产等要求，首先分析零件的工艺性，确定冲裁工艺方案及模具结构方案，然后通过工艺设计计算，确定排样和裁板，计算冲压力和压力中心，初选压力机，计算凸、凹模刃口尺寸和公差，最后设计选用零、部件，对压力机进行校核，绘制模具总装草图，以及对模具主要零件的加工工艺规程进行编制。其中在结构设计中，主要对凸模、凹模、凸凹模、定位零件、卸料与出件装置、模架、冲压设备、紧固件等进行了设计，对于部分零部件选用的是标准件，就没深入设计，并且在结构设计的同时，对部分零部件进行了加工工艺分析，最终才完成这篇毕业设计。


关键词：模具；冲裁件；凸模；凹模；凸凹模




ABSTRACT



  The design for a plate of cold stamping die design, according to the size of the design components, materials, mass production, etc., the first part of the process of analysis to determine the blanking process planning and die structure of the program, and then through the process design calculations, determine the nesting and cutting board, calculate the pressure and pressure washed centers, primary presses, computing convex and concave Die Cutting Edge dimensions and tolerances, the final design selection of parts and components, to press for checking, drawing die assembly drawings, as well as Mold processing technology of the main parts to the preparation procedures. In which the structural design, primarily to the punch and die, punch and die, positioning parts, unloading and out of pieces of equipment, mold, pressing equipment, fasteners, etc. has been designed, for the selection of some components are standard parts , there is no in-depth design, and structural design, while some parts for the processing process analysis and ultimately to complete this graduation project.

Key words  mold; stamping parts; punch; die; punch and die


目  录


1  前言1

1.1未来冲压模具制造技术发展趋势1

1.2 模具技术发展的几个特点2

1.2.1 以计算机为中心2

1.2.2 模具设计水平高2

1.2.3 生产设备先进2

1.3 我国锻压工业的现状及发展对策3

2  零件工艺性分析4

2.1 冲裁工艺性4

2.1.1 结构与尺寸4

2.1.2 精度4

2.1.3 材料5

3  确定冲裁工艺方案6

3.1 工序性质与数量的确定6

3.2 工序顺序的确定6

3.3 工序组合方式的确定6

4  确定模具总体结构方案7

4.1 模具类型7

4.2 操作与定位方式7

4.3 卸料方式与出件方式7

4.4 模架类型及精度7

5  工艺与设计计算8

5.1 排样设计与计算8

5.2 计算冲压力与压力中心，初选压力机9

5.2.1 计算工艺力9

5.3 计算凸、凹模刃口尺寸及公差11

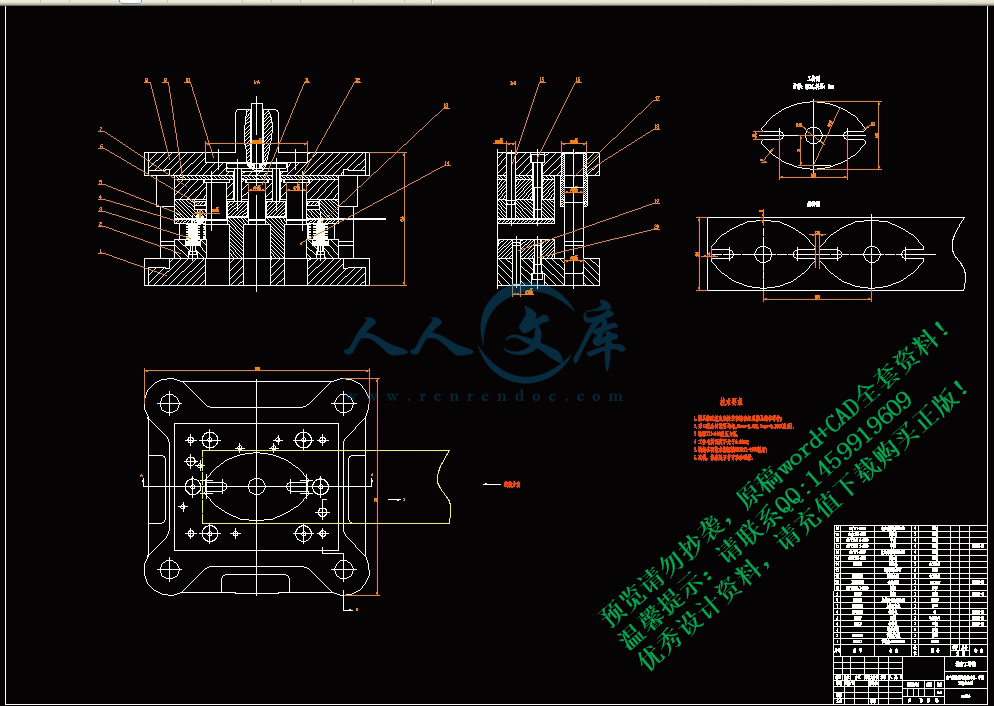
6  设计选用模具零部件、绘制模具总装草图14

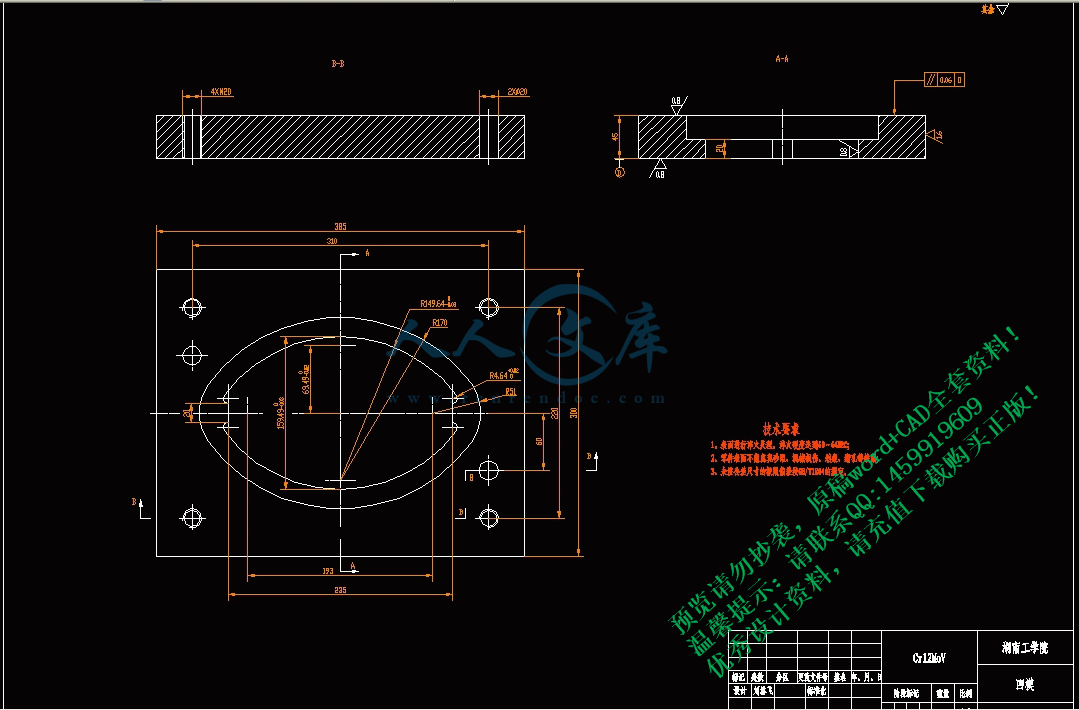
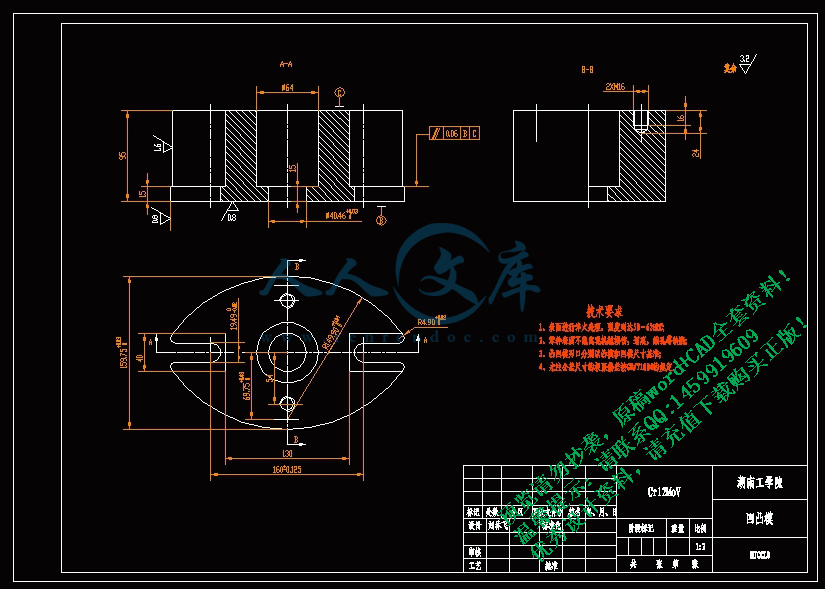
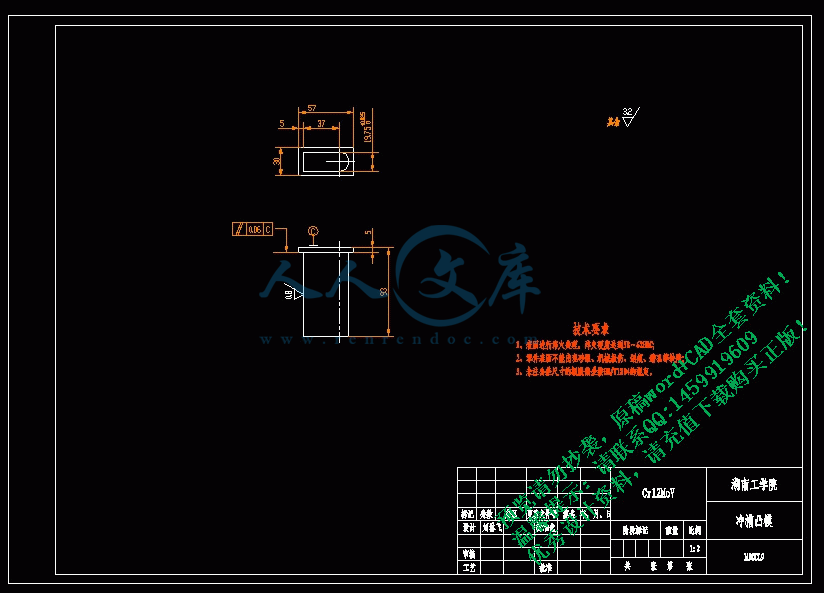
6.1  确定凸、凹模结构形式，计算凹模轮廓尺寸及凸模结构尺寸14

6.1.1 凹模设计14

6.1.2 凸模设计14

6.2 设计选用定位零件15

6.3 卸料与出件装置15

6.3.1 固定卸料装置16

6.4 模架及零件17

6.4.1 模架17

6.4.2 其它支承与固定零件19

6.4.3 紧固件：螺钉与销钉的选用21

7  确定冲压设备25

8  模具的装配26

8.1 复合模的装配26

8.2 凸、凹模间隙的调整26

9  重要零件的加工工艺过程编制28

10 结  论31

致  谢32

参考文献33

1  前言

随着国民经济的高速发展，市场对模具的需求量不断增长。近年来，模具工业一直以15%左右的增长速度快速发展，模具工业企业的所有制成分也发生了巨大变化，除了国有专业模具厂外，集体、合资、独资和私营也得到了快速发展。近年许多模具企业加大了用于技术进步的投资力度，将技术进步视为企业发展的重要动力。一些国内模具企业已普及了二维CAD，并陆续开始使用UG、Pro/Engineer、I-DEAS、Euclid-IS等国际通用软件，个别厂家还引进了Moldflow、C-Flow、DYNAFORM、Optris和MAGMASOFT等CAE软件，并成功应用于冲压模的设计中。以汽车覆盖件模具为代表的大型冲压模具的制造技术已取得很大进步，东风汽车公司模具厂、一汽模具中心等模具厂家已能生产部分轿车覆盖件模具。此外，许多研究机构和大专院校开展模具技术的研究和开发。经过多年的努力，在模具CAD/CAE/CAM技术方面取得了显著进步；在提高模具质量和缩短模具设计制造周期等方面做出了贡献。

1.1未来冲压模具制造技术发展趋势

模具技术的发展应该为适应模具产品“交货期短”、“精度高”、“质量好”、“价格低”的要求服务。达到这一要求急需发展如下几项：

(1)全面推广CAD/CAM/CAE技术模具CAD/CAM/CAE技术是模具设计制造的发展方向。随着微机软件的发展和进步，普及CAD/CAM/CAE技术的条件已基本成熟，各企业将加大CAD/CAM技术培训和技术服务的力度；进一步扩大CAE技术的应用范围。计算机和网络的发展正使CAD/CAM/CAE技术跨地区、跨企业、跨院所地在整个行业中推广成为可能，实现技术资源的重新整合，使虚拟制造成为可能。

(2)高速铣削加工国外近年来发展的高速铣削加工，大幅度提高了加工效率，并可获得极高的表面光洁度。另外，还可加工高硬度模块，还具有温升低、热变形小等优点。高速铣削加工技术的发展，对汽车、家电行业中大型型腔模具制造注入了新的活力。目前它已向更高的敏捷化、智能化、集成化方向发展。

   (3)模具扫描及数字化系统高速扫描机和模具扫描系统提供了从模型或实物扫描到加工出期望的模型所需的诸多功能，大大缩短了模具的在研制制造周期。有些快速扫描系统，可快速安装在已有的数控铣床及加工中心上，实现快速数据采集、自动生成各种不同数控系统的加工程序、不同格式的CAD数据，用于模具制造业的“逆向工程”。模具扫描系统已在汽车、摩托车、家电等行业得到成功应用，相信在“十五”期间将发挥更大的作用。?

   (4)电火花铣削加工电火花铣削加工技术也称为电火花创成加工技术，这是一种替代传统的用成型电极加工型腔的新技术，它是有高速旋转的简单的管状电极作三维或二维轮廓加工(像数控铣一样)，因此不再需要制造复杂的成型电极，这显然是电火花成形加工领域的重大发展。国外已有使用这种技术的机床在模具加工中应用。预计这一技术将得到发展。

   (5)提高模具标准化程度我国模具标准化程度正在不断提高，估计目前我国模具标准件使用覆盖率已达到30%左右。国外发达国家一般为80%左右。

   (6)优质材料及先进表面处理技术选用优质钢材和应用相应的表面处理技术来提高模具的寿命就显得十分必要。模具热处理和表面处理是否能充分发挥模具钢材料性能的关键环节。模具热处理的发展方向是采用真空热处理。模具表面处理除完善应发展工艺先进的气相沉积(TiN、TiC等)、等离子喷涂等技术。?

   (7)模具自动加工系统的发展这是我国长远发展的目标。模具自动加工系统应有多台机床合理组合；配有随行定位夹具或定位盘；有完整的机具、刀具数控库；有完整的数控柔性同步系统；有质量监测控制系统。

1.2 模具技术发展的几个特点

模具与压力机是决定冲压质量、精度和生产效率的两个关键因素。先进的压力机只有配备先进的模具，才能充分发挥作用，取得良好效益。模具的发展方向为：

1.2.1 以计算机为中心

计算机技术的广泛使用，使现代模具企业的首要特征是以计算机为中心。计算机是整个企业最活跃、最核心，最需要投资以及更新最快的部分(其软件每2-3年、硬件每3-5年更新一次)。以计算机为中心建立起来的计算机辅助设计、计算机辅助工程以及计算机辅助制造(CAD/CAE/CAM)是企业的生产主线，并向集成化、网络化、智能化方向发展。

1.2.2 模具设计水平高

现代模具企业都广泛采用计算机辅助技术、人工智能技术进行设计决策、模拟分析和优化设计。同时，数据库和计算机网络技术应用使设计师可以在更大范围内共享设计资料、信息、资源和展开合作，使其现代模具设计的总体水平上升到一个前所未有高度。现代模具有的还要求有控压、控温等功能，甚至要求提供某些测量元件。在模具标准化、通用化、典型化程度很高的情况下，各模具企业都利用自己的某些专长设计制造模具，在激烈的竞争中求发展。

1.2.3 生产设备先进

现代模具的加工，更多地依靠各种自动化程度较高的高精度、高效率机床。从模具粗加工、热处理到各种精加工、光整加工、质量控制与检测，必须设备齐全，配套合理。其中，数控加工设备所占比重比较大，以适应单件或小批量复杂模具的生产。同时，数控加工设备也是模具CAD/CAE/CAM的基础，有助于实现模具制造的全自动加工。另外还有：

（1）供货期短。现代模具对短交货期的要求日益迫切，模具的交货期限已从传统的几个月向几十天、十几天甚至数小时发展，这些是传统制模方法所不能达到的。模具设计已从人工经验设计方式转化为依靠计算机辅助设计的方式。广泛采用模具CAD/CAE/CAM技术，使模具设计、计算机分析、生产装备、数控加工、检验、试模等工作一体化，设计数据直接经过网络和数据库管理系统传递到各个生产部门，大大缩短模具生产周期。此外，成形过程计算机模拟，并行工程、人工智能，快速原型制造等先进制造技术的应用，以及模具标准化、专业化生产等也为缩短供货期起了重要作用。

（2）重视人才培养和汇聚。一个现代模具企业，最重要的就是拥有丰富的经验和掌握先进技术与设备的人。当前，高素质、高技艺的模具人才的缺乏已成为全球性的紧迫问题，加强这方面人才的培养和再教育，并将这些人才成功地汇聚在一起，就成为现代模具企业的重要任务和特征。

1.3 我国锻压工业的现状及发展对策

目前我国主要汽车生产厂，约有90%的冲压线采用一台双动拉伸压力机（或多连杆单动拉伸压力机）和4-6台单动压力机组成冲压流水线，手工上下料完成大型覆盖件的冲压生产，生产效率低，生产节拍最高只有3-5次/分；人身安全和工件环境差；在手工上下料和传送工件过程中，易造成工件划伤等缺陷，冲压制件质量差；整条冲压线长60米左右，约需20-24名操作工人，占地面积大，人工成本高，冲压件制造成本比国外高2-3倍，是我国汽车工业严重缺乏市场竞争力的重要因素之一。我国有90%的冲压线采用人工上下料，另有10%的冲压线实现了单机联线自动化，生产节拍最高为6-8次/分，而代表当今冲压技术国际水平的大型多工位压力机，在我国汽车工业中的应用仍是空白。这也是我国冲压行业与西方发达国家的主要差距所在，在很大程度上制约了我国汽车工业的发展。

   随着我国工业技术水平的发展，特别是以轿车为代表的汽车工业快速发展，带动汽车零件的产量和质量不断提高。但必须清醒地认识到，中国与国际先进水平仍有很大差距，而且随着加入WTO，国际大汽车公司必然严重冲击中国汽车工业，国内同行之间的竞争也将日趋激烈。中国汽车工业的发展，离不开装备工业的大力支撑，锻压设备制造业必须满足汽车工业大批量生产的要求，向自动化、高效率方向发展。

2  零件工艺性分析

2.1 冲裁工艺性

冲裁件的工艺性是指冲裁件对冲压工艺的适应性，即冲裁件的结构形状、尺寸大小、精度等级是否符合冲裁加工的工艺要求。良好的结构工艺性应保证材料消耗少，工序数目少，模具结构简单而寿命高，产品质量稳定，操作简单单等等。通常对冲裁件的工艺性影响最大的是几何形状尺寸和精度要求。对几何形状的要求是冲裁件的形状应尽可能简单、对称，最好采用圆形、矩形等规则的几何形状或由这些形状所组成，使排样时废料最少；冲裁件的凸出悬臂和凹槽的宽度不宜太小，以免凸模折断；冲裁件的外形或内形的转角出，要避免夹角出现，应以圆弧过渡，以便于模具加工，减少热处理或冲压时的在尖角处开裂的现象，同时可以防止尖角部位的刃口磨损过快而使模具寿命降低。对精度的要求是冲裁件的经济精度一般不高于IT11级，最高可达

IT8~10级，冲孔比落料的精度约高一级。

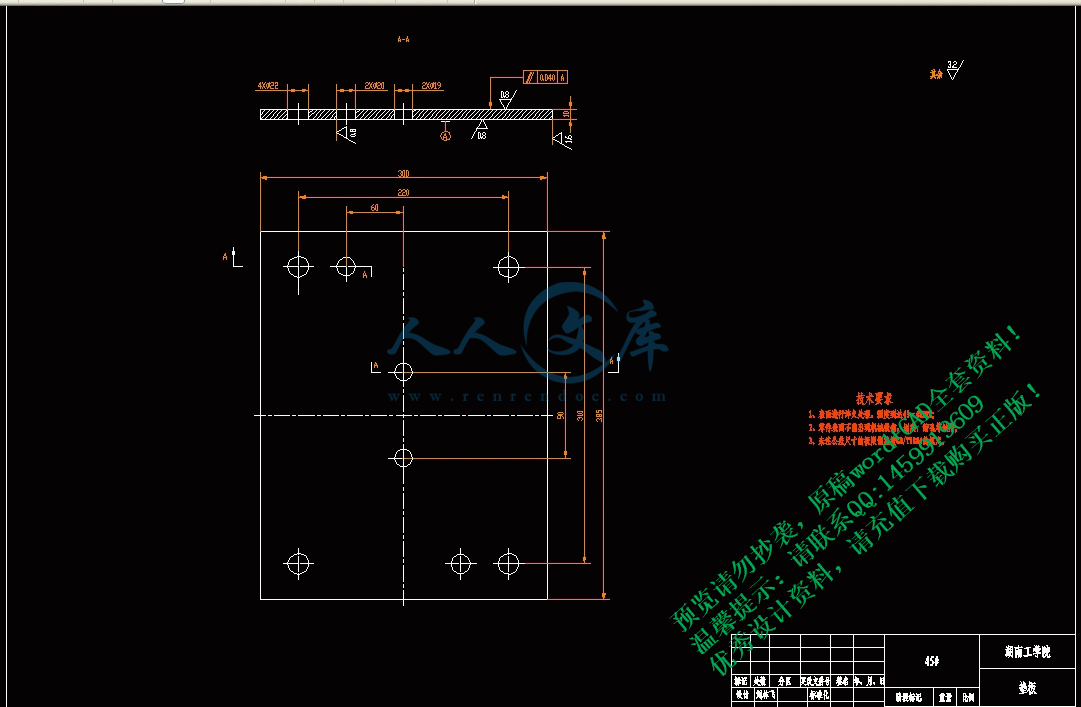
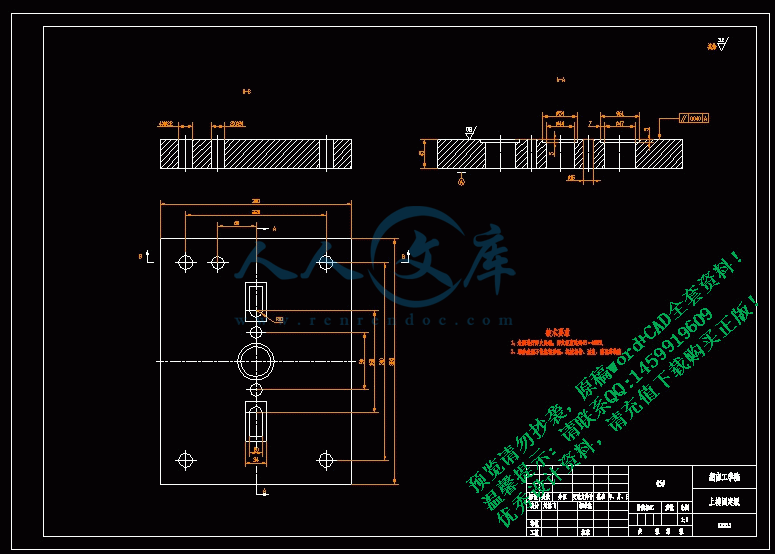
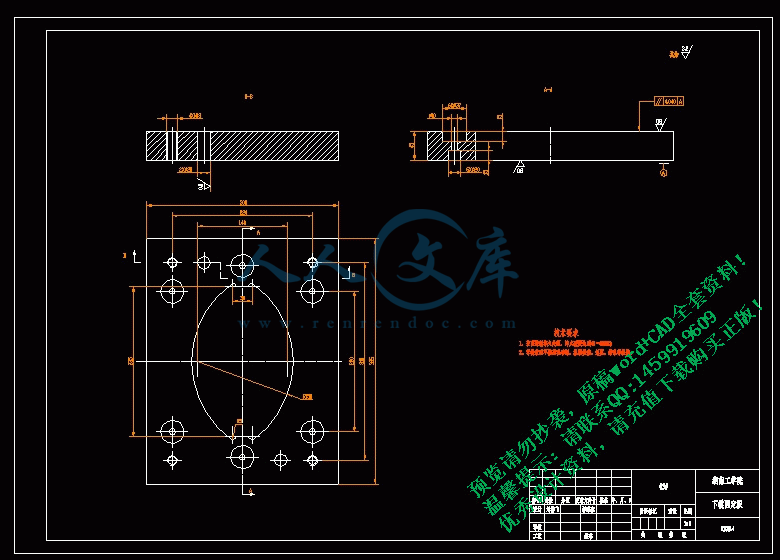
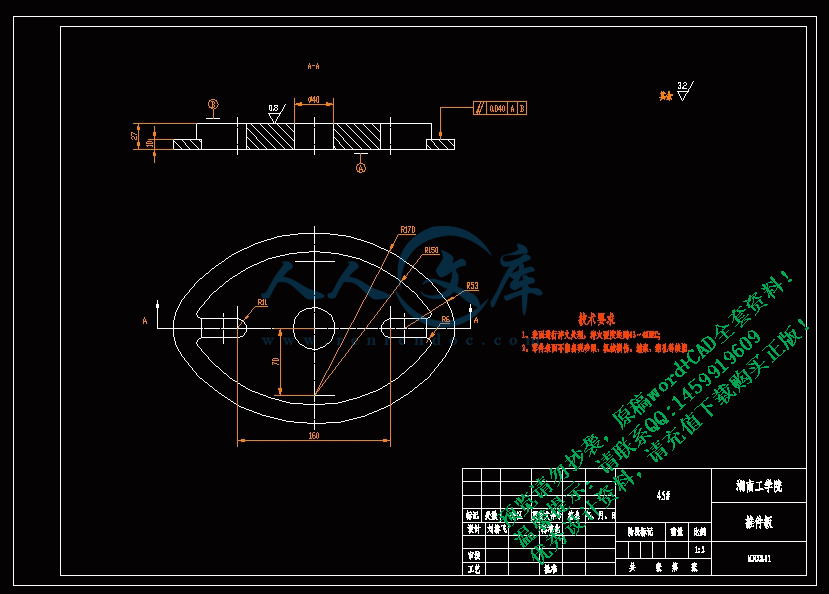
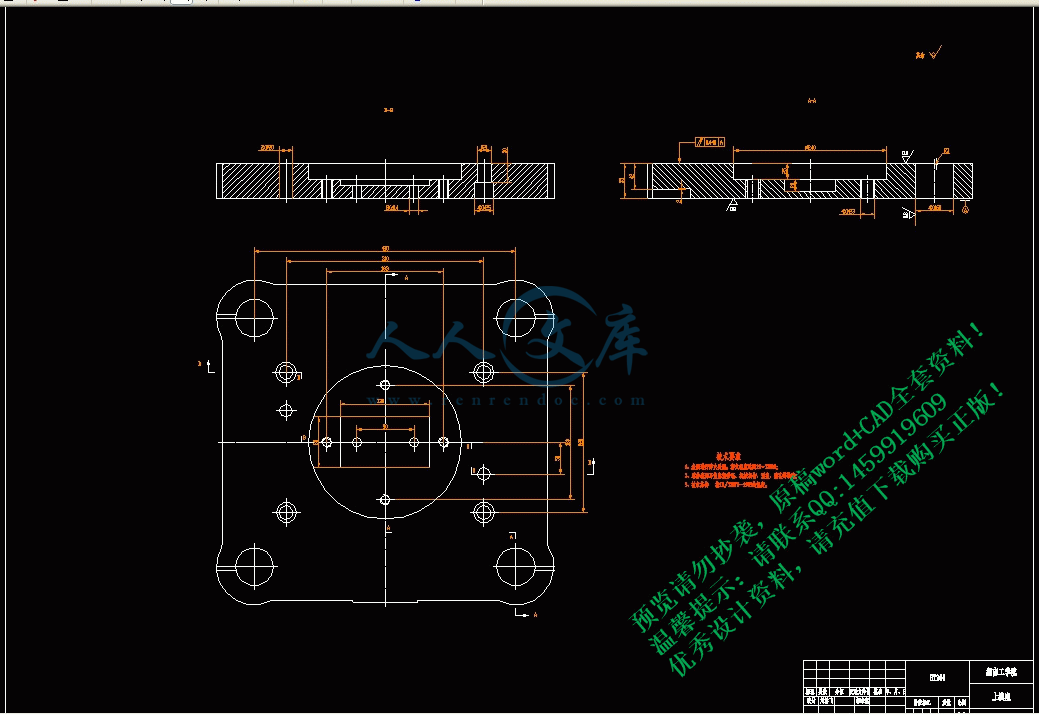
该零件的形状如图1.1，其冲裁工艺性为：

2.1.1 结构与尺寸

该零件结构较简单，形状对称，尺寸较大，冲孔Φ40，一般冲孔模对该种材料可以冲压的最小孔径d≥t, t=2mm＜d=40mm.因而Φ20孔符合工艺要求。

对于孔中心距100±0.27mm，较高精度模具可以达到两孔中心距公差为±0.06。最小孔边距b≥25mm,b1≥30mm..由零件图可知各孔边距均大于最小孔边距。

以上分析均符合冲裁工艺要求。

参考文献

[1]  刘心冶主编. 冷冲压工艺及模具设计［Ｍ］. 重庆：重庆大学出版社，1998.1~56 Liu xinyeeditor. Cold stamping and die design processes［Ｍ］. Chongqing : Chongqing University Press, 1998.1~56(in Chinese)

[2]  何忠保,陈晓华 王秀英编. 典型零件模具图册［Ｍ］.北京. 机械工业出版社，2000.25~27

He zhongbao, Chen iaohua ,Wang xiuying series. Typical parts molding atlas［Ｍ］. Beijing. Machinery Industry Press, 2000.25~27(in Chinese)

[3]  徐政坤主编. 冲压模具设计与制造［Ｍ］. 北京：化学工业出版社，1999.12~156

xu zhengkun editor. Stamping die design and manufacture［Ｍ］. Beijing : Chemical Industry Press, 1999.12~156(in Chinese)

[4]  模具实用技术丛书编委会编. 冲模设计应用实例［Ｍ］. 北京：机械工业出版社，2002.50~120

Advanced series of practical technical editor series. Application templates design examples［Ｍ］. Beijing : Machinery Industry Press, 2002 (in Chinese)

[5]  史铁梁主编. 模具设计指导［Ｍ］. 北京：机械工业出版社，1993.2~75

  shi teliang editor. Advanced design guidance［Ｍ］. Beijing : Machinery Industry Press, 1993.23~145(in Chinese)

[6]  王新华 袁联富编. 冲模结构图册［Ｍ］. 北京：机械工业出版社，2003.23~145

wang Xinhua ,Yuan lianFu series. Dies structure atlas［Ｍ］. Beijing : Machinery Industry Press, 2003.23~145(in Chinese)

[7]  冯柄尧等编. 模具设计与制造简明手册［Ｍ］. 上海：上海科学技术出版社，1998.2~90

hong bingrao such series. Advanced design and manufacture concise manual［Ｍ］. Shanghai : Shanghai Science and Technology Press, 1998.150~205(in Chinese)

[8]  王树勋、高广升编. 冷冲压模具结构图册大全［Ｍ］. 广州：华南理工大学出版社，1988.23~130

Wangshuxun, gaoguangsheng series. Cold stamping die structure Atlas Book［Ｍ］. Guangzhou : South China Science and Technology University Press, 1988.70~144(in Chinese)

[9]  李硕本主编. 冲压工艺学［Ｍ］. 北京：机械工业出版社，1982.65~320

lishuoben editor. Ram crafts Technological Sciences［Ｍ］. Beijing : Machinery Industry Press, 1982.23~145(in Chinese)

[10]  郑家贤编著. 冲压工艺模具设计实用技术［Ｍ］. 北京：机械工业出版社，1999.240~360

 zhengjiaxian author. Stamping die design processes practical technology［Ｍ］. Beijing : Machinery Industry Press, 1999.310~405(in Chinese)


内容简介：
任务书系： 机械工程系 专业： 材料成型及控制工程指导教师和道学生姓名刘林飞课题名称空气滤清器连接板冲孔、冲槽、落料复合模设计内容及任务设计图纸模具总装图一张全部模具零件图纸（其中至少有一张电脑绘图）所有图纸折合成0号图不得少于3张。设计说明书1、资料数据充分，并标明数据出处。2、计算过程详细、完全。3、公式的字母含义应标明，有时还应标注公式的出处。4、内容条理清楚，按步骤书写。5、说明书要求用计算机打印。6、设计说明书按要求格式独立撰写，不少于12000字。自选一个重要模具零件编制加工工艺路线，进行相关的计算，并编制加工工艺卡和工序卡。翻译一篇本专业外文文献（10000个以上印刷符号），并附译文。拟达到的要求或技术指标1、保证规定的生产率和高质量的冲压件的同时，力求成本低、模具寿命长。2、设计的冷冲模必须保证操作安全、方便。3、冲模零件必须具有良好的工艺性，即制造装配容易、便于管理。4、便于搬运、安装、紧固到冲床上并且方便、可靠。5、保证模具强度前提下，注意外形美观，各部分比例协调。进度安排起止日期工作内容备注2周（2.283.11）毕业调研2周（3.143.25）集中实习10周（3.286.3）毕业设计1周（6.66.10）毕业答辩主要参考资料、冷冲压工艺及模具设计刘心治主编重庆大学出版社、冲压工艺及模具设计万战胜主编 铁道出版社、冲模设计 吉林人民出版社、实用冲压技术 机工出版社、冷冲压及塑料成型工艺与模具设计资料 机工出版社、模具设计与制造简明手册 冯炳尧等编 上海出版社7、冲压工艺模具设计实用技术郑家贤编机械工业出版社8、实用板金冲压工艺图集梁炳文主编机械工业出版社9、几何量公差与检测甘永立主编上海科学技术出版社10、机械制造专业英语章跃主编机械工业出版社教研室意见年 月 日系主管领导意见年 月 日零件号材料T10A毛坯重量编制机械加工工艺过程综合卡片零件名称冲孔凸模生产类型毛坯种类指导工序工序名称工序说明机床夹具刀具量具切削深度mm进给量mm/r主轴转速r/min切削速度m/min时间定额min5下料根据零件图尺寸，下料F20360mm10车外圆面车右端面，粗车外圆柱面尺寸：F10.6324，F14.4318，F1735，调头车外圆F638CA6140三爪卡盘外圆车刀游标卡尺4.70.8150031.415检验20热处理按技术要求热处理至HRC586225精车精车F10.15mm至尺寸，并车出斜度309CA6140三爪卡盘外圆车刀游标卡尺0.170.8150016.630磨外圆面磨F14至尺寸外圆磨床三爪卡盘砂轮游标卡尺0.20.00560027.135钳工去除工艺柄40检验Discrete Applied Mathematics 98 (1999) 121130Pattern minimisation in cutting stock problemsColin McDiarmidDepartment of Statistics, University of Oxford, 1 South Parks Road, Oxford OX1 3TG, UKReceived 21 October 1997; accepted 8 February 1999AbstractIn the cutting stock pattern minimisation problem, we wish to satisfy demand for variouscustomer reels by cutting as few as possible jumbo reels, and further to minimise the numberof distinct cutting patterns used. We focus on the special case in which any two customer reels?t into a jumbo, but no three do: this case is of interest partly because it is the simplest casethat is not trivial, and partly because it may arise in practice when one attempts to improve asolution iteratively.We ?nd that the pattern minimisation problem is strongly NP-hard even in this special case,when the basic problem of ?nding a minimum waste solution is trivial. Our analysis focusseson balanced subsets, and suggests an approach for heuristic methods involving searching forbalanced subsets. ? 1999 Elsevier Science B.V. All rights reserved.Keywords: Cutting stock; Cutting patterns; Partition; NP-hard; Dynamic programming1. IntroductionSome materials such as paper may be manufactured in wide jumbo rolls, whichare later cut into much narrower rolls to satisfy customer demands. To minimise waste,cutting patterns should be chosen so as to use as few jumbos as possible (see 4,7,8).Thus the basic cutting stock problem has input a positive integer J, distinct positiveintegers r1;:;rn, and positive integers d1;:;dn; and the required task is to use as fewas possible jumbos of width J to satisfy the demand for dicustomer reels of width ri,for each i=1;:;n. This is one of the classical OR problems. It contains the stronglyNP-complete problem 3-PARTITION: thus it is NP-hard even if the jumbo size J isbounded by a polynomial in n, and each customer reel size risatis?es J=4riJ=2 see 6, p. 224. Thus we cannot expect always to be able to ?nd optimal solutionsto such problems within a reasonable time.Fax: +44-1865-272-595.E-mail address: cmcdstats.ox.ac.uk (C. McDiarmid)0166-218X/99/$-see front matter ? 1999 Elsevier Science B.V. All rights reserved.PII: S0166-218X(99)00112-2122C. McDiarmid/Discrete Applied Mathematics 98 (1999) 121130Each time a di?erent pattern of customer reels is to be cut, the knives on the cuttingmachine need to be re-set. A problem presented by C.N. Goulimis and investigatedat the 29th European Study Group with Industry in March 1996 concerned how to?nd solutions to the above cutting stock problem, that further minimise the numberof distinct cutting patterns used see 1,2,9. This is of course going to be hard ingeneral, since the basic problem is hard. In order to investigate the added di?culty ofthe extended problem, we consider here a special case in which the basic problem ofminimising the number of jumbos (minimising waste) is trivial.PATTERN MINIMISATIONInput: positive integers d1;:;dn.Task: in the cutting stock problem where the demand is for direels of type i, andany two reels ?t into a jumbo but no three do, ?nd a minimum waste solution whichfurther minimises the number of distinct patterns used.This very restricted special case is of interest partly because it seems to be thesimplest case that is not completely trivial, and partly because it may arise in practicewhen one attempts to improve a solution iteratively. For example, if a collection ofsome of the currently used patterns agree on the large reels and di?er only on smallreels, and any two small reels ?t in the width left by the large reels, then whenwe attempt to re-allocate the small reels we face exactly this special case 16. Weinvestigate whether the pattern minimisation problem remains hard in this special case,and brie?y consider approaches to ?nding good solutions.It is clear that the least number of jumbos needed is dPidi=2e, the round up of halfthe total demand; and it is trivial to ?nd a corresponding minimum waste solution. But,how easy is it to ?nd, amongst the minimum waste solutions, one which minimises thenumber of patterns used? For the variant of the problem when no three customer reels?t into a jumbo but also some pairs may not, it was shown in 1 that the problem isstrongly NP-hard. The theorem below strengthens this negative result.Theorem 1. The problem PATTERN MINIMISATION is strongly NP-hard.The key to understanding the above problem is the concept of a balanced subset.Given a family d =(d1;:;dn) of non-negative integers, denote by ?(d) the minimumnumber of patterns used in any minimum waste solution. Also, call a non-empty subsetof 1;:;n balanced if it can be partitioned into two sets A and B such thatPiAdi=PiBdi. Thus if some di= 0 then the singleton set i is balanced. Let ?(d) be themaximum number of pairwise disjoint balanced subsets.Lemma 1. IfPidiis even; then ?(d) = n ?(d).IfPidiis odd, then ?(d)=?(d0), where d0is obtained from d by adding an extraco-ordinate dn+1= 1. We shall prove this lemma in the next section.C. McDiarmid/Discrete Applied Mathematics 98 (1999) 121130123When faced with a pattern minimisation problem, we are led by Theorem 1 andLemma 1 above to consider heuristic approaches to ?nding good packings of balancedsubsets. Unfortunately it is NP-complete even to test if a given family a1;:;anofpositive integers has a balanced subset. This is the problem called WEAK PARTITIONis David Johnsons NP-completeness column 10, where three independent proofs ofits NP-completeness are cited, the earliest being in 13.We wish to ?nd a good packing of balanced subsets, but we know that it is veryhard to ?nd a best packing, and indeed it is hard to ?nd any balanced subset. A naturalheuristic approach is repeatedly to seek and delete a balanced subset, preferably a smallone. One method for seeking a balanced subset is to use di?erencing, where we repeat-edly replace two numbers by the absolute value of their di?erence see 5,12,15,17.This approach is currently being investigated in the context of pattern minimisation 16.Another method is to use a tolerably fast algorithm that is guaranteed to ?nd a balancedsubset or a smallest balanced subset: we shall see that we can use a straightforwarddynamic programming method to test if there is a balanced subset, and ?nd a smallestbalanced subset if there is one, in pseudo-polynomial time. Heuristic approaches formore general cases of pattern minimisation in cutting stock problems are considered in1,2,9,11.The plan of the rest of the paper is as follows. In the next section we establishthe relationship between numbers of patterns and packings of balanced subsets. Nextwe prove our main result, that the problem PATTERN MINIMISATION is stronglyNP-hard. After that, we consider brie?y how to search for balanced subsets, and ?nallywe make a few concluding remarks.2. Patterns, degrees and balanced setsIn this section we shall prove Lemma 1, which relates numbers of patterns to pack-ings of balanced subsets. The problem PATTERN MINIMISATION can be rephrasedin terms of graphs. A pattern involving reel type i and reel type j will correspond toan edge between vertex viand vertex vj. We shall allow our graphs to contain a loopat any vertex but not to contain multiple edges.Given a graph G = (V;E) on the vertex set V = v1;:;vn, together with a familyw of non-negative integer weights weon the edges e, the weighted degree of vertex viis the sum over the edges e incident with viof the weight we, with any loop countingtwice. Given a vector d = (d1;:;dn) of positive integers, we call the pair G;w arepresenting network for d if each vertex vihas weighted degree di. Consider thefollowing problem.DEGREESInput: positive intergers d1;:;dnwithPidieven.Task: ?nd a representing network with as few edges as possible.124C. McDiarmid/Discrete Applied Mathematics 98 (1999) 121130Given a family d =(d1;:;dn) of positive integers withPidieven, there is a naturalcorrespondence between the solutions in DEGREES and those in PATTERN MINIMI-SATION, and in particular the minimum number of edges possible in the former equals?(d).Proof of Lemma 1. Suppose thatPidiis even. Let G;w be any representing net-work, and consider a component of G with set K of k nodes. It must of coursehave at least k 1 edges, and if it has this number and thus is a tree on K, thenthe two-colouring of the vertices show that K is balanced. Thus the number of edgesin G is at least n minus the number of components on balanced sets. Hence?(d)n ?(d).To prove the reverse inequality, consider any partition of v1;:;vn into sets(Ki: i I) of which at most one is not balanced. We will show that there is rep-resenting network G;w such that the graph G has components (Gi: i I) where Gihas vertex set Ki, and these components are such that, if Kiis balanced then Giis atree and if not then Giis a tree with one added loop. This will complete the proof ofthe lemma.Consider a balanced set K, with partition A B such thatPiAdi=PiBdi. Wemust show that there is a tree T on K and non-negative weights weon the edges eof T such that, for each node v K, the sum of the weights of the incident edgesequals dv(where loops count double). We use induction on |K|. If either A or Bis empty, the result is trivial, since we must have dv= 0 for each v K. Supposethen that both A and B are non-empty. Pick any a A and b B, and withoutloss of generality suppose that dadb. Reduce daby db. Now K b is balanced,and inductively we can ?nd an appropriate weighted tree. Then add the edge ab withweight db.Finally, consider a set K which is not balanced, but is such that the correspondingsum of demands is even. As above, we can always replace two demands by theirdi?erence at the cost of using one edge. Thus we can satisfy all but one demand byusing edges forming a tree on K, and then one added loop completes the component.3. PATTERN MINIMISATION is strongly NP-hardIn this section we prove Theorem 1, that the problem PATTERN MINIMISATION isstrongly NP-hard. A summing triple (or Schur triple) is a set of three distinct integerssuch that the sum of two equals the third. The following problem could be more fullydescribed as partition of distinct integers into summing triples.SUMMING TRIPLESInput: distinct positive integers s1;:;s3n.Question: can the input be partitioned into summing triples?C. McDiarmid/Discrete Applied Mathematics 98 (1999) 121130125This problem is similar to NUMERICAL MATCHING WITH TARGET SUMS inGarey and Johnson 6, p. 224, but with the extra (surprisingly troublesome) conditionthat the numbers involved must be distinct.Lemma 2. The problem SUMMING TRIPLES is strongly NP-complete.Most of this section will be devoted to proving the above lemma, but ?rst let us seethat it will yield Theorem 1.Proof of Theorem 1 (assuming Lemma 2). We give a strightforward polynomial timereduction of SUMMING TRIPLES to DEGREES. Consider an instance of SUMMINGTRIPLES as above. Take d = (2s1;:;2s3n) as an instance of DEGREES. Since thesiare distinct positive integers, there are no balanced sets of size less than 3. Thus?(d)6n. Hence by Lemma 1, ?(d)2n and ?(d)=2n if and only if s1;:;s3ncan bepartitioned into summing triples.Now consider the problem SUMMING TRIPLES, which is clearly in NP. We shallshow that it is strongly NP-complete by giving a reduction from the NP-completeproblem RESTRICTED X3C, described below, to SUMMING TRIPLES with eachinterger siin O(n3).RESTRICTED X3CInput: a set X of 3q elements and a collection C of triples contained in X, suchthat each element of X is in exactly 3 triples.Question: can X be partitioned into triples in C?Lemma 3. The problem RESTRICTED X3C is NP-complete.Proof. It is known that the problem is NP-complete if each element is constrained tobe in at most 3 triples rather than exactly 3 see Garey and Johnson 6, p. 221. Itis easy to tidy up an instance X;C so that each element is in exactly 3 triples.Clearly we can insist that each element is in either 2 or 3 triples. We can partitionthe elements which are in exactly two triples into blocks of size three. For each blockx;y;z, add three new elements x0;y0;z0and four new triples x;y0;z0; x0;y;z0;x0;y0;z; x0;y0;z0. Call the new instance X0;C0. Clearly, each element of X0is inexactly 3 triples in C0; and X can be partitioned into triples in C if any only if X0can be partitioned into triples in C0.Proof of Lemma 2. Consider an instance X;C of RESTRICTED X3C, where |X| =|C| = 3q = n. Let Y = X 1;:;7. We shall construct an expanded collectionD of triples contained in Y, such that X can be partitioned into triples in C if andonly if Y can be partitioned into triples in D; and then we shall construct an instance(s(y): y Y) of SUMMING TRIPLES, where each size s(y) is O(n2), such that thesumming triples correspond precisely to the triples in D.126C. McDiarmid/Discrete Applied Mathematics 98 (1999) 121130Form a bipartite graph G = (C;X;E) with vertex parts C and X and with verticesT C and x X adjacent (that is, edge T x E) exactly when x T. Since eachvertex degree in G is three, we may ?nd in polynomial time a proper 3-edge-colouring? : E 1;2;3. We now split each element x X into three copies (x;1);(x;2) and(x;3). Given a triple T = x;y;z C, let T0be the tripleT0= (x;?(Tx);(y;?(Ty);(z;?(Tz):Observe that the elements in the triple T0have distinct ?rst co-ordinates (in X), anddistinct second co-ordinates (which must be 1,2,3); and that the family C0=(T0: T C)partitions the set X 1;2;3.Next, for each x X, let Fxbe the collection consisting of the four triples (x;1),(x;4);(x;5); (x;3);(x;4);(x;5); (x;2);(x;6);(x;7) and (x;3);(x;6);(x;7). Let Dbe the collection consisting of C0together with all the triples in the collections Fxforx X. Thus D contains |C| + 4|X| = 5n triples.If some subcollection D0of D is a partition of Y, then for each x X, exactly oneof the elements (x;1);(x;2);(x;3) is not covered by triples in D0 Fxand so must becovered by triples in D0C0. It follows easily that X may be partitioned into triples inC if and only if Y may be partitioned into triples in D. This completes the ?rst partof the construction.Next we shall see how to assign a size s(y) to each element y Y so that thesumming triples of elements in Y are precisely the triples in D. We shall use a familyof almost k-wise independent random variables de?ned on a small sample space.Let l=d3 log2ne+10, let t=2nl, let k=9l, and let ?=12. There is a subset ? of 0;1t,of size 2(1+o(1)k, with the following property: if a point ! = (!1;:;!t) is pickeduniformly at random from ?, then (!1;:;!t) is ?-away from k-wise independent see 3. Further such a set ? can be (explicitly) constructed in time bounded by apolynomial in n.Given a point ! ?, for each i = 1;:;2n, let Si= Si(!) be the non-negative in-teger with binary expansion !(i1)l+1!il. When a point ! = (!1;:;!t) is pickeduniformly at random from ?, then S1;:;S2nare random variables, taking valuesin 0;1;:;N 1, where N = 2l, and they have the following property. For anyI 1;:;2n with 0|I|69, and for any set E 0;1;:;N 1I, we have|P(Si: i I) E) |E|=N|I|61=2:We can now de?ne the element sizes s(y) for our instance of SUMMING TRIPLES.For clarity we shall write s(x;1) rather than s(x;1) and so on. Enumerate the elementsof X as x1;x2;:;xn. Given a sample point ! ?, for each i=1;:;n we let s(xi;1)=2S2i1(!) + 2N and s(xi;2) = 2S2i(!) + 2N. Let x X. Suppose that (x;3) is in thetriple T0 C0, where T0also contains (x0;1) and (x00;2). Then we let s(x;3)=s(x0;1)+s(x00;2) (4N). This de?nes s(x;i) for each x X and i 1;2;3. Now, for eachx X, let s(x;4) = (s(x;1) + s(x;3)=2, s(x;5) = (s(x;1) + s(x;3)=2;s(x;6) = (s(x;2)+s(x;3)=2, and s(x;7)=(s(x;2)+s(x;3)=2. We have now de?ned a positive integersize s(y) for each y Y, and each triple in D is always summing.C. McDiarmid/Discrete Applied Mathematics 98 (1999) 121130127Let B? be the bad event that either the values s(y) for y Y fail to be distinct,or some triple other than those in D is summing. We shall show that P(B)1. Itwill follow that there is a sample point ! ? B, and we can ?nd such a point inpolynomial time by exhaustive search. This will then complete the proof of the lemma.To prove that P(B)1, it su?ces for us to suppose that the random variablesS1;:;S2nare precisely 9-wise independent, with each uniformly distributed on0;1; :;N1, and then to prove that P(B)1=2. Observe that, from the de?nitionof s(y), for each y there is a vector a(y)1;0;1;22n, with support of size at most3, such that s(y)Pia(y)iSiis a constant (that is, does not depend on !).Let y1and y2be distinct elements of Y. Let a = a(y1) a(y2). It is easy to seethat a is a non-zero integer vector with support of size at most 6, and there is aconstant c such that s(y1) = s(y2) if and only ifPiaiSi= c. But the probability ofthis last event is at most 1=N. Thus the probability that the values s(y) for y Y arenot all distinct is at most?|Y|2?1N6(7n)22N.We may argue similarly for the unwanted triples. Let y1;y2and y3be distinctelements of Y, which form a triple T which is not in D. Consider the event thats(y1) + s(y2) = s(y3). Let a = a(y1) + a(y2) a(y3). Then a has support of size atmost 9, and there is a constant c such that s(y1)+s(y2)=s(y3) if and only ifPiaiSi=c.We claim that the vector a is non-zero. It will then follow that the probability that sometriple not in D is summing is at most?|Y|3?31N6(7n)32N; and hence P(B)6(7n)2(8n)210n31=2,as required.It remains only to establish the above claim. For each element y = (x;i) Y, let?1(y)=x and ?2(y)=i. Also, denotePia(y)iby ?(y). Assume that a =0: we mustobtain a contradiction. Note ?rst that if ?2(y)=3 then ?(y)=4. Hence neither ?2(y1)nor ?2(y2) can equal 3, since we would than havePiai4 ?(y3)0.Now suppose that ?2(y1) 1;2, that is ?(y1) = 2. Then ?(y2) must be 1 or 2.We consider these two cases.(i) Suppose ?rst that ?(y2)=1. Then ?(y3)=3. Now a(y1) has only one non-zeroco-ordinate 2, a(y2) has 1;1;1 and a(y3) has 1;1;1. Then ?1(y1) = ?1(y2) = ?1(y3)and the triple T = (y1;y2;y3) is in D, a contradiction.(ii) Now suppose that ?(y2) = 2. Then ?(y3) = 4. Now a(y1) has one 2, a(y2) hasone 2 and a(y3) has 2,2. Again the triple T is in D, a contradiction.We have now shown that ?2(y1) 6 1;2;3, and similarly for y2. Thus both ?2(y1)and ?2(y2) are in 4;5;6;7. So ?(y1) and ?(y2) are 1 or 3, and ?(y3) is 2 or 4.Suppose ?rst that ?(y1) = ?(y2) = 1, and so ?(y3) = 2. Then both a(y1) and a(y2)have non-zero co-ordinates 1;1;1 and a(y3) has one 2. But then a(y1) and a(y2)must have the same support. It follows that ?1(y1) = ?1(y2), and this is not possible.Without loss of generality, we may now assume that ?(y1) = 1 and ?(y2) = 3.Then ?(y3) = 4; and a(y1) has non-zero co-ordinates 1;1;1; a(y2) has 1;1;1; anda(y3) has 2,2. Then again we ?nd that a(y1) and a(y2) must have the same support,and so ?1(y1) = ?1(y2) = ?1(y3). But now the triple T is in D, a contradiction.128C. McDiarmid/Discrete Applied Mathematics 98 (1999) 1211304. Finding balanced subsetsWe noted earlier that it is NP-complete to test if a given family a1;:;anof pos-itive integers has a balanced subset, but that we may nevertheless wish to search forbalanced subsets in certain heuristic approaches to pattern minimisation. In this sectionwe see that a straightforward approach based on dynamic programming will solve suchproblems in pseudo-polynomial time.We ?rst see how to test if there is a balanced subset, and if so to ?nd one (withsmallest corresponding sum), in O(nPiai) steps. After that we shall see how to ?nda smallest balanced subset, in O(n2Piai) steps. It is not obvious which of thesealgorithms would be better within a heuristic method for pattern minimisation.Let s0=Piai=2. For each s = 0;1;:;s0, and each j = 0;1;:;n, let f(s;j) beT if there is a subset of 1;:;j with corresponding sum s, and let f(s;j) equal Fotherwise. Then f(0;j)=T for each j=0;1;:;n, and f(s;0)=F for each s=1;:;s0.We can calculate all the values f(s;j) in turn, in O(1) steps per value, as follows.for s = 1;:;s0for j = 1;:;nf(s;j) f(s;j 1) f(s aj;j 1):(If s0 we interpret f(s;j) as F.)If, in the recurrence above, it is never the case that both terms on the right are T, thenthere is no balanced subset. But suppose that this case does occur, and the ?rst time wemeet it is at s0;j0. Then there are two distinct subsets A and B with corresponding sums (one containing j0and one not). Further A and B must be disjoint, by the minimalityof s0. Clearly we can ?nd such sets A and B quickly, and their union is the desiredbalanced set.Now suppose that we wish to ?nd a smallest balanced subset if there is one. Wedescribe a method based on dynamic programming which takes O(n2Piai) steps.As before, let s0=Piai=2. For each s=0;1;:;s0, and each j;k=0;1;:;n with k6j,let f(s;j;k) be T if there is a subset of 1;:;j of size at most k with correspondingsum s, and let f(s;j;k) equal F otherwise. Then the recurrence.f(s;j;k) = f(s;j 1;k) f(s aj;j 1;k 1);together with appropriate boundary conditions, allows us to determine all the valuesf(s;j;k) in O(1) steps per value.For each s = 1;:;s0let asbe the smallest size of a subset of 1;:;n withcorresponding sum s if there is such a subset, and let as= 0 if not; and let bsbe thesecond smallest size of a subset of 1;:;n with corresponding sum s if there are atleast two such subsets, and let bs= 0 if not. We have seen that we can calculate allthe values f(s;j;k) in O(n2s0) steps. From these values f(s;j;k), we can calculate allthe values asand bswithin the same time bound, as follows.C. McDiarmid/Discrete Applied Mathematics 98 (1999) 121130129To calculate as, note that as=0 if f(s;n;n)=F and if not then asis the smallest ksuch that f(s;n;k) = T. Now suppose that as6= 0, and consider how to calculate bs.Note that, if f(s;j;k) = T then we can ?nd a subset of 1;:;j of size at most kwith corresponding sum s, by backtracking through the recurrence. We can also tellif there is more than one such subset by checking if the right side in the recurrenceever has both terms T. If corresponding to f(s;n;n) (which we know is T) there isa unique solution, then bs= 0. Otherwise, bsis the least k such that corresponding tof(s;n;k) there is more than one solution.If bs=0 for each s then there can be no balanced subset. Suppose now that there isat least one non-zero value bs, and let t be a value s which minimises as+bsover alls with bs6= 0. Let Atand Btbe distinct sets each with corresponding sum t and suchthat |At| = atand |Bt| = bt. (We can ?nd such sets quickly.) The following claim willcomplete our proof.Claim. The sets Atand Btare disjoint; and Ct= At Btis a smallest balanced set.Proof of claim. Suppose that the distinct sets Atand Btmeet. Denote the sum for AtBtby u. Then this is also the sum for Bt At. But now au+ buat+ bt, contradictingour choice of t. Thus Atand Btare disjoint as claimed, and Ctis balanced.Now consider any balanced set C, with parts the disjoint sets A and B, each summingto s. Then A and B are distinct sets each summing to s. Hence |C| = |A| + |B|as+ bsat+ bt= |Ct|.5. Concluding remarksWe have seen that, even for a very restricted case of the cutting stock problem,it is strongly NP-hard to minimise the number of distinct patterns used, and thus wecannot expect to be able to solve such problems even in pseudo-polynomia
温馨提示:
1: 本站所有资源如无特殊说明，都需要本地电脑安装OFFICE2007和PDF阅读器。图纸软件为CAD,CAXA,PROE,UG,SolidWorks等.压缩文件请下载最新的WinRAR软件解压。
2: 本站的文档不包含任何第三方提供的附件图纸等，如果需要附件，请联系上传者。文件的所有权益归上传用户所有。
3.本站RAR压缩包中若带图纸，网页内容里面会有图纸预览，若没有图纸预览就没有图纸。
4. 未经权益所有人同意不得将文件中的内容挪作商业或盈利用途。
5. 人人文库网仅提供信息存储空间，仅对用户上传内容的表现方式做保护处理，对用户上传分享的文档内容本身不做任何修改或编辑，并不能对任何下载内容负责。
6. 下载文件中如有侵权或不适当内容，请与我们联系，我们立即纠正。
7. 本站不保证下载资源的准确性、安全性和完整性, 同时也不承担用户因使用这些下载资源对自己和他人造成任何形式的伤害或损失。
提示  人人文库网所有资源均是用户自行上传分享，仅供网友学习交流，未经上传用户书面授权，请勿作他用。
关于本文
本文标题：空气滤清器连接板的冲孔、冲槽、落料复合模设计【优秀】【word+12张CAD图纸全套】【冲压复合模类】【毕设】
链接地址：https://www.renrendoc.com/p-298663.html

官方联系方式

网站客服网站客服      侵权投诉侵权投诉
1:下载资料失败解决办法   
2:不支持迅雷下载,请使用浏览器下载   
3:不支持QQ浏览器下载,请用其他浏览器   
4:下载后的文档和图纸-无水印   
5:文档经过压缩，下载后原文更清晰   
点击下载此资源
关于我们 - 网站声明 - 网站地图 - 资源地图 - 友情链接 - 网站客服 - 联系我们

网站客服QQ：2881952447     

copyright@ 2020-2025  renrendoc.com 人人文库版权所有   联系电话：400-852-1180

备案号:蜀ICP备2022000484号-2       经营许可证: 川B2-20220663       公网安备川公网安备: 51019002004831号

本站为文档C2C交易模式，即用户上传的文档直接被用户下载，本站只是中间服务平台，本站所有文档下载所得的收益归上传人(含作者)所有。人人文库网仅提供信息存储空间，仅对用户上传内容的表现方式做保护处理，对上载内容本身不做任何修改或编辑。若文档所含内容侵犯了您的版权或隐私，请立即通知人人文库网，我们立即给予删除！