回转体质心位置检测设备的设计
24页 4300字数+说明书+任务书+外文翻译+4张CAD图纸【详情如下】
任务书.doc
回转体质心位置检测设备的设计论文.doc
外文翻译--应力为基础的有限元方法应用于灵活的曲柄滑块机构.doc
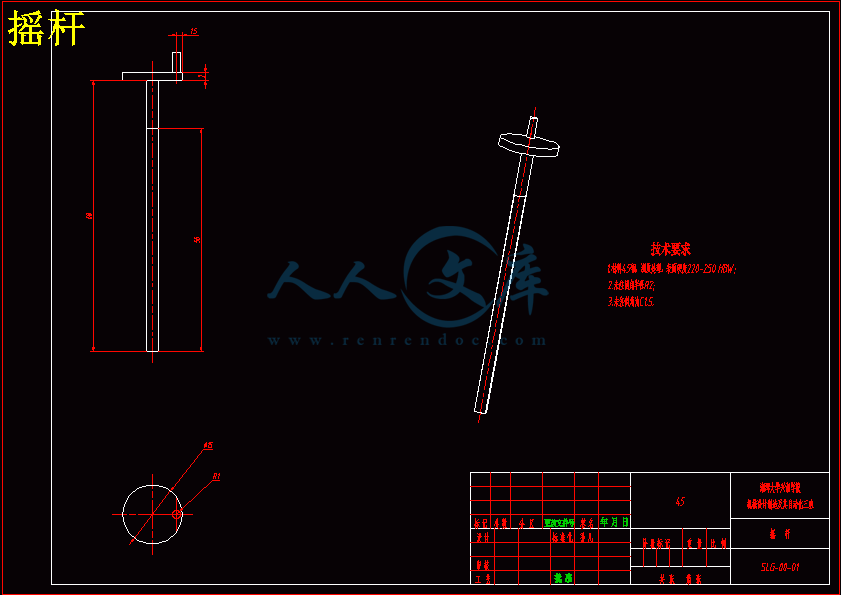
摇杆.dwg
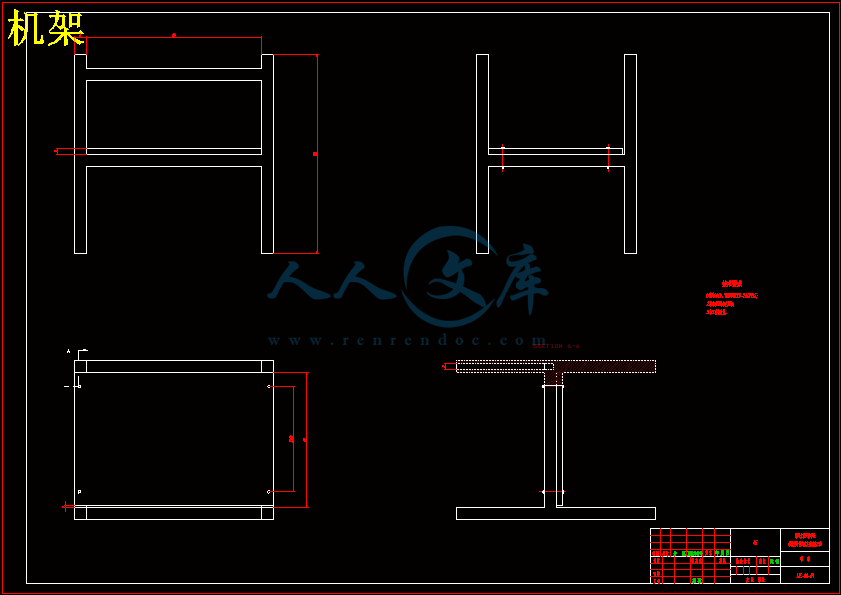
机架.dwg
脚轮.dwg
装配图.dwg


目录
·摘要2
·Abstract3
第一章 绪论4
1.1 国内外现状4
1.2 研究的目的和意义4
第二章 方案设计5
2.1方案设计一5
2.1.1质心和质量检测装置.5
2.1.2工件质心检测的基本原理5
2.2 方案设计二11
2.2.1结构组成11
2.2.2检测工件的基本原理11
2.2.3质心的三点法测量原理12
2.2.4选择-------------------13
第三章 手动升降台的设计14
3.1结构组成14
3.1.1 工作原理14
3.1.2 摇杆的设计15
3.1.3升降杆的设计16
3.1.4轴承的设计17
3.1.5上底板的设计18
3.2升降台的上升说明-19
总结感谢23
参考文献24
回转体质心位置检测设备的设计
摘要 本文主要从工程的角度上探讨了非均匀回转体工件采用四点旋转法检测质心的方法。并利用此方法初步设计了质心和质量的自动检测装置。 在装置中,采用了同步带传动机构及摩擦驱动装置,并采用了液制系统进行驱动检测参数要求的换位和摩擦轮的压力调节,保证了检测装置的正确位置和摩擦轮接触正压力的有效工作范围。
在驱动方式上,采用了直接转矩控制和速度控制两种控制模式,以应付不同参数检测的要求,使其机械系统运行更加平稳。针对每种参数的检测传感器,分别配用了相应的信号放大电路、滤波电路和检测数据处理的专用单片机系统,使各个参数的检测自成系统。各参数的单片机采用内部通信方式将各单片机系统有机结合,通过主单片机系统进行协调与调度,使系统具有进行数据处理的能力,保证了相关参数检测的同步性,从而克服了因程序流程造成的时间差异引起的检测误差,使
检测系统的适时精度得到提高。为保证各传感器检测的信号具有足够高的分辨率,采用了微伏级高精度稳压电电源和具有微处理器的24位A/D转换器ADS1211,并设计了相应的高精度信号放大器和低通滤波器。
关键词质心 滤波器 分辨率
Design of rotary centroid position detection equipment
· Abstract
This paper mainly from the point of view of project and discusses the method of non uniform revolving body workpiece with four rotating method to detect centroid. And preliminary design of the center of mass and the quality of the automatic detection device using this method.
In the device, the synchronous belt transmission mechanism and a friction drive device, and the liquid system requires the drive parameters of the transposition and friction wheel pressure regulation, ensure the effective working range of the correct position and friction wheel contact detecting device of positive pressure.
In a driving way, using the direct torque control and speed control of two kinds of control mode, to meet different detecting, the mechanical system run more smoothly. For every sensor parameters, respectively, a signal amplifying dedicated microcontroller system circuit, filter circuit and the testing data processing, a system of testing the parameters. The parameters of the single-chip microcomputer with internal communication mode combines the MCU system, coordination and scheduling by principal microcomputer system, so that the system has the ability of data processing, to ensure the synchronization parameters detection, thus overcoming the detection error caused by time difference caused by the process, so that the
To improve the precision of detection system. To ensure the signal of each sensor has high enough resolution, using the 24 bit A/D converter ADS1211 microvolt precision regulated power supply and a microprocessor, and the design of high precision signal amplifier corresponding and low pass filter.
· keyword
Centroid filter resolution
第一章 绪论
当一个回转体工件制作完场后,根据使用要求往往需要知道较精确的质心位置,用以准确计算工件的动力学特性。对于质量分布均匀的工件,比较简单,可以直接计算出来,但对于非均匀工件,特别是非均匀组装件的计算则比较困难,而且还很难保证精确度。因此需要利用相应的检测装置,将这些参数直接而准确地检测出来。
1.1国内外现状
目前国内外普遍使用的质心检测方法主要有三点测量法,四点测量法等;常用的转动惯量检测方法主要有三线摆法、能量法、转动法和扭转震动和振幅测定法等。
美国Space Electronios公司目前是航天大尺寸物体质量性能测量的领先者。所销售的转动惯量测试仪大约是世界上其他公司销量的总和。其质心测量仪是目前世界上最准确的。其成功的一个主要原因是采用了无摩擦气体轴承和平衡力矩测量技术。独特的气体轴承设计可以在一台机器上一次测量动平衡度、转动惯量、质心质量。
国内西安交通大学现代设计及转子轴承系统教育部重点实验室采用扭摆震动振幅测试法,对轴向最大负荷为10KN的转动惯量测试台磁悬浮系统的电磁阻尼进行了试验研究,结果表明该磁悬浮系统中,向心电磁轴承的电磁阻尼起决定性作用。同时还采用有限元法和级数法对电磁推力轴承和径向轴承中的电磁场进行了计算,理论计算的结果与实验测量的结果有很好的一致性,转动惯量的计算值与实验值的误差仅为1.09%。
1.2研究的目的和意义
目的是要解决长径较大的非均匀质量分布回转体工件的质心和质量的检测问题。同时提出多设备同时检测的数据通信网络的构建方法,为今后的多检测设备、多参数同时检测并进行产品的整体系统动态测试和混合仿真试验分析打下基础。
第二章 设计方案
2.1设计方案一
2.1.1质心和质量检测装置
结构组成:检测装置有检测平台、摩擦驱动轮组、支撑轮组、测力传感器和测力平台及液压系统等部分组成,(图1)。
2.1.2工件质心检测基本原理
将工件放置在检测装置中、启动质心检测功能,这时检测平台由四个对称分布的测力传感器顶起脱离平台支撑面(图二)由摩擦驱动轮组驱动被测工件做定轴转动。工件每转90度为一个质心检测位置,每个检测位置工件都停下来,摩擦轮组离开支撑轮组(见下图)。一个位置检测完毕后,摩擦轮组在油缸的驱动下置位,将工件顺着原方向再转90度,摩擦轮组重新离开支撑轮组,周而复始,直到一周的四个位置全部检测完毕。工作原理
向右摇动手轮带动连杆转动、连杆上的螺纹和推动块的螺纹相啮合,推动块向轴向固定块移动,此时上底板开始上升,当推动块接触轴向固定块时;升降工作台达到最高值;向左摇动手轮,推动块向首轮移动升降台开始下架,当推动块接触固定块时升降台达到最低点。 如上图所示手轮和连杆固定在一起叫摇杆,手轮直径145mm,厚度63mm,连杆长度620mm,直径28mm;
连杆螺纹的设计
大径 30.1625mm
小径 28.48356mm
螺距 1.41224mm
角度 60
轴尺寸 29.94152mm
方法 剪切
成型 统一标准
螺纹头数 1
长度 500mm
3.1.3升降杆的设计
升降杆有四根,上底板就是由升降杆提供的向上的力,两根连杆之间由销连接。而连杆的两头分别连接上底板和轴承。 到现在为止,论文基本已经定稿,想到开始的时候我基本不知道怎么动手,现在却可以说完成的相当理想的情况,这期间可以说是一个探索的过程,碰到了不少的新鲜东西,也用到了不少旧的事物。这次的毕业设计对我来说是一个考验,这会为我未来的工作奠定一个良好的基础。
在这次毕业设计中,软件的使用必不可少,尤其是NX。这次毕业设计使我运用软件方面有了不少的提高,为以后工作的展开有坚实的基础。其中不少东西涉及我们平时所学,为了完成毕业设计我不得不重新拾起旧的记忆,所以这次相当让我对大学知识的一次归纳,使我爱上我的专业。在这次毕业设计中我也充分认识自己的不足,实践和理论还是存在差别的,只有不断的积累经验了,才能真正做到学所有用。
这次毕业设计的题目、设计具体细则是在马秋成老师的悉心指导下完成的。老师在毕业设计的过程中付出了很多,因此,时至今日,请容许我像我的老师表示由心的感谢。?
在将来我会向这次毕业设计一样,用一样的热情和态度去加强理论和实践的结合去迎战新的挑战。
参考文献
【1】濮良贵, 纪名刚. 机械设计[M]. 北京:高等教育出版社,2006.
【2】罗圣国.吴宗泽. 机械设计课程设计手册[M]. 北京:高等教育出版社,2006.
【3】李必文.机械精度设计与检测[M]. 长沙:中南大学出版社,2011.
【4】潘存云,唐先进. 机械原理[M]. 长沙:中南大学出版社,2011.
【5】卢志辉、孙志扬、陈惠南、李祥云、费星如;旋转体质心形心和质心横偏量的测量机构设计及精度分析【J】机械设计;2010(04)
【6】曾敏、陈东;固体火箭发动机质心计算测量研究【J】计算机测量与控制;2010(09)
【7】于治会;下卧式径向偏心仪【J】宇航计测技术;1995(02)
【8】朱俊杰、陈田英、蔺美俊;正确选择和使用电子天平【J】宇航计测技术;1997(04)
【9】吴庆鸣、涂志国、杨文清、李国超;发动机质心测量方案研究【J】航空制造技术;2003(11)
【10】张可强;复杂回转体零件简易质心测量装置的设计《机械工程师》2008(12)
【11】郑宾、侯文、杨瑞峰;大尺寸柱状结构质量、质心测量方法【J】测试技术学报;2002(02)
【12】刘建营;固体火箭发动机质心测量技术述评【J】固体火箭技术;1991(04);
【13】成大先.机械设计手册:第3卷[M].第四版.北京:化学工业出版社,2002.
【14】濮良贵,纪名刚. 机械设计(第八版)[M].北京:高等教育出版社,2006.
 川公网安备: 51019002004831号
川公网安备: 51019002004831号