首页 人人文库网 > 图纸下载 > 毕业设计 > 新型卫生筷子盒总体方案与传动机构设计【优秀】【word+4张CAD图纸】【毕设】
鉴定意见.doc

新型卫生筷子盒总体方案与传动机构设计【优秀】【word+4张CAD图纸】【毕设】

收藏

压缩包内文档预览：
预览图 预览图 预览图 预览图
编号：315996    类型：共享资源    大小：1.85MB    格式：RAR    上传时间：2014-08-22 上传人：QQ14****9609 IP属地：陕西
45
积分
举报
举报 版权申诉
版权申诉 word格式文档无特别注明外均可编辑修改；预览文档经过压缩，下载后原文更清晰！ 立即下载
关 键 词：
新型 卫生筷 总体方案 传动 传动机构 卫生筷子盒
资源描述：

新型卫生筷子盒总体方案与传动机构设计【优秀】【word+4张CAD图纸】【毕设】

【带任务书+开题报告+鉴定意见+评阅表+外文翻译】【26页@正文10500字】【详情如下】【需要咨询购买全套设计请加QQ1459919609】

pdf打印图纸

任务书.doc

摇把.dxf

新型卫生筷子盒总体方案与传动机构设计.doc

新型筷子盒装配图.dxf

滑动推块.dxf

评阅表.doc

转轮.dxf

鉴定意见.doc

湘  潭  大 学

毕业论文（设计）任务书

论文（设计）题目：   新型卫生筷子盒总体方案与传动机构设计                                        

一、主要内容及基本要求

   卫生筷子盒能定期消毒清洗，满足餐饮用具卫生要求，适合于食堂、餐馆等大型用餐场合，也适合于家庭小型用餐场合。目前市场现有产品中存在诸多问题，新型卫生筷子盒要求能解决现存问题，针对产品功能进行合理化设计，实现避免大量电消耗、取筷子时筷子不直接与外界接触、一次准确出一双筷子等功能；要求结构简单，避免造价成本昂贵；各个模块方便拆解，能实现批量生产，易于推广。因此，该课题具有很好的理论意义和工程应用价值。                                                                  

   本课题的主要研究内容为：对新型卫生筷子盒进行总体方案与传动机构设计。                                                  

   总体方案设计部分主要内容为：根据产品功能要求，对机构原理进行方案设计与各部分结构初步设计。                                                          

   传动机构部分主要研究内容为：对所采用的传动机构进行结构设计与计算。                                                                      

   基本要求为：以某型卫生筷子盒为设计计算实例，提交三维原理图与产品结构总装配图，传动机构零件图，毕业论文。                                                            

二、重点研究的问题

   根据产品功能要求，对机构原理进行方案分析与选择，各部分结构初步设计，产品结构功能总装图设计，是本课题重点研究的问题。                                                

三、进度安排

序号各阶段完成的内容完成时间

1资料收集3.17

2毕业设计开题3.17~3.20

3方案确定3.22

4设计计算4.15

5毕业设计中期检查4.15~4.20

6三维建模及性能分析5.5

7完善设计、翻译及论文撰写5.25

8毕业答辩5.30~6.10

四、应收集的资料及主要参考文献

        参考文献

[1] 潘存云，唐进元.机械原理[M].长沙：中南大学出版社，2011：41-69．

[2] 濮良贵，纪名刚.机械设计[M].北京：高等教育出版社，2006：22-36.

[3] 王先逵.机械制造工艺学[M].北京：机械工业出版社，2013：230-248.

[4] 王湘江，何哲明.机械原理课程设计指导书[M].长沙：中南大学出版社，201176-82.

[5] 童秉枢，吴志军，李学志，冯涓.机械CAD技术基础[M].北京：清华大学出版社，2008：131-163.

[6] 姜勇，赵云伟，卢圣春.机械制图基础培训教程[M].北京：人民邮电出版社，2010：1-200.

[7] 娄建国.机械研究与应用[J].按最佳传动角的曲柄滑块机构的优化设计.2003：8-11.

[8] 赵又红，周知进.机械设计课程设计指导.[M].长沙：中南大学出版社，2012：24-27.

[9] 熊诗波，黄长艺.机械工程测试技术基础[M].北京：机械工业出版社，2012：99-124.

[10] 阎邦椿.机械设计手册（第5版）第2卷[M].北京：机械工业出版社，2010：35-65.

 目录

一、引言11

1.1课题背景与意义11

   1.2国内外研究现状11

1.3课题研究内容12

1.4本章小结12

二、总体方案设计13

2.1初步方案设计与选择13

一、设计方案113

  （一）储筷机构的设计13

  （二）分筷机构设计13

  （三）运输机构的设计14

二、设计方案215

  （一）储筷盒和筷槽的配合设计16

  （二）箱体（底座）和紫外线灯管槽的设计16

  （三）传动机构的设计16

2.2产品主要零部件设计16

2.3新型卫生筷子盒总体装配18

三、传动机构设计22

   3.1 传动机构比较与分析22

一、齿轮传动22

二、带传动22

三、链传动22

四、涡轮蜗杆传动23

3.2传动机构的选择与详细设计23

3.2.1 曲柄滑块传动机构设计23

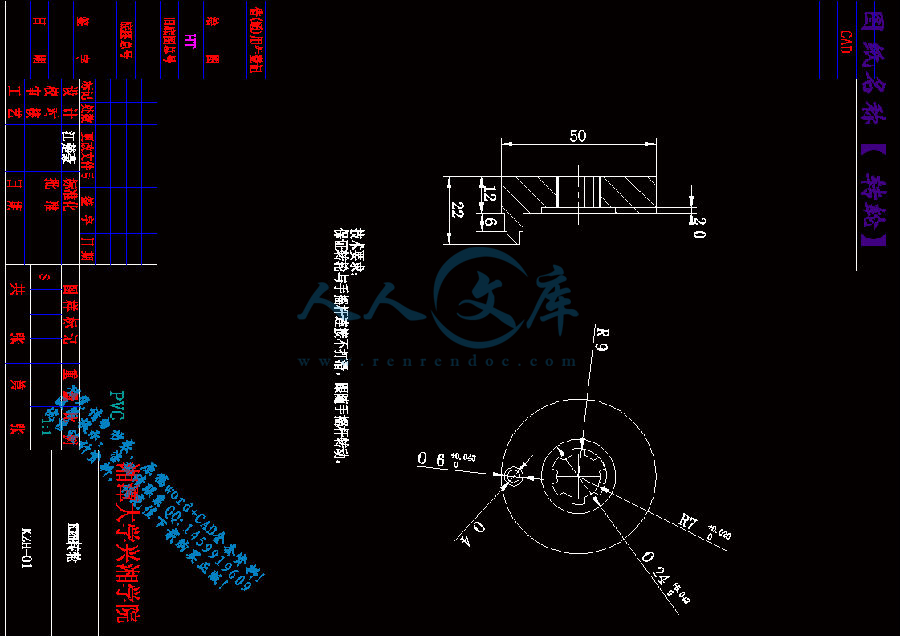
  （一）转轮的设计与尺寸24

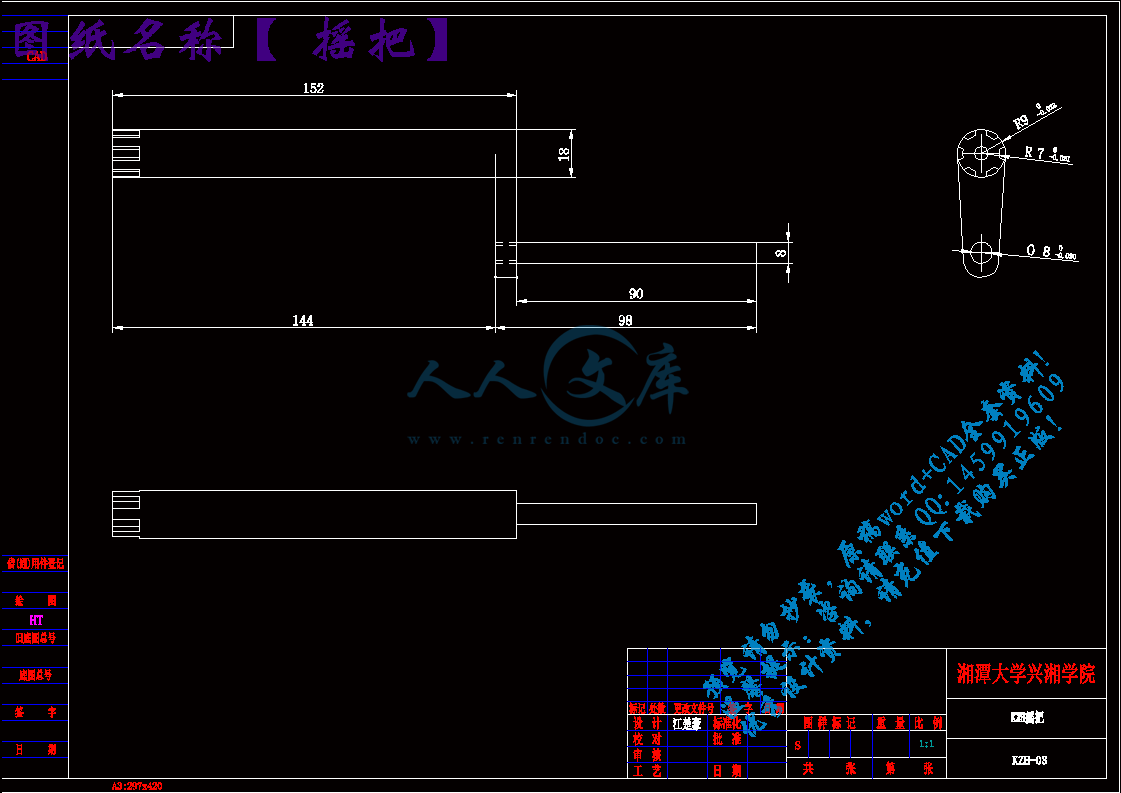
  （二）摇把的设计与尺寸25

  （三）转轮挡圈的设计与尺寸25

  （四）螺栓的设计与尺寸26

  （五）连杆的设计与尺寸27

  （六）滑块的设计与尺寸27

3.3传动机构的设计计算28

  （一）连杆长度与筷子长度的配合计算28

  （二）传动机构强度计算29

四、总结30

五、参考文献31

六、致谢32

七、英文翻译33

摘要：目前市场现有产品中存在诸多问题，新型卫生筷子盒要求能解决现存问题，针对产品功能进行合理化设计，要求结构简单，避免造价成本昂贵；各个模块方便拆解，能实现批量生产，易于推广。因此，该课题具有很好的理论意义和工程应用价值。

该论文介绍了新型卫生筷子盒的设计。论文中的新型卫生筷子盒能够通过曲柄滑块机构做为传动机构，一次准确出一双筷子，并能够通过紫外线灯管进行对筷子的消毒。在该新型筷子盒的设计中，传动机构的设计是难点之一，起初选择的传动机构是带传动，但此传动机构会很占筷子盒体积，且使筷子盒功能的实现变得更加复杂，因此，通过比较选用曲柄滑块作为传动机构。此种新型卫生筷子盒设计结构简单，造价成本较低，各个模块方便拆解，是一种健康，方便，卫生的新型筷子盒。

关键词 ：卫生筷子盒；曲柄滑块；紫外线灯

The overall program design and transmission of the new health chopsticks box

Abstract: At present ,the existing products currently on the market have many problems, the new health chopsticks box required to solve the existing problems, to rationalize the design features for the product, requiring a simple structure to avoid the cost of expensive; each module easy to disassemble, to achieve mass production, easy to spread. Thus, the subject has a good theoretical and engineering application.

   A new health chopsticks box design is introduced in this thesis.  A new health chopsticks box can be used as the transmission mechanism through slider-crank mechanism, once a pair of chopsticks and accurate, and can be sterilized chopsticks by UV lamp. In the novel design chopstick case, the design of the drive mechanism is one of the difficulties, the drive mechanism is initially selected tape drive, but the drive mechanism will be the volume of the cartridge representing chopsticks and chopstick case so achieve more complex functionality, Thus, by comparing the selection of a slider-crank drive mechanism. Such a simple box design structure new health chopsticks have low cost, and it is easy to disassemble each module.So it is a healthy, convenient, new chopsticks box hygiene.

Keywords: Health chopsticks box; crank slider; ultraviolet light

  第一章  引言

1.1 课题背景与意义

卫生筷子盒能定期消毒清洗，满足餐饮用具卫生要求，适合于食堂、餐馆等大型用餐场合，也使用与家庭小型用餐场合。目前市场现有产品存在诸多问题，新型卫生筷子盒要求能解决现存问题，针对产品功能进行合理化设计，实现避免大量电消耗、取筷子时筷子不直接与外界接触、一次准确出一双筷子等功能；要求结构简单，避免造价成本昂贵；各个模块方便拆解，能实现批量生产，易于推广。因此，该课题具有很好的理论意义和工程应用价值。

现实生活中，大部分中国家庭吃饭时都是用筷子的，而筷子卫生存在很大的健康隐患，如果长期使用不卫生的筷子，就容易染上消化道疾病，如肝炎、痢疾、急性胃肠炎等。而现在人们日常生活中常用的筷子盒中，大多数是塑料制品，结构简单、功能单一，显得既不环保又不卫生。

1.2 国内外研究现状

罗格率先引进来自德国的Nicoler空间消毒技术[6]，开创性的将空间消毒的概念引入餐具消毒领域。由于整个过程一直处于持续、不间断的灭菌状态，不仅能够彻底杀灭餐具上的乙肝病菌(芽胞)、金黄色葡萄球菌及大肠杆菌等细菌，经处理后的洁净空气能快速的循环流动，从而达到对餐具所处的整个环境持续净化。

在传动设备方面，曲柄滑块作为机械设备中一种常见的传动机构，它由于具有结构简单，运动规律明确，可以实现旋转运动和直线运动之间的变换，并且具有急回运动等优点，使其在机械工程设备中得到广泛的应用。

目前，国内外对曲柄滑块机构的优化设计及运动仿真研究有关课题的研究也不少。其中，娄建国[8]，采用几何解析方法设计偏置曲柄滑块机构，在满足给定的滑块行程和行程速比系数的前提下，借助计算机进行寻优设计，从而方便地求得具有最佳传动角的曲柄滑块机构。刘菊蓉、王旭飞[9]，运用MATLAB及其中的SIMULINK模块，对给出行程H，行程速比系数K和许用角[γ]进行设计分析。设计结果不但满足现代机械设计的要求，设计过程编程简单，而且得到曲柄在任意位置对应的其它参数。陈杰平，姚智华[11]，借助于功能强大的分析仿真软件，实现了机构性能分析和动态仿真，降低分析的难度，有效提高设计的工作效率、产品开发质量，降低开发成本。

该新型卫生筷子盒的传动机构的选择是通过选用各种传动机构来进行比较，最终选定的的曲柄滑块机构，该传动机构具有机型小，运行平稳，可靠性高等特点，是新型卫生筷子盒体积更小，取筷更方便。

1.3 课题研究内容

   本课题的主要研究内容为：对新型卫生筷子盒进行总体方案与传动机构设计。                                                  

总体方案设计部分主要内容为：根据产品功能要求，对机构原理进行方案设计与各部分结构初步设计。                                                          

传动机构部分主要研究内容为：对所采用的传动机构进行结构设计与强度计算。

1.4 本章小结

   卫生筷子盒能定期消毒清洗，满足餐饮用具卫生要求，适合于食堂、餐馆等大型用餐场合，也适合于家庭小型用餐场合。目前市场现有产品中存在诸多问题，新型卫生筷子盒要求能解决现存问题，针对产品功能进行合理化设计，实现避免大量电消耗、取筷子时筷子不直接与外界接触、一次准确出一双筷子等功能；要求结构简单，避免造价成本昂贵；各个模块方便拆解，能实现批量生产，易于推广。因此，该课题具有很好的理论意义和工程应用价值。

    参考文献

[1] 潘存云，唐进元.机械原理[M].长沙：中南大学出版社，2011：41-69．

[2] 濮良贵，纪名刚.机械设计[M].北京：高等教育出版社，2006：22-36.

[3] 王先逵.机械制造工艺学[M].北京：机械工业出版社，2013：230-248.

[4] 王湘江，何哲明.机械原理课程设计指导书[M].长沙：中南大学出版社，201176-82.

[5] 童秉枢，吴志军，李学志，冯涓.机械CAD技术基础[M].北京：清华大学出版社，2008：131-163.

[6] 姜勇，赵云伟，卢圣春.机械制图基础培训教程[M].北京：人民邮电出版社，2010：1-200.

[7] 娄建国.机械研究与应用[J].按最佳传动角的曲柄滑块机构的优化设计.2003：8-11.

[8] 刘菊蓉，王旭飞.机械研究与应用[J].偏置式曲柄滑块机构的优化设计及运动分析.2005：10-14.

[9] 赵又红，周知进.机械设计课程设计指导.[M].长沙：中南大学出版社，2012：24-27.

[10] 陈杰平，姚智华.中文科技期刊数据库[J].基于MATLAB的曲柄滑块机构仿真研究.2005：31-34.

[11] 熊诗波，黄长艺.机械工程测试技术基础[M].北京：机械工业出版社，2012：99-124.

[12] 阎邦椿.机械设计手册（第5版）第2卷[M].北京：机械工业出版社，2010：35-65.


内容简介：
CAD旧底图总号A3:297x420签 字日 期绘 图借(通)用件登记底图总号HT标记设 计共 张S图 样 标 记重 量 比 例湘湘湘湘湘湘湘湘处数更改文件号签 字日 期标准化校 对审 核工 艺日 期批 准第 张1:1江楚豪KZH摇把KZH-039890815214418R 70-0.021O80-0.020R 90-0.023H7h6技术要求：1.完成装配后，尝试转动手柄时应平顺，轻松带动滑块完成运动。2.调整筷子盒盒体内调节板，平齐将要放置的筷子。标记设 计共 张S图 样 标 记重 量比 例湘潭大学兴湘学院处数更改文件号签 字日 期标标标校 对审 核工 艺日 期批 标第 张KZH总装配4513后后1 PVC .253 kg12六角头螺栓M3.5x13Hex head metric machine screw ANSI B18.6.7M M3.5x131钢 .001 kg11六角头螺栓M6x10Hex head metric machine screw ANSI B18.6.7M M6x105钢 .005 kg10摇摇100mm1 PVC .003 kg9手摇摇1 PVC .082 kg8转转1 PVC .029 kg7挡挡1 PVC .001 kg6紫紫紫紫3 (None)5滑动滑块1 PVC .006 kg4底底1 PVC2.613 kg2.613筷子盒后1 PVC .826 kg2筷子盒调节挡板1 Polycarbonate .454 kg1筷子盒1 Polycarbonate5.423 kg5.42序号文件文文名数量材材单重总重备备质量121011718320603604601001:2.5江楚豪KZH-04旧底图总号签 字日 期绘 图借(通)用件登记底图总号HTCAD标记设 计共 张S图 样 标 记重 量 比 例湘湘湘湘湘湘湘湘处数更改文件号签 字日 期标准化校 对审 核工 艺日 期批 准第 张PVC2:1KZH滑块KZH-0212.115524208.77R 6江楚豪Ra2.3Ra2.3260-0.045O2.85旧底图总号签 字日 期绘 图借(通)用件登记底图总号HTCAD标记设 计共 张S图 样 标 记重 量 比 例湘湘湘湘湘湘湘湘处数更改文件号签 字日 期标准化校 对审 核工 艺日 期批 准第 张PVC1:1江楚豪KZH-01技术要求：保证转轮与手摇杆连接不打滑，跟随手摇杆转动。R 9O45022126KZH转轮R 7+0.0200O6+0.0430O24+0.04302 0湘 潭 大 学毕业论文（设计）任务书论文（设计）题目： 新型卫生筷子盒总体方案与传动机构设计 学号： 2010963013 姓名： 江楚豪 专业： 机械设计制造及其自动化 指导教师： 唐新姿 系主任： 刘柏希 一、主要内容及基本要求 卫生筷子盒能定期消毒清洗，满足餐饮用具卫生要求，适合于食堂、餐馆等大型用餐场合，也适合于家庭小型用餐场合。目前市场现有产品中存在诸多问题，新型卫生筷子盒要求能解决现存问题，针对产品功能进行合理化设计，实现避免大量电消耗、取筷子时筷子不直接与外界接触、一次准确出一双筷子等功能；要求结构简单，避免造价成本昂贵；各个模块方便拆解，能实现批量生产，易于推广。因此，该课题具有很好的理论意义和工程应用价值。 本课题的主要研究内容为：对新型卫生筷子盒进行总体方案与传动机构设计。 总体方案设计部分主要内容为：根据产品功能要求，对机构原理进行方案设计与各部分结构初步设计。 传动机构部分主要研究内容为：对所采用的传动机构进行结构设计与计算。 基本要求为：以某型卫生筷子盒为设计计算实例，提交三维原理图与产品结构总装配图，传动机构零件图，毕业论文。 二、重点研究的问题 根据产品功能要求，对机构原理进行方案分析与选择，各部分结构初步设计，产品结构功能总装图设计，是本课题重点研究的问题。 三、进度安排序号各阶段完成的内容完成时间1资料收集3.172毕业设计开题3.173.203方案确定3.224设计计算4.155毕业设计中期检查4.154.206三维建模及性能分析5.57完善设计、翻译及论文撰写5.258毕业答辩5.306.10四、应收集的资料及主要参考文献 参考文献1 潘存云，唐进元.机械原理M.长沙：中南大学出版社，2011：41-692 濮良贵，纪名刚.机械设计M.北京：高等教育出版社，2006：22-36.3 王先逵.机械制造工艺学M.北京：机械工业出版社，2013：230-248.4 王湘江，何哲明.机械原理课程设计指导书M.长沙：中南大学出版社，201176-82.5 童秉枢，吴志军，李学志，冯涓.机械CAD技术基础M.北京：清华大学出版社，2008：131-163.6 姜勇，赵云伟，卢圣春.机械制图基础培训教程M.北京：人民邮电出版社，2010：1-200.7 娄建国.机械研究与应用J.按最佳传动角的曲柄滑块机构的优化设计.2003：8-11.8 赵又红，周知进.机械设计课程设计指导.M.长沙：中南大学出版社，2012：24-27.9 熊诗波，黄长艺.机械工程测试技术基础M.北京：机械工业出版社，2012：99-124.10 阎邦椿.机械设计手册（第5版）第2卷M.北京：机械工业出版社，2010：35-65. 英文原稿Application of Stress-based Finite Element Method to a Flexible Slider Crank Mechanism（Y.L.Kuo University of Toronto W.L.Cleghorn University of Canada）AbstractThis paper presents a new procedure to apply the stress-based finite element method on Euler-Bernoulli beams.An approximated bending stress distribution is selected,and then the approximated transverse displacement is determined by integration.The proposed approach is applied to solve a flexible slider crank mechanism.The formulation is based on the Euler-Lagrange equation,for which the Lagrangian includes the components related to the kinetic energy,the strain energy,and the work done by axial loads in a link that undergoes elastic transverse deflection.A beam element is modeled based on a translating and rotating motion.The results demonstrate the error comparison obtained from the stress-and displacement-based finite element methods.Keywords:stress-based finite element method;slidercrank mechanism;Euler-Lagrange equation.1.IntroductionThe displacement-based finite element method employs complementary energy by imposing assumed displacements.This method may yield the discontinuities of stress fields on the inter-element boundary while employing low-order elements,and the boundary conditions associated with stress could not be satisfied.Hence,an alternative approach was developed and called the stress-based finite element method,which utilizes assumed stress functions.Veubeke and Zienkiewicz1,2were the first researchers introducing the stress-based finite element method.After that,the method was applied to a wide range of problems and its applications3-5In addition,there are various books providing details about the method6,7.The operation of high-speed mechanisms introduces vibration,acoustic radiation,wearing of joints,and inaccurate positioning due to deflections of elastic links.Thus,it is necessary to perform an analysis of flexible elasto-dynamics of this class of problems rather than the analysis of rigid body dynamics.Flexible mechanisms are continuous dynamic systems with an infinite number of degrees of freedom,and their governing equations of motion are modeled bynonlinear partial differential equations,but their analytical solutions are impossible to obtain.Cleghorn et al.8-10included the effect of axial loads on transverse vibrations of a flexible four-bar mechanism.Also,they constructed a translating and rotating beam element with a quintic polynomial,which can effectively predict the transverse vibration and the bending stress.This paper presents a new approach for the implementation of the stress-based finite element method on the Euler-Bernoulli beams.The developed approach first selects an assumed stress function.Then,the approximated transverse displacement function is obtained by integrating the assumed stress function.Thus,this approach can satisfy the stress boundary conditions without imposing a constraint.We apply this approach to solve a flexible slider crank mechanism.In order to show the accuracy enhancement by this approach,the mechanism is also solved by the displace-based finite element method.The results demonstrate the error comparison.II.Stress-based Method for Euler-Bernoulli BeamsThe bending stress of Euler-Bernoulli beams is associated with the second derivative of the transverse displacement,namely curvature,which can be approximated as the product of shape functions and nodal variables:Where is a row vector of shape functions for the ith element; is a column vector of nodal curvatures,y is the lateral position with respect to the neutral line of the beam,E is the Youngs modulus,and is the transverse displacement,which is a function of axial position x.Integrating Eq.(1)leads to the expressions of the rotation and the transverse displacement as Rotation： Transverse displacement: Where and are two integration constants for the ith element,which can be determined by satisfying the compatibility.Substituting Eqs.(2)and(3)into(1),the finite element displacement,rotation and curvature can beexpressed as: where the subscripts(C),(R)and(D)refer to curvature,rotation and displacement,respectively.By applying the variational principle,the element and global equations can be obtained11-13.Table 1:Comparison of the displacement-and the stress-based finite element methods for anEuler-Bernoulli beam elementIII.Comparisons of the Displacement-and Stress-based Finite Element MethodsThe major disadvantage of the displacement-based finite element method is that the stress fields at the inter-element nodes are discontinuous while employing low-degree shape functions.This discontinuity yields one of the major concerns behind the discretization errors.In addition,it might use excessive nodal variables while formulating stiffness matrices.The stress-based method has several advantages over the displacement-based finite method.First of all,the stress-based method produces fewer nodal variables (Table 1).Secondly,when employing the stress-basedfinite method,the boundary conditions of bending stress can be satisfied,and the stress is continuous at theinter-element nodes.Finally,the stress is calculated directly from the solution of the global system equations.However,the only disadvantage of the stress-based finite method is that the integration constants are different for each element.IV.Generation of Governing EquationThe slider crank mechanism shown in Fig.1 is operated with a prescribed rigid body motion of the crank,and the governing equations are derived using a finite element formulation.The derivation procedure of the finite element equations involves:(1)deriving the kinematics of a rigid body slider crank mechanism;(2) constructing a translating and rotating beam element based on the rigid body motion of the mechanism;(3)defining a set of global variables to describe the motion of a flexible slider crank mechanism;(4)assembling all beam elements.Finally,the global finite element equations can be obtained,and the time response of a flexible slider crank mechanism can be obtained by time integration.A.Element equation of a translating and rotating beamConsider a flexible beam element subjected to prescribed rigid body translations and rotations.Superimposed on the rigid body trajectory,a finite number of deflection variables in the longitudinal and transverse directions is allowed.The Euler-Lagrange equation is used to derive the governing differential equations for an arbitrarily translating and rotating flexible member.Since elastic deflections are considered small,and there is a finite number of degrees of freedom,the governing equations are linear and are conveniently written in matrix form.The derivation of the element equations has been precisely presented in 8-10,and this section provides a brief summary.In view of high axial stiffness of a beam,it is reasonable to consider the beam as being rigid in its longitudinal direction.Hence,the longitudinal deflection is given as where u1 is a nodal variable,which is constant with respect to the x direction shown in Fig.2.The transverse deflection can be represented asThe velocity of an arbitrary point on the beam element with a translating and rotating motion is given aswhere is the absolute velocity of point O of the beam element shown in Fig.2;?is the angular velocity of the beam element; are the longitudinal and transverse displacements of an arbitrary point on the beam element,respectively;x is a longitudinal position on the beam element shown in Fig.2.If we letbe the mass per unit volume of element material;A,the element cross-sectional area,and L the element length,then the kinetic energy of an element is expressed asThe flexural strain energy of uniform axially rigid element with the Youngs modulus,E,and second moment of area,I,is given asThe work done by a tensile longitudinal load,(i)P,in an element that undergoes an elastic transverse deflection is given by14Longitudinal loads in a moving mechanism element are not constant,and depend both on the position in the element and on time.With the longitudinal elastic motions neglected,the longitudinal loads may be derived from the rigid body inertia forces,and can be expressed aswhere PR is an external longitudinal load acting at theright hand end of an element,andox(i )ais the absolute eacceleration of the point O in the x direction shown in Fig.2.The Lagrangian takes the formSubstituting Eqs.(5-10)into(12),and employing the Euler-Lagrange equations,the governing equations of motion for a rotating and translating elastic beam can be expressed in the following matrix form:whereMe,CeandKeare mass,equivalent damping,and equivalent stiffness matrices of a element,respectively;Feis a load vector of an element.When formulating the mass matrix of the coupler,the mass of the slider should be taken into account.B.Global equations of slider crank mechanism For the proposed approach to solve a flexible slider crank mechanism,the global variables are the curvatures on the nodes.For assembling all elements,it is necessary to consider the boundary conditions applied to the mechanism.Since a prescribed motion applied to the base of the crank,there is a bending moment at point O shown in Fig.1,i.e.,the curvature at point O exists.For points A and B shown in Fig.1,we presume that both points refer to pin joints.Thus,the bendingmoments and the curvatures at both points are zeros.Since Eq.(13)is a matrix-form expression in terms of the vector of global variables,the global equations can be obtained by directly summing up all of element equations,which can be expressed aswhereM,C,Kare global mass,damping and stiffness matrices,respectively;Fis a global load vector.V.Numerical simulation based on steady stateThe rotating speed of the crank is operating at 150rad/s(1432 rpm),and the system parameters of a flexible slider crank are as follows:R2=0.15(m),R3=0.30(m),A=0.225(kg/m),EI=12.72(N-m2),mB=0.03375(kg)where R2 and R3 are the lengths of the crank and coupler,respectively;mB is the mass of the slider.The analytical results of this paper are presented by plotting steady state transverse displacements and bending strains of midpoints on crank and coupler throughout a cycle of motion.The steady state can be obtained by adding a physical damping matrix,namely Rayleigh damping whereandare two constants,which can be determined from two given damping ratio that correspond to two unequal frequencies of vibration15. In this paper,the values ofandare determined based on the first two natural frequencies.By adding physical damping to the equations of motion,the analytical solution is obtained by performing the constant time-step Newmark method over twenty cycles of motion.The initial conditions are set to zeros when performing numerical time integration.The error indicator is defined as where QFE and QRef are two quantities based on a finite element solution and a reference solution,respectively.Generally,they are functions of time,and they can be arbitrarily selected,such as energy,displacement,bending strain,etc.t1 and t2 refer to the interval of timeintegration,which are usually one cycle after steady-state condition has been reached.Since an exact solution is not available,a reference solution is obtained by the displacement-based finite element method based on twenty elements per link with quintic polynomials in this paper.Fig.3.Time responses of the total energy,mensionless midpoint deflection of the coupler,andhe midpoint strain of the coupler at the steady state conditionVI.Numerical SimulationsIn the section,we consider the mechanism with a rigid crank.The coupler is the only flexible link.Based on the beam element constructed in Section IV.,the beam element has a rigid axial motion,but it has a transverse deflection.When we implement the stress-based finite elementmethod proposed in Section III.,it is necessary to consider the boundary conditions of the modeled links and the approximated degree of shape functions.In this example,we select a linear function along the axial axis to approximate the strain distribution of the coupler,and the boundary conditions of the coupler are considered without zero bending moment.Thus,it is impossible to model the coupler with one element.In the example,we consider the coupler discretized as two,three,four,and five elements,and its curvature distribution is approximated by a linear function asAnd then,the time responses and the errors of the total energy,the midpoint deflection of the coupler,the midpoint strain of the coupler is obtained by the stress-based finite element method.Also,the first natural frequency is evaluated.The rotating speed of the crank is operating at 150rad/s(1432 rpm),and the system parameters of a flexible slider-crank are as follow16:R2=0.15(m),R3=0.30(m),A=0.225(kg/m),EI=12.72(N-m 2),mB=0.03375(kg)where R2 and R3 are the lengths of the crank and coupler,respectively;mB is the mass of the slider.In order to compare the errors obtained by the displacement-based finite element method,we also use it to solve the mechanism,and its results are based on Ref.17.Table 2.Errors of the first natural frequency by both finite element methodsFig.3.shows the time responses of the total energy,the dimensionless midpoint deflection of coupler,and the midpoint strain of the coupler on the steady state condition.Tables 2 to 5 show the error comparisons of the first natural frequency,the total energy,the midpoint deflection of the coupler,and the midpoint strain of the coupler by the stress-and the displacement-based finite element methods.The error calculation is based on Eq. (16).The results show that the errors from the stress-based finite element method are greater than the errors from the displacement-based finite element method,when we consider the same number of elements for both methods.However,when the number of degrees of freedom is the same,the errors from thestress-based finite element method is much smaller than the errors from the displacement-based finite element method.Also,we notice that except for the errors of the first natural frequency,the errors from the stress-based finite element method are smaller than the errors from the displacement-based finite element method under the same number of elements.It illustrates that the stress-based finite element method can provide much accurate approximated solutions for kineto-elasto-dynamic problems.VII.ConclusionsThis paper proposed a new approach to implement the stress-based finite element method to Euler-Bernoulli beam problems.Especially,this approach can be applied to kineto-elasto-dynamic problems.The proposed approach is to approximate the curvature of a beam. Then,we can obtain the transverse deflection and the stress distribution by integrating the approximate curvature distribution.During the integration procedure, it is necessary to make the boundary conditions of a beam element satisfied,which can derive the integration constant.In this paper,we apply the proposed approach to solve a flexible slider crank mechanism operating a high-speed motion.The results illustrate that the errors from the stress-based finite element method are much smaller than the errors from the conventional approach, the displacement-based finite element method,when we compare the errors under the same degrees of freedom. Also,some errors show that the stress-based finite element method can provide more accurate solutions under the same number of elements.References1B.Fraeijs de Veubeke,“Displacement and equilibrium models in the finite element method”,Stress Analysis,edited by O.C.Zienkiewicz,Wiley,New York,1965.2B.Fraeijs de Veubekd and O.C.Zienkiewicz,“Strain-energy bounds in finite-element analysis by slab analogy”,J.Strain Analysis,Vol.2,pp.265-271,1967.3Z.Wieckowski,S.K.Youn,and B.S.Moon,“Stressed-based finite element analysis of plane plasticity problems”,Int.J.Numer.Meth.Engng.,Vol.44,pp.1505-1525,1999.4 H.Chanda and K.K.Tamma,“Developments encompassing stress based finite element formulations for materially nonlinear static dynamic problems”,Comp.Struct.,Vol.59,No.3,pp.583-592,1996.5M.Kaminski,“Stochastic second-order perturbation approach to the stress-based finite element method”,Int.J.Solids and Struct.,Vol.38,No.21,pp.3831-3852,2001.6O.C.Zienkiewicz and R.L.Taylor,The Finite Element Method,McGraw-Hill,London,2000.7R.H.Gallagher,Finite Element Fundamentals,Prentice-Hall,Englewood Cliffs,1975.8W.L.Cleghorn,1980,Analysis and design of high-speedflexible mechanism,Ph.D.Thesis,University of Toronto.9W.L.Cleghorn,R.G.Fenton,and B.Tabarrok,1981,“Finite element analysis of high-speed flexible mechanisms”,Mechanism and Machine Theory,16(4),407-424.10W.L.Cleghorn,R.G.Fenton,and B.Tabarrok,1984,“Steady-state vibrational response of high-speed flexible mechanisms”,Mechanism and Machine Theory,19(4/5)11Y.L.Kuo,W.L.Cleghorn and K.Behdinan,“Stress-based Finite Element Method for Euler-Bernoulli Beams”,Transactions of the Canadian Society for Mechanical Engineering,Vol.30(1),pp.1-6,2006.12Y.L.Kuo,W.L.Cleghorn,and K.Behdinan“Applications of Stress-based Finite Element Method on Euler-Bernoulli Beams”,Proceedings of the 20th Canadian Congress ofApplied Mechanics,Montreal,Quebec,Canada,May 30-Jun2,2005.13Y.L.Kuo,Applications of the h-,p-,and r-refinements of the Finite Element Method on Elasto-dynamic Problems,Ph.D.Thesis,University of Toronto,2005.14L.Meirovitch,1967,Analytical Methods in VibrationsMacmillan,New York,436-463.15K.J.Bathe,1996,Finite Element Procedures,Prentice Hall Englewood Cliffs,NJ,USA.16A.L.Schwab and J.P.Meijaard,2002,“Small vibrations superimposed on prescribed rigid body motion”,Multibody System Dynamics,8,29-49.17Y.L.Kuo and W.L.Cleghorn,“The h-p-r-refinement FiniteElement Analysis of a High-speed Flexible Slider Crank Mechanism”,Journal of Sound and Vibration,in press. 英文翻译应力为基础的有限元方法应用于灵活的曲柄滑块机构（多伦多大学：Y.L. Kuo .L. Cleghorn加拿大）摘要:本文在欧拉一伯努利梁基础上提出了一种新的适用于以应力为基础的有限元方法的程序。先选择一个近似弯曲应力的分布，然后通过一体化确定近似横位移。该方法适用于解决灵活滑块曲柄机构问题，制定的依据是欧拉-拉格朗日方程，而拉格朗日包括与动能，应变能有关的组件，并通过弹性横向挠度构成的轴向负荷的链接来工作。梁元模型以翻转运动为基础，结果表明以应力和位移为基础的有限元方法。关键词：应力为基础的有限元方法，曲柄滑块机构，拉格-朗日方程1.前言以位移为基础的有限元方法通过实行假定位移补充能量。这种方法可能由内部因素产生不连续应力场，同时由于采用了低阶元素，边界条件与压力不能得到满足。因此，另一种被成为以应力为基础采用假定应力的有限元方法得到了应用和发展。Veubeke和Zienkiewicz1-2首先对应力有限元素进行了研究。之后，这种方法被广泛用于解决应用程序中的问题3-5。此外，还有各种书籍提供更加详细的方法6.7。这一高速运作机制采用振动，声辐射，协同联结，和挠度弹性链接的准确定位。因此，有必要分析灵活的弹塑性动力学这一类的问题，而不是分析刚体动力学。 灵活的机制是一个由无限多个自由度组成的连续动力学系统，其运动方程是由非线性偏微分方程建立的模型，但得不到分析解决方案。Cleghorn et al8-10 阐述了横向振动上的轴向荷载对灵活四杆机构的影响。并且通过能有效预测横向振动和弯曲应力的五次多项式建立了一个翻转梁单元。本文提出了一种新的方法来执行建立在欧拉一伯努利基础上的以应力为基础的有限元方法。改进后的方法首先选定了假定应力函数。然后通过整合假定应力函数得到横向位移函数。当然，这种方法能解决没有强制制约因素的应力集中问题。我们可以通过这种方法解决灵活曲柄滑块机构体系中存在的问题。目的是通过这种方法提高准确性，该系统存在的问题也可以通过取代基有限元方法来解决。结果可以证明偏差比较。2.以应力为基础的欧拉一伯努利梁欧拉一伯努利梁的弯曲应力与横向位移的二阶导数相关，也就是曲率，可以近似的看做是形函数和交点变量：这里(i)N(c)是连续载体的形函数；(i)e 是列向量的交点函数，y是关于中性线的横向定位，E是杨氏模量，（i）v是横向位移，x轴向定位函数。由方程（1）可以推导出横向位移转换方程： 横向位移：这里 (i)C1和(i)C2是两个一体化常数，可以通过满足兼容性来确定。将方程（2）和（3）代入（1），可以得到有限元位移和回转曲率，如下所示：这里下标（C），（R）和（D）分别代表曲率，自转和位移。运用变分原理，可以得到这些方程11-13。表1 分别比较以位移和应力为基础的有限元方法的欧拉-伯努利梁元素以位移为基础的有限元方法以应力为基础的有限元方法近似横向位移自由度立方米立方米近似弯曲应力线性线性交点变量两端位移和回转两端曲率边界应力满足条件位移，回转位移，回转，弯曲应力自由度数量四二3.以位移和应力为基础的有限元方法的比较 主要区别在于以位移为基础的有限元方法的应力场存在不连续的内部因素，同时具有低阶形函数。主要是因为不连续量的产生以及间离散分布。再者，它可能由于使用过多交点变量而产生刚度矩阵。以应力为基础的方法与以位移为基础的方法比较具有很多优点。首先，以应力为基础的方法产生的交点变量较少（如表1）。第二，使用以应力为基础的方法时，弯曲应力的边界条件可以得到满足。最后，应力由体系方程直接计算得到。4.方程推导曲柄滑块机构如图1所示，由做刚体运动的曲柄来运作，该方程由有限元公式推导而得。有限元方程的推导过程如下：（1）建立刚体运动学曲柄滑块机构；（2）构建基于刚体运动学机构的翻转梁单元；（3）确定一套变量用来描述灵活曲柄滑块机构的运动；（4）装配所有梁单元。最后，就可以得到有限元方程，同时该灵活曲柄滑块机构的时间响应可以通过时间一体化确定。图1 灵活曲柄滑块机构A翻转梁的元方程考虑灵活的梁单元受到刚体翻转和回转运动。叠加在刚体运动轨迹时，纵向和横向方向上允许一些挠度变量。通过拉格-朗日方程可以得到任意灵活翻转的组件的微分方程。由于弹性变形认为是很小的，而且自由度是有限的，这个方程是线性的并且很容易画出来。推导公式的元素也被很明确的列出来8-10，并且做了简要的介绍。鉴于在轴向有很强的刚度，因此很有必要在纵向方向上合理考虑为刚性梁。所以，纵向方向如一下所示： （5）这里u1是交点变量，是关于x轴方向的常数，如图2所示。横向可以表示为： 翻转梁单元上任意点的速度可以表示如下：这里（i）Vax（i）Vay）是梁单元在O点的绝对速度，如图2所示； 是梁单元的角速度；（i）u（i）v）分别是梁单元上任意点纵向和横向的位移，x是梁单元纵向的定位，如图2所示。图2 旋转梁如果我们把 当作组件材料的单位体积；A是组件的横截面积，L是组件的长度，组件的动能可以表示如下： 均匀刚性组件的轴向弯曲应变能量与杨氏模量E有关，得到二阶矩阵I，如下所示：由纵向拉伸负荷工作，（i）P,组件的横向挠度表示如下： 运功机制的纵向负荷不是一成不变的，与位置和时间有关。在忽略纵向弹性形变的前提下，纵向负荷可能来自于刚性惯性力，可以表示如下：这里PR是元件右侧的外部纵向负载， 是x轴方向上O点的绝对加速度。如图2所示。 拉格-朗日形式表示如下：将公式（5-100）代入（12），并且运用欧拉-拉格朗日方程，旋转梁的运动方程可以表示为一下形式： 这里Me、Ce和Ke分别是元件的质量、等效阻尼和等效刚度矩阵；Fe是元件的载荷向量。当建立质量耦合矩阵时，应主要考虑滑块机构。B.曲柄滑块机构方程提出解决曲柄滑块机构问题的方法，变量是曲率的节点。装配所有元件时，考虑机构的边界条件是很有必要的。因为该动力适用于基础曲柄结构，在O点存在弯矩，如图1所示，在O点也存在曲率。如图1所示的A点和B点，我们假定它们是很小的点。然而，实际上，弯矩和曲率在这两个点上都为零。因为公式（13）是变量的矩阵表示方式 ，这个公式可以通过总结所有的方程来得到，可以表示如下：这里M、C、K分别是质量、阻尼和刚度矩阵，F是负载向量。5.稳定状态基础上的
温馨提示:
1: 本站所有资源如无特殊说明，都需要本地电脑安装OFFICE2007和PDF阅读器。图纸软件为CAD,CAXA,PROE,UG,SolidWorks等.压缩文件请下载最新的WinRAR软件解压。
2: 本站的文档不包含任何第三方提供的附件图纸等，如果需要附件，请联系上传者。文件的所有权益归上传用户所有。
3.本站RAR压缩包中若带图纸，网页内容里面会有图纸预览，若没有图纸预览就没有图纸。
4. 未经权益所有人同意不得将文件中的内容挪作商业或盈利用途。
5. 人人文库网仅提供信息存储空间，仅对用户上传内容的表现方式做保护处理，对用户上传分享的文档内容本身不做任何修改或编辑，并不能对任何下载内容负责。
6. 下载文件中如有侵权或不适当内容，请与我们联系，我们立即纠正。
7. 本站不保证下载资源的准确性、安全性和完整性, 同时也不承担用户因使用这些下载资源对自己和他人造成任何形式的伤害或损失。
提示  人人文库网所有资源均是用户自行上传分享，仅供网友学习交流，未经上传用户书面授权，请勿作他用。
关于本文
本文标题：新型卫生筷子盒总体方案与传动机构设计【优秀】【word+4张CAD图纸】【毕设】
链接地址：https://www.renrendoc.com/p-315996.html

官方联系方式

网站客服网站客服      侵权投诉侵权投诉
1:下载资料失败解决办法   
2:不支持迅雷下载,请使用浏览器下载   
3:不支持QQ浏览器下载,请用其他浏览器   
4:下载后的文档和图纸-无水印   
5:文档经过压缩，下载后原文更清晰   
点击下载此资源
关于我们 - 网站声明 - 网站地图 - 资源地图 - 友情链接 - 网站客服 - 联系我们

网站客服QQ：2881952447     

copyright@ 2020-2025  renrendoc.com 人人文库版权所有   联系电话：400-852-1180

备案号:蜀ICP备2022000484号-2       经营许可证: 川B2-20220663       公网安备川公网安备: 51019002004831号

本站为文档C2C交易模式，即用户上传的文档直接被用户下载，本站只是中间服务平台，本站所有文档下载所得的收益归上传人(含作者)所有。人人文库网仅提供信息存储空间，仅对用户上传内容的表现方式做保护处理，对上载内容本身不做任何修改或编辑。若文档所含内容侵犯了您的版权或隐私，请立即通知人人文库网，我们立即给予删除！