人人文库网 > 图纸下载 > 毕业设计 > 电控气动机械手设计【四自由度】【6张图纸+毕业论文】【优秀】【原名教学型搬运机械手的设计】

外文翻译--气动肌肉伺服并联机构位姿自适应鲁棒控制的研究.doc

电控气动机械手设计【四自由度】【6张图纸+毕业论文】【优秀】【原名教学型搬运机械手的设计】

资源目录

电控气动机械手设计【四自由度】【6张图纸】【优秀】【原名教学型搬运机械手的设计】.rar

装配图.dwg---(点击预览)

电路图.dwg---(点击预览)

电控气动机械手设计【四自由度】说明书.doc---(点击预览)

手部.dwg---(点击预览)

手臂升降回转.dwg---(点击预览)

手臂伸缩手腕回转.dwg---(点击预览)

夹紧气缸缸体.dwg---(点击预览)

外文翻译--气动肌肉伺服并联机构位姿自适应鲁棒控制的研究.doc---(点击预览)

压缩包内文档预览：(预览前20页/共28页)

编号：422001 类型：共享资源大小：2.65MB 格式：RAR 上传时间：2015-04-01 上传人：上*** IP属地：江苏

39
积分

版权申诉 word格式文档无特别注明外均可编辑修改；预览文档经过压缩，下载后原文更清晰！ 立即下载

关键词：: 电控气动机械手设计四自由度图纸气动机械手教学型搬运机械手

资源描述：

电控气动机械手设计

46页 21000字数+说明书+6张CAD图纸【详情如下】

外文翻译--气动肌肉伺服并联机构位姿自适应鲁棒控制的研究.doc

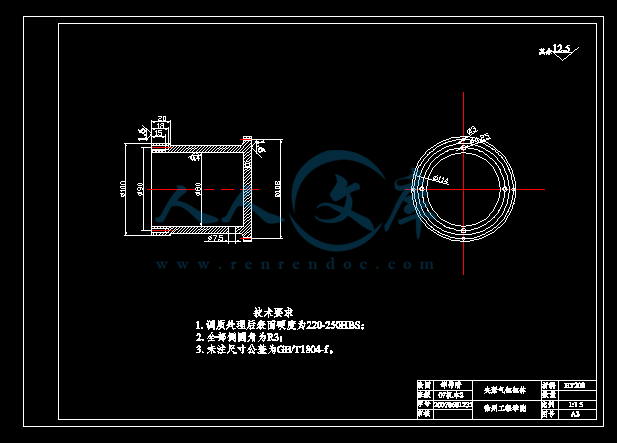
夹紧气缸缸体.dwg

手臂伸缩手腕回转.dwg

手臂升降回转.dwg

手部.dwg

教学型搬运机械手的设计（气动机械手的设计）.doc

电路图.dwg

装配图.dwg

QQ截图20131225174940.gif

QQ截图20131225175339.gif

电控气动机械手设计.gif

电路图.gif

夹紧气缸缸体.gif

手臂伸缩手腕回转.gif

手臂升降回转.gif

手部.gif

1 绪论1

1.1 机械手概述1

1.2 机械手的组成和分类1

1.2.1 机械手的组成1

1.2.2 机械手的分类4

1.3 国内外发展状况5

1.4课题研究的主要内容6

1.5教学用机械手的功能要求及现实意义6

1.5.1 教学用机械手的功能要求6

1.5.2 教学用机械手的现实意义7

2 机械手的设计方案8

2.1 机械手的座标型式与自由度8

2.1.1 机械手的坐标型式8

2.1.2 机械手的自由度9

2.2 机械手的手部结构方案设计9

2.3 机械手的主要参数11

2.4 机械手的技术参数列表11

3 机械手机械系统设计13

3.1 手部结构设计13

3.1.1 设计时考虑的几个问题13

3.1.2手爪夹持装置的机构选型13

3.1.3 手部夹紧气缸的设计15

3.2手腕结构设计19

3.2.1 手腕的自由度19

3.2.2 手腕的驱动力矩的计算19

3.3手臂结构设计23

3.3.1手臂伸缩与手腕回转部分23

3.3.2手臂升降和回转部分26

3.3.3手臂升降气缸的设计26

3.3.4手臂回转缸体的设计29

4机械手气压系统的设计31

4.1气压传动系统工作原理图31

4.2气动元件介绍31

5 机械手控制系统设计35

5.1 控制系统的结构分类35

5.2 控制方式35

5.3机械手的控制36

6 结论38

7致谢39

参考文献40

1 绪论

1.1 机械手概述

机器人由操作机(机械本体)、控制器、伺服驱动系统和检测传感装置构成，是一种仿人操作，自动控制、可重复编程、能在三维空间完成各种作业的机电一体化自动化生产设备。特别适合于多品种、变批量的柔性生产。它对稳定、提高产品质量，提高生产效率，改善劳动条件和产品的快速更新换代起着十分重要的作用。

机器人技术是综合了计算机、控制论、机构学、信息和传感技术、人工智能、仿生学等多学科而形成的高新技术，是当代研究十分活跃，应用日益广泛的领域。机器人应用情况，是一个国家工业自动化水平的重要标志。

机器人并不是在简单意义上代替人工的劳动，而是综合了人的特长和机器特长的一种拟人的电子机械装置，既有人对环境状态的快速反应和分析判断能力，又有机器可长时间持续工作、精确度高、抗恶劣环境的能力，从某种意义上说它也是机器的进化过程产物，它是工业以及非产业界的重要生产和服务性设各，也是先进制造技术领域不可缺少的自动化设备。

机械手是模仿着人手的部分动作，按给定程序、轨迹和要求实现自动抓取、搬运或操作的自动机械装置。在工业生产中应用的机械手被称为“工业机械手”。生产中应用机械手可以提高生产的自动化水平和劳动生产率:可以减轻劳动强度、保证产品质量、实现安全生产；尤其在高温、高压、低温、低压、粉尘、易爆、有毒气体和放射性等恶劣的环境中，它代替人进行正常的工作，意义更为重大。因此，在机械加工、冲压、铸、锻、焊接、热处理、电镀、喷漆、装配以及轻工业、交通运输业等方面得到越来越广泛的引用。

机械手的结构形式开始比较简单，专用性较强，仅为某台机床的上下料装置，是附属于该机床的专用机械手。随着工业技术的发展，制成了能够独立的按程序控制实现重复操作，适用范围比较广的“程序控制通用机械手”，简称通用机械手。由于通用机械手能很快的改变工作程序，适应性较强，所以它在不断变换生产品种的中小批量生产中获得广泛的引用。

1.2 机械手的组成和分类

1.2.1 机械手的组成

机械手主要由执行机构、驱动系统、控制系统以及位置检测装置等所组成。各系统相互之间的关系如方框图1-1所示。

图1-1机械手的组成方框图

(一)执行机构

它包括手部、手腕、手臂和立柱等部件，有的还增设行走机构。

1、手部

即与物件接触的部件。由于与物件接触的形式不同，可分为夹持式和吸附式手部。夹持式手部由手指(或手爪) 和传力机构所构成。手指是与物件直接接触的构件，常用的手指运动形式有回转型和平移型。回转型手指结构简单，构件制造容易，故应用较广泛。平移型应用较少，其原因是结构比较复杂，但平移型手指夹持圆形零件时，工件直径变化不影响其轴心的位置，因此适宜夹持直径变化范围大的工件。

手指结构取决于被抓取物件的表面形状、被抓部位(是外廓或是内孔)和物件的重量及尺寸。常用的指形有平面的、V形面的和曲面的:手指有外夹式和内卡式;指数有双指式、多指式和双手双指式等。

而传力机构则通过手指产生夹紧力来完成夹放物件的任务。传力机构型式较常用的有:连杆式、凸轮式、齿轮齿条式、螺旋式和绳轮式等。

吸附式手部主要由吸盘等构成，它是靠吸附力(如吸盘内形成负压或产生电吸磁力)吸附物件，相应的吸附式手部有负压吸盘和电磁盘两类。

对于轻小片状零件、光滑薄板材料等，通常用负压吸盘吸料。造成负压的方式有气流负压式和真空泵式。

对于导磁性的环类和带孔的盘类零件，以及有网孔状的板料等，通常用电磁吸盘吸料。电磁吸盘的吸力由直流电磁铁和交流电磁铁产生。

用负压吸盘和电磁吸盘吸料，其吸盘的形状、数量、吸附力大小，根据被吸附的物件形状、尺寸和重量大小而定。

2、手腕

是连接手部和手臂的部件，并可用来调整被抓取物件的方位(即姿势)。

3、手臂

手臂是支承被抓物件、手部、手腕的重要部件。手臂的作用是带动手指去抓取物件，并按预定要求将其搬运到指定的位置。机械手的手臂通常由驱动手臂运动的部件(如油缸、气缸、齿轮齿条机构、连杆机构、螺旋机构和凸轮机构等)与驱动源(如液压、气压或电机等)相配合，以实现手臂的各种运动。

机械手的技术参数列表

　　　一．用途:教学型机械手

　　　二．设计技术参数:

　　　1．抓重：10千克

　　　2．自由度数：4个自由度

　　　3．座标型式：圆柱型座标

　　　4．最大工作半径：1000mm

　　　5．手臂最大中心高：1380mm

　　　6．手臂运动参数

　　　伸缩行程400mm

　　　伸缩速度50mm/s

　　　升降行程200mm

　　　升降速度50mm/s

　　　回转范围00-2400

　　　回转速度900/s

　　　7．手腕运动参数

　　　回转范围 00-1800

　　　回转速度1800/s

　　　8．定位精度：±0. 5mm

　　　9.缓冲方式：液压缓冲器

　　　10．传动方式：气压传动

　　　11.控制方式：点位程序控制(采用单片机)

内容简介：: 徐州工程学院毕业设计外文翻译学生姓名学院名称机电工程学院专业名称机械设计制造及其自动化指导教师2011年5月27日英文原文Adaptive robust posture control of a parallel manipulator driven by pneumatic musclesKeywords:Pneumatic muscleParallel manipulatorAdaptive controlNonlinear robust controlAbstractRather severe parametric uncertainties and uncertain nonlinearities exist in the dynamic modeling of a parallel manipulator driven by pneumatic muscles. Those uncertainties not only come from the time-varying friction forces and the static force modeling errors of pneumatic muscles but also from the inherent complex nonlinearities and unknown disturbances of the parallel manipulator. In this paper, a discontinuous projection-based adaptive robust control strategy is adopted to compensate for both the parametric uncertainties and uncertain nonlinearities of a three-pneumatic-muscles-driven parallel manipulator to achieve precise posture trajectory tracking control. The resulting controller effectively handles the effects of various parameter variations and the hard-to-model nonlinearities such as the friction forces of the pneumatic muscles. Simulation and experimental results are obtained to illustrate the effectiveness of the proposed adaptive robust controller. 2008 Elsevier Ltd. All rights reserved.1. IntroductionPneumatic muscle is a new type of flexible actuator similar to human muscle. It is usually made up of a rubber tube and crossweave sheath material. Pneumatic muscles have the advantages of cleanness, cheapness, light-weight, easy maintenance, and the higher power/weight and power/volume ratios when compared with pneumatic cylinders (Ahn, Thanh, & Yang, 2004). The basic working principle of a pneumatic muscle is as follows: when the rubber tube is inflated, the cross-weave sheath experiences lateral expansion, resulting in axial contractive force and the movement of the end point position of the pneumatic muscle. Thus, the position or force control of a pneumatic muscle along its axial direction can be realized by regulating the inner pressure of its rubber tube. The parallel manipulator driven by pneumatic muscles (PMDPM) studied in this paper is a new application of pneumatic muscles.It consists of three pneumatic muscles connecting the moving arm of the parallel manipulator to its base platform as shown in Fig. 1. By controlling the lengths of three pneumatic muscles,three degrees-of-freedom (DOF) rotation motion of the parallel manipulator can be realized. Such a parallel manipulator combines the advantages of compact structure of parallel mechanisms with the adjustable stiffness and high power/volume ratio of pneumatic muscles, which will have promising wide applications in robotics,industrial automation, and bionic devices.Many researchers have investigated the precise position control of pneumatic muscles during the past several years.Most of them dealt with the control of single or antagonistic pneumatic muscles. Specifically, Bowler, Caldwell, and Medrano-Cerda (1996), employed an adaptive pole-placement scheme to control a bi-directional pneumatic muscle actuator system, for use on a 7-DOF anthropomorphic robot arm. Cai and Yamaura (1996)presented a sliding mode controller for a manipulator driven by artificial muscle actuators. Kimura, Hara, Fujita, and Kagawa(1997), applied the feedback linearization method to the position control of a single-input pneumatic system with a third-order dynamics including the pressure dynamics. Kimoto and Ito (2003)added nonlinear robust compensations to a linear controller in order to stabilize the system globally and achieve robustness to uncertain nonlinearities. Carbonell, Jiang, and Repperger (2001),Chan, Lilly, Repperger, and Berlin (2003), Repperger, Johnson, andPhillips (1998) and Repperger, Phillips, and Krier (1999), proposed several methods such as fuzzy backstepping, gain-scheduling,variable structure and fuzzy PD+I for a SISO pneumatic muscle system with a second-order dynamics to achieve asymptotic position tracking. Lilly (2003), Lilly and Quesada (2004) and Lilly and Yang (2005), applied the sliding mode control technique with boundary layer to control pneumatic muscle actuators arranged in bicep and tricep configurations. Tian, Ding, Yang, and Lin(2004), adopted the RPE algorithm to train neural networks for modeling and controlling an artificial muscle system. Hildebrandt,Sawodny, Neumann, and Hartmann (2002); Sawodny, Neumann,and Hartmann (2005), presented a cascade controller for a twoaxis planar articulated robotic arm driven by four pneumatic muscles.As reviewed above, some of the researchers designed robust controllers without considering the pressure dynamics, while the effect of pressure dynamics is essential for the precise control of pneumatic muscles (Carbonell et al., 2001; Chan et al., 2003; Lilly, 2003; Lilly & Quesada, 2004; Lilly & Yang, 2005; Repperger et al., 1998,1999). Some of the researchers developed controllers with the assumption that the system model is accurate, or that model uncertainties satisfy matching condition only, while those assumptions are hard to be satisfied in practice (Hildebrandt et al., 2002, 2005; Kimura et al., 1997). For the PMDPM shown in Fig. 1, it not only has all the control difficulties associated with the pneumatic muscles, but also the added difficulties of the coupled multi-input-multi-output (MIMO) complex dynamics of the parallel manipulator and the large extent of unmatched model uncertainties of the combined overall system. In other words,there exist rather severe parametric uncertainties and uncertain nonlinearities, which are caused not only by the time-varying friction forces and static force modeling errors of pneumatic muscles but also by the inherent complex nonlinearities and unknown disturbances of the parallel manipulator. Therefore, it is very difficult to control precisely the posture of the PMDPM.The recently proposed adaptive robust control (ARC) has been shown to be a very effective control strategy for systems with both parametric uncertainties and uncertain nonlinearities (Xu & Yao,2001; Yao, 2003; Yao, Bu, Reedy, & Chiu, 2000; Yao & Tomizuka,2001). This approach effectively integrates adaptive control with robust control through utilizing on-line parameter adaptation to reduce the extent of parametric uncertainties and employing certain robust control laws to attenuate the effects of various uncertainties. In ARC, a projection-type parameter estimation algorithm is used to solve the design conflict between adaptive control and robust control. Thus, high final tracking accuracy is achieved while guaranteeing excellent transient performance.In this paper, the posture control of a PMDPM shown in Fig. 1 is considered in which each pneumatic muscle is controlled by two fast switching valves. The adaptive robust control strategy is applied to reduce the lumped uncertain nonlinearities and parametric uncertainties while using certain robust feedback to attenuate the effects of uncompensated model uncertainties.In addition, pressure dynamics are explicitly considered in the proposed controller. Consequently, good tracking performance is achieved in practice as demonstrated by simulation and experimental results.The paper is organized as follows: Section 2 gives the dynamic models of the PMDPM controlled by fast switching valves. Section3 presents the proposed adaptive robust controller, along with proofs of the stability and asymptotic output tracking of the resulting closed-loop system. Section 4 shows the advantages of the proposed adaptive robust controller over the traditional deterministic robust controller via simulation results. Section 5 details the obtained experimental results to verify the effectiveness of the proposed adaptive robust posture controller and Section 6 draws the conclusions.2. Dynamic modelsThe PMDPM shown in Fig. 1 consists of a moving platform,a base platform, a central pole, and three pneumatic muscles.Pneumatic muscles are linked with the moving platform and the base platform by spherical joints Bi and Ai (i = 1, 2, 3) respectively.The joints are evenly distributed along a circle on the moving platform and the base platform respectively. The central pole is rigidly fixed with the base platform and is connected with the moving platform by a ball joint. Consider two frames, the first one,reference frame Oxyz fixed to the base platform, and the second one, moving frame O1x1y1z1 attached to the moving platform at the center (Tao, Zhu,&Cao, 2005). The posture of thePMDPMis defined through the standard RollPitchYaw (RPY) angles: first rotate the moving frame around the fixed x-axis by the yaw angle _x, then rotate the moving frame around the fixed y-axis by the pitch angle_y, and finally rotate the moving frame around the fixed z-axis by the roll angle _z. Two fast switching valves are used to regulate the pressure inside each pneumatic muscle, and this combination is subsequently referred to as a driving unit.Some realistic assumptions are made as follows to simplify the analysis: (a) The working medium of the pneumatic muscles satisfies the ideal gas equation, (b) Resistance and dynamics of various pipes of the pneumatic muscles are neglected, (c) The gas leakage from the pipe is neglected, and (d) The opening and closing time of the fast switching valves are also neglected.2.1. Dynamic model of parallel manipulator2.1.1. Inverse kinematics of parallel manipulatorLet the posture vector of the moving platform be=. Define as the position vector of the ith spherical joint of the base platform in frame Oxyz and as the position vector of the ith spherical joint of the moving platform in frame Oxyz. Let be the position vector of the center Oin frame Oxyz andthe position vector of the ith spherical joint of he moving platform in frame Oxyz. Then,+ （1）where is the rotational matrix from frame Oxyzto frame Oxyz and was uniquely determined using the posture vector by Huang, Kou, and Fang (1997) （2）where c and s are short-hand notations for cosand sinrespectively. The contractive length of the ith pneumatic muscle can then be determined as （3）where is the initial length of pneumatic muscle, is the ineffective length between the base platform and the moving platform excluding the effective length of the ith pneumatic muscle, and | | represents the Euclidean norm of a vector. Eq.(3) solves the inverse kinematics of the moving platform from the posture vector _ to the contractive length vector of three pneumatic muscles.2.1.2. Dynamics of parallel manipulatorLet be the value of the force acting on the moving platform by the ith pneumatic muscle along its axial direction, with positive value for the contractive force. Denote a force vector as F=. Let the angular velocity of the moving platform expressed in the base frame Oxyz be. Then, according to the dynamic equation of a rigid body, the dynamic model of the moving platform can be written as Tao et al. (2005) (4)where I（） is the rotational inertia matrix and Crepresents the Coriolis terms, represents the coefficient matrix of viscous frictions of the spherical joints, represents the external disturbance vector, and J()is the Jacobian transformation matrix between the contractive velocity vector of pneumatic muscles and angular velocity vector of the moving platform.The dynamic equations of the driving units can be written as （5）Where M=diag（）is the equivalent mass matrix of three pneumatic muscles and their spherical joints, F= is the friction force vector of pneumatic muscles,and is the static force vector of pneumatic muscles detailed in Section 2.2. Merging Eqs. (4) and (5) while noting and in which （G（）is the transformation matrix from the angular velocity vector to the posture velocity vector of the PMDPM via three RPY angles, the dynamic model of PMDPM can be obtained as follows in terms ofposture vector. （6）where+.2.2. Models of actuator2.2.1. Characteristics of pneumatic muscleFor each driving unit i, the static force of pneumatic muscle is(Chou & Hannaford, 1996; Tondu & Lopez, 2000; Yang, Li, & Liu,2002) （7）（8）where pis the pressure inside the pneumatic muscle, a and b are constants related to the structure of pneumatic muscle, kis a factor accounting for the side effect, is the contractive ratio given by=x/L, F is the rubber elastic force, D is the initial diameter of the pneumatic muscle, is the thickness of shell and bladder, E is the bulk modulus of elasticity of rubber tube with cross-weave sheath, is the initial braided angle of the pneumatic muscle, is the current braided angle of the pneumatic muscle given by and is the modeling error.2.2.2. Actuator dynamicsThe pressure dynamics that generates the pressure inside the pneumatic muscle will be given. Suppose the relationship between volume and pressure inside the pneumatic muscle can be described by polytropic gas law （9）where is the pneumatic muscles inner volume, which is a function of , is the air mass inside the pneumatic muscle, and is the polytropic exponent. The ideal gas equation describes the dependency of the air mass. （10）where R is the gas constant and Ti is the thermodynamic temperature inside the pneumatic muscle.Differentiate Eq. (9) while noting Eq. (10), one obtains （11）where is the air mass flow rate through the valve.Suppose in which qmi is the calculable air mass flow rate given in Section 2.2.3, and are the coefficient and disturbance considering model errors respectively.Then the following general pressure dynamic equation instead ofEq. (11) will be used (Richer & Hurmuzlu, 2000) （12）where 2.2.3. Valve modelThe relationship between the calculable air mass flow rate into the ith pneumatic muscle and control input (the duty cycle of two fast switching valves in the ith driving unit) can be put into the following concise form (Tao et al., 2005) （13）where is a nonlinear flow gain function given by =within which is the effective orifice area of fast switching valve, is the upstream pressure, pdi is the downstream pressure, is the upstream temperature and k is the ratio of specific heat.2.3. Dynamics in state-space formLet be the calculable and differentiable part of Fm. And define the drive moment of the PMDPM in task-space as （14）Differentiate Eq. (14) while noting Eqs. (12) and (13), the dynamics of actuators are described as （15）Where-=Define a set of state variables as x=.Then the entire system can be expressed in a state-space form as （16）where is the inverse function of Eq. (14) from to p,and. Note that both and are positive definite matrices. For the simplicity of notation, the variables such as and are expressed by and when no confusions on the function variables exist.3. Adaptive robust controller3.1. Design issues to be addressedGenerally the system is subjected to parametric uncertainties due to the variation of etc., and uncertain nonlinearities represented by and that come from uncompensated model terms due to complex computation, unknown model errors and disturbances etc. Practically, dp and d_ may be decomposed into two parts, the constant or slowly changing part denoted by and, and the fast changing part denoted by i.e., The main unknown parameters will be updated on-line through adaptation law to improve performance while the effects of other minor parameters will be lumped into uncertain nonlinearities. For simplicity, the following notations are used throughout the paper: i is used for the ith component of the vector , the operation for two vectors is performed in terms of the corresponding elements of the vectors, and denotes the uncertain parameter vector. Then, the following assumption is made as in Yao et al. (2000).Assumption: The extent of parametric uncertainties and uncertain nonlinearities are known, i.e. , whereis the maximum parameter vector, is the minimum parameter vector, and are known vectors.It can be seen that the major difficulties in controlling are:(a) The entire system is a highly nonlinear MIMO coupling dynamic system, due to either unknown disturbances, and nonlinear flow gains or nonlinear and time-varying terms such as. Therefore, it is more suitable to design a nonlinear controller based on the MIMO model instead of a linear controller based on linearization.(b) The system has severe parametric uncertainties represented by the lack of knowledge of damping coefficients Cs and the polytropic exponents and . Hence on-line parameter adaptation method should be adopted to reduce parametric uncertainties.(c) The system has large extent of lumped modeling errors like unknown disturbances and unmodeled friction forces, which are contained in and .So both on-line adaptation and effective robust attenuation to these terms should be used for good control performance.(d) The model uncertainties are unmatched, i.e., both parametric uncertainties and uncertain nonlinearities appear in the dynamic equations of the PMDPM that are not directly related to the control input u. Therefore, the backstepping design technology should be employed to overcome design difficulties for achieving nasymptotic stability.3.2. Projection mappingLet denote the estimate of and the estimation error. In view of Assumption, the following projection-type parameter adaptation law is used to guarantee that the parameter estimates remain in the known bounded region all the time (Yao et al., 2000). （17）（18）where is a positive definite diagonal matrix of adaptation rates and is a parameter adaptation function to be synthesized later.It can be shown that for any adaptation function, such a parameter adaptation law guarantees （19）3.3. ARC controller designThe design is carried out using the recursive backstepping design procedure via ARC Lyapunov functions in task-space and muscle-space as follows (Yao et al., 2000).(1) Step 1Define a switching-function-like quantity as （20）where is the trajectory tracking error vector and Kc is a positive definite diagonal feedback matrix. If converges to a small value or zero, then will converge to a small value or zero since the transfer function from to is stable. Thus the next objective is to design the drive moment for making as small as possible. For this purpose, define the unknown parameter vector in task-space as and denote the effects of parametric uncertainties in task-space as （21）where is a regressor given by ,with .The desired drive moment consists of two terms （22）where functions as the adaptive control part used to achieve an improved model compensation through on-line parameter adaptation via , and is a robust control law to be synthesized later. is updated by an adaptation law of the form Eq. (17), i.e., （23）with the parameter adaptation function given by .And consists of two terms （24）where is a positive definite feedback gain matrix. is synthesized to dominate the model uncertainties coming from both parametric uncertainties and uncertain nonlinearities, which is chosen to satisfy the following conditions. （25）where is a positive design parameter that can be arbitrarily small. How to choose to satisfy constraints like Eq. (25) can be found in Yao and Tomizuka (1997).Denote the input discrepancy as. Differentiate Eq.(20) and substitute Eqs. (22) and (24) into it while noting Eq. (16),then （26）Define two positive semi-definite (p.s.d) functions for robust control and for adaptive control. From Eq. (26), the time derivative of is （27）And the time derivative of is （28）When ,substitute the first equation of Eq. (25) into Eq. (27),one obtains （29）Thus, will exponentially converge to the ball and then be ultimately bounded. Furthermore, if the system is devoid of uncertain nonlinearities (i.e., ), substitute Eq. (23)and the second equation of Eq. (25) into Eq. (28) while noting Eq.(19), one obtains （30）Hence will asymptotically converge to zero and an improved steady-state tracking performance will be obtained.(2) Step 2The next step is to synthesize the air mass flow rate so that converges to a small value or zero with a guaranteed transient performance. For this purpose, first note that the unknown parameter vector in muscle-space is .Then the terms due to parametric uncertainties in muscle-space can be described by （31）where is the regressor for parameter adaptation, is updated by an adaptation law of the form Eq. (17), i.e., （32）with the parameter adaptation function given by .From Eqs. (15) and (22), the dynamics of is （33）where in which and are estimates of and respectively, and are deduced from by an output differential observer. Note that represents the calculable part of and can be used to design control input u, but cannot, due to various uncertainties. The desired mass flow rate is （34）where is used for adaptive model compensation and the robust ol law consists of the following two terms. （35）where is a positive definite feedback gain matrix and is a nonlinear robust feedback function chosen to satisfy the following conditions for dominating all model uncertainties. （36）中文译文气动肌肉伺服并联机构位姿自适应鲁棒控制的研究关键词：气动肌肉并联机构自适控制非线性鲁棒控制摘要：气动肌肉伺服并联机构的动态模型中存在着相当严重的参数不确定性和不确定非线性。那些不确定性不仅来自气动肌肉中随时间变化的摩擦力和静力建模误差,而且还有来自并联机构内部复杂的非线性和未知的干扰。在这篇论文中,采用非连续基于投影的自适应鲁棒控制方法来弥补三位气动肌肉伺服并联机构的参数不确定性和不确定非线性从而用轨迹跟踪控制实现精确的姿势。由此产生的控制器有效地处理了各种参数变化和难以模拟的非线性，例如气动肌肉的摩擦力。仿真和实验结果用来说明被提议的自适应鲁棒控制器的效果。1.引言气动肌肉与人类肌肉类似，是一种新型的灵活的执行机构。它通常是有橡皮管和横向摆动的外壳材料组成。气动肌肉和气缸比较时有清洁，便宜，重量轻，容易维护和更高的功率重量比和功率体积比（Ahn, Thanh, & Yang, 2004）。气动肌肉的基本工作原理如下：当橡胶管膨胀时, 横向摆动的外壳侧向扩张,引起气动肌肉末端轴向收缩和运动。因此,气动肌肉沿着它轴向的位置和力能由调节它的橡胶管内部压力来实现。在这篇论文中的气动肌肉伺服的并联机构(PMDPM)的研究是气动肌肉的新的运用。它由三个气动肌肉把并联机构的动臂连接到底下的平台,如图1。并联机构的三个自由度的旋转运动能由控制三个气动肌肉的长度来实现。这样的机械手联合了可调节刚度的并联机构的密实结构和气动肌肉的高功率体积比的优点，它将有希望广泛应用于机器人，工业自动化和仿生装置上。许多研究人员在过去几年里已经研究出气动肌肉位置的精确控制。他们中大多数处理气动肌肉的单个或对立的控制。特别的是，Bowler, Caldwell, and Medrano-Cerda (1996)采用可调节的极点配置方法去控制一个双向的气动肌肉执行系统，它应用在7-DOF拟人机器人的手臂上。Cai and Yamaura (1996)提出了滑模控制器驱动机械手的人造肌肉执行机构。Kimura, Hara, Fujita, and Kagawa(1997)应用反馈线性化方法对单个输入的包括压力动态的三阶的气动系统的位置控制。Kimoto and Ito (2003)为了稳定全局的系统和得到不确定非线性的鲁棒性，增加了对线性控制器的非线性鲁棒补偿。Carbonell, Jiang, and Repperger (2001),Chan, Lilly, Repperger, and Berlin (2003), Repperger, Johnson, and Phillips (1998) and Repperger, Phillips, and Krier (1999)提出了几个方法，例如失真反馈，增益调整，可变结构和对带二阶系统的单输入单输出的气动肌肉进行失真PD+I，用这些方法可以实现对位置的逐步跟踪。Lilly (2003), Lilly and Quesada (2004) and Lillyand Yang (2005)应用带边界层的滑模控制技术去控制带有二头肌和肱三头肌的气动肌肉制动器。, Tian, Ding, Yang, and Lin(2004)采用RPE算法训练神经网络去模拟和控制一个人工肌肉系统。Hildebrandt,Sawodny, Neumann, and Hartmann (2002); Sawodny, Neumann,and Hartmann (2005)为由四个气动肌肉伺服的两轴平面铰接的机器人手臂提出了一种梯级控制器。综述了以上,一些研究人员在设计鲁棒控制器时没有考虑到动态压力,然而动态压力对气动肌肉的的精确控制是有很大影响的(Carbonell et al., 2001; Chan et al., 2003;Lilly, 2003; Lilly & Quesada, 2004; Lilly & Yang, 2005; Repperger et al., 1998, 1999)。一些研究人员研究的控制器必须假定系统模型是精确的,或者模型的不确定性符合一定的规律,然而这些假设要成立在实践中是困难的(Hildebrandt et al., 2002, 2005; Kimura et al., 1997)。如图1显示的PMDPM,它不仅有所有关于气动肌肉控制的困难,而且成对的多输入多输出(MIMO)复杂的并联机构的动力学和很多非匹配的模型不确定性联合到整体的系统上增加了难度。换句话说, 存在着相当严重的参数不确定性和不确定非线性，这些不确定性不仅是由气动肌肉中随时间变化的摩擦力和静力建模误差引起,而且还有并联机构内部复杂的非线性和未知的干扰。因此，这是很难精确控制PMDPM的位姿的。最近提出的自适应鲁棒控制(ARC)被证明是一种对有参数不确定性和不确定非线性的系统非常有效控制方法（Xu&Yao,2001;Yao,2003;Yao,Bu,Reedy,&Chiu,2000;Yao&Tomizuka,2001）。这种方法通过利用即时参数的调整去降低参数不确定性的程度和应用一定的鲁棒控制方法来衰减各种不确定性的影响有效的结合了自适应控制和鲁棒控制。在自适应鲁棒控制中,一种投影型参数估计算法被用来解决设计自适应控制和鲁棒控制之间的冲突。因此,最终实现了高精度目标跟踪而且保证了良好的瞬态性能。在这篇文章中，图一中的PMDPM的位姿控制中，每个气动肌肉是由两个快速转换阀控制的。自适应鲁棒控制的方法用来减少许多不确定性非线性和参数不确定性，使用一定的鲁棒反馈去减少无补偿模型的不确定性的影响。此外,压力在被提出的控制器中是要被慎重考虑的。因此,在实践中良好的跟踪性能由仿真和实验结果被证明获得。论文的结构如下:第二节主要讲由快速转换阀控制的PMDPM的动态模型。第三节主要讲所提出的自适应鲁棒控制稳定性的证明和闭环系统的渐进跟踪。第四节主要讲通过仿真结果证明上面提出的自适应鲁棒控制器相对传统的鲁棒控制器的优势。第五节详细说明了用得到的实验结果来证明所提出的自适应鲁棒控制器的效果，第六节进行了总结。2.动态模型在图1显示的PMDPM包括一个移动平台,一个固定平台、中央杆、和三个气动肌肉。气动肌肉分别与移动平台和固定平台以Bi和Ai的球形节点连接。这些节点都分别沿移动平台和基地平台的一周均匀分布。中央杆牢牢的固定在固定平台上并且另一端用球形接头与移动平台连接在一起。建立两个坐标系,第一个,在固定平台中心建立定参考系Oxyz，第二个在移动平台中心建立动参考系O1x1y1z1 (Tao, Zhu,&Cao, 2005)。PMDPM的位姿是通过标准的笛卡尔坐标系确定的:第一个绕x轴旋转的动坐标系是笛卡尔坐标系的yaw，然后绕y轴旋转的动参考系是笛卡尔坐标系的pitch，最后绕z轴旋转的动参考系的是笛卡尔坐标系的roll。两个快速转换阀被用来调节气动肌肉的内部压力,这个结合后来也被当作驱动装置。下面的一些假设能够简化分析:(a)气动肌肉的使用介质满足理想气体的方程式;(b)气动肌肉的各个管道的阻力全部被忽略,(c)从管道内泄漏的气体被忽略,(d)在开启和关闭转换阀的时间也被忽略。2.1并联机构的动态模型2.1.1并联机构的逆运动学令移动平台的位置矢量为=，定义为Oxyz坐标系中固定平台球形节点的位矢，定义为Oxyz坐标系中移动平台球形节点的位矢，令为O在Oxyz坐标系中的位矢，令为移动平台的球形节点在Oxyz坐标系中的位矢。得到+ （1）这里的是O1x1y1z1坐标系对Oxyz坐标系的旋转矩阵，唯一由位姿确定它。（2）这的c和s分别是cos和sin的速记写法。气动肌肉的收缩长度由如下式子确定（3）这里的是气动肌肉最初的长度，是固定平台与移动平台之间除去气动肌肉有效长度的剩余长度，| |是矢量的欧几里得范数。式子（3）是移动平台的位矢与三个气动肌肉的收缩长度的逆运动学。2.1.2并联机构的动力学令为气动肌肉沿它的轴向作用在移动平台上的力，收缩力为正值。令力的矢量为F=.令移动平台相对定坐标系Oxyz的角速度为。根据刚体的动态方程，移动平台的动态模式能被写成 (4)这里的I（）是旋转性矩阵，C是科式角速度。代表了球形节点的粘性摩擦力的合矩阵。代表了外界干扰的矢量。J()是气动肌肉压缩速度的矢量和移动平台的角速度矢量。驱动装置的动态方程能被写成（5）这里的M=diag（）是三个气动肌肉和他们的球形节点的等价矩阵。F=是气动肌肉的摩擦力矩阵，是在2.2节中详细说明的气动肌肉的静力矩阵，合并式子（4）和式

温馨提示:
1: 本站所有资源如无特殊说明，都需要本地电脑安装OFFICE2007和PDF阅读器。图纸软件为CAD,CAXA,PROE,UG,SolidWorks等.压缩文件请下载最新的WinRAR软件解压。
2: 本站的文档不包含任何第三方提供的附件图纸等，如果需要附件，请联系上传者。文件的所有权益归上传用户所有。
3.本站RAR压缩包中若带图纸，网页内容里面会有图纸预览，若没有图纸预览就没有图纸。
4. 未经权益所有人同意不得将文件中的内容挪作商业或盈利用途。
5. 人人文库网仅提供信息存储空间，仅对用户上传内容的表现方式做保护处理，对用户上传分享的文档内容本身不做任何修改或编辑，并不能对任何下载内容负责。
6. 下载文件中如有侵权或不适当内容，请与我们联系，我们立即纠正。
7. 本站不保证下载资源的准确性、安全性和完整性, 同时也不承担用户因使用这些下载资源对自己和他人造成任何形式的伤害或损失。

人人文库网所有资源均是用户自行上传分享，仅供网友学习交流，未经上传用户书面授权，请勿作他用。