研制改进齿轮滚刀检测装置设计【6张图纸】【优秀】
收藏
资源目录

压缩包内文档预览:(预览前20页/共52页)
编号:422365
类型:共享资源
大小:1.19MB
格式:RAR
上传时间:2015-04-02
上传人:上***
认证信息
个人认证
高**(实名认证)
江苏
IP属地:江苏
39
积分
- 关 键 词:
-
研制
改进
齿轮滚刀
检测装置
设计
图纸
齿轮滚刀检测装置
- 资源描述:
-
研制改进齿轮滚刀检测装置设计
41页 14000字数+说明书+外文翻译+6张CAD图纸【详情如下】
丝杠组件.dwg
外文翻译--绝热高速切削有限元模型.doc
工作台零件.dwg
总装配图.dwg
研制改进一台齿轮滚刀检测装置说明书.doc
研制改进齿轮滚刀检测装置设计说明书.doc
箱体.dwg
纵向进给.dwg
零件立柱.dwg



目录
摘要I
AbstractII
第1章 绪论1
1.1 课题分析1
第2章 齿轮滚刀概述3
2.1 齿轮刀具的主要类型、工作原理和选用3
2.2 齿轮滚刀基本蜗杆4
2.3 齿轮滚刀的原理误差5
2.4 齿轮滚刀的重磨误差8
第3章 课题分析与检测装置总体方案设计11
3.1 检测装置总体方案设计11
3.1.1系统运动方式的确定11
3.1.2伺服系统的选择11
3.1.5设计方案的可行性分析13
第四章 机械部分设计14
4.1 步进电机的选用14
4.1.1 步进电机的计算14
4.1.2步进电机的选用14
4.2 滚动导轨的设计与尺寸确定15
4.2.1 滚珠导轨的选择16
4.2.2.滚动导轨的预紧18
4.2.3.额定寿命的计算18
4.2.4.载荷计算19
4.2.5.滚动体确定20
4.2.6 许用负荷验算20
4.2.7.滚动导轨的材料和热处理21
4.3 滚珠丝杠螺母副的设计与尺寸确定21
4.3.1滚珠丝杠螺母副的选用22
4.3.2滚珠丝杠螺母副的计算23
4.3.3 滚珠丝杠螺母副的验算26
4.4变速机构中齿轮的设计28
4.4.1 齿轮参数计算29
结论34
致谢35
参考文献36
摘要
在工业化发展的今天,各种机械产品层出不穷,精度要求不断提高。齿轮传动作为传动机构的重要组成部分,其精度高低直接影响产品质量。因此,提高齿轮传动精度成为了提高产品质量的一种方法。齿轮传动精度的高低主要受装配精度、齿轮制造精度两方面的影响
齿轮制造精度是由加工刀具来保证。而齿轮滚刀是加工齿轮的重要刀具,尤其是阿基米德齿轮滚刀在加工各种齿轮的过程中得到了广泛的应用。所以,对阿基米德齿轮滚刀精度的分析检测是非常有必要的。
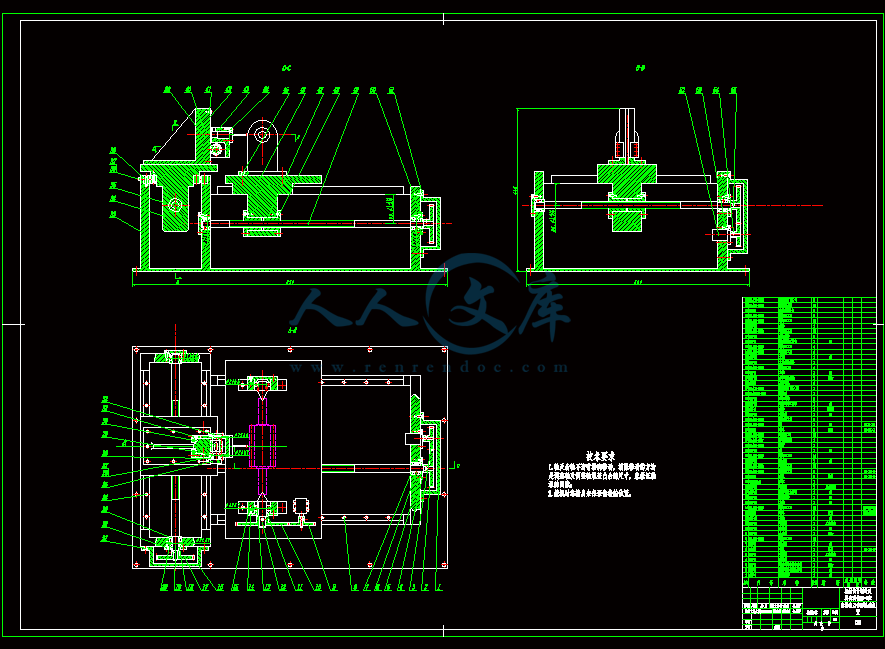
本设计主要任务是对零前角阿基米德齿轮滚刀的齿形误差进行检测。主要设计内容包括:检测装置总装配图,纵向进给装配图,箱体零件图,横向进给工作台零件图,立柱导轨零件图。
关键词 齿轮滚刀 齿形误差 检查仪 齿轮
第2章 齿轮滚刀概述
2.1 齿轮刀具的主要类型、工作原理和选用
齿轮刀具是用于加工齿轮齿形的刀具。由于齿轮的种类很多,其生产批量和质量的要求以及加工方法有各不相同,所以齿轮刀具的种类也很多,通常按下列的方法来分类:
2.1.1按被加工的齿轮类型分,有三类刀具:
1、圆柱齿轮刀具
(1)渐开线圆柱齿轮滚刀
如盘形齿轮铣刀、指形齿轮铣刀、齿轮拉刀、插齿刀盘、齿轮滚刀、插齿刀、梳齿刀和剃齿刀等
(2)非渐开线圆柱齿轮刀具
如圆弧齿轮滚刀、摆线齿轮滚刀和花键滚刀等。
2、蜗轮刀具
如蜗轮滚刀、蜗轮飞刀、蜗轮剃齿刀等
3、锥齿轮刀具
(1)直齿锥齿轮刀具
如成对刨刀、成对盘铣刀、拉—铣刀盘等
(2)曲线齿锥齿轮刀具
如弧齿锥齿轮铣刀盘、摆线齿锥齿轮铣刀盘等
2.1.2按刀具的工作原理分,有两类刀具
1、成形齿轮刀具
这类刀具的切削刃廓形与被加工的直齿齿轮端剖面内的槽形相同。这类刀具中有盘形齿轮铣刀、指形齿轮铣刀、齿轮拉刀、插齿刀盘等。用盘形或指形齿轮铣刀加工斜齿齿轮时,工件齿槽任何剖面中的形状都不和刀具的廓形相同,工件的齿形是由刀具的切削刃在相对于工件运动过程中包络而成的,这种加工方法称为无瞬心包络法。但由于这些刀具的结构和成形齿轮刀具相同,所以也将它们归纳在成形齿轮刀具一类之中。
2、展成齿轮刀具
这类刀具加工齿轮时,刀具本身好像也是一个齿轮,它和被加工的
- 内容简介:
-
I摘要摘要在工业化发展的今天 ,各种机械 产品层出不穷, 精度要求不断提高。齿轮传动作为传动机构的重要组成部分,其精度高低直接影响产品质量。 因此,提高齿轮传动精度成为 了提高产品质量 的一种方法。齿轮传动精度的高低主要受装配精度、齿轮制造精度两方面 的影响齿轮制造精度是由加工刀具来保证。而齿轮滚刀是加工齿轮的重要 刀具,尤其是 阿基米德 齿轮滚刀 在加工各种齿轮的过程中 得到了 广泛的应用 。所以,对阿基米德齿轮滚刀精度的分析检测是非常有必要的。本设计 主要任务是对零前角阿基米德齿轮滚刀的齿形误差进行检测。主要设计内容包括:检测装置总装配图,纵向进给装配图,箱体零件图,横向进给工作台零件图,立柱导轨零件图。关键词 齿轮滚刀 齿形误差 检查仪 齿轮IIAbstractIn industrialized development today, endless variety of mechanical products, the accuracy improved. Gear drive as a major component of its accuracy will directly affect the quality of products. Therefore, improving the precision gear drive into improving the quality of products of a rational design. Precision Gear mainly by the level of two aspects : the assembly of precision, the gear manufacturing precision. Gear manufacturing precision machining tool is to be guaranteed. And Hob processing gear is an important tool, Archimedes is particularly Hob in the processing of various gear the process to be widely used. Therefore, Archimedes Hob accuracy of detection is very necessary. The design is in this particular period of birth, Its main task is to zero angle before the Archimedes Hob profile error was detected. Keywords Hob profile error Tester Gear 1第 1 章 绪论随着国内工业化 的飞速 发展,如汽车 制造业,航空航天工业、造船业、机械装备制造业以及IT行业等的飞速发展 ,对各种工业产品的质量 提出了更高的要求 ,特别是各行业生产设备 。而衡量这些生产设备的质量 的好坏最重要的一点就是其性能。性能的好坏主要又是由构成设备的零部件精度决定的。所以,对零部件精度的掌握在一定程度上就体现出了 公司对产品质量 把握,决定了公司的效益。齿轮作为机械产品传动机构的重要组成部分,对机械产品的性能有很重要的影响。所以,各大 齿轮制造商在扩大齿轮产量、增加齿轮 品种的同时,更加注重提高齿轮质量。影响齿轮质量的因数很多,最直接的因数就是齿轮的加工刀具。齿轮滚刀是加工齿轮的重要 刀具,尤其是 阿基米德 齿轮滚刀 在加工各种齿轮的过程中得到了广泛的应用 。因此, 研究阿基米德齿轮滚刀的 测量技术和 研制相应的检测 仪器是非常必要的。在早期的生产中,检测齿轮 加工刀具 是否达到自己所希望的精度,通常用的是 手动测量 装置。不仅检测精度很难保证, 而且工作效率低,越来越难满足人们生产需要。随着机械工业和电子信息技术的发展与融合,我们把传感器、脉冲电机等电子设备与机械机构相结合得到了 检测更精确, 工作效率更高的齿轮 加工刀具 误差测量仪。本设计 主要是对零前角阿基米德齿轮滚刀的齿形误差进行检测。由于在设计中采用了先进的机械电子技术 ,提高了 设备检测精度与 生产效率 。所以,我们相信本设计的产品一定会比早期的产品更适合工业化生产。1.1 课题分析1.1.1设计目标研制、改进一台齿轮滚刀检测装置。设计参数:模数 m6、齿形角a20、前角0、加工齿轮精度 8级1.1.2拟解决的关键问题1、拆装方便、灵活;2、精度高,从简化结构方面提高精度。1.1.3研究内容21、检测装置的横向和纵向运动的实现;2、检测装置精度如何保证;3、被测滚刀定位夹紧 装置的确定 。3第2 章 齿轮滚刀概述2.1 齿轮刀具的主要类型、工作原理和选用齿轮刀具是用于加工齿轮齿形的刀具。由于齿轮的种类很多,其生产批量和质量的要求以及加工方法有各不相同,所以齿轮刀具的种类也很多,通常按下列的方法来分类:2.1.1按被加工的齿轮类型分,有三类刀具:1、圆柱齿轮刀具(1)渐开线圆柱齿轮滚刀如盘形齿轮铣刀、指形齿轮铣刀、齿轮拉刀、插齿刀盘、齿轮滚刀、插齿刀、梳齿刀和剃齿刀等(2)非渐开线圆柱齿轮刀具如圆弧齿轮滚刀、摆线齿轮滚刀和花键滚刀等。2、蜗轮刀具如蜗轮滚刀、蜗轮飞刀、蜗轮剃齿刀等3、锥齿轮刀具(1)直齿锥齿轮刀具如成对刨刀、成对盘铣刀、拉铣刀盘等(2)曲线齿锥齿轮刀具如弧齿锥齿轮铣刀盘、摆线齿锥齿轮铣刀盘等2.1.2按刀具的工作原理分,有两类刀具1、成形齿轮刀具这类刀具的切削刃廓形与被加工的直齿齿轮端剖面内的槽形相同。这类刀具中有盘形齿轮铣刀、指形齿轮铣刀、齿轮拉刀、插齿刀盘等。用盘形或指形齿轮铣刀加工斜齿齿轮时,工件齿槽任何剖面中的形状都不和刀具的廓形相同,工件的齿形是由刀具的切削刃在相对于工件运动过程中包络而成的,这种加工方法称为无瞬心包络法。但由于这些刀具的结构和成形齿轮刀具相同,所以也将它们归纳在成形齿轮刀具一类之中。2、展成齿轮刀具这类刀具加工齿轮时,刀具本身好像也是一个齿轮,它和被加工的齿轮各自按啮合4关系要求的速比传动,而由刀具齿形包络出齿轮的齿形。这类刀具中有齿轮滚刀、插齿刀、梳齿刀、剔齿刀、加工非渐开线齿形的各种滚刀、蜗轮刀具和锥齿轮刀具等,展成齿轮刀具的一个基本特点是通用性比成形 齿轮刀具好,也就是说:用 同一把展成齿轮 刀具,可以加工模数和齿形角相同而齿数不同的齿轮,也可用标准刀具加工不同变位系数的变位齿轮。根据不同的生产要求和条件,选用结合市的齿轮刀具是很重要的。在以上所说的各类齿轮刀具中,要数加工渐开线圆柱齿轮的刀具应用最广泛;而在这类刀具中,又以齿轮滚刀最为常用;因为他的加工效率较高,也能保证一般齿轮的精度要求,而且他既能加工外啮合的直齿齿轮,也能加工外啮合的斜齿齿轮。2.2 齿轮滚刀基本 蜗杆齿轮滚刀一般是指加工渐开线齿轮所用的滚刀。它是按螺旋齿轮啮合原理加工齿轮的。由于被加工的齿轮是渐开线齿轮,所以它本身应具有渐开线齿轮的几何特征。齿轮滚刀从其外貌看来并不像齿轮,实际上它是仅有一个齿(或两、三个齿)、但齿痕长而螺旋角很大(一般为 80以上,接近90)的斜齿圆柱齿轮。因为他的齿很长而螺旋角又很大,可以绕滚刀轴线转好几圈,因此从外貌上看,它很像一个螺杆,如图2-1中所示。为了使这个蜗杆能起切削作用,需沿其长度方向开出好多容屑槽(直槽或螺旋槽),因此把蜗杆上的螺纹割成许多较短的刀齿,并产生了前刀面2和切削刃3。每个刀齿有一个顶刃和两个侧刃。为了使刀齿有后角,还要用铲齿方法铲出后刀面4和顶后刀面1。但是各个刀齿的切削刃必须位于这个相当于斜齿圆柱齿轮的蜗杆的螺纹表面上,因此这个螺杆就称为滚刀的基本蜗杆。基本蜗杆的螺纹通常做成右螺旋的,有时也做成左螺旋的。基本蜗杆的螺纹表面若是渐开螺旋面,则称为渐开线基本蜗杆,而这样的滚刀称为渐开线滚刀。用这种滚刀可以切出理论上完全理想的渐开线齿轮。但这种滚刀制造困难,生产中很少采用,而是采用易于制造的近似齿形滚刀,如阿基米德滚刀和法向直廓螺旋面。这两种螺纹表面在端剖面中的截形不是渐开线,而是阿基米德螺线和延长渐开线。当滚刀的分圆柱导程角较小时,这种蜗杆与渐开线蜗杆非常近似,所以用近似齿形滚 刀切出的齿轮齿形虽然理论上不是渐开线,但误差是很小的。51-顶后面 2-前刀面3-切削刃 4-侧后刀面图 2-1 齿轮滚刀的基本蜗杆2.3 齿轮滚刀的原理误差生产中普遍使用的齿轮滚刀 是阿基米德滚刀。但是它与渐开线滚刀相比,其齿形是有误差的。这个误差 就是由于其基本蜗杆是阿基米德蜗杆,而不是渐开线蜗杆。当这两种蜗杆的模数、螺纹头数、分圆柱直径、法向齿形角、导程、齿厚和齿高等都分别相同时,那么唯一不同的就是齿形。以轴向齿形来说,渐开线蜗杆的轴向齿形是曲线(图2-2中的虚线),而阿基米德蜗杆的轴向齿形是直线(图2-2中实线) 。这两 种齿形相切于分圆柱面上。由此可知,若以渐开线滚刀为基准,则阿基米德滚刀的齿形在分圆柱面 上的误差为零,但越到齿顶盒齿根误差越大。图中的和分别为齿顶 和齿根处xafxif的最大轴向齿形误差。6图 2-2 两种轴向齿形的比较用滚刀加工齿轮 时,滚刀和工件相当于一对螺旋齿轮啮合,滚刀的齿形误差试验奇迹圆柱且平面内的啮合线方向传递到工件上去的。这个切平面与渐开线基本螺杆螺纹表面的交线是一条直线 A(图2-3) ,它与蜗杆端面的夹角等于基圆柱导程角;而这个切b平面与阿基米德基本蜗杆螺纹表面的交线是一条曲线B,它与直线A在分圆柱 面上相切。图中的和分别为阿基米德滚刀在齿顶盒齿根处的最大法向齿形误差。由 图nafnif2-2可知,大于,所以通常就把称为阿基米德滚 刀的齿形误差。nifnafnif阿基米德滚刀基本蜗杆的分圆柱导程角越小,则其齿形误差越小,如图 2-4的0曲线所示,所以精加工用的阿基米德齿轮滚刀通常做成较大的分圆柱直径,目的就是使其导程角较小,从而减少滚刀的齿形误差。有图2-2和图2-3可以看出,阿基米德蜗杆的螺纹在齿顶和齿根处都比渐开线蜗杆的螺纹宽一些,所以用阿基米德滚刀切出的齿轮齿形与正确的渐开线齿轮齿形相比,在齿顶和齿根处就窄一些,这就使得齿轮的齿顶部分以及齿根部分得到轻微的修形,因而对于高速重载齿轮能啮合时的干涉和噪音。7图 2-3 阿基米德滚刀齿形误差8图 2-4 齿形误差与导程角的关系2.4 齿轮滚刀的重磨误差1.滚刀重磨齿轮滚刀使用久了就会磨损。使用磨损了的齿轮滚刀加工齿轮时,会降低被加工齿轮的齿形精度和恶化表面质量,还会加剧机床的震动。滚刀的磨损量在粗切时超过0.81mm或精切时超过0.20.5mm,就需要重磨前刀面。滚刀的重磨精度对于滚刀的齿形精度有很大影响,必须十分重视。直槽滚刀的前刀面是平面,可以用直母线的锥形9砂轮来重磨。图 2-5是重磨滚刀时砂轮 的位置,需要样板来对准,使砂轮的锥面母线方向通过滚刀轴线。图 2-5 零前角滚刀刃磨时砂轮的相对位置2.重磨误差重磨或刃磨滚刀时可能产生的误差主要有三项:(1)前刀面径向误差 这是因为砂轮和滚刀的相对位置调整不准确而引起的。由于前刀面不通过滚刀轴线 ,使刀齿的齿形发生了畸变,而加工出来的齿轮齿形也产生了误差。(2)前刀面与滚刀轴线的平行性误差 这是因为滚刀在磨刀机床上的安装误差引起的。这种误差会使滚刀各刀面的侧刃依次而逐渐地离开正确的基本蜗杆表面,而顶刃的外径也形成锥度。这样的滚刀切出的齿轮齿形会向一侧歪斜,使牙齿的两侧齿形不对称。10(3)圆周齿距误差 这是因为磨刀 机床的分度机构不准确而引起的。滚刀的 侧后刀面是经过铲磨的,当圆周齿距不相等时,各刀齿的齿厚就大小不均匀,因而各侧刃就在同一个基本蜗杆的螺纹表面上,这样就造 成工件上不规则的齿形误差。11第3章 检测装置总体方案设计3.1 检测装置总体方案设计系统总体方案设计内容包括: 系统运动方式的确定。 伺服系统的选择。 执行机构得结构及传动方式的确定。3.1.1系统运动方式的确定数控系统按运动方式可分点位控制系统、点位直线系统、连续控制系统。点位控制系统是指被控制件由一点到另一点快速准确定位 ,却不能在两点之间工作的 系统; 点位直线系统是指被控制件沿平面内平行于导轨作直线工作的系统;连续控制系统是指被控制件沿平面内任何曲线都能工作的系统。点位控制系统造价低廉,适用于两点之间快速点位的系统;连续控制系统造价高,适用于连续工作的系统;点位直线系统造价介于前两者之间,适用于简单直线运动。由于齿轮滚刀齿形是直线 ,检测齿形误差只需沿直线运动,所以选择 点位直线 控制系统。3.1.2伺服系统的选择开环伺服系统在负荷不大时多采用功率步进电机作为伺服电机,开环控制系统由于没有检测反馈部件,因而不能纠正系统的传动误差,但开环系统结构简单、调整维修容易、在速度和精度要求不太高的场合得到广泛应用。闭环伺服系统具有在设备移动部件上得检测反馈元件来检测实际位移量,能补偿系统的传动误差。因而伺服控制精度高,闭环系统造价高、结构和调试较复杂,多用于精度要求高的场合。此仪器属于测量仪器,其分辨率为 0.005mm,所测齿轮滚刀加工的齿轮精度:8级,所以采用闭环伺服系统3.1.3执行机构的确定为保证数控系统得传动精度和工作平稳性。在设计机械传动装配时,通常采用低摩擦、低惯量、高刚度、无间隙、高谐振以及有适宜的阻尼比要求的传动方式。考虑12以上几点,本设计 采用以下措施:1、尽量采用低摩擦的传动和导向元件。如采用滚珠丝杠螺母副,滚动导轨等。2、提高系统的传动刚度,如应用预加负载的滚动导轨和滚珠丝杠传动副。丝杠支承设计成两端轴向固定,并加预拉伸的结构等提高传动刚度。3.1.4系统的工作原理阿基米德齿轮滚刀轴截面的齿形是直线。要形成直线轨迹只须两个方向的运动,如图3-1。所以只要两个方向的速度成一定比例关系。如图3-1。两个方向速度的比例 关系由程序控制 。图3-1 X轴与Y轴速度关系具体结构如图3-2。左右 方向进给都采用步进电机驱动滚珠丝杆,配合滚珠导轨形成平面运动。由于垂直方向精度要求不高,所以垂直方向采用齿轮齿条配合手动进给。13图3-2 齿轮滚刀检测装置结构3.1.5设计方案的可行性分析在本设计装置中,关键 问题有:1、横向、纵向 进给精度的保证 ;2、20斜线轨迹的形成 ;3、被测齿轮滚刀在装置中分度精度的保证。通过对以上问题的分析 采用以下相应的措施:1、采用步进电机驱动丝杠,带动工作台运动;2、采用横向、纵向速度匹配,形成平面内各种运动;3、采用脉冲步进电机保证分度精度。通过对机械原理课程的学习分析得出装置原理可行;通过对机械设计课程的确学习分析得出装置结构可行;通过对机械工程学的确学习分析得出装置工艺可行。14第四章 机械部分设计4.1 步进电机的选用4.1.1 步进电机的 计算1.步进电机的步距角 b取系统脉冲当量 p=0.005mm/step,初选步进电机步距角 b度。2.步进电机启动力矩的计算设步进电机等效负载力矩为 T,负载力为P,根据能量守衡原理,电机所做的功与负载力所做的功有如下关系。 TPS式中电机转角S移动部件的相对位移机械传动效率若取= b,则S= p,且 ,所以 (4-1)式中 p移动部件负载( N) ;G移动部件重量;P与重力方向一致作用在移动部件上的负载力;导轨摩擦系数;b步进电机步距角( rad) ;T电机轴负载力矩 (Ncm)本设计中,取0.003(淬火钢珠导轨的摩擦系数),0.96,P 200N,P z为0。所以:4.1.2步进电机的选用通过以上计算选择电机 45BF3-3A,步距角 b=0.9,额定负载转矩 T=98N.mm外36()()2pZbPGPTN cm 36 0.0052000.03 (2000)6.82 .20.9 0.96TN cm()ZPPGP15形LD=6345mm。4.2 滚动导轨的设计与尺寸确定在相配的两导轨面间放置滚动体或滚动支承,使导轨面间的摩擦性质成为滚动摩擦,此为滚动导轨,它的最大优点是摩擦因数小,动、静摩擦因数差小,因此,运动轻便灵活,运动所需的功率小,摩擦发热少、磨损小,精度保持性好,低速运动平稳性好,移动精度和定位精度高。滚动导轨还具有润滑简单(有时可以油脂润滑),高速运动时不 会像滑动导轨那样因动压效应而使导轨浮起等优点。但滚动导轨结构比较复杂、制造 比较困难、成本比较高、抗震性比较差。对灰尘比较敏感,因此必须 有良好的防护。4.2.1 滚珠导轨的特点滚动导轨广泛的应用于各种类型机床和机械。每一种机床和机械都利用了它的某些特点。例如:数控机床、坐标镗床、仿形机床和外圆磨床砂轮架导轨等,采用滚动导轨是为了实现低速平稳无爬行和精确位移,工具磨床的工作台采用滚动导轨,为了防止高速时因动压效应使工作台浮起来,以便提高加工精度,立式车床工作台采用滚动导轨是为了提高速度,等等。滚动导轨的类型很多,按运动轨迹分有直线运动导轨和圆运动导轨;按滚动体的形式分有滚珠、滚珠和滚针导轨;按滚动体是否循环可分为 滚动体循环和滚动体不 循环导轨。滚动导轨类型、特点及应用见表 4-2。表4-2滚动导轨类型、特点及应用类型特点及应用滚珠导轨行程不能太长,摩擦阻力小、刚度低、承载能力差,不能承受大的颠覆力矩和水平力;这种导轨适用于载荷不超过 1000N的机床,如工具磨床滚柱导轨载荷能力及刚度比滚珠导轨高,交叉滚珠导轨副四个方向均能承载滚动体不循环的滚动导轨滚针导轨滚针导轨承载能力最高 ;滚柱、滚针对导轨面的平行度误差要求比较敏感,且容易侧向偏移和滑动;主要用于承载能力较大的机床上。如立式车床,磨床等16滚动直线导轨副滚柱交叉导轨副滚柱导轨块滚动直线导轨套副滚动花键副有专业化生产厂生产品种规格比较齐全、技术质量保证。设计制造机器采用这类导轨副,可缩短设计制造周期、提高质量、降低成本。滚动体循环的滚动导轨滚动轴承滚动导轨任何能承受径向力的滚动轴承(或轴承组 )都可以作为这种导轨 的滚动元件轴承的规格多,可以设计成任意尺寸和承受能力的导轨,导轨行程可以很长很适合大载荷、高刚度、行程长的导轨,如大型磨头移动式平面磨床、绘图机等导轨 4.2.1 滚珠导轨的选择此设计为齿轮误差检测装置,属于高精度的检测仪器,所以采用滚珠导轨而不是滑动导轨,根据设计的需要和各种不同导轨的优缺点,决定采用滚珠导轨其结构如图4-1所示。17图4-1 滚珠导轨原理图在原理图中可以看到在 V型槽( V型槽一般为90)中安装了滚珠,为了防止滚珠滑落,安装了保持架,并且保持架可以保证各个滚珠之间的相对位置。之所以选择V形滚珠导轨是因为它的工艺性好,容易达到较高的加工精度。但滚珠导轨在工作时滚珠和导轨间是点接触,应力比较大,容易压出沟槽,所压沟槽的深度若不均匀,将会降低导轨的刚度及精度。为了改善这种情况,可采用以下的工艺:1、在V形槽与滚珠接触处预先研磨出一窄条圆弧面的浅槽,从而增加了滚珠与滚到的接触面积,提高了承载能力和耐磨性,但这种工艺的缺点是导轨中的摩擦力略有增加。2、采用双圆弧滚珠导轨,这种导轨是把导轨的滚道改为为圆弧形滚道,以增大滚动体与滚道接触点的曲率半径,从而提高了导轨的承载能力,以及刚度、使用寿命。但双圆弧导轨由于形状的特殊性也有它本身的不足:形状复杂,工艺较差,摩擦力较大。因此当精度要求很高时不易满足使用要求。在工程设计中为使双圆弧滚珠导轨能发挥接触面积较大,变形较小的优点,又不至于过分增大摩擦力,一般都根据经验把其参数控制在一个合理的范围内,在此设计中,由于滚珠导轨在工作时承受的力为 130N,相对于滚珠到过的极限力来说是很小的,所以在此设计中不需那样的计算。184.2.2.滚动导轨的预紧使滚动体与滚道表面产生初始接触弹性变形的方法称之为预紧。预紧导轨刚度比没有预紧的刚度大,在合理的预紧条件下,导轨磨损比较小,预紧的主要方式有:1、采用过盈装配形成预加负载:装配导轨时,根据滚动体的实际尺寸,刮研压板与滑板的结合面或在其间加上一定厚度的垫片,从而形成包容尺寸;过盈有一个合理的数值,达到此数值时,导轨刚度较好,而驱动力又不至于过大。2、用移动导轨板的方法实现预紧:预紧时先松开导轨体的连接螺钉,然后拧动侧面螺钉,即可调整导轨两边的距离而预紧。此外,也可用斜镶条来调整,这样导轨的预紧量沿全长分布比较均匀,故也常采用。由图4-1可以看到在本设计中采用的是第二种预紧方法。4.2.3.额定寿命的计算滚动直线导轨副额定寿命的计算与滚动轴承基本相同。 (4-2)maxpF式中L额定寿命( km) ;额定动载荷( KN) ;aCP当量动载荷( KN) ;受力最大的滑块所受的载荷 (KN) ; maxFZ导轨上的滑块数;指数,当滚动体为滚珠时 3;当为滚柱时, 103;额定寿命单位( km) ,滚珠时, K50km;滚柱时, K100km;硬度系数 1;hf温度系数,查文献 实用机床 设计tf手册表3.17-46;取1;()htcaawf f f f CLKfP19接触系数,查文献 实用机床设 计手册 表3.17-47;取1.00;cf精度系数,查文献 实用机床设计手册 表3.17-48;取0.9;af载荷系数,查文献 实用机床设计手册 表3.17-49。取1.2;wf由式( 4-2)可得4.2.4.载荷计算当导轨水平放置的时候主要载荷就是移动部分的重量,根据此装置设计意图和材料的密度及体积关系可估算移动部件的重量:33107.8 1010373G = (2.5+0.55+1+0.45+0.4+0.24)再加上其他元件的重量,则移动部分的总重量为400N。所以每一个导轨上的载荷为 200N。此外,摩擦阻力受结构形式、润滑剂的黏度、载荷及运动速度的影响而略有变化,预紧后,摩擦力稍微增大,摩擦力 (4-3)式中滚动摩擦系数, =0.0030.005;F法向载荷( N)密封件阻力 (N),每个滑块座 (=2N) ;ff取=0.005,则:F=2(0.005200+2)=6N;4.2.5.滚动体确定滚动体的尺寸和个数应根据单位接触面积上的容许压力计算确定。在一般条件下,应优先选用直径较大的滚动体,这是因为增大滚动体直径可以提高导轨的承载能力,对于滚珠导轨,其滚珠数目与承载能力及滚珠直径d0的平方成正比,因此增大 滚珠直径d03191 1 1 0.910605()()502.5 10 ()1.20.01htcaawf f f f CLKkmfP FFf20比增加滚珠数目有利,如果滚动体的数目 太少会降低导轨的承载能力,制造误差将 显著的影响运动件的位置精度;滚动体数目太多,则会增发负载在滚动体上的分布不均匀性,反而会降低刚度。实验表明,为使各滚动体承受的载荷比较均匀、合理的滚动体的数目为: (4-4) 式中 G为导轨所承受的运动组件的重力(N) ;d0为滚珠直径。在此选用导轨钢珠 d0=8mm。取整Z=14,根据实际情况在导轨的各边安装滚珠数目为7个。4.2.6 许用负荷验算平均每个滚珠上最大负载 式中PH导轨的预加载荷,按最大工作负荷的 1/2计算。现根据最大工作负载取PH=3N。则 max10.25PN许用负荷查文献 机械设计手册 表9.3-56得k=60N/cm2,查表得=1,则:2 60 (6/10)121.6()pN /22HGPGP(3400/2)143.52GP0/9.5ZGd400/9.5 814.9Zmax/GPPZ2 pkd21max10.25 Pp由此可知,此选择的导轨可用。4.2.7.滚动导轨的材料和热处理适用于滚动导轨的材料必须满足硬度高,性能稳定以及良好加工性能的特性,低碳合金钢如20Cr,经渗碳淬火,表面硬度可达 6063HRC;合金结构钢,如 40Cr,淬火后低温回火,硬度可达 4550HRc,加工性能良好,但硬度较低;合金工具钢,淬火之后低温回火,硬度可达 6064HRC,这种材料性能稳定,可以制造变形小,耐磨性高 的导轨;氮化钢,经调质或正火后,表面氮化,可得到很高的表面硬度(850HV) ,但硬化层很薄,加工成本高;铸铁,硬度可达到230240HBS,加工方便, 滚动体用滚 珠,一般可满足使用要求,在此装置中的滚动导轨的材料选用铸铁导轨。滚动体的材料一般采用滚动轴承钢(GCr15) ,淬火后硬度可达到 6066HRC。4.3 滚珠丝杠螺母副的设计与尺寸确定滚珠丝杠副传动与滑动丝杠传动相比其主要特点是:1、传动效率高 一般可达95%以上是滑动丝杠传动的 24倍;2、运动平稳,摩擦力小、灵敏度高、低速无爬行;3、可以预紧、消隙丝杠副的间隙,提高轴向接触刚度;4、定位精度和重复定位精度高;5、使用寿命为普通滑动丝杠的 46倍甚至更高;6、同步性好,用几套相同的滚珠丝杠副同时传动时传动几个相同的部件或装置时,可获得较好的同步性;7、使用可靠、润滑简单、维护方便;8、不自锁,可逆向传动,即螺母为主动,丝杠为被动。旋转运动变为直线运动;9、由专业厂生产,选用配套方便。滚珠丝杠副作为精密、高效的传动元件在精密机床、数控机床得到广泛应用,在机械工业、交通运输、航天航空、军工产品等各个领域应用得很普遍,可用作精密定位自动控制、动力传递和运动转换。4.3.1滚珠丝杠螺母副的选用1、滚珠丝杠螺母副的特点22滚珠丝杠螺母副的滚珠循环方式一般分外循环和内循环两种。外循环过程中滚珠与丝杠脱离接触,目前使用插管完成滚珠循环的结构,工艺性好,结构简单,但滚道管子突出于螺母外表,所以外循环丝杠螺母径 向尺寸较大。对于内循环方式,滚珠丝杠螺母副在循环过程中滚珠始终保持与丝杠接触。这时在左、右螺母上各装2个回珠反向器,它迫使滚珠越过丝杠的螺母外径,进入相邻的螺纹滚道,滚珠经过不到一圈即返回。 内循环滚珠丝杠螺母副工作滚珠数目少,流畅性好,摩擦损失小,传动效率高,径向 尺寸紧凑,轴向刚度好,但回珠器槽形复杂,需三坐标数控机床才能加工。滚珠丝杠 螺母副可以通过左右螺母的相互离开和相互靠近达到 消除间隙的 目的;当有过盈时, 即为预紧。常用的消除间隙或预加载的办法如下:(1)螺丝式调隙结构。2个螺母中的1个带有外伸螺纹套筒, 2个螺母均装有平健用来防止转动。用转动外伸螺纹套筒上的 2个锁紧螺母的方法来调整间隙和加预载。这种结构的优点是结构紧凑,工作可靠,调整方便,被广泛应用,但调隙量不易精确。(2)垫片式调隙结构。通过改变调整垫片的厚度,使 2个螺母产生相对位移,用以消除间隙,并产生预紧力。这种结构的优点是结构简单可靠,刚性好,装卸方便,特别是将垫片做成半环结构时,修磨再装就很方便。(3)齿差式调隙结构。在两个螺母的外凸缘上加工出两个齿轮(齿数差为1) 。这两个齿轮分别与螺母两 端的两个内齿圈相啮合 .内齿圈用螺钉紧固在螺母座上。只要转动其中一个螺母,就会使两个螺母的相对位置发生变化,以调整轴向间隙和预紧力。由于此检查装置工作负载很小,冲击力几乎为零,所以选用内循环、浮动反向器式滚珠丝杠螺母副。其浮动式的优点是:具有较好的摩擦特性,预紧力矩为固定反向器的1/31/4,在预紧时,预紧力上升平缓,适用于各种高灵敏、高刚度的精密进给定位系统。重载荷、多头螺纹、大导程不宜采用。同时为了满足滚珠丝杠的定位及预紧,特设计一对滚珠螺母,有为了满足设计要求:j=3,但对于滚珠丝杠螺母副来说螺母是成对使用的,如果设计成两螺母副中一个为一 个循环,另一个为两个循环。这样在预紧的时候两螺母所受的预紧力是一致的,但两边 滚珠所受的力是不一样大小的,使只要一个循环的螺母的一端滚珠与滚道的应力加大, 这样就加快了这一端的失效,所以依然采用两端两个循环的结构。4.3.2滚珠丝杠螺母副的计算1. 滚珠丝杠的主要技术参数:23(1)名义尺寸D0滚珠丝杠的名义直径 D0是指滚珠中心圆得直径。 D0值的选择与滚珠丝杠的承载 能力有关。D0值越大丝杠的承载能力越大。用于数控机床进给驱动中的滚珠丝杠,取D0=20mm100mm。选择D0值应大于丝杠长度 L0的1/351/30。但D0值过大,将造成丝杆自重过大,容易引起弯曲,且增大驱动力矩。因此较大的D0值的丝杠常采用空心结构。(2)基本导程Ph导程Ph应根据设置的脉冲指令要求和负载情况来选择。Ph值大时,允许使用的滚珠直径也大,因而承载能力较强。同时,当名义直径D0确定后, Ph大可使螺纹升角 变大,一般2o,通常取3.5o,这样才能保证高的转动效率。因为 2o时传动效率明显下降。但Ph值过大会造成丝杠部件,特别是螺母加工的困难。如磨削螺母滚道时易发生干涉现象。初选Ph=4mm。(3)滚珠直径d0。滚珠直径d0值可根据制造厂的产品规格查得。在丝杠的导程一定后,滚珠直径过大,会降低丝杠的抗剪切和抗弯曲能力。一般取d0=0.6Ph。初选d0=20mm。(4)滚珠的工作圈数 j和工作滚珠总数 N。根据以往人们的试验结果,在滚珠丝杠的滚珠中,各圈滚珠所承受的载荷是不均匀的。第一圈承受总载荷的 30%45%;而第五圈至第十圈总共才承受载荷的10%。由此可见过多的工作圈数对提高承载能力的作用不大。同时工作圈数越多,分布在滚道内的滚珠个数要增加,容易引起滚珠流动不畅。因此,工作圈数j一般取2.53.5圈,而工作滚珠总数以不大于 150个为宜。但滚珠个数过少,也会造成滚珠和螺纹滚道负荷集中,接触点受力过大等问题。因此在此设计中初选 j=3。(5)列数k。选择滚珠循环方式时必须保证滚珠流动的畅通。为此工作圈数j不应过多。但是 在要求工作圈数多的场合,可采用双列或多列式螺母的结构形式。2. 滚珠丝杠的参数确定:(1)移动部分重量估算:根据外形尺寸及所用材料的密度估算移动部分的重力为:24,33107.8 1010373G = (2.5+0.55+1+0.45+0.4+0.24)则总重为400N。(2)初选公称直径D0=20mm;Ph=4mm;则;接触角为45度;0.63whDPmm(3)基本额定静载荷 Coa。 (4-5)式中 接触角( ) DW钢球直径( mm) z每圈螺纹滚道内的钢珠数量 i螺母的总工作圈数, i=圈数列数 d0 滚动螺旋副的公称直径( mm) rs螺杆滚道的曲率半径 foa基本额定静载荷特性值因取整z30032cos0.106202wsDrad则:(4)基本额定动载荷的计算 (4-6)0.72/31.8( cos)tanacWCf izD2sinoaoawCf izD02020.93wzdD13.8713.8742.16110.16(1)(1)11212 0.551 0.16oasrssfrfr2242.16 3 30 324147.42oaC 0.55rsf2510.410.391219.32()112ScuNrsCff ffCf1sin10(1)3f0.31.3921/3(1)(1)rrfr 1uuhlfp i1.720.41121()112SrNNrsCfrCrf (取整)NrNWrfDsrSWrfD0cosWDrd0WdzD式中 接触角( ) z每圈螺纹滚道内的钢珠数量 DW钢球直径( mm) i螺母的总工作圈数 d0 滚动螺旋副的公称直径( mm) Ph导程( mm) lu有效工作行程( mm)rN 螺母滚道的曲率半径rs螺杆滚道的曲率半径fu工作行程系数frN螺母的适应度frs螺杆的适应度fc额定动载荷特性,与材料的性能、滚道的几何形状有关则: Ca=9670.4查文献 机械设计手册 表15.2-18取d0 =20mm,圈数 列数=14,DW =3综上所述,选用 CMD2005-5的滚珠丝杠副,其主要技术数据见表 4-1:264.3.3 滚珠丝杠螺母副的验算1. 工作力的估算在此检查装置中,其滚珠丝杠在工作中所受的力很小,因为在工作中,测头与被测件的摩擦力以及机器的本身的摩擦力几乎是全部的工作力。 由于采用的是滚珠导轨,其摩擦系数为0.0030.005。根据估算得知移动部分的重量约为400N,取摩擦系数u=0.005,则f=u N =0.005*400=2N,滚珠导轨的预紧力所形成的工作力估为1N,则总的工作力为 3N。4-1 滚珠丝杠技术参数表主要尺寸符号计算公式与结果公称直径D020导程Ph4接触角45钢珠直径d03螺纹滚道曲率半径sr000.51 0.560.551.65srdd螺纹滚道螺纹升角0arctan/3.643hPD螺杆大径000(0.2 0.25)200.219.4dDdd螺杆小径1d10017dDd螺杆接触点直径kd00cos17.88kdDd螺杆牙顶圆角半径ar00(0.1 0.15)0.120.36ardd螺杆偏心距e00.707(/2)0.106serd27螺母螺纹大径D0023DDd螺母螺母螺纹小径1D100()20.6DDDd滚珠丝杠的支承有三种主要形式:(1)一端定,一端自由的支承配置方式,通常用于短丝杠和垂直进给丝杠;(2)一端固定,一端浮动的方式,通常用于较长的卧式安装丝杠。(3)两端固定方式,常用于长丝杠或高转速、高刚度、高精度的丝杠,这种配置方式可对丝杠进行预拉伸。由于此装置是精度较高的检测装置,选择第三种的支承方式。滚珠丝杠常用的滚动轴承有以下两类:(1)接触角为60的角接触球轴承,这是目前国内外广泛采用的滚珠丝杠轴承,这种轴承可组合配置。 (2)刚度验算滚珠丝杠工作负载 P一起的导程L0的变化量 式中A丝杠内径处的截面积( m2) ;E弹性模量,对于钢, E=2102(GPa) ;L0导程( mm) 。因为轴向所受牵引力最大,故应用轴向的参数P为工作力,经估算其值为 3NL0=Ph=4mm62200 10 (/)EN cm223.14(17/2)227.0AR则0pLLEA 1161 48.81 10200 10227.0L 28导程总误差为:11300=8.81 106.61/4hLLm mP 查文献 机械设计手册 表15.2-26,所选足满足设计要求。4.4变速机构中 齿轮的设计 因步进电机的步距角 b=0.9,滚珠丝杠螺距 Ph=4mm,要实现脉冲当量p=0.005mm/step。在传动系统中应加一对齿轮降速传动,齿轮传动比为:=Z1/Z2=0.9pPh/360=2选Z1 =25,Z2=50。4.4.1 齿轮参数计算1.确定齿轮及有关尺寸由于此齿轮为精密测量设备上的传动齿轮,其转速不高但要求传动准确,故选用5级精度,小齿轮材料用 40Cr(调质) ,硬度为280HBS,大齿轮材料用45钢(调质) ,硬度为240HBS,两者材料硬度差 40HBS。小齿轮 齿数Z1=25,大齿轮 齿数Z2=Z1=225=50。 2.按齿面强度设计计算,由设计公式 1)确定公式内的各计算数值(1)选载荷系数K =1.3 (2)计算小齿轮的转矩 T1=95.5105 5.5/960Nmm=5.47104 Nmm(3)查文献 机械设计 表10-7选取齿宽系数 =0.4(4)查文献 机械设计 表10-6查得材料的弹性影响系数 ZE=189.8MPa1/2(5)查文献 机械设计 图10-21d按齿面 硬度查得小齿轮的接触疲劳强度极限,大齿轮按照接触疲劳强度极限 213112.32()EtdHKTZddEZlim1600HMPalim2550HMPa29(6)由公式计算应力循环次数N1=60n1jLh=609601(2830015)=4.147109N2= N1/=4.147109/2=2.074109(7)查文献 机械设计 图10-19查的接触疲劳寿命系数 =0.90;(8)计算接触疲劳许用应力取失效概率为1%,安全系数S=1,由式 2)计算(1)试计算小齿轮分度圆直径 ,代入中较小的值 1tdH(2)计算圆周速度v(3)计算齿宽10.4 76.02430.41dtbdmmmm(4)计算齿宽与齿高之比 b/h,模数齿高 2.252.25 3.046.84hmmmmm/76.024/6.8411.11b h 213142312.32()1.3 5.47 102 1 189.82.32()76.024mm0.42522.5tEtdHK TZdmm1176.024 9603.82/60 100060 1000td nm s1110.9 600540HNHLimHKMPaMPaS2220.95 550522.5HNHLimHKMPaMPaS1HNK20.95HNK11/76.024/253.04ttmdzmmmm30(5)计算载荷系数根据v=3.82m/s,5级精度, 查文献机械设计 图10-8查得动载系数齿轮,假设 ,/100/AtK F bN mm由表10-3查得:1HFKK查文献 机械设计 表10-2查得使用系数;1AK 查文献 机械设计 表10-4查得5级精度、小齿轮相对支承非对称布置时,将数据代入后得 2231.050.18(1 0.6 0.4 ) 0.40.23 1030.411.089hK由b/h=11.11, 1.089HK查文献 机械设计 图10-13的;故载荷系数 1.08fK (4-7) (6)按实际的载荷系数校正所算得的分度圆直径,由式(7)计算模数m 11/72.83/252.91mdzmmmm取整 m=3。3.按齿根弯曲强度设计由文献机械设计 式(10-5)得弯曲强度设计公式为: 2231.050.18(1 0.6)0.23 10hddKb1.05;vK 3311/76.0241.143/1.372.83ttddK Kmm1 1.05 1 1.0891.143AvhFKK K KK 13212()FaSadFY YKTmz31 1)确定公式内的各计算数值。(1)由文献机械设计 图10-20c查得小齿轮的弯曲疲劳强度极限;1500FEMPa大齿轮的弯曲疲劳强度极限;2380FEMPa(2)由文献机械设计 图10-18查得弯曲疲劳寿命系数,;10.85FNKFN2K0.88(3)计算弯曲疲劳许用应力取弯曲疲劳安全系数 S=1.4,由查文献机械设计 式(10-12)得 (4)计算载荷系数KAVFFK=K K KK1 1.05 1 1.081.134 (5)查得齿形系数由文献机械设计 表10-5查得;。12.62FaY22.32FaY(6)由文献机械设计 表10-5查得;11.59SaY21.70SaY(7)计算大、小齿轮的 并加以比较 大齿轮的数值大。2222.32 1.700.01651238.86FasaFYY1112.62 1.590.01342303.57FasaFYY2220.88 380238.861.4FNFEFKMPaS1!10.85 500303.571.4FNFEFKMPaSFasaFY Y322)设计计算对此计算结果,由齿面接触疲劳强度计算的模数m大于由齿根弯曲疲劳强度计算的模数,由于齿轮模数 ,得大小主要取决于弯曲强度所决定的承载能力,而齿面接触疲劳强度所决定的承载能力,仅与齿轮直径有关,可取由弯曲强度算得的模数2.016,并就近圆整为标准值 m=2.5mm。按接触疲劳 算得的分度圆直径,算出小 齿轮172.83dmm齿数 取整1172.8329.12.5dzm130z 212 3060zz4.几何尺寸计算1) z1 =30,z2=60计算分度圆直径为, 1130 2.575.0dz mmmmm。2260 2.5150.0dz mmmmm2)计算中心距a=(d2+d1)/2=(75+150)/2mm= 112.5mm3)计算齿轮宽度10.4 7530dbdmm取B2=30mm,B1=32mm5.验算41122 5.47 101458.775.0tTFNNd413322122 1.134 5.47 10 N.mm()0.016512.0160.4 25FaSadFY YKTmmmz33合适。1 1458.7/19.45/100/,75AtK FN mmN mmN mmb34结论本设计的主要任务是对零前角阿基米德齿轮滚刀的齿形误差进行检测。设计的开始 要对设计课题进行分析 ,由分析得出 多种设计方案。然后对各设计方案进行比较 选择,确定设计方案 。根据设计方案分析设计的 主要内容与难点问题 。最后对设计的主要内容与难点问题实施有计划的完成。本设计的 难点问题 是:(1)检测装置的横向和纵向运动的实现;(2)检测装置精度如何保证;(3)被测 滚刀定位夹紧 装置的确定 。解决问题所采取的措施 :检测装置的横向和纵向 运动采用相同型号的步进电机驱动滚珠丝杠旋转,滚珠丝杠通过丝杠螺母把旋转运动转换成直线运动并带动工作台工作。本设计要求精度 很高,导轨选用滚动导轨 。选用一定锥度的心轴对滚刀 同时进行定位夹紧。本设计的主要内容是对横纵向进给装置中电机进行选择,对滚珠丝杠,滚动导轨,变速齿轮等进行设计计算。35致谢本文主要阐述了 阿基米德齿轮滚刀检测装置设计。通过这次设计使我对齿轮加工过程产生了浓厚的兴趣,同时,受我主修专业的影响,我已经习惯于设计带来的一系列机遇与挑战 。本篇论文虽然凝聚着自己的汗水,但却不是个人智慧的产品,没有导师的指引和赠予,没有父母和朋友的帮助和支持,我在大学的学术成长肯定会大打折扣。当我打完毕业论文的最后一个字符,涌上心头的不是长途跋涉后抵达终点的欣喜,而是源自心底的诚挚谢意。我首先要感谢我的指导老 师张文生 老师,对我的构思以及论文的内容不厌其烦 的进行多次指导和悉心指点,使我在完成论文的同时也深受启发和教育 。其次我要感谢带我们到东安集团参观齿轮检测装置的卢老师、齿轮检测实验室的 刘老师,以及和我一起研究设计方案的同学们。再次由衷感谢答辩组的各位老师对学生的指导和教诲,我也在努力的积蓄着力量,尽自己的微薄之力回报母校的培育之情,争取使自己的人生对社会产生些许积极的价值!36参考文献1 孙桓,陈作模 .机械原理 .第六版 .高等教育出版社 .20012 李柱,徐振高、蒋向前 .互换性与测量技术 .高等教育出版社 .20043 濮良贵 ,纪名刚 .机械设计 .第七版 .高等教育出版社 .20014 西安交通大学,乐兑谦 .金属切削刀具 .第二版 .机械工业出版社 .20045 杜君文 .机械制造技术装备及设计 .天津大学出版社 .20046 张萍.齿轮滚刀齿形检测技术探析 .北京工业职业技术学院学报 .2005,47 张树森,王成俊 ,隋新,方森松 .齿轮滚刀重磨齿形误差的研究.阜新矿业学院学报 .1994,78 傅耀先 .滚齿时必然产生的几种误差 .工具技术 .2000,第29卷:6-109 赵仲生 ,赵一丁 ,林其骏 ,方素平 .齿轮滚刀测量机数控系统的开发.机械科学与技术 .1995年第1期10 金光哲 .3203型齿形齿向测量仪 .测量与设备 .2002,第11卷:32-3311 王建华 .滚刀齿侧面整体误差及测量 .西安工业学院学报 .1995,312 任凤国 ,杨春生 .齿轮滚刀齿形检测方法分析 .煤矿机械 .2001年第10期13 卢春霞 .偏心齿轮齿形误差的测量 .西安工业学院学报 .1999,第19卷:71-7414 经挺度 .汽车工业中齿轮精度的检测及其测量仪器.工具技术 .2003,第28卷:29-3215 杨新建 .航空发动机渐开线圆柱齿轮工艺设计.西北工业大学硕士论文 .2000,27-4416 刘成雁 .圆柱齿轮加工误差分析及改进途径.建设机械技术与管理 .2004,第5期:29-3017 吴祖育,秦鹏飞 .数控机床 .第三版 .上海科技出版社 .2000,13718 邓星钟 .电机传动控制 .第三版 .华中科技大学出版社 .2000,619 机械设计手册 .新版.机械工业出版社 .2005.1020 实用机床手册 .辽宁科学技术出版社 .1999:1页-1262页21 史恩秀,田晓虹,李永堂 .渐开线圆柱齿轮齿形误差的测量与计算.太原重型机械学院院报 .2000,322 杨 昆.用CNC齿轮测量中心实现滚刀误差项目的连续测量.西安工业学院报 .38附录1绝热高速切削有限元模型摘要二维正交切削过程的有限元模型正在发展。仿真是使用标准的有限元软件 结合一个特殊的电动机 ,这种电动机是 能够以网捕捉 的形式用有规律的 四边形和 三角形 在剪切区域完整的捕捉事物。重现事物和确保数据收敛的这种技术已经寻找到了 。分割碎片有序排列和分割过程还在研究过程中。令人特别关注的是剪裂带 产生的问题 。弹性性能和切割速度 的影响也正在 讨论。 Elsevier公司2002科技有限公司保留所有权利 。 关键词:加工; 有限元 ; 格; 芯片分割 ;绝热剪切带 1、言 钛合金Ti6Al4V被广泛应用于航空航天及其他工业应用。这些合金大部份 是应用 于机械加工 。 因此设计 具有更好的可加工性钛合金是一个值得研究的目的。为了达到这一目的 ,找出严重影响 材料可加工参数 是非常必要的 。这项工作可以利用有限元计算机模拟 的参数研究 方法来完成 。一旦这最有前途的设计 方法被肯定 ,实现合金改用的最后的一步材料设计过程就完成了。这种方式类似于标准的 CAE生产周期 ,只有仅有少量几个 原型被建立 。创造一个金属切削过程 的可靠的计算机模型在这个过程中是一个关键步骤。在本文中,我们在一些细节 描述了 这种模型 。它使用标准的有限元软件 来计算,从而保证可移植性和灵活性 。随着啮合算法 的要求迫切 ,特别预处理器已经研制成功 ,这个特别的处理器是用C+编程,且可能应用于不同平台 。 本文安排如下 ;第2部分在 对模型要求的一个简短说明 之后, 第3部分对 有限元模型进行详细介绍。 第4简述了一 些模型 的加工 成果,重点放在细节的切屑形成过程。第5总结工作 ,并指出今后的研究目标 。 2、问题 在金属切削过程中 ,材料被 切割工具从工件表面 切除,碎屑形成 。 这个问题涉及塑性大变形 ,随着刀具和工件 、工具和 碎屑之间的 摩擦产生大量的热量 。在刀具前端 工39件材料 的分离 也已经被模拟 。随着材料参数 的影响对材料设计的考虑比对加工过程本身更重要。这个切削过程 的模拟就是 指正交切削 。这个过程是 用二维模拟 的,这大大减少了计算机所需要的计算时间。更进一步简化是做 非常严格的 假设的工具。在仿真 中摩擦与热流 进入工具已经被忽略 ,但是 可以很容易被包括在内 。 这种忽略的原因是 ,有必要尽可能简化切削过程 ,像下文将作解释 那样, 透视其背后的机制 。 另外,毫无塞尔马辐射从表面上的 碎屑产生,在 材料边界 也没有的热传导。综上所述 ,高速切削是一个非线性问题 。它已经被 一个完全热力耦合有限元模型模拟。 因此,编制了有限元法处理金属切削加工时的划伤问题就成为 一个艰巨的任务 ,利用商业有限元软件是一个有吸引力的替代方案。 现代有限元软件可以在原则处理这类强非线性问题 。在我们的研究 中,我们决定用ABAQUS中/标准程式系统 ,这种系统 允许定义复杂的接触状况 ,尽量避免定义材料属性, 在多方面 保证程序 可定制的 ,包括由 用户自定义子程序 。我们假定 以下大部分 的方法可以应用于 同样大的有限元 包。 由于使用的标准化软件 ,方程公式(有限元法 ,热耦合 ,一体化计划 ,等)可以在别的 非常详 细的资料中 找到3。金属切削过程中许多有限元模拟所用明确的方法(例如见 17 )都能被演示。这些公式方法都是有保证的。 (概述了切削过程 中有有限元 能够被在 16中好到 )。尽管如此 ,决定用一个隐码 . 在模拟 过程中汇总被 检查,但迭代过程不再保证衔接 。利用ABAQUS /标准内含编码有一个好处 ,实行模拟 过程中允许 用户在很大的范围内 灵活的自定义子 程序。 这种套路 ,可以用来执行复杂的材料分离准则。 此外,如果本地网 有细化的需要 ,隐码有较好的标度行为 。如果狭窄剪切带形式 , 命令执行的 单元尺寸为1镑或不足1镑是必要的 (见第4.2 节)优势,在CPU 使用时间有明确的算法 ,将大大降低 。如果摩擦 的影响较大 ,一个明确的方法可能是上 好的,然而, 并非如此 。另一方面 ,明确方法往 往需要改变一些物理参数 ,如密度或工具的速度 ,或用人工粘性 。 我们认为 , 如果衔 接能够达到 ,没有任何理由去考虑的一个隐模拟不亚于一个明确的。 也不同于许多其他的模拟 ,我们充分利用综合阶四边形 ,它有优于三角元素更好的收敛性能 . 这个问题的 进一步讨论在第 3.3节。 当正交 切削时, 钛合金形式分割 碎屑 (见图 9 )。金属切削过程中任何详细 的模拟都必须能够 借此分割考虑 。碎屑分割背后的机制仍然没有完全弄懂12,15,25,26。显然,所谓的绝热剪切 在分割过程 起了突出的作用 : 剪切带材料热软化 导致在这个区域产生变形。在软化和变形之间的反馈 引起狭长区域附加巨大 变形, 而周围的 材料只产生微小变形。然而, 不知道绝热剪切带是否 是由裂缝延伸到材料中引起的成的,这在 25是作为假设 。如果这 是正确的, 应力集中在裂纹尖端诱 引起剪切带形 变(见例如 5 )。 40在这里通过对 该模型描述,我们假定 碎屑分割是 由纯绝热剪切 ,不是裂缝引起的。 很显然, 剪切带材料点 的有效塑性流动曲线 必须表明最大值。 我们选用一个 使温流动曲线出现最大值曲线流场 ,详细解释见4.1节。 如果分割 碎屑形式,集中应力 导致了 碎屑(近似)连续变形 。必须采取措施 ,以避免有限元网格 因扭曲太大而 变形,尤其是在 用四边形 元素仿真的 的过程中。综上所述 ,模拟需满足下列要求 : 尽可能定期使用四边形 ,避免极端网格扭曲 ;剪切带 内高密度网 格; 碎屑连续变形 (分割); 隐式算法收敛 ; 为得到 可移植性和灵活性使用标准软件。在金属切削模拟 ,为自动形成网格算法的选用 是固定的,如用 拉格朗日方 算法, 元素扭曲变大 ,尤其是 分割碎屑 形式。频繁重复分割以避免 分子扭曲 太大。在材料移出的剪切带它也可以用来制造 精确网格(见插图6)。 然而,标准网 格发电机是不能处理复杂的任务。因此,预处理程序 已经编辑了能够分割曲率很大的被用 四边形 剪切生成的区域程序。 剪切带 的位置是用几何判据 和网格细化自动 决定的。 预处理程序将 在下一节描述 。随后,对网格生成过程和建模的分割 的详细内容作解释 。3.有限元模型3.1网发电 的原理过去的 预处理程序 (被称为pre+ )都是用 标准数据库在C+中写的, 因此,可以 移植到不同的平台 。 预处理程序被 用来计算几何参数数据 ,使模型参数 轻松改变。它适用于二维三维空间中 各种各样的问题 。生成四边形最简单的办法是 划分组件的物理区域 ,组件是被 四条线 和一个映射单 位正方形 限制的。 单位正方形 有规律的 啮合可以映射回 用等角投影的 该地区本身 。细节 的详细叙述 见23,24 。如果我们在 真实空间内用 (x,y),在平面内用( ,)定义 坐标,一般曲线坐标系可以 通过解 拉普拉斯方程 来定义 (1)0xxyy (2)0xxyy41这里的表示,等等。 这个方 程系统的物理解释 :当两个对立 边携带 不同的电xx22x压,坐标协调电场区域的等 势线。 把坐标( , )作为独立变数 ,这当然是很容易 求解的 方程。在这种情况下方 程已被颠倒过来 ,求解 (3)222220xyxx xy yxxyx (4)222220xyyx xy yyxyy这是一个半椭圆形的线性方程组求解,可以解决使用标准方法 。啮合算法通常是 用来制造网在一个物理地区 ,是经过了一个有限元计算 的结果 ,因为它 被用来自动 生成网格的过程 。 因此,界限被 计算步骤 定义, 因此已经离散 。求解方程, 定期矩形网使 用的网格大小的选择应小于最小距离,使等量的旧与新网 相同。 由于不规则形状的区域解点数目已是一个相当大的数据,谨慎 选择算法是有 优势的。我们已经 制定了一个多重算法 ,详细介绍见 勃兰特 7。 这种算法的优点是快速 ,稳定,而且也给出一个截断误差 的估计。这种计算方法可以起到数值误差是可比的截断误差。 由于方程是非线性的 ,只能用 近似格式 ( FAS )的方法来进行 。多重技术依赖的事实标准松弛方法 (如高斯 -赛德尔 )非常有效地减少振荡解决部分误差,而畅顺 ,大部份波长不影响不大 。因此,我们经过几个步骤放宽任何涉及方程的误差可以代表以及对粗网少点。放松对这个粗格再次降低小波长组成,其中, 现在有一个较大的绝对波长为电网是粗糙。因此,递归计划是用在错误的 ,是有效降低对所有尺度 。 这种算法是一 个标准的工具 ,用于解决椭圆型方程使读者可参考文献进一步的详细内容 20。它只需 约一分钟,一个标准的工作站 ,即使格数点约 为250 000只要界限的区域不是太强烈 弯曲。插图1( a )显示坐标系 在一个 简单的区域 被用描述算法创建。42附录2A finite element model of high speed metal cutting with adiabatic shearingAbstract A finite element model of a two-dimensional orthogonal cutting process is developed. The simulation uses standard finite element software together with a special mesh generator that is able to mesh the chip completely with regular quadrilateral elements and a strong mesh refinement in the shear zone for continuous and segmented chips. The techniques of remeshing and to ensure convergence of the implicit calculation is described. Results for the formation of segmented chips are presented and the segmentation process is studied. Of special interest is the occurrence of split shear bands. The influence of the elastic properties and of the cutting speed is also discussed.Keywords: Machining; Finite elements; Remeshing; Chip segmentation; Adiabatic shear bands 1. Introduction Titanium alloys like Ti6Al4V are widely used in aerospace and other industrial applications. A large fraction of the production costs for components made of these alloys is due to machining. The design of titanium alloys with better machinability is therefore a worthwhile research aim. To achieve this, it is necessary to identify the important material parameters that critically influence the machinability of the material. This can be done by parameter studies using finite element computer simulations. Once the most promising design avenues are determined, the actual alloy modification can be done, which is thus only the final step of the material design process. This approach is similar to the standard CAE production cycle, where only a few prototypes are built. 43* Corresponding author. E-mail addresses: martin.baekertu-bs.de (M. Baker), j.roeslertu-bs.de (J. Rosler), c.siemerstu-bs.de (C. Siemers). 1 Work supported by Deutsche Forschungsgemeinschaft. Creating a reliable computer model of the metal cutting process is the first and crucial step in this process. In this paper, we describe such a model in some detail. It uses standard finite element software for the calculations, thus ensuring portability and flexibility. As the requirements on themeshing algorithm are quite strong, a special preprocessor has been developed, which is programmed in Ctt and is thus also portable to different platforms. The paper is organized as follows: after a short description of the requirements on the model in Section 2, the details of the finite element model are given in Section 3. Some results produced with the model are shown in Section 4, focussing on the details of the chip formation process. Section 5 summarizes the work and points out future research aims. 2. The problem In the metal cutting process material is removed from the surface of the workpiece by a cutting tool and a chip is formed. The problem involves large plastic deformations which generate a considerable amount of heat, as does the friction between tool and workpiece and also between tool and chip. The separation of workpiece material in front of the tool also has to be modeled. As the influence of the material parameters is more important for material design considerations than are the details of the process itself, the cutting process simulated here is that of orthogonal cutting. The process is simulated as two-dimensional, which strongly reduces the computer time needed for the calculation. A further simplification is done by assuming the tool to be perfectly rigid. Friction and heat flow into the tool have been neglected so far in the simulations, but can easily be included. The reason for this omission is that it is necessary to simplify the cutting process as much as possible to gain insights into the underlying mechanisms as will be explained below. Also, there is no thermal radiation from the free surface of the chip and no heat transfer at the boundary of the material is allowed. 44Rapid machining is a strongly non-linear problem due to the effects described above and it has to be simulated using a fully coupled thermomechanical finite element model. It is therefore a formidable task to develop a finite element code to deal with the metal cutting problem from scratch, so that the use of commercial FE software is an attractive alternative. Modern finite element software can in principle handle such strongly non-linear problems. For our studies we have decided to use the ABAQUS/Standard program system, which allows the definition of complex contact conditions, leaves many possibilities to define material behaviour, and can be customized in many regards by including user-defined subroutines. We suppose that most of the methods described below would work with any similarly powerful FE package. Due to the use of standardized software, the formulation of the equations (finite element formulation,thermomechanical coupling, integration scheme, etc.) can be found in great detail elsewhere 3. Many finite element simulations of the metal cutting process are performed using the explicit method (see for example 17), which is guaranteed to converge. (An overview over finite element simulations of the cutting process can be found in 16.) Nevertheless, we have decided to use an implicit code. Here convergence is checked during the simulation, but the iterative solution process is no longer guaranteed to converge. One advantage of using the implicit code ABAQUS/Standard is that this allows a great range of flexible user-defined subroutines to be introduced in the simulation. Such routines can be used to implement complicated material separation criteria. In addition to that, the implicit code has a better scaling behavior if local mesh refinement is needed. If narrow shear bands form, element sizes of the order of 1 lm or less are necessary (see Section 4.2) and the advantage in CPU time of using an explicit algorithm will strongly diminish. An explicit method is probably superior if frictional effects are large, which is, however, not the case here. On the other hand, explicit methods often need to change some physical parameters like density or tool velocity, or have to use artificial viscosity. In our opinion, there is no reason to consider an implicit simulation inferior to an explicit one, if convergence can be achieved. Also differently from many other simulations, we use fully integrated first-order quadrilateral elements, which have better convergence properties than triangular elements. This is discussed further in Section 3.3. 45Titanium alloys form segmented chips when cut orthogonally (see Fig. 9). Any detailed simulation of the metal cutting process must be able to take this segmentation into account. The mechanisms behind chip segmentation are still not completely understood 12,15, 25,26. It is clear that so-called adiabatic shearing plays a prominent role in the segmentation process: Thermal softening of the material in the shear zone leads to an increased deformation in this zone, which produces heat and leads to further softening. This positive feedback between softening and deformation causes a narrow band of extremely strong deformation, while the surrounding material is only slightly deformed. It is, however, not known whether the adiabatic shear bands are caused by cracks growing into the material, as assumed in 25. If this is true, the stress concentration at the crack tip can then induce the formation of the shear band (see e.g. 5). For the model described here, we assume that chip segmentation is caused by pure adiabatic shearing, without cracks occurring. It is quite clear that the effective plastic flow curve of a material point in the shear band must show a maximum for this mechanism to hold. We have used a flow curve field where even the isothermal flow curves show a maximum. This is further detailed in Section 4.1. If segmented chips form, the shear concentration leads to a (nearly) discontinuous deformation of the chip. Measures have to be taken to ensure that the finite element mesh is not too much distorted due to this deformation, especially in a simulation using quadrilateral elements. To summarize, the simulation has to meet the following requirements: . use of quadrilateral elements, as regular as possible, avoiding extremely distorted meshes; . high mesh density in the shear zone; . discontinuous deformation (segmentation) of the chip; . convergence of the implicit algorithm; . use of standard software for portability and flexibility. The use of an algorithm for automatic remeshing is mandatory in a simulation of metal cutting, as element distortions become large in a Lagrangian approach, 2 especially if segmented chips form. A frequent remeshing ensures that the elements never become too distorted. It can also be used to create a refined mesh in the shear zone that moves with the material (see Fig. 6). 46However, standard mesh generators are not able to handle the complex tasks involved in this problem without difficulties. Thus a preprocessor has been programmed that can mesh the strongly curved regions created by the cutting process using quadrilaterals. The position of the shear zone is automatically determined using a geometric criterion and the mesh is refined there. The preprocessor is described in the following section. Afterwards, details of the mesh creating process and of the modeling of the segmentation are explained. 3. The finite element model 3.1. Principles of mesh generation The used preprocessor (called Pre+) is written in Ctt using standard class libraries and is thus portable to different platforms. The preprocessor can be used to calculate parametrized geometry data, so that model parameters can easily be changed. It is applicable to a wide range of problems in two and (with some restrictions) in three dimensions. The easiest way of generating quadrilateral elements is to divide the physical region to be meshed into parts that are bounded by four lines and can be mapped onto the unit square. A regular meshing of the unit square can then be mapped back onto the region itself using a co
- 温馨提示:
1: 本站所有资源如无特殊说明,都需要本地电脑安装OFFICE2007和PDF阅读器。图纸软件为CAD,CAXA,PROE,UG,SolidWorks等.压缩文件请下载最新的WinRAR软件解压。
2: 本站的文档不包含任何第三方提供的附件图纸等,如果需要附件,请联系上传者。文件的所有权益归上传用户所有。
3.本站RAR压缩包中若带图纸,网页内容里面会有图纸预览,若没有图纸预览就没有图纸。
4. 未经权益所有人同意不得将文件中的内容挪作商业或盈利用途。
5. 人人文库网仅提供信息存储空间,仅对用户上传内容的表现方式做保护处理,对用户上传分享的文档内容本身不做任何修改或编辑,并不能对任何下载内容负责。
6. 下载文件中如有侵权或不适当内容,请与我们联系,我们立即纠正。
7. 本站不保证下载资源的准确性、安全性和完整性, 同时也不承担用户因使用这些下载资源对自己和他人造成任何形式的伤害或损失。

人人文库网所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
 川公网安备: 51019002004831号
川公网安备: 51019002004831号