生物材料动态力学实验机的研制设计【9张图纸】【优秀】
收藏
资源目录

压缩包内文档预览:
编号:423425
类型:共享资源
大小:9.21MB
格式:RAR
上传时间:2015-04-08
上传人:上***
认证信息
个人认证
高**(实名认证)
江苏
IP属地:江苏
39
积分
- 关 键 词:
-
生物材料
动态力学
实验机
研制设计
图纸
动态力学实验机
- 资源描述:
-
生物材料动态力学实验机的研制设计
37页 15000字数+说明书+外文翻译+9张CAD图纸【详情如下】
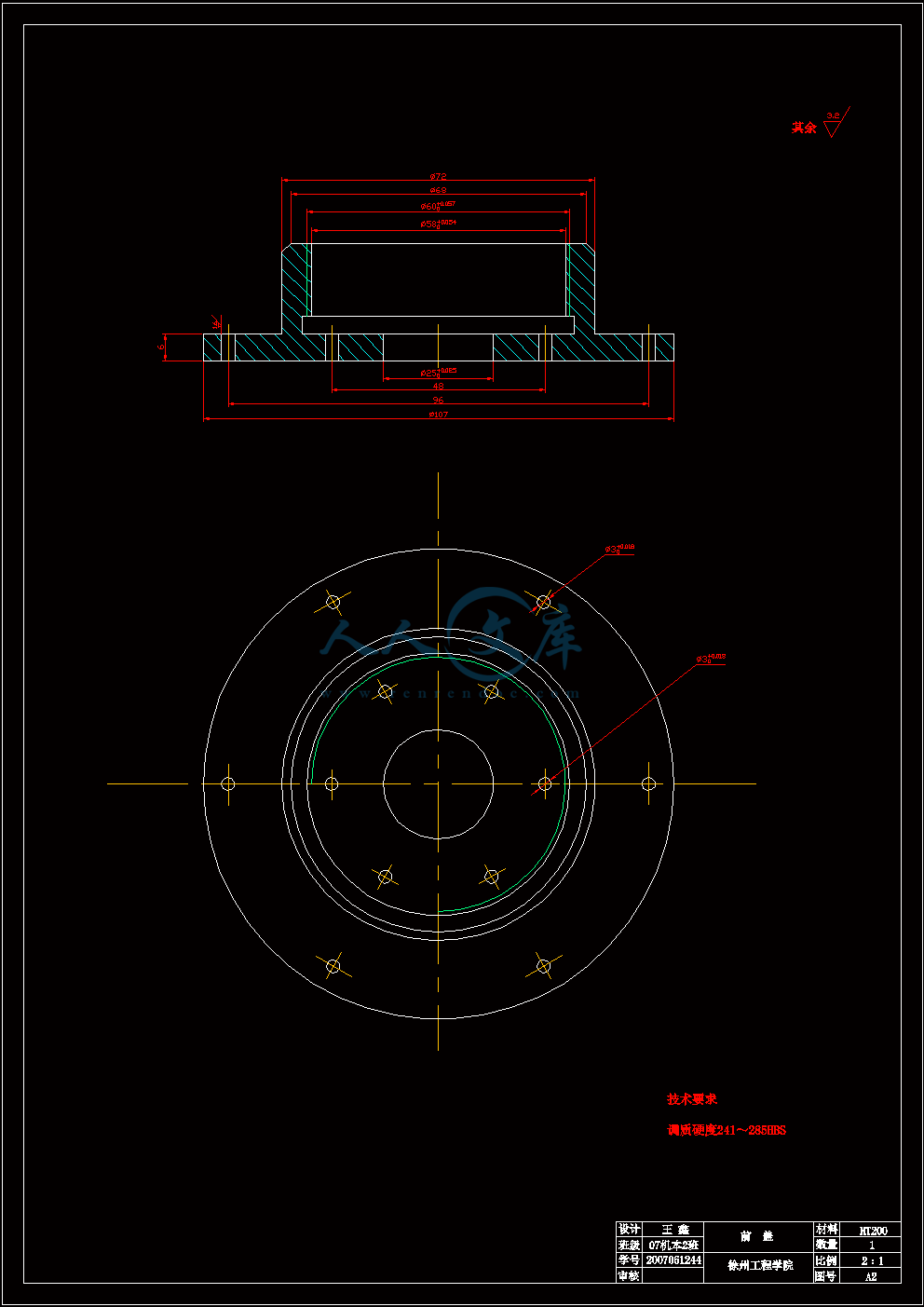
前盖.dwg
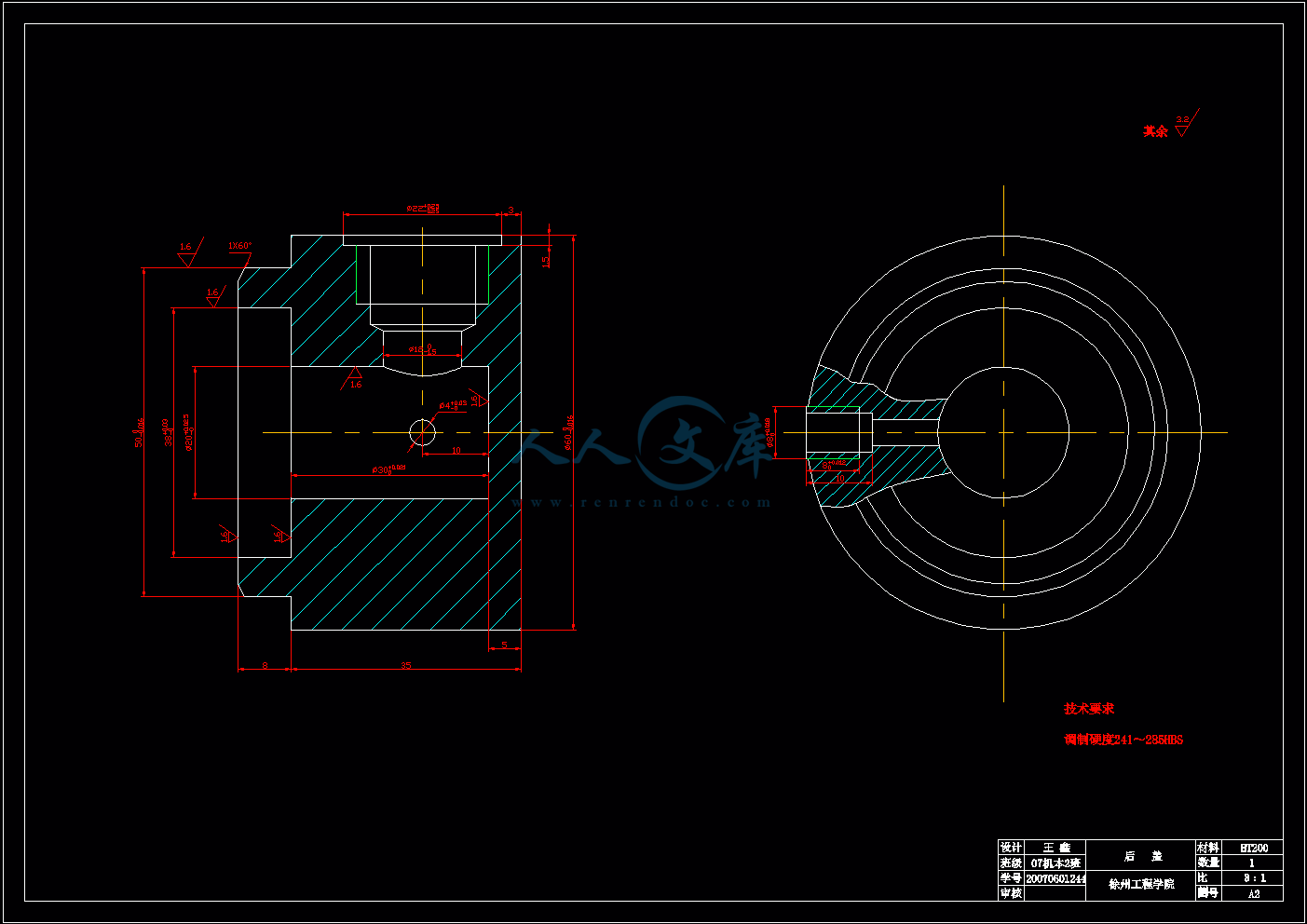
后盖.dwg
外文翻译--液压支架的最优化设计.doc
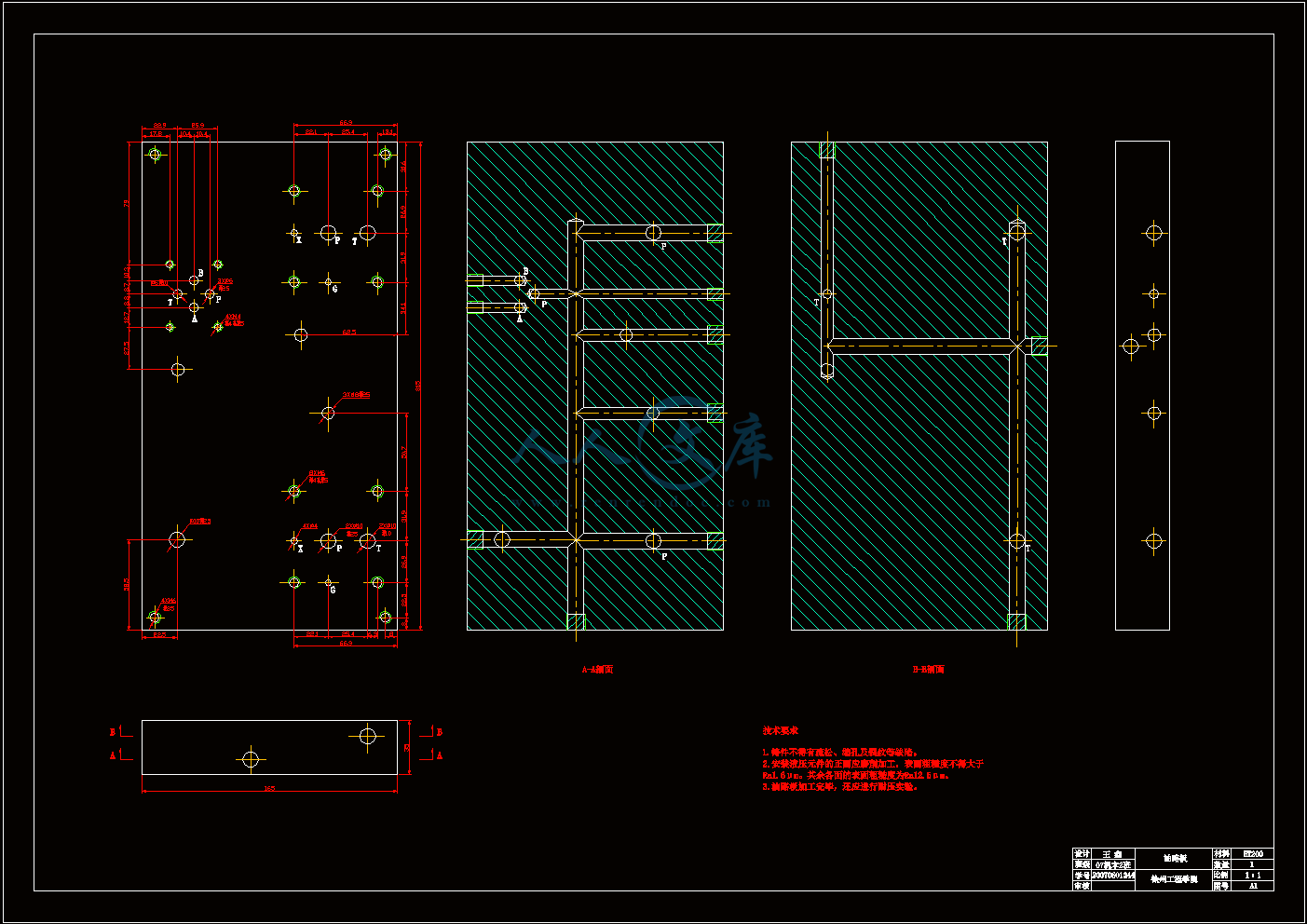
油路板.dwg
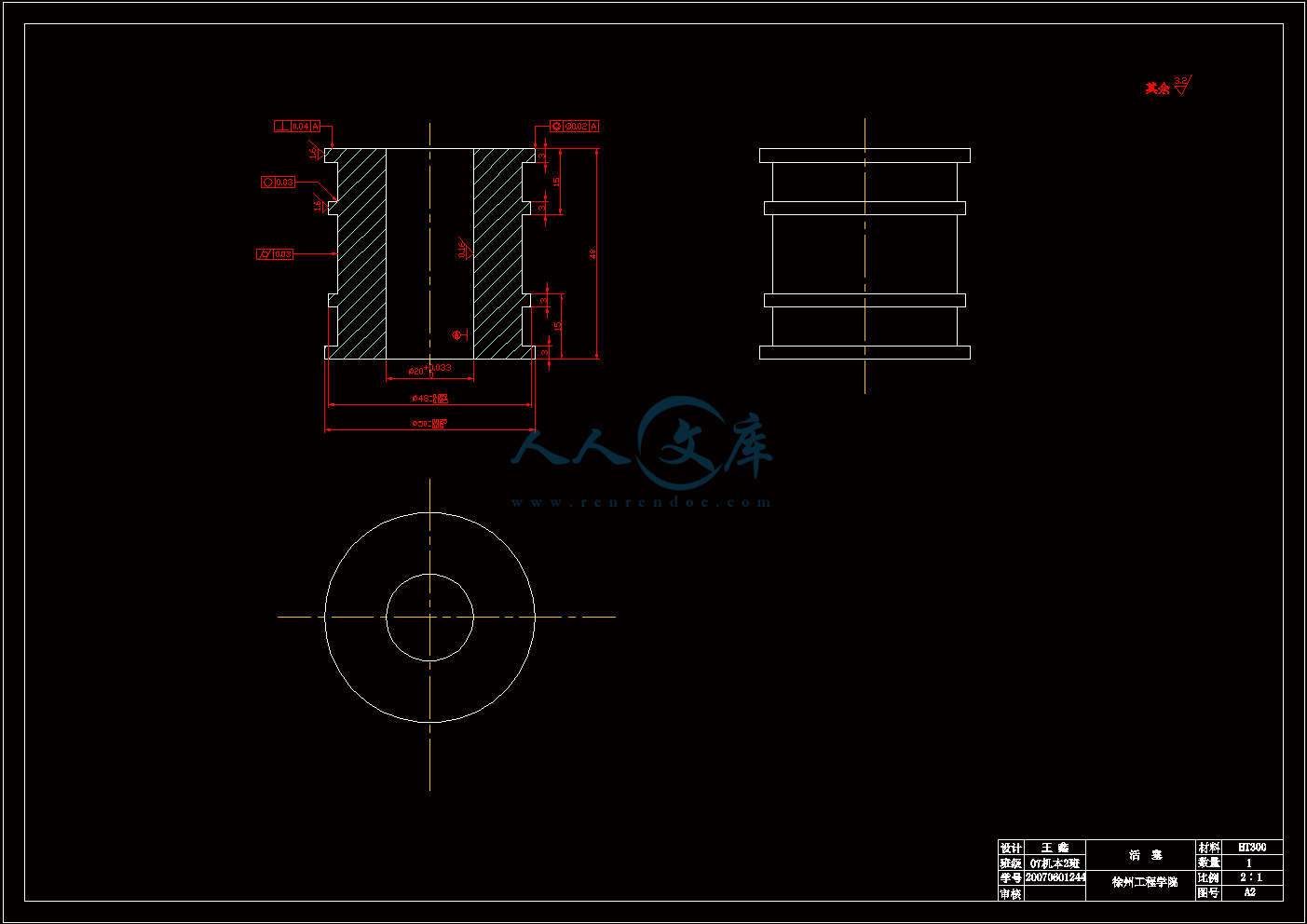
活塞.dwg
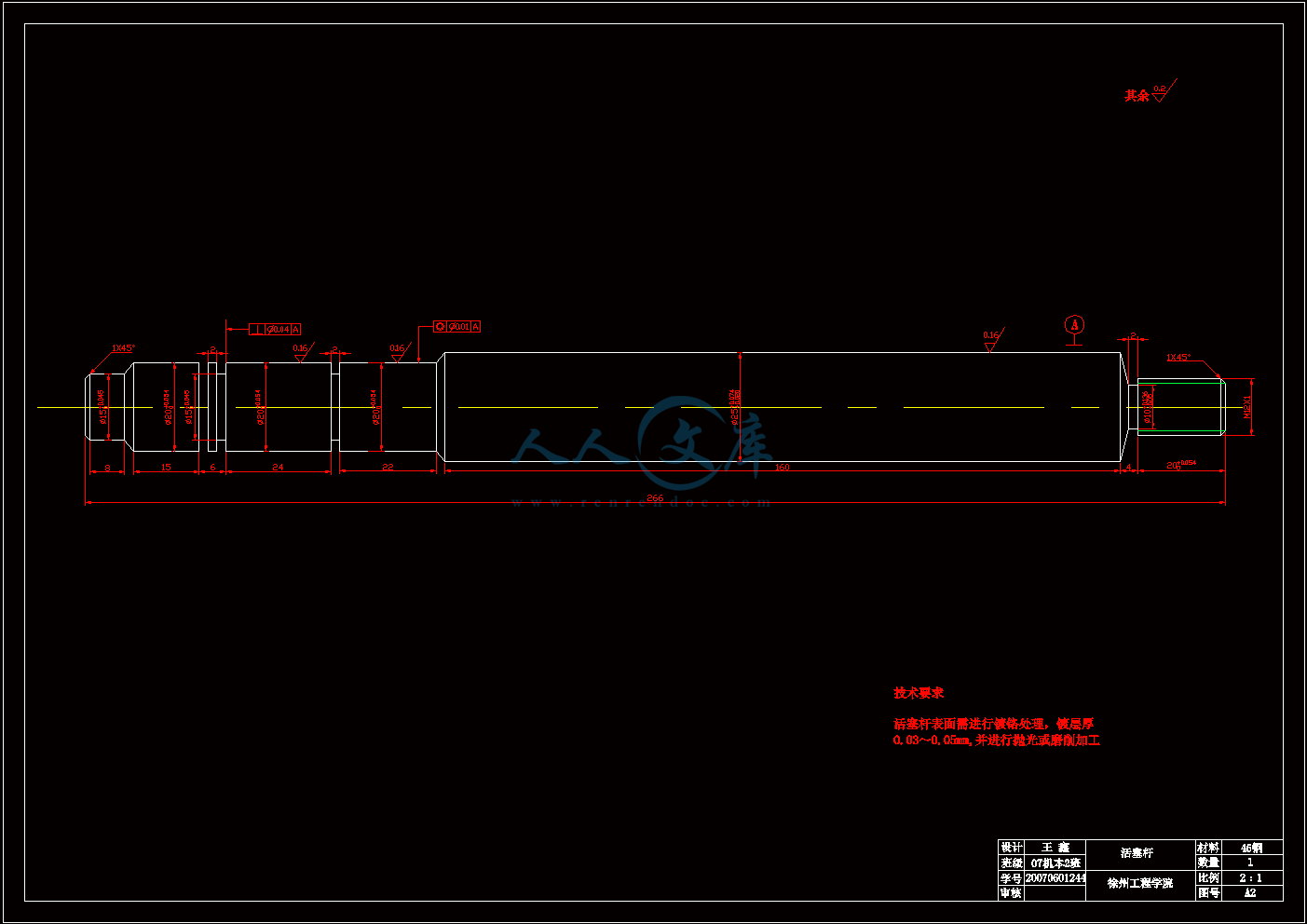
活塞杆.dwg
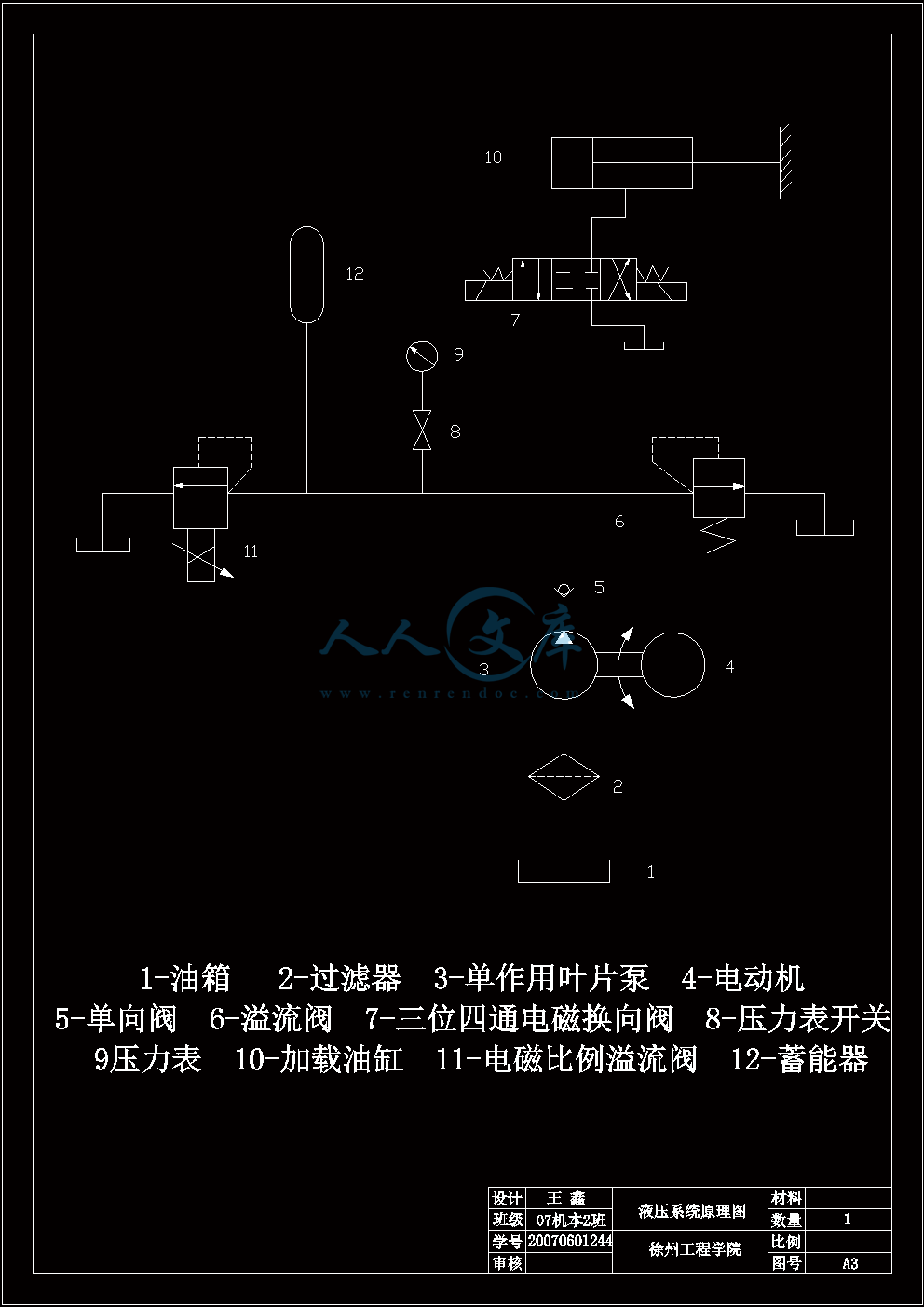
液压原理图.dwg
液压站装配图.dwg
生物材料动态力学实验机的研制设计说明书.doc
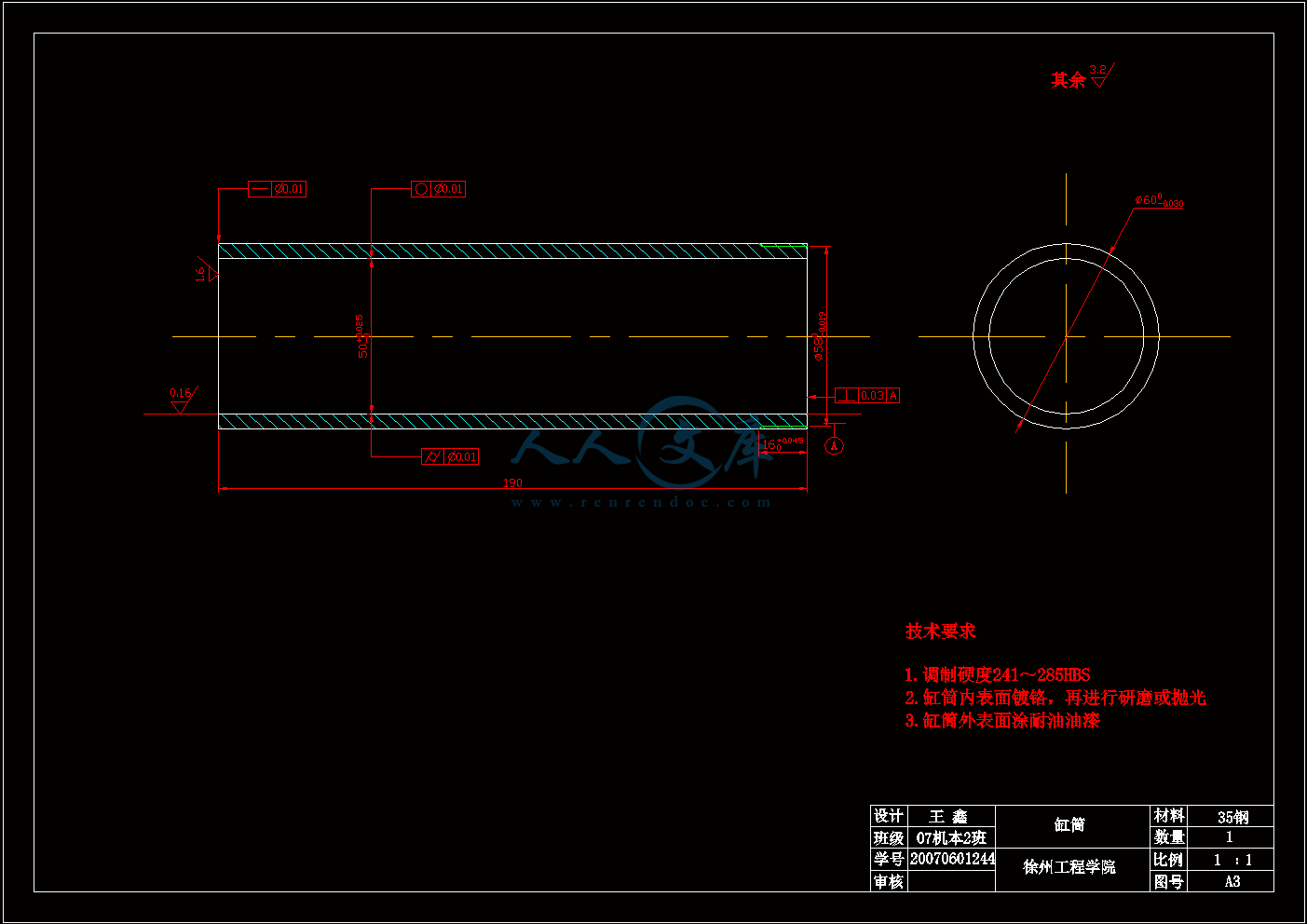
缸筒.dwg
论文.doc
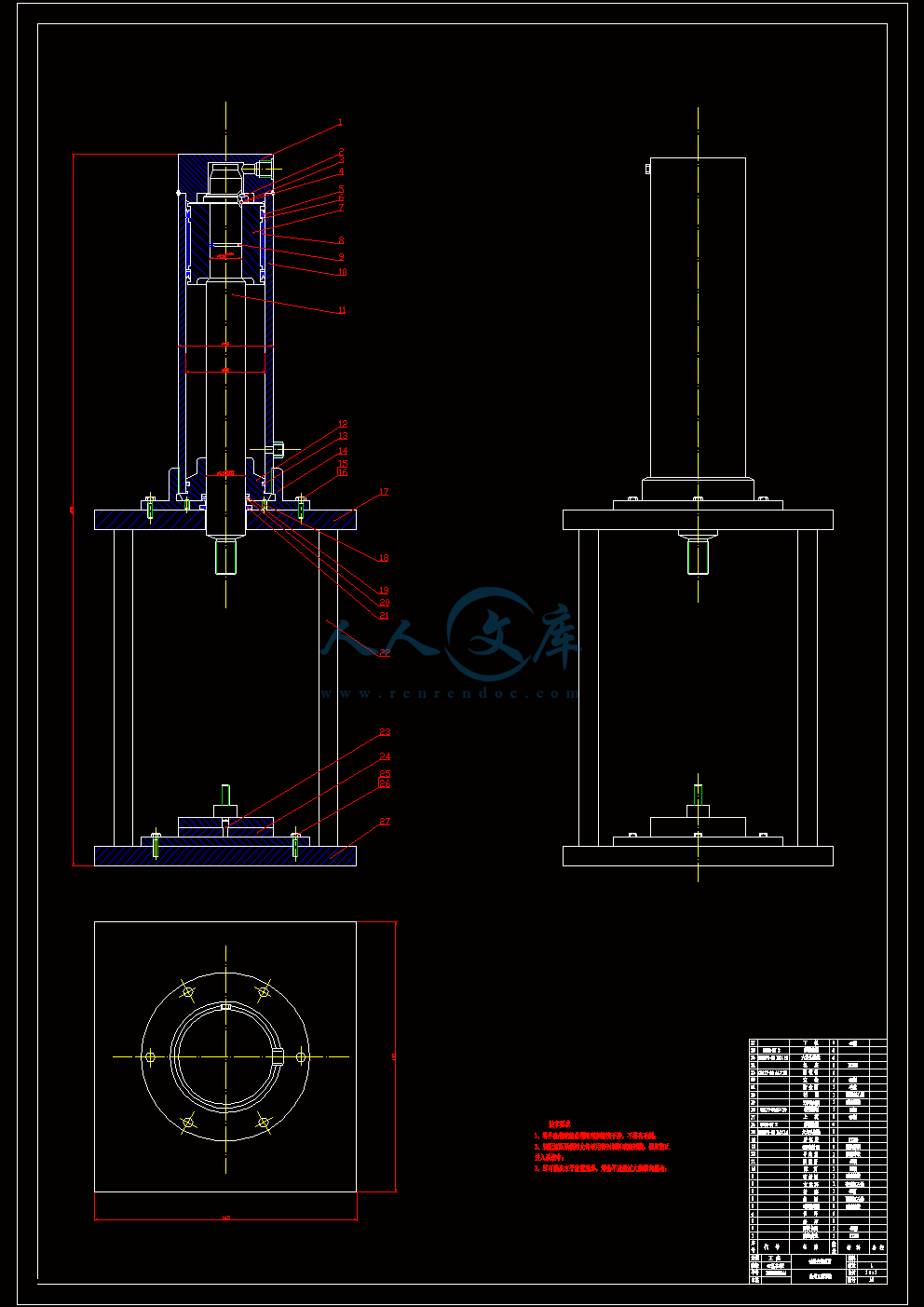
试验台装配图.dwg


目录
摘要I
AbstractII
1 绪论1
1.1 引言1
1.2 人工髋关节模拟试验机的分析与研究1
1.3人工髋关节假体材料的性能要求1
1.4 本课题研究内容拟解决的主要问题2
2 髋关节结构及运动分析3
2.1人体髋关节结构3
2.2 髋关节运动分析3
2.3 人工髋关节结构6
2.4 试验机的工作原理6
3 液压系统设计8
3.1 液压加载系统的设计流程8
3.2 液压加载系统的工作原理8
3.3 液压加载系统的回路设计8
3.4 液压系统的参数计算9
3.4.1液压缸主要参数的确定9
3.4.2 液压泵的性能参数计算11
3.5 液压元件的选择12
3.5.1 控制阀的选择12
3.5.2 辅助元件的选择14
4 液压缸主要零部件设计15
4.1缸筒15
4.1.1 缸筒结构15
4.1.2 缸筒材料15
4.1.3 缸筒计算16
4.2 活塞18
4.2.1 活塞结构18
4.2.2 活塞与活塞杆的连接形式18
4.2.3 活塞的密封18
4.2.4 活塞材料20
4.2.5 活塞尺寸及加工公差20
4.3活塞杆20
4.3.1 活塞杆结构20
4.3.2 活塞杆的材料和技术要求21
4.3.3 活塞杆的计算21
5 液压站的设计23
5.1 液压泵站23
5.2液压泵站的类型选择23
5.3液压油箱及其附件23
5.3.1 油箱的用途与分类23
5.3.2 油箱的构造与设计要点23
5.3.3 油箱的容量及计算24
5.3.4 标准油箱的规格及外形尺寸25
5.4 油路板的设计26
5.4.1 板式集成的结构特征26
5.4.2 油路板的设计要点26
5.4.3 油路板设计说明26
结论30
致谢31
参考文献32
摘要
本课题完成了人工髋关节模拟试验机液压系统及力学试验台的研制。该试验设备主要由机械传动部分、温控系统及液压加载系统组成。试验机液压系统的特性是根据模拟人工髋关节受力特点,可实现交流负载。该液压加载系统主要用于实现关节头试件的前进、后退及载荷的施加。实验台的工作原理是将股骨头和髋臼部件试样按照其正常位置安装于试验台上,通过试验装置使两者之间产生规定的随时间变化的负载。该液压系统及试验台设计时考虑的主要因素是如何实现交流加载特征(交流液压站),使其提供的载荷能在试验室环境中正确模拟人体髋关节的实际受力工况,以使试验机产生的运动形式与人工关节实际使用条件相一致,从而可以准确、可靠地测试人工关节材料的生物摩擦学特性参数,为临床应用提供指导性试验数据。
关键词 人体髋关节;模拟实验;液压加载系统
1 绪论
1.1 引言
人工关节是模拟人体关节制成的植入性假体,以代替病变或损伤的关节并恢复其功能。人工关节的研制、开发是一门跨领域的交叉学科,涉及到材料学、力学、生物学、成型技术和医疗等多门学科的知识,需要多方面的科研人员不断探索。其中,对人工关节生物摩擦学特性的研究由于直接关系到置换关节的使用质量和临床寿命而备受人瞩目。人体关节属于身体活动的连接机构,接触界面间必然发生相对滑动,因此会产生摩擦、磨损和润滑等摩擦学问题。摩擦副结构设计、材料选择、摩擦磨损特性评价以及摩擦过程、磨损机理的研究都需要进行摩擦学试验。由于摩擦磨损测试涉及整个摩擦学系统,试验时外部因素(接触方式、运动类型、载荷、速度、温度、时间、介质及环境气氛等)和内部因素(材料性质、表面状态、润滑剂性能等)改变时都会导致测试结果发生变化。近期的研究工作已证明人工关节磨损时产生的磨损颗粒与置换关节的无菌性松动有直接关系。因此,积极开展人工关节生物摩擦学特性方面的研究,掌握置换关节材料在生物机体环境内的摩擦磨损行为规律,在人工关节的开发中引入摩擦学设计(包括基于生物力学的关节配副载荷最小化研究、假体固定的微动摩擦学行为研究和关节材料磨损颗粒生成机理及有效识别等),对于提高人工关节的使用质量,延长其临床寿命和减轻患者痛苦具有重要的现实意义。
1.2 人工髋关节模拟试验机的分析与研究
人工关节的磨损,尤其是人工髋关节的磨损,是一个重要的临床问题。人工关节的磨损不仅能造成关节假体本身的破坏而引起机械性失效,还会产生大量磨损颗粒引导假体周围骨溶解。1965年以来,研究者相继开发关节模拟实验装置,曾采用销盘磨损实验、环盘磨损实验、四球磨损实验及块环磨损实验等,但实验设备由于结构限制无法进行全尺寸关节副摩擦实验,而且在试件偶副接触方式提供的运动形式以及载荷性质上,都与关节的实际工况相距甚远。因此,要求新的模拟试验机在实验室环境中能够更真实地模拟人体髋关节的运动情况及运动环境,为不同髋关节材料的临床应用提供较为准确可靠的试验数据。
困扰关节模拟试验机发展的一个重要因素是试验机工位太少。大多数试验机在一次试验过程中只能容纳一个关节摩擦副,在这种试验设备上完成2×106~3×106转(相当于关节假体在病人体内2~3年的运动量)的试验工作需要2~3个月的时间。针对这一问题,研究者提出了多工位试验机的概念。到目前为止,有各种多工位试验机乃至100工位的试验机在研究中使用。多工位试验机可同时进行多副人工关节偶件对比试验,因此试验周期短,对试验数据的对比分析可靠度高
1.3人工髋关节假体材料的性能要求
- 内容简介:
-
中文译文液压支架的最优化设计摘要本文介绍了从两组不同参数的采矿工程所使用的液压支架中选优的流程。这种流程建立在一定的数学模型之上。第一步,寻找四连杆机构的最理想的结构参数以便确保支架的理想的运动轨迹有最小的横向位移。第二步,计算出四连杆有最理想的参数时的最大误差,以便得出最理想的、最满意的液压支架。关键词 四连杆机构 优化设计 精确设计 模糊设计 误差1前言设计者的目的时寻找机械系统的最优设计,导致的结果是一个系统所选择的参数是最优的。一个数学函数伴随着一个合适的系统的数学模型的出现而出现。当然这数学函数建立在这种类型的系统上。有了这种数学函数模型,加上一台好的计算机的支持,一定能找出系统最优的参数。Harl描述的液压支架是斯洛文尼亚的Velenje矿场的采煤设备的一个组成部分,它用来支护采煤工作面的巷道。它由两组四连杆机构组成,如图2所示四连杆机构AEDB控制绞结点C的运动轨迹,四连杆机构FEDG通过液压泵来驱动液压支架。图2中,支架的运动,确切的说,支架上绞结点C点竖向的双纽线的运动轨迹要求横向位移最小。如果不是这种情况,液压支架将不能很好的工作,因为支架工作在运功的地层上。实验室测试了一液压支架的原型。支架表现出大的双纽线位移,这种双纽线位移的方式回见少支架的承受能力。因此,重新设计很有必要。如果允许的话,这会减少支架的承受能力。它能决定去怎样寻找最主要的四连杆机构数学模型AEDB的最有问题的参数a1,a2,a4,否则的话这将有必要在最小的机构AEDB改变这种设计方案。上面所罗列出的所有问题的解决方案将告诉我们关于最理想的液压支架的答案。真正的答案将是不同的,因为系统有各种不同的参数的误差,那就是为什么在数学模型的帮助下,参数al,a2,a4允许的最大的误差将被计算出来。2液压支架的确定性模型 首先,有必要进一步研究适当的液压支架的机械模型。它有可能建立在下面所列假设之上: (1)连接体是刚性的; (2)单个独立的连接体的运动是相对缓慢的液压支架是只有一个方向自由度的机械装置。它的运动学规律可以通过同步的两个四连杆机构FEDG和AEDB的运动来模拟。最主要的四连杆机构对液压支架的运动规律有决定性的影响。机构2只是被来通过液压泵来驱动液压支架绞结点C的运动轨迹L可以很好地来描述液压支架的运动规律。因此,设计任务就是通过使点C的轨迹尽可能地接近轨迹K来找到机构1的最理想的连接长度值。四连杆机构1的综合可以通过Rao和Dukkipati给出运动的运动学方程式的帮助来完成。图3描述了一般的情况。点C的轨迹L的方程式将在同一框架下被打印出来。点C的相对应的坐标x和y随着四连杆机构的独有的参数a1,a2, a6一起被打印出来。点B和D的坐标分别是 (1) (2) (3) (4) 参数a1,a2, a6也彼此关联 (5) (6)把(1)(4)代入(5)(6)即可获得支架的最终方程式 (7) (8)此方程式描述了计算参数a1,a2,a4的理想值的最基本的数学模型。2.1数学模型Haug和Arora提议,系统的数学模型可以用下面形式的公式表示min f(u,v), (9)约束于 i=1,2,l (10)和响应函数 j=l,2,m (11)向量u=u1 unT响应设计时的变量,v=v1 vmT是可变响应向量,(9)式中的f是目标函数。为了使设计的主导四连杆机构AEDB达到最佳,设计时的变量可被定义为u= a1 a2 a4T, (12)可变响应向量可被定义为v=x yT (13)相应复数a3,a5,a6的尺寸是确定的。目标函数被定义为理想轨迹K和实际轨迹L之间的一些“有差异的尺寸”f(u,v) =maxg0(y) f0(y)2 (14)式中x= g0(y)是曲线K的函数,x= f0(y)是曲线L的函数。我们将为系统挑选一定局限性。这种系统必须满足众所周知的最一般的情况。 (15) (16)不等式表达了四连杆机构这样的特性:复数a2,a4只可能是振荡的。这种情况: (17)给出了设计变量的上下约束条件。用基于梯度的最优化式方法不能直接的解决(9)-(11)的问题。min un+1 (18)从属于, i=1,2,1 (19) (20)并响应函数 j=l,2,m (21)式中: u=u1un un+1T v=v1vn vn+1T 因此,主导四连杆机构AEDB的一个非线性设计问题可以被描述为:min , (22) 从属于约束 (23) (24), (25) (26)并响应函数: (27) (28)有了上面的公式,使得点C的横向位移和轨迹K之间的有最微小的差别变得可能。结果是参数a1,a2,a4有最理想的值。3液压支架的随机模型 数学模型可以用来计算比如参数a1,a2,a4确保轨迹L和K之间的距离保持最小。然而端点C的计算轨迹L可能有些偏离,因为在运动中存在一些干扰因数。看这些偏离到底合时与否关键在于这个偏差是否在参数a1,a2,a4容许的公差范围内。 响应函数(27) - (28)允许我们考虑响应变量v的矢量,这个矢量依赖设计变量v的矢量。这就意味着,函数h是数学模型(22) - (28)的基础,因为它描述出了响应变量v的矢量和设计变量v的矢量以及和数学模型中v的关系。同样,函数h用来考虑参数以a1,a2,a4的误差值a1,a2,a4的最大允许值。 在随机模型中,设计变量的矢量u=u1unT可以被看作U=U1UnT的随机矢量,也就是意味着响应变量的矢量v=v1vmT也是一个随机矢量V=V1VmT (29) 假设设计变量U1Un从概率论的观点以及正常的分类函数UkN(k, k)(k=l,2,n)中独立出来。主要参数k和k (k=l,2,n)可以与如测量这类科学概念和公差联系起来,比如。所以只要选择合适的存在概率 k=1,2,n (30)式(30)就计算出结果。随机矢量V的概率分布函数被探求依赖随机矢量U概率分布函数及它实际不可计算性。因此,随意矢量V被描述借助于数学特性,而这个特性被确定是利用Tavlor的有关点u=u1unT的函数h逼近描述,或者借助被Oblak和Harl在论文提出的Monte Carlo的方法。4有数字的实列 液压支架的工作阻力为1600kN。以及四连杆机构AEDB及FEDG必须符合以下要求: 它们必须确保铰接点C的横向位移控制在最小的范围内, 一它们必须提供充分的运动稳定性 图2中的液压支架的有关参数列在表1中。 支撑四杆机构FEDG可以由矢量 b1+b2+b3+b4T=400,(1325+d),1251,1310T (mm) (31) 来确定。 四连杆AEDB可以通过下面矢量关系来确定。 a1+a2+a3+a4T= 674,1360,382,1310T (mm) (32)在方程(31)中,参数d是液压支架的移动步距,为925mm四连杆AEDA的杆系的有关参数列于表2中。表1液压支架的参数 表2四连杆AEDA的参数 4.1四连杆AEDA的优化四连杆的数学模型AEDA的相关数据在方程(22) - (28)中都有表述。(图3)铰接点C双纽线的横向最大偏距为65mm。那就是为什么式(26)为 (33) 杆AA与杆AE之间的角度范围在76.8和94.8之间,将数x1,x2,x19依次导入公式(33)中所得结果列于表3中。 这些点所对应的角,都在角度范围76.8,94.8内而且它们每个角度之差为1。 设计变量的最小和最大范围是 u = 640,1330 ,1280 ,0T (mm) (34) = 700,1390,1340,30 T (mm) (35) 非线性设计问题以方程(22)与(28)的形式表述出来。这个问题通过 Kegl et al(1991)提出的基于近似值逼近的优化方法来解决。通过用直接的区分方法来计算出设计派生数据。 设计变量的初始值为0a1,0a2,0a4,0a7T= 674,1360,1310,30T (mm) (36)忧化设计的参数经过25次反复计算后是表3 绞结点C对应的x与y的值u* = 676 .42,1360 .74,1309 .88,3.65T (mm) (37)在表3中C点x值与y位分别对应开始设计变量和优化设计变量。图4用图表示了端点C开始的双纽线轨迹L(虚线)和垂直的理想轨迹K(实线)。水基液压系统传统上水基液压系统已经应用在钢铁厂炼铁领域。这些产业中水基液压系统的明显的优点是它们的耐火性。而且水基液压系统在费用上也优于油基的液压系统。首先,无毒的、可被生物分解的综合性添加剂每加仑花费5到6美元。一加仑集中可生成20加仑的5%溶液,因此实际上水基液压流体的费用可以比油基的每加仑少30分。在工厂的水平下,考虑到相关费用、防止和清理环境的污染,水基液压系统拥有节省巨大成本的潜力。液压油的泄漏已经成为一个非常重要的问题。它必须被收集、妥善控制。不过,含有合成添加剂的水,可以倾倒入工厂的污水系统。在工厂水平下,节省成本不停留在流体的较低成本及其处理上。因为水基液压由十部分水和一部分合成添加剂,5加仑添加剂与水的混合物构成100加仑水基流体。50加仑的容器当然要比两个55加仑的桶更容易处理,因此储藏更简单、更清洁、更不凌乱,运输成本也较低。其他工厂范围下潜在的节约是为工人改善安全,因为水基液是不含毒性,并且非易燃。这些特点可以减少工厂的保险费率。泄漏的成本比清理低,因为不再需要颗粒吸收剂或吸附棉条。水基流体再次变成“热门话题”在20世纪70年代石油禁运引发了较低成本的水基液压流体替代高昂的液压油的兴趣。当设计师们获悉,一加仑聚合物可以制造出二十加仑的流体时,即使是最昂贵的水添加剂都更有吸引力。由于石油价格逐渐的回落,因此人们对水基液压也没有那么大的兴趣了。回想起来,对水基流体的兴趣集中在其节约成本的潜力上。当设计师发现他们不能在他们的系统中改变流体从液压油到水的状况并且也没有其他重大的改变时,他们就失去了兴趣。然后,他们不情愿的接受其他的“缺点”,了解到很大的变化,又切换到水基液压。适用于水基液压系统的不同的规则被认为是缺点。设计师们可能不愿意学习更多关于水基液压,因为他们被暗示,所有的工作需要依靠如何设计一个新的系统或改造旧系统的知识。因为他们结束了对这另外技术的思维,他们错过了除水基流体初始成本以外的许多其他的优点。现在,环境问题,添加了液压油处理成本的价格,水基液压便再次成为热门话题。抵抗凝固当然,水基液压系统确实在应用上有它的局限性。一个限制就是潜在的凝固。这个可能性可能是更广泛的应用水基系统,特别是在移动设备上最重要的阻碍。长壁开采法是迄今为止最大的能够充分利用水基系统的移动设备部门。地下的温度不接近水的凝点和耐火性是必不可少的条件。用于温带气候海上设备和移动设备获利于水基系统的优点,但不能保证这些设备将始终用于在上述凝固温度。不过,给水基流体加入防冻液可以使其凝固温度远低于32华氏度。用在汽车上的防冻液乙二醇是有毒的,是不能生物降解的,因此它在水基液压系统中添加防冻液将击败水基液压流体在环境上的优势。有一个替代的方法。丙二醇是没有毒性,而且是可生物降解的。它比乙二醇花费更多,并且是不太有效的一种防冻液,因此它必须使用较高浓度的溶液。减少凝固潜力的另外两门技术是要保持流体的不断循环和在实际中使用胶管。系统的密封水基液压系统的两个个容易被察觉的问题是细菌的大批出没,并且很难保持适当的浓度。大气下的密封系统在控制中可容纳细菌成长。此外,如果从系统排除空气,一个抗菌剂的流体能对防止细菌的增长有一个持久的影响。一个被密封的水箱消除许多液压系统遭受的另一个问题:水的进入。这说明关于水基系统的另一个误解:没有从大气中密封的水基系统,必须密切监察,以确保该添加剂浓度保持在允许的范围之内,这是因为水比添加剂更容易从水箱蒸发。因此,水分蒸发导致添加剂浓度增加。当新液体添加到系统时,现有的流体样本必须采取措施,以确定一定浓度的添加剂在溶液中。这些结果显示,添加剂在流体中的比例必须补充,使流体的浓度是合适的。与大气隔绝的密封的流体系统,实际上消除了蒸发问题。泄漏的液体是包含水和添加剂的。所以,系统流体的量在发生变化,但浓度没有变化。系统流体通过增加水和添加剂的一种预先混合重新补充到水箱。英文原文Optimal design of hydraulic supportAbstract This paper describes a procedure for optimal determination of parameters of hydraulic support employed in the mining industry. The procedure is based on mathematical programming methods. In the first step,the optimal values of some parameters of the leading four-bar mechanism are found in order to ensure the desired motion of the support with minimal transversal displacements. In the second step,maximal tolerances of the optimal values of the leading four-bar mechanism are calculated,so the response of hydraulic support will be satisfying.Keywords four-bar mechanism,optimal design,mathematical programming,approximation method,tolerance1.IntroductionThe designer aims to find the best design for the mechanical system considered. Part of this effort is the optimal choice of some selected parameters of a system. Methods of mathematical programming can be used,if a suitable mathematical model of the system is made. Of course,it depends on the type of the system. With this formulation,good computer support is assured to look for optimal parameters of the system.The hydraulic support (Fig.1) described by Harl (1998) is a part of the mining industry equipment in mine Volenje-Slovenia,used for protection of working environment in the gallery. It consists of two four-bar mechanisms FEDC and AEDB as shown in Fig.2. The mechanism AEDB defines the path of coupler point C and the mechanism FEDG is used to drive the support by a hydraulic actuator.It is required that the motion of the support,more precisely,the motion of point C in Fig.2,is vertical with minimal transversal displacements. If this is not the case,the hydraulic support will not work properly because it is stranded on removal of the earth machine.A prototype of the hydraulic support was tested in a laboratory (Grm 1992). The support exhibited large transversal displacements,which would reduce its employability. Therefore,a redesign was necessary. The project should be improved with minimal cost if possible. It was decided to find the best values for the most problematic parameters a1,a2,a4 of the leading four-bar mechanism AEDB with methods of mathematical programming. Otherwise it would be necessary to change the project,at least mechanism AEDB.The solution of above problem will give us response of hydraulic support for the ideal system. Real response will be different because of tolerances of various parameters of the system.,which is why the maximal allowed tolerances of parameters a1,a2,a4 will be calculated,with help of methods of mathematical programming.2.The deterministic model of the hydraulic supportAt first it is necessary to develop an appropriate mechanical model of the hydraulic support. It could be based on the following assumptions:- the links are rigid bodies.- the motion of individual links is relatively slow.The hydraulic support is a mechanism with one degree of freedom. Its kinematics can be modeled with synchronous motion of two four-bar mechanisms FEDG and AEDB (Oblak et al.1998). The leading four-bar mechanism AEDB has a decisive influence on the motion of the hydraulic support. Mechanism 2 is used to drive the support by a hydraulic actuator. The motion of the support is well described by the trajectory L of the coupler point C. Therefore,the task is to find the optimal values of link lengths of mechanism 1 by requiring the trajectory of the point C is as near as possible to the desired trajectory K.The synthesis of the four-bar mechanism 1 has been performed with help of kinematics equations of motion given by Rao and Dukkipati (1989). The general situation is depicted in Fig.3.Equations trajectory L of the point C will be written in the coordinate frame considered. Coordinates x and y of the point C will be written with the typical parameters of a four-bar mechanism a1,a2, a6 . The coordinates of points B and D are (1) (2) (3) (4) The parameters a1,a2, a6 are related to each other by (5) (6)By substituting (1)(4) into (5)(6) the response equations of the support are obtained as (7) (8)This equation represents the base of the mathematical model for calculating the optimal values of parameters a1,a2,a4.2.1 Mathematical modelThe mathematical model of the system will be formulated in the form proposed by Haug and Arora (1979) :min f(u,v), (9)subject to constraints i=1,2,l (10)and response equations j=l,2,m (11)The vector u=u1unT is called the vector of design variables,v=v1vmT is the vector of response variables and f in (9) is the objective function.To perform the optimal design of the leading four-bar mechanism AEDB,the vector of design variables is defined asu= a1 a2 a4T, (12)and the vector of response variables asv=x yT (13)The dimensions a3,a5,a6 of the corresponding links are kept fixed.The objective function is defined as some “measure of difference” between the trajectory L and the desired trajectory K asf(u,v) =maxg0(y) f0(y)2 (14)where x= g0(y) is the equation of the curve K and x= f0(y) is the equation of the curve L.Suitable limitations for our system will be chosen. The system must satisfy the well-known Grasshoff conditions (15) (16)Inequalities (15) and (16) express the property of a four-bar mechanism,where the links a2,a4 may only oscillate. The condition (17)prescribes the lower and upper bounds of the design variables. The problems (9)-(11) is not be directly solvable with the usual gradient-based optimizations methods. This could be circumvented by introducing an artificial design variable un+1 as proposed by Hsieh and Arora (1984). The new formulation exhibiting a more convenient form may be written asmin un+1 (18)subject to, i=1,2,1 (19), (20)and response equationsj=l,2,m (21)where u=u1un un+1T and v=v1vmT .A nonlinear programming problem of the leading four-bar mechanism AEDB can therefore be defined asmin, (22) subject to constraints (23) (24), (25) (26)and response equations (27) (28)The formulation enables the minimization of the different between the transversal displacement of the point C and the prescribed trajectory K. The result is the optimal values of the parameters a1,a2,a4.3.The stochastic model of the hydraulic supportThe mathematical model (22) - (28) may be used to calculate such values of the parameters a1,a2,a4,that the “difference between trajectories L and K” is minimal.However,the real trajectory L of the point C could deviate from the calculated values because of different influences. The suitable mathematical model deviation could be treated dependently on tolerances of parameters a1,a2,a4.The response equations (27) (28) allow us to calculate the vector of response variables v in dependence on the vector of design variables u. This implies. The function h is the base of the mathematical model (22) (28),because it represents the relationship between the vector of design variables u and response v of our mechanical system. The same function h can be used to calculate the maximal allowed values of the tolerances of parameters a1,a2,a4.In the stochastic model the vector u=u1unT of design variables is treated as a random vector U=U1UnT,meaning that the vector v=v1vmT of response variables is also a random vector V=V1VmT, (29)It is supposed that the design variables U1Un are independent from probability point of view and that they exhibit normal distribution,UkN(k, k) (k=l,2,n). The main parameters k and k (k=l,2,n) could be bound with technological notions such as nominal measures,k= k and tolerances,e.g.,so events, k=l,2,n (30)will occur with the chosen probability.The probability distribution function of the random vector V,that is searched for depends on the probability distribution function of the random vector U and it is practically impossible to calculate. Therefore,the random vector V will be describedwith help of “numbers characteristics”,that can be estimates by Taylor approximation of the function h in the point u=u1unT or with help of the Monte Carlo method in the papers by Oblak (1982) and Harl (1998).4. Numerical example The carrying capability of the hydraulic support is 1600 kN. Both four-bar mechanisms AEDB and FEDG must fulfill the following demand:- they must allow minimal transversal displacement of the point C- they must provide sufficient side stabilityThe parameters of the hydraulic support (Fig.2) are given in Table 1.The drive mechanism FEDG is specified by the vector b1+b2+b3+b4T=400,(1325+d),1251,1310T (mm) (31)And the mechanism AEDB by a1+a2+a3+a4T= 674,1360,382,1310T (mm) (32)In (31),the parameter d is a walk of the support with maximal value of 925mm. Parameters for the shaft of the mechanism AEDB are given in Table 2.4.1 Optimal links of mechanism AEDB With this data the mathematical model of the four-bar mechanisms AEDB could be written in the form of (22) (28). A straight line is defined by x=65(mm)(Fig.3) for the desired trajectory of the point C. That is why condition (26)is (33)The angle between links AB may vary between 76.8 and 94.8. The condition (33) will be discredited by taking into account only the points x1,x2,x19 in Table 3. These points correspond to the angles of the interval 76.8,94.8 at regular intervals of 1.The lower and upper bounds of design variables are u = 640,1330 ,1280 ,0T (mm) (34) = 700,1390,1340,30 T (mm) (35)The nonlinear programming problem is formulated in the form of (22) (28). The problem is solved by the optimizer described by Kegl et al. (1991) based on approximation method. The design derivatives are calculated numerically by using the direct differentiation method.The starting values of design variables are0a1,0a2,0a4,0a7T= 674,1360,1310,30T (mm) (36)The optimal design parameters after 25 iterations areu* = 676 .42,1360 .74,1309 .88,3.65T (mm) (37)In Table 3 the coordinates x and y of the coupler point C are listed for the staring and optimal designs,respectively.Figure 4 illustrates the trajectories L of the point C for the starting (hatched) and optimal (full) design as well as the straight link K.Water-based hydraulic systemsWater-based hydraulic systems traditionally have been used in hot-metal areas of steel mills. The obvious advantage of water system in these industries is their fire resistance. Water-based hydraulic systems also have obvious cost advantages over oil-based fluid. First,non-toxic,biodegradable synthetic additives for water cost 5to 6 per gallon. One gallon of concentrate can make 20 gallons of a 5% solution,so the cost of water-based hydraulic fluid actually can be less than 30 cents per gallon.Considering the costs associated with preventing and cleaning up environmental contamination,water-based hydraulic systems hold the potential for tremendous cost saving at the plant level. Oil that has leaked already becomes a very important problem. It must be collected ,properly contained. Water containing synthetic additives,however,can by dumped into plant effluent systems.Costs saving at the plant level dont stop at the lower cost of the fluid and its disposal. Because water-based hydraulic fluid consists of 10 parts water and one part synthetic additives,5 gallons of additive mixes with water to make 100 gallons of water-based fluid. A 50 gallon container is certainly easier to handle than two 55 gallon drums,so warehousing is simple,cleaner,and less cluttered. Transportation costs also are lower.Other potential plant-wide saving include improved safety for workers because the water-based fluid is non-toxic as well as non-flammable. These attributes can reduce plant insurance rate. Spills cost less to clean up because granular absorbents or absorbent socks are unnecessary. Water is “hot” again.The oil embargo in the 1970s sparked interest in water-based fluids as a less-costly alternative to oils. Even the most expensive water additives became attractive when designers learned that one gallon of concentrate would make 20 gallons of fluid.As oil prices gradually dropped,so did interest in water-based hydraulics. In retrospect,interest in water-based fluids centered around their cost saving potential.Most designers lost interest when they discovered that they could not just change the fluid in their systems from oil to water without making other substantial changes. They then become reluctant to accept other “disadvantages”,read substantial changes of switching over to water-based hydraulics.What were viewed as disadvantages were really different rules that apply to water-based hydraulic systems? Designers probably resisted learning more about water-based hydraulic because they were intimated by all the work required to lean about how to design a new system or retrofit an older system. By closing their minds to this different technology,they missed the many other advantage of water-based fluid beyond initial cost. Now that environment concerns have added disposal costs to the price of hydraulic fluids,water-based hydraulics has again become a hot topic.Fighting freezeWater-based hydraulic systems do,of course,have limits to their applications. One limitation is the potential of freezing. This possibility is probably the most significant blockade to more widespread application of water-based systems,especially in the mobile equipment industry. Longwall mining is by far the largest sector of mobile equipment that has been able to take advantage of water-based systems. Temperatures undergrou
- 温馨提示:
1: 本站所有资源如无特殊说明,都需要本地电脑安装OFFICE2007和PDF阅读器。图纸软件为CAD,CAXA,PROE,UG,SolidWorks等.压缩文件请下载最新的WinRAR软件解压。
2: 本站的文档不包含任何第三方提供的附件图纸等,如果需要附件,请联系上传者。文件的所有权益归上传用户所有。
3.本站RAR压缩包中若带图纸,网页内容里面会有图纸预览,若没有图纸预览就没有图纸。
4. 未经权益所有人同意不得将文件中的内容挪作商业或盈利用途。
5. 人人文库网仅提供信息存储空间,仅对用户上传内容的表现方式做保护处理,对用户上传分享的文档内容本身不做任何修改或编辑,并不能对任何下载内容负责。
6. 下载文件中如有侵权或不适当内容,请与我们联系,我们立即纠正。
7. 本站不保证下载资源的准确性、安全性和完整性, 同时也不承担用户因使用这些下载资源对自己和他人造成任何形式的伤害或损失。

人人文库网所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
 川公网安备: 51019002004831号
川公网安备: 51019002004831号