For two months, My graduation design is the overall design of the formula racing. we used the contrast analysis method mainly in the design, through optimizing the parameters optimization design and optimization of UG MATLAB, etc.

Initial stage, we according to 2012 auto contest rules determine college equation overall layout of the car, and the demonstration and analysis, the main parameter is determined primarily racing. Through calculation and comparison, sure engine type, primaries drivetrain maximum transmission ratio, minimum transmission.

The intermediate stage, we design UG7.0 3d software used in various parts of assembly for modeling and whole assembly, and suspension, steering movement interference analysis. Use of engine power characteristic curve characteristic, MATLAB software mapped drive car driving forces - resistance balance figure, acceleration curve, and etc, and detailed calculation racing fuel economy.

The final stages UG7.5 are derived by car, general layout, and two-dimensional engineering graphics overall parameter table, and made the third generation and the second generation racing cars are compared and analyzed. For considering the actual production of may change suspension, frame and steering parts, obligate scheme.

Through the graduation design, I understand and master the overall design of car of the steps and method, the professional knowledge of professional knowledge, enhance the data collection and integration of information, these ability after my graduation will be engaged in car design lay a good foundation for the job.

KEY WORDS: FSAE, general parameters, parameter identification, general arrangement,the car power, fuel economy

第一章 FSAE赛车概述1

§1.1 FSAE赛车起源1

§1.2 FSAE赛车现状2

§1.2.1 国际赛车概述2

§1.2.2 国内及我校赛车概述2

§1.3 FSAE 总体设计概述3

§1.3.1 汽车设计的方法及过程3

§1.3.2 FSAE赛车的技术要求4

§1.3.3 我校第三代赛车设计目标4

§1.3.4 FSAE赛事意义5

第二章 FSAE赛车总体设计7

§2.1 总体设计目标7

§2.2 赛车目标参数的初步确定8

§2.2.1 发动机选择9

§2.2.2 轮胎的选择10

§2.2.3 传动系最小传动比的确定11

§2.2.4 传动系最大传动比的确定11

§2.3 赛车发动机选型12

§2.4 赛车主要设计参数的确定13

§2.4.1 尺寸参数13

§2.4.2 质量参数14

§2.4.3 性能参数15

§2.5 赛车各系统设计17

§2.5.1 悬架系统设计18

§2.5.2 转向系统设计19

§2.5.3 制动系统设计19

§2.5.4 电器系统设计21

§2.5.5 车身设计23

§2.5.6 车架设计23

第三章赛车动力性与燃油经济性25

§3.1 赛车的动力性25

§3.1.1 动力性的评价指标25

§3.1.2驱动力—行驶阻力图25

§3.1.3 汽车的加速能力28

§3.1.4 动力特性图29

§3.1.5 功率平衡31

§3.2 燃油经济性32

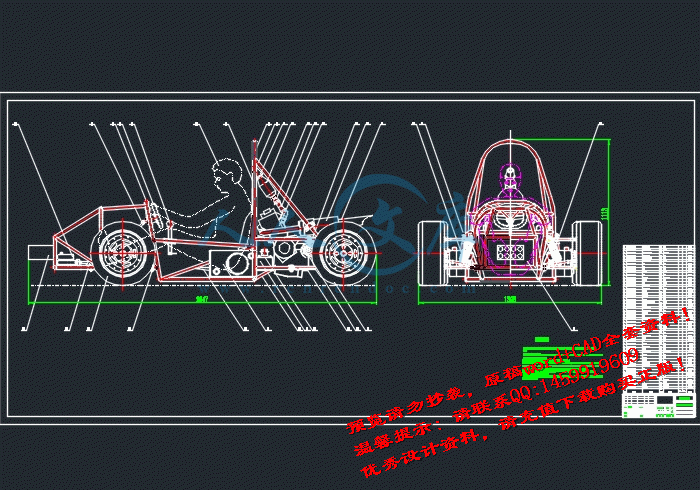
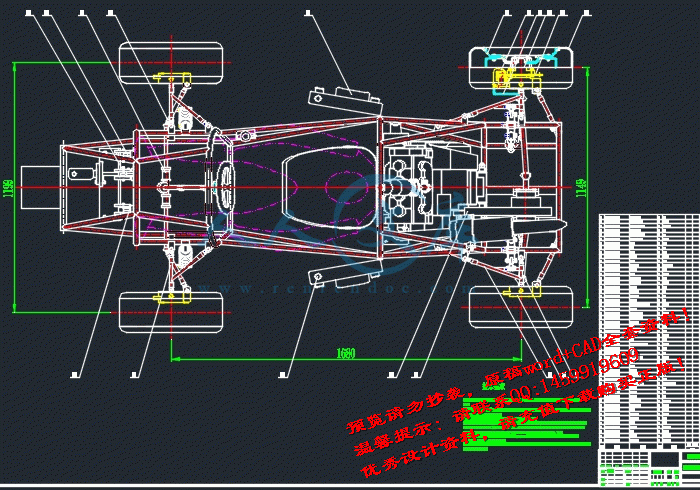
第四章赛车总体布置33

§4.1 整车布置的基准线（面）-零线的确定34

§4.2 各部件的布置35

§4.3 总体设计参数表38

第五章结论40

参考文献41

致谢42

第一章 FSAE赛车概述

Formula SAE 赛事1980年在美国举办第一次比赛以来，现在已经成为汽车工程学会的学生成员举办的一项国际赛事，其目的是设计、制造一辆小型的高性能方程式赛车，并使用这辆自行设计和制造的赛车参加比赛。

出于此项比赛的宗旨是让学生针对业余高速穿障的车手开发制造一个原型车，该原行车应该具备有可小批量生产的能力，并且原型车的造价要低于25,000 美元。这项竞赛包含有3 个最主要的基本元素，分别是：工程设计、成本控制以及静态评估、单独的动态性能测试、高性能的耐久性测试。

Formula SAE 赛事的主要参与者通常都是来自高校的学生组成的车队。现在在美国、欧洲和澳大利亚每年都会举办Formula SAE 比赛。Formula SAE 向年轻的工程师们提供了一个参与有意义的综合项目的机会。由参与的学生负责管理整个项目，包括时间节点的安排，做预算以及成本控制、设计、采购设备、材料、部件以及制造和测试。

§1.1 FSAE赛车起源

第一届SAE Mini Baja比赛于1976 年举办，并且迅速成为一个地区性的年度比赛。比赛由三个评判标准组成，即静态比赛：设计、成本、陈述；接着是各自的性能竞赛2项目。 Mini Baja比赛重点强调了底盘的设计，因为每个队伍都使用一个8匹马力的引擎。在过去的20 多年里，SAE Mini Baja 的成功超乎了每个人的预期。

参考文献

[1] 张文春，汽车理论，机械工业出版社，2007.11，22-44

[2] 刘惟信，汽车设计，清华大学出版社，2001.7

[3] 陈家瑞，汽车构造（第二版下册），机械工业出版社，2005.1，98-116

[4] 王望予，汽车设计（第四版），机械工业出版社，2009.1，1-50

[5] 张洪欣，汽车设计，机械工业出版社，1983.3, 7-47

[6] 自动车技术会小林明，汽车工程手册（第二分册），机械工业出版社，

1984.4， 386-419

[7] 编辑委员会，汽车工程手册摩托车篇，人民交通出版社，2001.3 ，170-188

[8] 机械设计手册编委会，机械设计手册新编，机械工业出版社，2004.8,16-44--16-66

[9] 中国汽车技术研究中心，汽车设计标准资料手册（金属篇），河北抚宁印刷，1994.10, 357-358

[10] 长春汽车研究所编.悬架设计.汽车技术，1973，第五期 ,34-36

[11] 东北大学组编.机械零件·设计手册.，冶金工业出版社，1994，268-281

[12] 吴宗泽.机械设计实用手册.，化学工业出版社，2001,

[13]王昆，何小柏，汪信远.机械设计基础课程设计.，高等教育出版社，2004

[14] 汽车工程手册编委会编.汽车工程手册.设计篇.，人民交通出版社，2001

[15] 汽车工程手册编委会编.汽车工程手册.基础篇.，人民交通出版社，2001

[16] 神龙汽车有限公司编著.中国轿车丛书：富康.，北京理工大学出版社，1998

[17] 吴子牛，王兵，周睿，空气动力学（上册），清华大学出版社，2007.1

[18] 常思勤，汽车动力装置，机械工业出版社，2006.2

内容简介：: Dynamic Characteristics on the Dual-Power State of Flow in Hydro-Mechanical Transmission Jibin Hu and Shihua Yuan Xiaolin Guo School of Mechanical and Vehicular Engineering Department of Automotive Engineering Beijing Institute of Technology Tsinghua University Beijing 100081, China Beijing 100084, China hujibin & yuanshihua guoxiaolin Abstract In order to study the dynamic characteristics of a hydro-mechanical transmission (HMT) system, a bond graph model of the dual-power state of flow of the two ranges HMT system is established based on the bond graph theory. Taking the elements at the state variables, the state equations of the system are deduced. Based on this model, dynamic response of the HMT system is simulated. The response characteristics of output speed and systemic pressure of the HMT are given when the load, input speed and angle of slope plate of the pump change by their respective rules, and the influence of fluid volume is analyzed. The results of analysis illustrates that the HMT system needs less than 0.5s to attain the steady state in its dynamic response and will take longer when the fluid volume is increased. Index Terms Hydro-mechanical transmission, Bond graph, Dynamic characteristic I. INTRODUCTION Hydro-mechanical transmission (HMT) system is composed of hydrostatic transmission and mechanical transmission. The power flow in the hydrostatic transmission branch and the opposite in the mechanical branch are transmitted to the system output shaft through the differential mechanism in the form of power conflux. Continuously variable ratio will be obtained as the displacement of variable displacement hydrostatic unit is altered. As a type of continuously variable transmission (CVT), Hydro-mechanical transmission (HMT) system has been in use in the direct propulsion and steering system of military tracked vehicles. But, recent researches on Hydro-mechanical transmission are mainly focused on structures and static characteristics. With the application of the theory of power bond graph, we built a bond graph model of a two ranges hydro-mechanical transmission system, and simulated its dynamic characteristics. II. MODEL OF THE HMT SYSTEM A. Schematic of the HMT system The basic components of a two ranges Hydro-mechanical continuously variable transmission system are shown in Fig.1. The system consists of several components: three clutches, four planetary gear trains (PGT), a variable displacement hydrostatic unit and a fixed displacement hydrostatic unit. Planetary gear train P2and P3will work alone on conditions that clutch CLengaged and CH, CRdisengaged. It characterizes the dual-power flow mode of the two ranges HMT system. Meanwhile, the power input at gear Z1is split into two paths by gear Z21and Z22. One power input is transmitted to the hydrostatic transmission units through gear Z3. Another is transmitted to the mechanical transmission units through gear Z4. These two power flow are finally united at planetary gear train P2and transmitted to the downstream components of driveline through gears Z5, Z6and Z7. Fig. 1 Schematic of the HMT system B. System modeling According to the analyses of power flows of the hydro-mechanical transmission (HMT) system showed in Fig.1, a bond graph model of the dual-power state of flow of the system is established (shows in Fig.2), based on the bond graph theory. In Fig.2, all bonds have been numbered. Variables in different bonds can be identified by corresponding serial numbers as suffixes. For instance, effect variable and flow variable in bond 25 can be respectively denoted as e25and f25. Symbols in bond graph can be defined as follows: n0stands for power source and can be taken for a flow source, because it is speed input source of the system. Tbis load of the system and can be taken for an effect source, because it is torque input source of the system. pdlis a compensator, it is taken for a effect source here in order to keep invariable pressure in low pressure oil pipe of the hydrostatic loop. io is InputOutput1-4244-0828-8/07/$20.00 2007 IEEE. 890Proceedings of the 2007 IEEEInternational Conference on Mechatronics and AutomationAugust 5 - 8, 2007, Harbin, Chinantstransmission ratio from gear Z1to Z21; ijzis the mechanical path ratio. ipis the transmission ratio from gear Z22to Z3. ihzis the conflux ratio of mechanical path. ihyis the conflux ratio of hydrostatic path. ibis the transmission ratio from gear Z5to Z7. MTF1is the variable displacement hydrostatic unit and can be describe as a variable gyrator. The modulus of the gyrator is decided by parameter qpof the signal generator. qmand qmlstand for conversion gain coefficient of the fixed displacement hydrostatic unit, furthermore, qm qml=1. 1-junction is a co-flow node in which flow variables is equal. 0-junction is a co-effect node in which effect variables is equal. 10 2019181716151413121129 28 27 26 25 24 2322219 8 7 6 5 4 3 2 1 5958575650 55 553 52 51 4847 46 4544434249 4140393837363534333231301 I Io R g541o MTF MTF1 010 TFqmSfno SeTbRRpCCpIIglCCmRRm1 R g541fmRg541bIIbI Im10 C Co 0 C CbRRgl1TF ihy 10 1TFqm1RRdlIIdlTF io R g541fp I Ip 1 Se pdl TFip 1 TF ib 0 0 1 TFihzRg541jz1IIjz1C Cjz1 011TFijzRg541jz3CCjz2IIjz3IIjz2Rg541jz2qp Fig.2 Bond graph model of the HMT system g1000is coefficient of viscous friction on input shaft (Ns/m). g100fpis coefficient of viscous friction counteracting the rotation of the variable displacement hydrostatic unit. g100fmis coefficient of viscous friction counteracting the rotation of the fixed displacement hydrostatic unit. g100bis coefficient of viscous friction on output shaft. Rglis leakage fluid resistance of oil in high pressure hydrostatic loop (Ns/m5). Rdlis leakage fluid resistance of oil in low pressure hydrostatic loop. Rpis leakage fluid resistance of oil in the variable displacement hydrostatic unit. Rmis leakage fluid resistance of oil in the fixed displacement hydrostatic unit. g100jz1is coefficient of viscous friction in drive shafting of the mechanical path transmission. g100jz2is coefficient of viscous friction in driven shafting of the mechanical path transmission. g100jz3is coefficient of viscous friction in conflux shafting. Cois coefficient of pliability of the input shaft (m/N). Cbis coefficient of pliability of the output shaft. Cpis the fluid capacitance of inner oil in the variable displacement hydrostatic unit (m5/N). Cmis the fluid capacitance of inner oil in the fixed displacement hydrostatic unit. Cjz1is coefficient of pliability of the drive shafting of the mechanical path transmission. Cjz2is coefficient of pliability of the driven shafting of the mechanical path transmission. Iois the moment of inertia of the input shaft. Ipis the moment of inertia of the variable displacement hydrostatic unit. Imis the moment of inertia of the fixed displacement hydrostatic unit. Ibis the moment of inertia of the output shaft. Iglis the fluid inductance in high pressure oil loop (Ns/m5). Idlis the fluid inductance in low pressure oil loop. Ijz1is the moment of inertia of the drive shafting of the mechanical path transmission. Ijz2is the moment of inertia of the driven shafting of the mechanical path transmission. Ijz3is the moment of inertia of the conflux shafting. C. State equations of the HMT system Analyzing the dynamic characteristic of system using bond graph methods need to choose state variables of system reasonably and establish state equation of the system according to the known bond graph model of system. In a general way, the generalized momentum p of inertial unit and the generalized displacement of capacitive unit are introduced as state variables of system 510. If causalities of the bond graph are annotated according to principle of priority of the integral causality, some energy storage elements in bond graph maybe have differential causality on occasion. Under the circumstances, the amount of state variables of the system is equal to the counterpart of energy storage elements which have the integral causality. Energy variables of the energy storage elements which have the differential causality depend upon state variables of the system. These variables are dependent variables. Algebraic loop problem will occur while establishing state equation of 891ntsthese kinds of bond graph. The bond graph model of the HMT system established as above belongs to these kinds. In Fig.2, energy variables in inertial elements Io, Ijz2and Imhave differential causalities. The resolution is to express the generalized momentum and the generalized displacement of energy storage elements which have the differential causality with involved state variables and to work out the first derivative of these equations toward time. The expressions of the inertial elements Io, Ijz2and Imare derived as follows: 274pIIiippopog6g6 g32(1) 111215pIiIpjzjzjzg6g6 g32(2) 43149pIqIpdlmmg6g6 g32(3) Therefore, the amount of state variables of the HMT system is just 12: )(2tq, )(9tq, )(11tp,)(18tq,)(20tp, )(27tp, )(31tq,)(34tp, )(37tq, )(43tp, )(55tq, )(58tp. The input state vector: U g62g64TbdloTpng32 . According to the structural characteristics of the system shown by bond graph, the differentials of state variables can be describe as functions of state variables related to input variables. 12 state equations can be formulated as follows: 272pIiinqppoog16g32g6(4) 2711191pIipIqppjzg14g16g32g6(5) 1821112112129111111qCiCpiICiqCCpjzjzjzjzjzjzjzjzg16g14g16g32g80g80g6(6) 2031111811pIpIiqjzjzjzg16g32g6(7) 5520331822011qCiipIqCpbbhzjzjzjzg16g16g32g80g6 (8) 272229122227pICliqCCiqCCiippopofpjzpopog80g80 g14g16g16g32g6dlppppCqtqCCqt2312)()( g72g72g14g16(9) 3431273111)(pIqCRpIqtqglppppg16g16g32g72g6 (10) 3734313411qCpIRqCpmglglpg16g16g32g6(11) 43373437111pIqCRpIqdlmmglg16g16g32g6(12) 43232373431pIqCRqqCCpdlmdlmfmmg14g16g32g80g6dlbbhympCqCiiqC355311g16g16(13) 584320355111pIpIqiipIiiqbdlmbhyjzbhzg16g14g32g6(14) bbbbTpIqCp g14g16g325855581 g80g6(15) Where, 121211jzjzjzIiIC g14g32, popoIIiiC2221g14g32, 231mdlmqIIC g14g32. III. SIMULATION RESULTS In these equations above, with the structural and calculative parameters of the known HMT system, dynamic simulation can be done in computer. In the process of simulation, initial values are given primarily. After the system stabilized, input signal is stimulated. Meanwhile, the results of dynamic response of the system are recorded. The response curves of the output speed of system and the oil pressure in main pipe of the bump-motor system under varied input signals are shown from Fig.3 to Fig.8. Fig.3 shows the pulsed response curves of the output speed and the oil pressure of the system as the load change instantaneously. The rising time of the oil pressure response is 22ms. The control time is 445ms. The overshoot is equal to 86%. Times (s) Fig. 3 Pulsed response of the system as load changing Pressure Output speed Speed response (rpm)Pressure response (MPa) 892nts Fig.4 shows the pulsed response curves of the output speed and the oil pressure of the system as the speed changes instantaneously. The rising time of the speed response is 17ms. The control time is 479ms. The overshoot is equal to 65%. Times (s) Fig. 4 Pulsed response of the system as speed changing Fig.5 shows a group of slope response curves as the angle of swing plate of the variable displacement bump is a ramp excitation. In this figure, the ascending gradients of the angle of swing plate whose range is from 0 to its maximum (correspondingly, relative rate of changing displacement is from 0 to 1, i.e. 10g32g72 ) are assigned some values respectively, such as 50, 20, 8, 4 (corresponding rising time for ramp excitation are 0.04, 0.10, 0.25, 0.50s). The rising times of response of the output speed are 43, 108, 255, 505 ms. Overshoot are respectively 47%, 12%, 4%, 2%. Times (s) Fig. 5 Slope response of the system as angle of swing plate changing Fig.6 shows the pulsed response curves of the output speed and the main oil pressure of the system as the angle of swing plate changes instantaneously. The rising time of the speed response is 22ms. The control time is 420ms. The overshoot is equal to 73%. The bond graph model of the two range HMT system established by the author is a linear system. The results of simulation demonstrate that the speed of response of the system is quite fast and the stability is satisfactory, but the overshoot of step response is too large. On condition that the input signal is ramp type and the gradients is greater than 8 (the time interval in which the angle of swing plate changed from 0 to the maximum is not less than 0.25s), the transition process of the system whose overshoot will not exceed 5% will approach steady state. Times (s) Fig. 6 Pulsed response of the system as angle of swing plate changing The results of simulation indicated by Fig.3 Fig.6 is acquired on condition that the fluid capacitances Cmand Cpin the model denoted in Fig.2 are set to 0.0085. As other conditions are invariable, response curves indicated by Fig.7 and Fig.8 can be obtained for Cmand Cpare set to 0.0850. Fig.7 shows the slope response curves of the rotation speed and the pressure as the angle of swing plate changes on the principle of ramp excitation. The rising times of response of the output speed are 87, 121, 204, 519 ms. Overshoot are respectively 52%, 38%, 11%, 5%. Times (s) Fig. 7 Slope response of the system when Cmand Cpare set to 0.0850 Pressure Output speed Speed response (rpm)Pressure response (MPa) Pressure Output speed Speed response (rpm)Pressure response (MPa) Pressure Output speed Speed response (rpm)Pressure response (MPa) PressureOutput speed Speed response (rpm)Pressure response (MPa) 893nts Fig.8 shows the pulsed response curves of the rotation speed and the pressure. The rising time of response of the output speed is 68ms. Overshoot is 57%. Compared with the results of simulation indicated in Fig.5 and Fig.6, the speed of response of the system is slowing down and the time interval needed to reach the steady state is delayed. At the same time, the number of oscillations of the response and fluctuating quantity of the pressure is decreasing. The overshoot of the pulsed response increased a little, but the overshoot of the slope response increased a bit as well. Times (s) Fig. 8 Pulsed response of the system when Cmand Cpare set to 0.0850 IV. CONCLUSIONS A bond graph model of the dual-power state of flow of the two ranges HMT system is established based on the bond graph theory. The model can be applied to simulate and study the dynamic characteristics of a hydro-mechanical transmission (HMT) system. On conditions that the displacement of the hydrostatic bump is constant, the system focused in this article can be simplified to a linear stationary system. On conditions that the displacement of the hydrostatic bump changes along with time, the system is a linear time varying system; the transition of the system approaches to stable state while the ramp input signal draws 8s. The value of the fluid capacitance in the hydrostatic system affects the dynamic response performance of the system. A further study on the influence of the fluid capacitance and the fluid resistance will be done. REFERENCES 1 X. Liu, Analysis of Vehicular Transmission System, Beijing: National

温馨提示:
1: 本站所有资源如无特殊说明，都需要本地电脑安装OFFICE2007和PDF阅读器。图纸软件为CAD,CAXA,PROE,UG,SolidWorks等.压缩文件请下载最新的WinRAR软件解压。
2: 本站的文档不包含任何第三方提供的附件图纸等，如果需要附件，请联系上传者。文件的所有权益归上传用户所有。
3.本站RAR压缩包中若带图纸，网页内容里面会有图纸预览，若没有图纸预览就没有图纸。
4. 未经权益所有人同意不得将文件中的内容挪作商业或盈利用途。
5. 人人文库网仅提供信息存储空间，仅对用户上传内容的表现方式做保护处理，对用户上传分享的文档内容本身不做任何修改或编辑，并不能对任何下载内容负责。
6. 下载文件中如有侵权或不适当内容，请与我们联系，我们立即纠正。
7. 本站不保证下载资源的准确性、安全性和完整性, 同时也不承担用户因使用这些下载资源对自己和他人造成任何形式的伤害或损失。

人人文库网所有资源均是用户自行上传分享，仅供网友学习交流，未经上传用户书面授权，请勿作他用。