典型环节的频率特性

1、第5章辅导3给系统输入一个正弦信号为Xr(t) = X rm sin CO t式中 Xrm正弦输入信号的振幅； O正弦输入信号的频率。稳态输出当系统的运动达到稳态后，比较输出量的稳态分量和输入波形时就可以发现, 的频率与输入频率相同，但输出量的振幅及相位都与输入量不同。可以把系统的稳态输出量写成M t )=卫(3 *瓠"丽+邯(0力式中的A( O )和 (O )分别为复变函数 G(j O )的模和幅角。A( o ) G(j o )的模，它等于稳态输出量与输入量的振幅比，叫做幅频特性;0 (o ) G(j O )的幅角，它等于稳态输出量与输入量的相位差，叫做相频特性。例：电路的输出电压

2、和输入电压的复数比为式中>/1 + (3甲(3)= tQ(一7如人？二frC；c皿图 J?c电路频率特性的求取方法频率特性一般可以通过如下三种方法得到：1. 根据已知系统的微分方程，把输入以正弦函数代入，求其稳态解，取输出稳态分量和 输入正弦的复数之比即得；2. 根据传递函数来求取；3. 通过实验测得。线性系统，Xr(t)、Xc(t)分别为系统的输入和输出，G(s)为系统的传递函数。输入用正弦函数表示xr(t) = Asin 3 t设系统传递函数为重要结论：对正弦输入而言X百冋|G (-正弦输出对正弦输入幅值比免牆一正弦输出对正弦输入的相移G(s)中系统的频率特性可直接由G(j 3 )=

3、Xc(j 3 )/Xr(j 3 )求得。只要把线性系统传递函数的算子s换成j 3,就可以得到系统的频率特性G(j 3 )。即G(j ) G(s)频率特性的表示方法1. 幅相频率特性设系统(或环节)的传递函数为G(s)bmsmbm1sm1nn 1ansan 1 sboao令S=j 3,则其频率特性为G(j )bm(j)mnbm1(j )m1 an(j )" ani(j )n1boaoP( ) jQ()其中，P()为G(j)的实部，称为实频特性;Q()为G(j )的虚部，称为虚频特性。G(j ) JP2( ) Q2()ej式中，A()为频率特性的模，即幅频特性,A( ) JP2( ) Q

4、2()；()为频率特性的幅角或相位移，即相频特性,()arctanOU。P()2. 对数频率特性Bode)对数频率特性是将频率特性表示在对数坐标中。对数频率特性曲线又称为伯德( 图，它包括对数幅频和对数相频两条曲线。对式两边取对数，得lgG(j ) lgA( ) j ( )lge Ig A( )jO.434 ()这就是对数频率特性的表达式。通常不考虑0.434这个系数，而只用相位移本身。在实际应用中，频率特性幅值的对数值常用分贝(dB，decibel)表示，其关系式为L( ) 20lg A( )dB横坐标为频率，但按lg刻度。因此，频率每变化十倍，横坐标轴上就变化一个单位 长度，称为“十倍频程

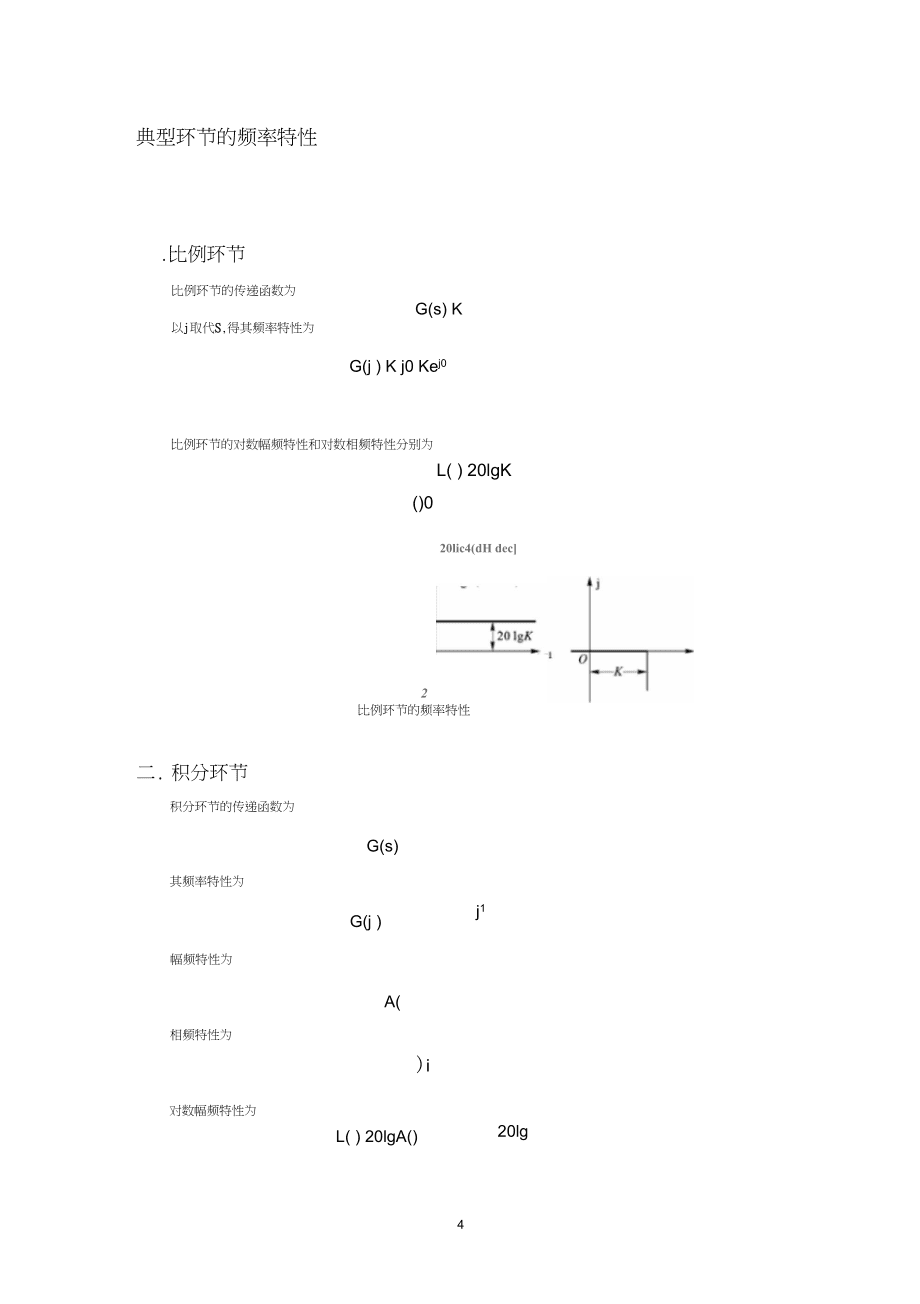
5、”。横坐标与幅频特性的对数相频特性的纵坐标表示相位移，是线性刻度，单位是“度” 横坐标相同。对数频率特性的坐标如图所示。JL30-专20-10-20-十倍预稈1十倍频程246102040 闕】00 皿圧“-30-图对数坐标典型环节的频率特性.比例环节比例环节的传递函数为G(s) K以j取代S,得其频率特性为G(j ) K j0 Kej0比例环节的对数幅频特性和对数相频特性分别为L( ) 20lgK()020lic4(dH dec2比例环节的频率特性二. 积分环节积分环节的传递函数为G(s)其频率特性为G(j )j1幅频特性为A(相频特性为对数幅频特性为L( ) 20lgA()20lg)i5图5

6、-8积分环节的幅相频率特性积分环节对数幅频特性是一条斜率为20dB/dec的直线，它在 =1这一点穿越零分贝线；相频特性与频率无关，在由0时，其为平行于横轴的一条直线。14三. 惯性环节惯性环节的传递函数为G(s)Ts 1其频率特性为G(j)Tj1、幅相频率特性幅频特性为A()1A (T )2相频特性为G(j )arcta nT四. 振荡环节振荡环节的传递函数为G(s)2 2T2s22 Ts 1式中，T为时间常数；Z为振荡环节的阻尼比（0< Z <1）。其频率特性为G（j）1T2 22 Tj振荡环节的对数幅频特性为L( ) 20lgA()20lgJ(1 T2 2)2 (2T )2在

7、低频段,T<<1（即 << 丄）时，LT）-20log1 = OdB。这是一条与横轴重合的直线,即低频渐近线。在咼频段，T>>1，即这说明高频渐进线是一条斜率为1>>-,L(T-40dB/ dec 的直线。) 20lgT 2 2 40lg(T )两条渐进线在=-=n点相交，故振荡系统的固有频率就是其转角频率。20-40.Ja"w£* 、J2Ole|C|/dB100-10-20-30010.1振荡环节的对数频率特性0ajJO五.微分环节微分环节的传递函数为其频率特性为对数幅频特性为G(s)G(jL()20lg A()20lg-I

8、tIDrii10微分环节的频率特性六.一阶微分环节其传递函数为频率特性为对数幅频特性为G(s) s 1G(jL( ) 20lgr7最小相位系统凡是在S右半平面上没有极、零点的系统，称为最小相位系统，否则称为非最小相位系 统。从频率特性的角度看，具有相同幅频特性的一些系统，可以有不同的相频特性，其中在 任意大于零的频率下，相位滞后都是最小的系统，称为最小相位系统。控制系统的开环对数频率特性一个复杂系统的开环传递函数G(s )往往由几个典型环节串联而成，即G(吊)=GiQ)G暑(S其频率特性为G(jG1(j )G2(j ) A1( )ej 1()a A( )ej ()Gn(j )ej 2()An(

9、 )ej n()式中A(Ai()A2()Ai(i()2(i()对数幅频特性为L()20lg A(20lg Ai(20lgA2()20lg Ai()Li( ) L2(Li(绘制系统的开环对数频率特性曲线(波德图)的步骤为：1) 把系统的开环传递函数化为标准形式一一典型环节的传递函数之积，并分析各环节。2) 求出各转角频率1,2,等等，并按大小将它们标在频率轴上。3) 在 =I处垂直向上量出幅值 201ogK(dB)，得到a点，这里K为开环放大系数。通 过a点画出L()的低频渐近线，其斜率为 -20 (dB/dec)。 数。4) / dec;5)6)这里为系统含有积分环节的个以后每遇到一个转角频率

10、，就改变一次渐近线斜率。遇到1+ T(j )+(Tj )2 1,斜率改变士 40dB/dec。 对渐近线进行修正，便可画出精确的对数幅频特性曲线 画出系统每个组成环节的对数相频特性曲线，然后将它们在各个相同频率下相加。遇到(l+Tj ) 1,斜率改变士 20dBL()。即得系统的开环对数相频特性曲线用频率特性分析系统的稳定性例：某系统的开环传递函数为03 =(i+r,sxi+ r,5) 绘其开环奈奎斯特曲线，并判别其闭环系统的稳定性。【解】该系统开环频率特性为G K 3 =( + "舊 TT 加 当血=0时， G*1忡)=K = K尹傑=K/O" 当afco 时，IiTn(7,(;e»> = Q 门值的Gk(j )值,上面这两个特殊点确定了奈氏曲线的变化趋势。再计算几个对应不同 便能绘制出如图当K增大时，Gk(j )曲线将成比例地向外扩张，但形状不变，并且不会包围(-1 , j0)点,已知开环传递函数中没有右极点。因此，该闭环系统总是稳定的。对数频率特性稳定判据【例】已知系统的开环传递函数为300G(s)H(s) s(s 2s 100)试用对数稳定判据判别系统的稳定性。【解】 绘制系统对数频率