212指数函数及其性质第1课时指数函数的图象及性质 (2)

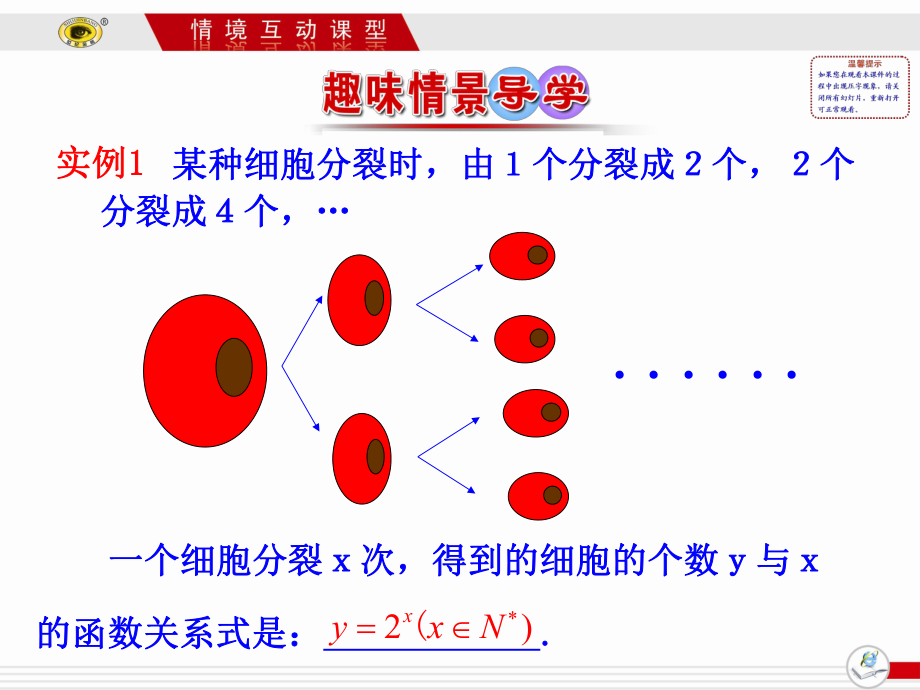
1、2.1.2 指数函数及其性质 第1课时 指数函数的图象及性质 一个细胞分裂次，得到的细胞的个数与一个细胞分裂次，得到的细胞的个数与的函数关系式是：的函数关系式是： . .2)(xyxN实例实例1 1 某种细胞分裂时，由个分裂成个，个某种细胞分裂时，由个分裂成个，个分裂成个，分裂成个， 庄子庄子逍遥游逍遥游记载：一尺之椎，日取其记载：一尺之椎，日取其半，万世不竭半，万世不竭. .意思是一尺长的木棒，一天截取一意思是一尺长的木棒，一天截取一半，很长时间也截取不完半，很长时间也截取不完. .这样的一个木棒截取这样的一个木棒截取x x次，剩余长度次，剩余长度y y与与x x的关系是的关系是 . 12)

2、（ ） (xxNy实例实例2 2这个式子是这个式子是怎么得出来怎么得出来的呢？的呢？截取截取次数次数木棒木棒剩余剩余1次次2次次3次次4次次x次次尺21尺41尺81尺161尺x)21()()21(*Nxyx实例实例1 1和实例和实例2 2涉及的函数有什么共同特点呢？涉及的函数有什么共同特点呢？接下来我们一起来探究这个问题接下来我们一起来探究这个问题. .1.1.理解指数函数的概念理解指数函数的概念 ； （重点）重点）2.2.掌握指数函数的图象和性质掌握指数函数的图象和性质 ； （重点、难点）重点、难点）3.3.培养学生实际应用函数的能力；培养学生实际应用函数的能力； 形如形如y=2y=2x x

3、， 的函数是指数函数的函数是指数函数. .那那么，指数函数是怎样定义的呢？么，指数函数是怎样定义的呢？12xy （ ） 一般地，函数一般地，函数_（a a，且，且aa）叫做指数函）叫做指数函数，其中数，其中x x是自变量，函数的定义域是是自变量，函数的定义域是_._.探究点探究点1 1y=ay=ax xR R指数函数的概念：指数函数的概念：思考：思考：在指数函数在指数函数y=ay=ax x中，为什么要规定中，为什么要规定a0,a0,且且 a1 a1呢？呢？提示：提示：若若a=0a=0， 若若a a0 0，比如，比如y=(-4)y=(-4)x x，这时对于，这时对于x= (x= (nNnN* *

4、) ) 在实数范围内函数值无意义在实数范围内函数值无意义. . 若若a=1a=1,y=1,y=1x x=1=1是一个常量，因此对它就没有研是一个常量，因此对它就没有研 究的必要，究的必要，xxx 0a0 x 0a当 时，恒等于，当 时，无意义12n为了避免上述各种情况，所以规定为了避免上述各种情况，所以规定a a0 0且且a1.a1.21yx（ ）；23xy （ ）；34xy （ ）；(4)3;xy 21(5).xyx. .（2 2）例例1 1 下列函数中是指数函数的函数序号是下列函数中是指数函数的函数序号是1xya 幂系数为幂系数为1 1底数为正数且底数为正数且不为不为1 1的常数的常数自变

5、量仅有自变量仅有这一种形式这一种形式例例2 2 已知指数函数已知指数函数 f(xf(x)=)=a ax x(a(a0,0,且且a a1)1) 的图象的图象经过点经过点(3,)(3,)，求，求f(0)f(0)，f(1)f(1)，f(-3)f(-3)的值的值. .解析：解析：指数函数的图象经过点指数函数的图象经过点(3,)(3,)，有，有f(3)=f(3)=，即即 a a3 3=， 解得解得于是于是13a x3f x 所以所以101331(0)1,(1),( 3)fff关键条件关键条件用用 描点法描点法 作出下列两组函数的图象，作出下列两组函数的图象，然后写出其一些性质：然后写出其一些性质：12x

6、y ()探究点探究点2 2 研究函数都会研究函数图象，如何画出研究函数都会研究函数图象，如何画出指数函数的图象呢？指数函数的图象呢？x x-2-2-1.5-1.5-1-1-0.5-0.50 00.50.51 11.51.52 2y=2y=2x x0.250.25 0.350.350.50.50.710.711 11.411.412 22.832.834 4描点法是作描点法是作函数图象的函数图象的通用方法哦通用方法哦2xy 011xy011xy12xy12（）xy x x-2-2-1.5-1.5-1-1-0.5-0.50 00.50.51 11.51.52 24 42.832.832 21.41

7、1.411 10.710.710.50.50.350.350.250.2512xy0.0370.110.3313927y=3-x279310.330.110.037y=3x3210-1-2-3x(2) (2) 与与 的图象的图象. . 列表：列表：3xy 1( )3xy 同坐标系中画出两函数图象，并观察图象的特点同坐标系中画出两函数图象，并观察图象的特点3xy011xy13xy关于关于y y轴对称轴对称都过定都过定点（点（1,01,0）3xy2xy 011xy12xy13xy关于关于y y轴对称轴对称都过定点都过定点（1,01,0）011xy12xy13xy2xy 3xy 011xyxy010

8、1xyy=ax (0a1)xy01xya(01)a01xya(1)a xy 图象共同特征：图象共同特征：（1 1）图象可向左、右两方无限伸展）图象可向左、右两方无限伸展（3 3）都经过坐标为（）都经过坐标为（0 0，1 1）的点）的点（2 2）图象都在）图象都在x x轴上方轴上方图象自左至右逐渐上升图象自左至右逐渐上升图象自左至右逐渐下降图象自左至右逐渐下降（2 2）在）在R R上是上是减函数减函数（1 1）过定点（）过定点（0 0，1 1），即），即x=0 x=0时，时，y=1y=1 性质性质（0 0，+） 值域值域R R定义定义域域图象图象a1a10a10a1探究点探究点3 3 由函数图象

9、可以得出函数的哪些性质呢？由函数图象可以得出函数的哪些性质呢？（2 2）在）在R R上是上是增函数增函数 01xya(1)a xyxy01xyaa a决定决定单调单调性性(0a1)【总结提升总结提升】指数函数图象和性质的巧记指数函数图象和性质的巧记(1)(1)指数函数图象的巧记方法指数函数图象的巧记方法: : 一定二近三单调一定二近三单调, , 两类单调正相反两类单调正相反. .(2)(2)指数函数性质的巧记方法指数函数性质的巧记方法: : 非奇非偶是单调非奇非偶是单调, , 性质不同因为性质不同因为a, a, 分清比分清比1 1大或小大或小, , 依靠图象记性质依靠图象记性质. . 2.53

10、0.10.20.33.11 1.7,1.7 ; 2 0.8, 0.8;3 1.7, 0.9.例例3.3.比较下列各题中两个值的大小比较下列各题中两个值的大小解：解：(1)(1)根据函数根据函数y=1.7y=1.7x x的性质，的性质，1.71.72.52.51.71.73 3. .(2)(2)根据函数根据函数y=0.8y=0.8x x的性质，的性质，0.80.8-0.1-0.10.81.71.70 0=1=1，根据函数根据函数y=0.9y=0.9x x的性质，的性质，0.90.93.13.10.90.90.93.13.1根据指数根据指数函数的性函数的性质质不同底的要找中间值不同底的要找中间值0

11、14（ ）3514（ ）230 19. 00 19.用用“”或或“”填空：填空：5643（ ）043（ ）745 06. 05 06.【变式练习变式练习】1.1.下列以下列以x x为自变量的函数中为自变量的函数中, ,是指数函数的是是指数函数的是( )( )2.( 4).2 4.(01)xxxxA yB yC yD yaaa 且B B2.2.若函数若函数y=y=（a a2 2-3a+3-3a+3）a ax x是指数函数，则（）是指数函数，则（）A Aa a1 1且且a1a1 B Ba=1a=1C Ca=1a=1或或a=2a=2 D Da=2a=2【解析解析】若函数若函数y=y=（a a2-3a

12、+3-3a+3）a ax是指数函数，是指数函数，则则a a2-3a+3=1-3a+3=1，解得解得a=2a=2或或a=1a=1，又因为指数函数的底数又因为指数函数的底数a a0 0且且a1a1，故故a=2.a=2.D D定义是考定义是考查的重点查的重点3.3.函数函数y=ay=ax-3+2+2（a a0 0且且a1a1）的图象一定经过点）的图象一定经过点P P，则，则P P点的坐标为（）点的坐标为（）A.A.（-2-2，-3-3） B.B.（3 3，3 3）C.C.（3 3，2 2） D.D.（-3-3，-2-2）【解析解析】因为因为y=ay=ax-3x-3+2+2（a a0 0且且a1a1）

13、，），所以当所以当x-3=0 x-3=0，即，即x=3x=3时，时，y=3y=3，所以函数所以函数y=ay=ax-3x-3+2+2（a a0 0且且a1a1）的图象过定点）的图象过定点P P（3 3，3 3）. .B B【解析解析】解法解法1 1, ,大于，且大于，且, ,大于小于大于小于且且4.4.如图如图, ,指数函数指数函数:A. :A. y= =ax x B.B.y= =bx x C.C.y= =cx x D. D. y= =dx x的图象的图象, ,则则a, ,b, ,c, ,d与与1 1的大小关系是的大小关系是_._. xyBDCAO结论：当结论：当a11时时, ,图象越靠近图象越靠近轴，底数越大轴，底数越大; ; 当当00a1d1abcd1abxyBDCAO1.E.F.G.H5.5.已知指数函数已知指数函数f f（x x）的图象过点（）的图象过点（3 3，8 8），），求求f f（6 6）的值）的值【解析解析】设指数函数为：设指数函数为：f f（x x）= =a ax x(a(a00且且a a1)1)，因为指数函数因为指数函数f f（x x）的图象过点（）的图象过点（3 3，8 8），），所以所以8=a8=a3 3，所以，所以a=2a=2，所以所以f f（x x）=2=2x