石砌二平铰拱桥的计算

1、石砌二平铰拱桥的计算省拱桥研究报告之二湖南省交通规划勘察设计院拱桥研究小组（上官兴执笔）在设计石肋双曲拱和石砌版肋拱桥中，常常出现拱止上缘拉应力大于圬工容许的拉应力情况。按“桥规”，在偏心距不超过规定时，可保持拱趾受力状态不变，考虑材料的塑性进行“应力重分布”计算。这样虽然可设计边缘应力不于允许压应力值，但是拱趾截面上缘既在已经开裂，因此，拱趾固结条件就得不到保证。在超静定结构中，支承条件改变将引起内力的重分配，即拱趾的无铰拱弯矩值M无随着裂缝的产生而相应消失。部交研院和江苏、无锡交通局在资料1中所提出的“平铰”概念，从理论上解释了无铰拱拱趾微小转动进入平铰状态后，能使固端弯矩有所放松，因之对

2、温差、砼收缩、弹性压缩和支座位移有较好的适应性。“平铰拱”计算理论，突破了无铰找的框框，使圬工拱桥得到了进一步的发展。本文系在学习国内有关“平铰拱”的一系列科研成果基础上，结合我省石砌圬工拱桥的实践提出的，是“平铰拱”计算的另一种方法。其特点是以双铰拱为基本体系，再迭加两拱趾平铰端面上的轴向力偏心弯矩WK而成。这样“平铰”与理论双铰相比较，多了WK的约束，致使拱顶活载弯矩有所减少，与无铰拱比较又有致在拱趾拱圈有相对位移时出现过大的负弯矩。特别是在石砌版肋拱当中性轴偏下，上缘拉应力大时，就“运用”平多拱理论可解决。现以L=40m，f/L=1/8的黄岩冲石砌版肋拱桥为例进行分析说明。由于水平所限，

3、错谬难免，欢迎批评指正。一、二平铰的计算图示本节从分析平多的特性提出平铰拱的计算图式。（一）平铰特性：1、平铰构造：“平铰”系指拱圈拱趾和桥墩（台）的拱座间设有平缝。缝中一落千丈般涂有石蜡、机油或沥青等润滑材料。对于那些用砂浆砌筑，以后自然开裂成缝者，也称“平铰”。“平铰”相当于一个半径为的铰。与理论铰比较，平铰不能自由转动，即在转动中要受到一定程度的约束。与结构中（固结）相较，平铰不能承受拉应力，所以能承担的弯矩有限。2、平衡条件：二平铰拱在外荷作用下，拱趾将产生微小的转动，转角为。由于铰面平缝，故仅以偏心压京戏力的形式满足平衡条件。如图1平铰转动上缘开裂，下缘产生压缩变形和压应力。3、平铰

4、拱转换：在图1中轴向力N与压应力相平衡后且N作用在受压区高度h的重心上。设重心距下缘距离为C，则偏心距e可由下式求得：e下=X下-C式（1）。将轴向力N移至截面形心轴上，铰端上的附加约束弯矩WK=-Ne式（2）。则与原平铰偏心压应力状态是等效的。由此，看出平铰拱的结构特性是可以以双铰拱为基本结构，再迭加两拱趾铰面轴向力N偏心弯矩WK来表示其受力图式。(二）计算图式1、据平铰拱行性分析，其计算图式可表示：平铰拱=双铰拱+WK 式（3）2、现以P=70T作用在5#截面上，拱趾水平位移0=-15.425*10-6(m)的情况为例说明平铰拱图式的特点如图2。二、双铰拱计算如前所叙，平铰拱计算系以双铰拱

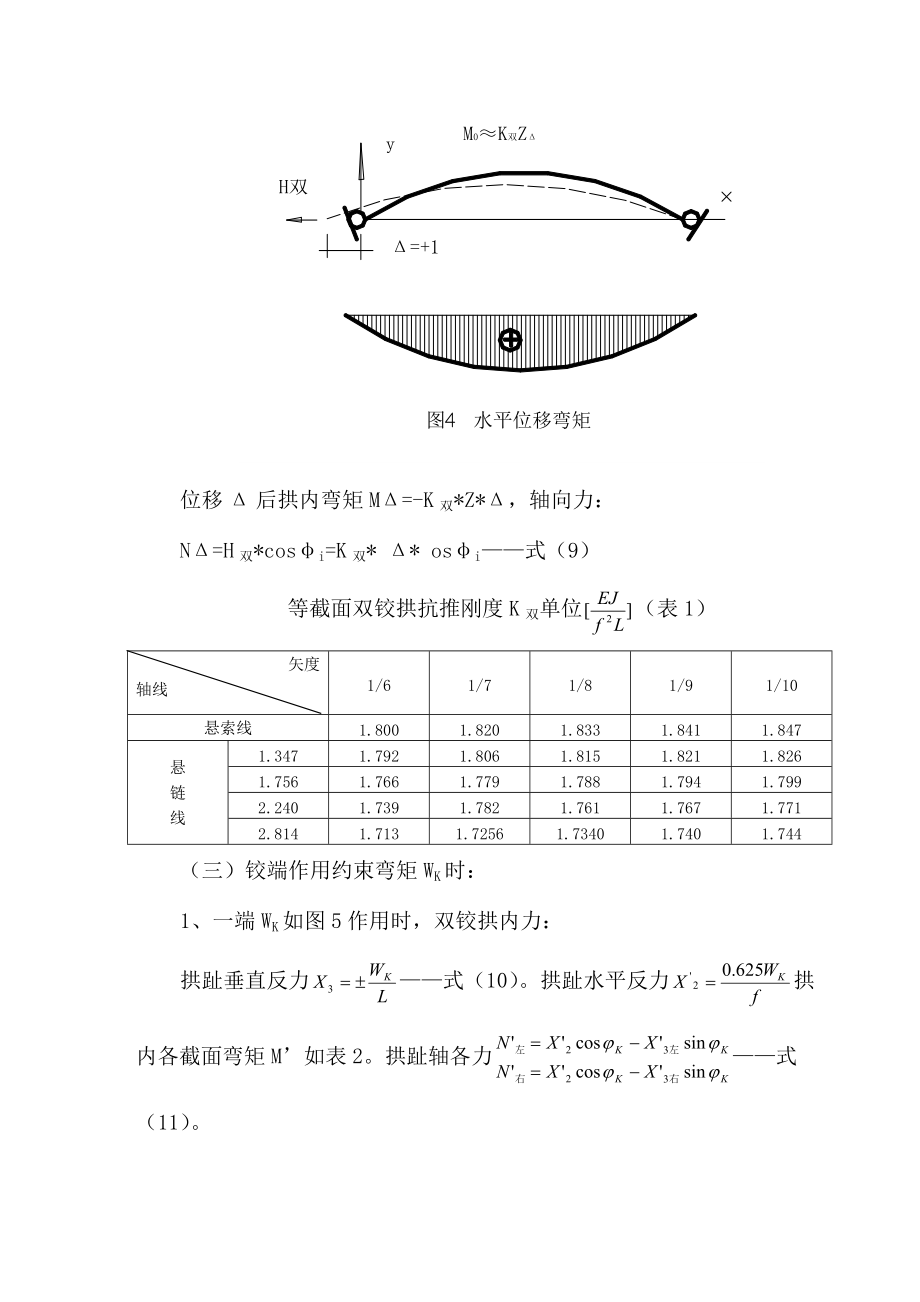
5、为基本体系，因此本节简要地介绍双铰拱一般计算公式。有关计算用表可参阅资料3和4。（一）垂直荷载P如图3。1、拱趾垂直反力：式（4）2、简支梁弯矩M0：式（5）3、推力H双影响线可在资料3和4中查得。4、双铰拱弯矩M双=M0-HZ0式（6）（二）水平位移如图4当双铰拱拱趾产生向外的相对分离水平位移=1时，所需要水平拉力称抗推刚度K双，一般可由单位水平力作用拱趾产生的水平位称22反算，即式（8）。常用K双值如表1。位移后拱内弯矩M=-K双*Z*，轴向力：N=H双*cosi=K双* * osi式（9）等截面双铰拱抗推刚度K双单位（表1）矢度轴线1/61/71/81/91/10悬索线1.8001.82

6、01.8331.8411.847悬链线1.3471.7921.8061.8151.8211.8261.7561.7661.7791.7881.7941.7992.2401.7391.7821.7611.7671.7712.8141.7131.72561.73401.7401.744（三）铰端作用约束弯矩WK时：1、一端WK如图5作用时，双铰拱内力：拱趾垂直反力式（10）。拱趾水平反力拱内各截面弯矩M如表2。拱趾轴各力式（11）。2、两端作用相等WK如图6，此时无垂直反力，水平力拱内各截面弯矩M见表2。轴向力N=X2cosK式（12）。3、左右两端W左、W右不等且同时作用时，可分别算出一端WK作

7、用时的内力，再迭加而成。（四）初始水平位移O为了简化计算，可以将拱轴向力所产生的弹性压缩、温降、砼徐变等因素合并换算为拱趾产生初始水平位移O，现以黄岩冲桥计算来说明。1、弹性压缩：可将拱轴展直成弧长S，相当在其上作用水平推力Hg所引起的拱圈在水平面方向的缩短u。式（13）2、温降t=-30,所引起的拱圈在水平面方向上的缩短式（14）。式中为材料线胀系数，L为跨径，也可理解为桥台氧生的水平位移9.67mm。t=8*10-6*(-30)*40.2958=-9.670*10-3(m)。3、初始位移O=u+t 式（15）O=u+t =-（5.755+9.670）*10-3=-15.425*10-3(m

8、)4、O=-15.425*10-3(m)在双铰拱中产生内力计算。抗推刚度K双117.3EJ/L3=117.3*4.50=0.527*103(T/m)位移的推力H双=K双*=0.527*(-15.425*10-3)=-8.139(T)拱顶弯矩Mi2=H双*f=(-8.139)*5.035=40.984(T-m)5#截面弯矩M5=-H双*Z5=-（-8.139）*3.344=27.22(T-m)拱趾轴向力N=H双*cosK=(-8.139)*0.8908=-7.25(T)（五）黄岩冲桥双铰拱内力和挠度1、计算资料：净跨L0=40M，f/L=1/8悬索线拱轴，主拱圈采用125#砂浆砌1000#方块石

9、（粗料石锒面）。允许应力=（590+690）/2=640（T/m2）弹性模量E=1.45*800K=1.45*800*2.5*640=1.856*106(T/m2)式中1.45系石料厚度的提高系数。截面惯性矩J=0.1586(m4)面积F=2.63(m2)主拱宽B=5m。平均厚度计算跨径l=40.296(m),矢高f=5.035(m)弹性抗力系数的K=E/m=1.856*106(T/m3)抗转动刚度KJ=0.2944*106（T-m）抗弯刚度：EJ=0.2944*106（T-m2） 2、单位荷载产生的挠度、内力如表340M版肋拱单位荷载的挠度、内力（表3）荷载项目挠度（mm）f5-0.0530

10、.040-0.0130.962f120.01520.01520.03041.555f50.040-0.053-0.0130.962弯矩M（T-m）M0-10-10M5-0.3750.208-0.1671765弯矩M（T-m）M120.1270.1270.2542657M50.208-0.375-0.1671765M00-1.00-10轴向力NN左K-0.0996-0.1222-0.2218-470拱顶-0.1245-0.1245-0.249-527.7N右K-0.1222-0.0996-0.2218-4703、荷载P和位移及恒载G在双铰拱中内力、挠度如表4。三、平铰拱轴向力偏心弯矩WK由图1平

11、铰转动后压应力平衡条件可见，铰面轴向力N的偏心弯矩WK=N*C。大小平铰转动角密切相关。本节从分析值出发，提出计算WK的公式。（一）无铰拱拱趾为固结端，在外荷作用下用常规方法可求得弯矩M和轴向力N。在N作用下，全截面受压，在弯矩M作用下，上（下）缘产生拉（压）变形，按弹性理论截面假定可知上（下）缘变形后的连线是直线与原截面法线的夹角称转角无如图7。40M版肋拱荷载作用下的挠度、内力（表4）截面0#5#12#5#0#项目挠度f(mm)P=30T拱顶0-1.503.00-1.500P=70T(5#)0-16.18-2.8019.340=-15.425mm014.83823.98614.8380弯矩

12、M（T-m）恒载(-23.05)28.87-27.3120.87(-23.05)P=30T拱顶(34.58)-27.5741.13-27.57(34.58)P=70T(5#)(89.4)-96.3-35.0177.7(-149.2)=-15.425mm(-156.84)27.2240.98427.22(-156.84)轴向力N（T）恒载748670748P=30T拱顶47.7045.947.70P=70T(5#)64.6265.1083.16=-15.425mm-7.25-8.14-7.25注：（弯矩）是拱趾无铰拱的弯矩M无值，其功用详见下节。2、参照弹性地基梁的概念，令k是主拱圈材料的弹性抗

13、力系数，即表示为当拱圈产生单位压缩变形=1时，拱座给拱圈的抗夺压应力，这样拱圈上下缘的应力可表示为：=k*式（16）。弯矩M无作用下的应力又可以用截面的几何要素来求得，即：式（17）。由于转角很小，式（18）。弯矩作用下的边缘变形上=*X上，下=*X下将以上三式联解，可求得无铰拱的拱趾关系式：转角： 弯矩：式（19）即：转角等于弯矩除以抗转刚度kJ，弯矩等于转角无乘以抗转刚度kJ。3、由于轴向力N使全截面纤维均匀受压，不产生转角，所以N和M无共同作用所产生的上下缘纤维转角无与仅有弯矩M无作用时相同。由于应力是变形的K倍，因此图7中上下缘应力联线的夹角也是无，即：拱趾上下缘的变形和应力联线的夹角

14、都等于拱趾的转角无。当上缘出现了拉应力时，转角仍符合式（19）关系式。这里应指出，所谓无铰拱的“固结”并不等于没有转角，只不过上下缘纤维转角值无很小而已。在无铰拱计算中，一般不计算无，而仅要求拱趾设置钢筋来承担弯矩所产生的拉应力而已。而平多拱恰好就利用了这个微量的转动，以允许上缘一定程度的裂缝，来降低固结端的刚度。4、拱圈材料的弹性抗力系数K（T/m3），据资料1的模型试验分析求得。即与材料 弹性模量E成比例，再除以长度单位（m）的关系。但这里面包含了部分塑性，如果剔除塑性，按纯弹性考虑可假定k=E/m式（20）。不同材料精确的k值，尚有进一步实验求得。应当指出k是个比例值，其绝对值大小只影响

15、应力值而对平铰面轴向力偏心弯矩W影响不大。（二）平铰拱拱趾转角平1、资料1的平铰模型试验分析指出，平铰拱在受荷后铰面所产生的微小边转动角度平是由两部份组成，如图8。平=无+ 无式（21）式中无是由全拱的物理性质所决定的，如前式（19）等于，因此可利用现有的无铰拱拱趾弯矩M无表格来反求。例如表5列出水平位称及垂直荷载P作用下转角。2、是由于拱圈拱趾转动后下缘局部受压应力大于全截面工作时的应力而产生的附加压缩量所相应的纤维夹角大小。据资料1的模型试验分析，值的影响范围为1.5-2D长度内（D为截面全高）这和预应力锚头处应力集中沿轴线逐渐递减的规律相同的。由于大区间内受力十分复杂，故值计算很困难，但

16、实验所测值不大，随跨径上面相对小。因此为了简化计算可忽略，故平=无+ 无即平铰拱的转角与无铰拱上（下）缘纤维的夹角值相近。应当指出考虑圬工材料的塑性后，能减少转角平的计算值，所以假定0-无所少读计的可以部份地为塑性所少算的平值来补偿，这方法是完全可以满足用于生产上要求的。（三）轴向力N偏心距e1、矩形截面如图9平铰转角平=/h下缘应力=E*=E*h*轴各力N距下缘高度C=h/3根据轴向力N与压应力相平衡条件可得：N=1/2*h*B*=1/2*h*B*k*h*受压区高度式（22）由式可见，h与k值大小无关。偏心矩e=X下-C=X下-h/3式（23）2、非线性截面可用逆算法作曲线图求得，如图10。

17、黄岩冲桥工型截面，假定受压区高度h=0.625m。计算求得受压区高度h范围内面积F=2.19(m2)Y下=0.2378(m) Y下=0.3872(m)惯性矩：J=54.96*10-3(m4)截面模量W上=J/ Y下=54.96*10-3/0.3872=0.142(m2)h=0.625(m)处应力式（24） 即轴向力N作用在距中性轴上处。N与下缘高度C=Y下-上=0.173（m）全截面中性轴X下=0.3256(m) X上=0.5744(m)轴向力N由式（24）可知（式中：，）令系数：式（25）同理可计出h=0.15、0.35、0.90时的偏心距e，面积F和系数值，如表6所列，将表6结果绘成图12

18、，当计算=N/大于2.8038*106则表明全截面受压。截面-e、F、Z关系（表6）项中性轴（m）核心半径(m)受压区面积F(m2)倍数=N/偏心距e(m)HY上Y下0.150.0750.0750.0250.750.1044*1060.27560.350.1750.1750.05831.750.5684*1060.20890.6250.38720.23870.06482.191.5738*1060.15260.900.57440.32560.10502.632.8038*1060.1050(四)轴各力N偏心距WK如图111、W=-N*e e由=N/查曲线求得，图12轴向力N=N双+N水平力H=

19、H双+ X2 式（26）垂直力V=V双+ Z3”式中N、 H、 V是偏心距WK在双铰拱拱趾产生的反力:N=X2cosK , V=Z3”sinK。在WK未求得是未知的，因此需要采用“渐近法”求解。2、计算步骤如下，具体方法见下节例题。先假定W左，算出N左和N”右：假定W右，算出N右和N”左。计算N左=N双+N左+N”右和=N/N右=N双+N”左+N右式（27）在-e关系曲线上查得相应e，则W左=N左*e，W右=N右*e。将W与原假定相较，不符处再假定重算，直到接近为止。3、对称荷载，两拱趾WK相同，则无垂反力N=XcosK，当跨径较大Z3值很小时，也可近似忽略不计垂直力Z3的影响。4、计算中如=

20、N/2.8038*106时，铰端弯矩W等于无铰拱值，即W=kJ。将试算求出的两拱趾W左，W右按表2数值，求出各截面内力，（M和N）再与原双铰拱内力（M双，N双）选加得出平铰拱内力。5、WK的特性。如令两拱中WK=0则为双铰拱，如令WK=EJ=M无（即等于无铰拱拱趾弯矩）再迭加在双铰拱上，所求得的平铰拱内力实质上等于无铰拱内力。这恰好是本文方法的特点所在。由此不难理解，无铰拱是拱趾未开裂，铰端约束弯矩WK=M无的双铰拱是拱趾能自由转动，无约束弯矩者（WK=0）平铰拱则介于两者之间，由转角大小和轴向力N不同的偏心程度使铰端存在着部份约束弯矩，因此平铰具有无铰双铰两者的部份性能。平铰拱的铰以简单的平

21、缝来代替复杂的铰结构，其受力特性又优于理论双铰，这在我国桥梁实践中有一定的实用价值。四、固定拱计算现以考虑弹性、温降，相当支座位移O=-15.425*10-3(m)时拱顶加载30T和截面加载70T两种情况说明平铰拱的计算方法，步骤及其特性。（一）拱顶加载P=30T如图1。1、拱趾双铰拱反力如表7表7内力项目轴向力N转角=1、恒载G=334T748(T)78.3*10-62、活载P=30T47.7(T)-117.5*10-63、支座位移-15.425*10-3(m)-7.3(T)532.7*10-6双铰拱788.4(T)493.4*10-6(弧度)首先假定WK=M无=-EJ(无铰拱)=-0.29

22、44*10-6*493.4*10-6=-145.26(T-m)W引起的轴力N=0.2218 WK=-32.2(T)拱趾总轴力N=N双+N=788.4-32.2=756.2(T)系数=N/=756.2/(493.4*10-6)=1.5326*106在图12上查得偏心距e=0.155(m)故平铰弯矩W=-Ne=-756.2*0.155=-117.211(T)与假定不符，重新计算。2、再假定首先假定WK= -117.211(T-m)N=-0.2218* 117.211=-25.994N=788.4-26.00=762.4=N/=762.4/(493.4*10-6)=1.545查曲线得e=0.154(

23、m)Wk=-Ne=-762.4*0.154=-117.4(T)与原假定-117.2基本相等。3、将两拱趾同时作用WK= -117.2 (T-m)，按表3单位力数求出双铰拱内力及挠度如下：挠度：f5=f5=-0.013*117.2=-1.5236(mm)f12=0.0304*117.2=3.529(mm)弯矩：M5=M5=-0.167*117.2=-19.57(T-m)M12=0.254*117.2=29.769(T-m)轴力：N5=N5=-0.2218*117.2=-26T-m)N12=-0.249*117.2=-29.18(T-m)4、平铰拱挠度及内力计算如表8表8截面项目0#5#12#5#

24、0#挠度f(mm)双铰拱P=30T0-1.5003.000-1.5000=-15.425014.83823.98614.8380合计013.33826.98613.3380WK=-117.20-1.5243.563-1.5240平铰拱011.81430.54911.8140弯矩M（T-m）双铰拱G=334T028.87-27.3128.870P=30T0-27.5741.31-27.570=-15.425027.2240.98427.220合计028.5254.80428.520WK=-117.2-117.2-19.5729.769-19.57-117.2平铰拱-117.28.9584.573

25、8.95-117.2将表8的结果绘成图14并与双铰拱，无铰拱比较如下：平铰拱较无铰拱弯矩折减19%，拱顶弯矩折减8%，而5#截面弯矩增大，但绝对值较小，不控制设计，拱趾挠度小3%。平铰拱与双铰拱相较，拱趾弯矩增大54%，挠度增大13%。总之，由于P=30T作用拱顶使拱趾产生正弯矩与=-15.425(mm)使拱趾产生负弯矩相反，故拱趾平铰转角不大，开裂不长基本上仍接近无铰拱。但由于平铰拱趾WK较约束减少，因此对适应水平位移而言又比无铰拱为好。 （二）5#截面加载70T如图151、拱趾双铰拱反力如表9表9截面荷载左拱趾右拱趾N左（T）左（弧度）N右（T）右（弧度）1、恒载G=334T74878.3

26、*10-674878.3*10-62、活载P=70T64.62-304*10-683.16506.8*10-63、位移=-15.425(mm)-7.3532.7*10-6-7.3532.7*10-6双铰拱805307*10-68241118*10-6先假定W左=-EJQ左=-90.4=M无 W右=EJQ右=-90.4=M无W左 N=-0.0996*90.4=-9 N”=-0.1222*90.4=-11W右 N”=-0.1222*329=-40.2 N=-0.0996*329=-32.8N左=755.8 N右=780.2=755.8/（307*10-6）=2.416*106 =780.2/（11

27、18*10-6）=0.697*106查图：e=0.119 e=0.202W左=-Ne=-89.94 W右=-157.6再假定W左=-89.7 W右=-160W左产生：N=-8.93 N”=-10.96W右产生：N”=-19.55 N=-15.94N=N双+ N+ N” N左=776.52 N右=797.1 =N/ =2.53 =0.713查图12 e=0.1155 e=0.201W=-Ne W左=-89.68-89.7 W右=-160.2(T-m) -1603、将试算求得的W左=-89.68和W右=-160.2乘以表3的单位值，得到表10WK在双铰拱上挠度及内力。再与双铰拱P、值相加，如表11

28、求出平铰拱挠度和内力。将表11数值绘成图16，由图知，当平铰拱作用不对称荷载P和位移时有如下情况:荷载P作用下平铰拱与无铰拱相比，5#截面弯矩要大49%，挠度大44%。这与荷载P作用在拱顶时是不同的。与双铰拱相较，5#截面弯矩减少18%，挠度减少14%，这与P在拱顶时情况相反。平铰拱左拱趾弯距与无铰拱值基本接近。而右拱趾由于靠近P，产生活载负弯矩和位移=-15.425mm，使负弯矩总值达到M=-329（T-m）。平铰拱上缘拉开，放松约束使弯矩折减51%，M平=160(T-m)，由W右减少使平铰M5无铰M5的主要原因。平铰拱正负弯矩的绝对值比较接近 ，而双铰、无铰的弯矩绝对值 均大于平铰拱，这说

29、明平铰拱受力较为均匀。平铰拱能减少右拱趾弯矩，但却相应增大了5#截面正弯矩，说明要挖掘潜力，减少弯矩还必须进一步考虑拱上构造联合作用。拱趾W在双铰中挠度、弯矩（表10）截面项目0#5#12#5#0#平铰拱W左=-89.70-4.7541.3633.5880W右=-16006.4003.432-8.4800W平01.6463.795-4.8920无铰拱W左=-90.40-4.7911.3743.6160W右=-329013.165.001-17.4370M无08.3696.375-13.8210平铰拱W左=-89.7-89.7-33.63711.39218.6570W右=-160033.2802

30、0.32-60.0-160W平-89.7-0.35731.712-41.343-160无铰拱W左=-90.4-90.4-33.9011.4818.8030W右=-329068.4341.78-123.37-329M无-90.434.5353.26-104.567-329注：相当无铰的弯矩M无=-KJ；平铰拱拱趾弯矩W=-Ne。P=70T和=-15.425挠度、弯矩（表11）截面项目0#5#12#5#0#挠度f(mm)双铰拱P=70T016.182.8019.340=-15.425mm014.83823.98614.8380f双0-1.34221.18634.1780平铰拱01.6463.795

31、-4.8920f平00.30424.98129.2860无铰拱08.3696.375-13.8210f无07.02727.56120.3570弯矩M（T-m）双铰拱G=334T028.87-27.328.870P=70T0-96.3-35.0177.70=-15.425mm027.2240.9827.220M双0-40.2-21.3233.80平铰拱-89.7-0.35731.712-41.343-160M平-89.7-40.610.4192.5-160无铰拱-90.434.5353.26-104.6-329M无-90.4-731.9129.2-329五、连拱计算目前在平铰拱连拱计算中，一般均

32、以双铰拱的抗推刚度K双来代替抗推刚度。资料5公田大桥（9-16m）支载实验表明用此种方法所计算的桥墩位移比实测的大2.3倍，拱顶下缘拉应力比实测大5-6倍。通过对公田大桥实验分析，采用本文方法用初始位移0时平铰拱的抗推刚度K0来参入连拱计算，能大致符合实际。本节介绍平铰连拱方法计算的步骤和连拱中平铰特性。（一）0=-15.425mm时抗推刚度K平。如前所叙，黄岩冲桥考虑弹压，温降后相当拱趾产生了初始水平位移=-15.425*10-3（m），再按其恒载考虑拱轴线与压力线的偏离，腹拱推力Q作用等因素所得恒载无铰拱弯矩M恒=-23.05(T-m)如图17试算平铰状态内力。 1、转角=611*10-6

33、将恒载弯矩M无=-23.05(T)换成恒载转角。单位水平位移所产生的转角可由表5查得。初始水平位移=-15.425*10-3（m）所产生的转角总初始转角0=恒+0=（78+533）*10-6=611*10-62、假定WK=-125（T-m）（经试算得）X2=0.249WK=31.12(T)N=0.2218 WK =-27.7(T)N双=748-7.3=741(T)N= N双+ N=712.3=N/=712.3/(611*10-6)=1.165查图12得偏心距e=0.175W=-N/=-124.7与假定W=-125基本相符故可。3、抗推刚度K平系单位水平位移所需要的推力H大小。位移=-15.42

34、5*10-6时，双铰拱推力H双=-8.14(T), WK=-125(T-m)所产生的附加推力X2=31.12(T)，故平铰拱此时推力H平=H双+X2H平=-（8.14+31.12）=-39.26(T)故平铰刚度K平0= H平/=-39.26/(-15.425*10-6)=2.545*103(T/m)应当指出，K平=2.545*103(T/m)中包括了恒载偏离弯矩M=-23.05(T)的所产生的推力Z2=-5.739(T)在内，如果扣除则得平铰刚度：K平0=（39.26-5.739）/(-15.425*10-6)=2.17*103(T-m)(二)恒载水平位移时平铰特性用前叙同样方法，可计算不同水

35、平位移时，平铰拱的拱顶，拱趾弯矩和双铰比较如表12及图18。由图知，对于水平位移而言平铰拱有如下特性：1、当-5.28mm时，轴向力产生的压应力大于弯矩所产生的拉应力，拱趾未开裂，因此平铰拱与无铰拱的性质相同，即M无和MK等于无铰拱值。2、随着位移的增加，拱趾平铰转角加，拱趾上缘逐渐张开，轴向力的偏心弯矩WK=-Ne与无铰拱M无相较，折减系数=M平/M无愈来愈大，趋近于双铰拱M双。3、拱顶弯矩平铰拱小于无铰拱，但大于双铰拱。从理论上解释了资料1所实测的现象。这现象是由于一对WK作用在拱趾，必然在拱顶上产生正弯矩。W=-0.254WK，使M平=M双+M。必然大于M双。4、随着加大拱趾受压区高度h

36、减小，使应力集中于下缘，但版肋拱上截面下缘有全宽5m，对局部承压很有利，因此说工型截面是采用平铰拱的一种好型式。5、随着位移增大平铰拱拱顶MS和拱趾MK的增量不是常数，数值逐渐减小，然后趋近双铰拱值见表12。恒载位移平铰弯矩比较（表12）截面拱式位移0（mm）序号拱恒弯矩MS拱趾受压抗推刚度区高度K平*103拱趾弯矩MK(T-m)双铰平铰无铰h(m)T/m平铰无铰1- 5.2814.6034.0834.080.904.145-76.75-76.752-7.0018.5841.3842.500.773.732-90.10-94.213-9.0023.9249.7453.060.673.341-1

37、01.70-114.54-15.42540.9872.7186.660.522.545-125-179.95-20.0053.1287.12110.600.452.195-133.96-226.46-30.0079.77116.32162.980.371.725-144.26-328.07-40.00106.28144.9215.300.301.331-152.10-429.7（三）连拱计算中抗推刚度选择1、将表12中平铰拱抗推刚度K平绘成图19，由图可知平铰抗推刚度K平有如下性质：随着位移的加大而降低，最后趋近于双铰拱f双=-0.5277*103(T/m) 。当位移-5.28mm时与无铰刚度

38、K无=3.06*103相同，K平值是随拱圈位移变化的一个变数。这与双、无锵拱K值是个常数，有着明显的不同。由于平铰不遵循力的叠加原则，故恒载考虑拱轴压力线偏离后，在拱趾所产生的M0对K平有影响。即由K平提高到K平，在实际计算中对平铰而言，产生单位水平位移所需的推力，K平中已包括了M0的影响，故使用K平则不必再计算M0。2、在连拱计算中，因桥墩位移使拱圈产生的活载水平位移P，故主拱圈总水平位移=0+P，其抗推刚度和内力计算必须以值来计算。如图19中，如以初始位移u=-15.425*10-3(m)为原点座标，则相邻两拱圈，因桥墩位移P=-5mm，一孔受拉，一孔受压，其平铰刚度如图20。分别为K-=

39、2*103(T/m)K+=3.1*103(T/m)其平均值近似等于初始位移刚度:K平0=2.545*103(T/m)。因此为简化计算，在计算桥墩位移时，可近拟取各拱圈抗推刚度K拱= K平0，即不考虑刚度随水平位移而变化的影响。3、应当指出，求得=0+P后进行平铰内力计算时不应当采用K平0值来反算双铰连拱推力H平而应如前节一样值重新计算H平，这样精度更高些。总之，在连拱计算中平铰拱可近拟取初始状态的抗推刚度K平0来计算桥墩位移和拱圈=0+P。（四）拱顶加载P=30T连拱计算如图211、取拱圈初始抗推刚度K平=2.545*103(T/m)=K拱，比双铰拱K双=0.5277*103大4.8倍。桥墩抗

40、推刚度节点1抗推刚度K=2K拱+K墩=（2*2.545+4.091）*103=9.180*103（T/m） 桥墩水平位移，P=-45.9/（9.180*103）=-5.00（mm）荷载孔计算水平位移=0+P=-（15.425+5）=-20.425*10-3(m)2、如拱圈按双铰拱计算桥墩位称=8.92(mm) 比按平铰拱计大两倍多，随着桥墩刚度变小则按平铰K平计算的桥墩变位P将比双铰拱更少得多。荷载孔的计算位移=0+P=-（15.425+8.92）=-24.345*10-3(m)3、如拱圈按无铰拱计算桥墩位移=-4.491*10-3荷载孔计算位移=-（15.425+4.491）*10-3=-1

41、9.916*10-3(m)4、将上叙三种情况的连拱内力用前面方法同样计算，得出结果绘图22，由图可见，平铰拱考虑连拱后总弯矩，与双、无铰拱比较：拱顶小于无铰拱11%，大于双铰拱30%。拱趾小于无铰拱30%。5#截面小于双铰拱66%。总之，弯矩介于双、无铰拱之间，但更接近于无铰拱，拱趾和拱顶控制截面又比无铰拱弯矩减少11-30%，这就是平铰拱在连拱中适应方面优异无铰所在。应当说明由于孔数少桥墩刚度较大连拱作用还不显著，所以平铰比双铰的弯矩还是大一些，即适应位移不如双铰。附录：连拱计算比较1、平铰拱荷载孔内力：计算水平位移=-20.425*10-3(m)拱趾转角=（78.3-117.5）*10-6

42、+20.425*10-3*-0.03453=666*10-6拱趾轴力N双=748+47.7-(0.5277*103*20.425*10-3)/(-10.78)=785T假定WK=-134N=0.2218WK=-29.72N= N双+ N=755.27=N/=1.134查图12得e=0.177WK-Ne=-133.7(T-m)与假定的W=134相符。表13连拱M12=0.254WK=34(T-m)M双12=10.78*5.035=54.3(T-m)M5=-0.167WK=22.4M双5=-10.78*3.344=36.05恒活M平12=-27.31M12=41.13M平5=28.87M5=-27.57合计M12=102(T-m)M5=14.95(T-m)2、双铰拱荷载孔内力：=0+P=-（15.425+8.92）=-24.345*10-3(m)H双=-0.5277*103*