高频第5章频谱的线性搬移电路

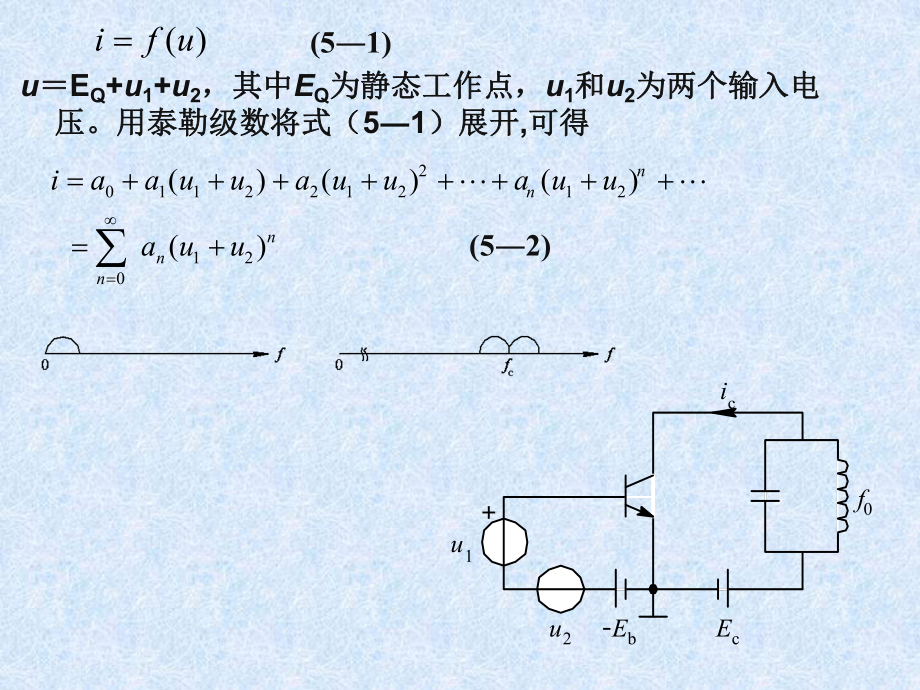
1、第5章 频谱的线性搬移电路 5.1 非线性电路的分析方法非线性电路的分析方法 5.2 二极管电路二极管电路 5.3 差分对电路差分对电路 5.4 其它频谱线性搬移电路其它频谱线性搬移电路5.1 非线性电路的分析方法 图图51 频谱搬移电路频谱搬移电路（a）频谱的线性搬移）频谱的线性搬移;（b）频谱的非线性搬移）频谱的非线性搬移 0f(a)0ffc0f(b)0ffc 5.1.1 非线性函数的级数展开分析法非线性函数的级数展开分析法 非线性器件的伏安特性非线性器件的伏安特性,可用下面的非线性函数来表示可用下面的非线性函数来表示: 式中式中, u为加在非线性器件上的电压。一般情况下为加在非线性器件上

2、的电压。一般情况下, uEQ+u1+u2，其中，其中EQ为静态工作点，为静态工作点，u1和和u2为两个输入电压。为两个输入电压。( )if u(51) EbEcu2u1f0icuEQ+u1+u2，其中，其中EQ为静态工作点，为静态工作点，u1和和u2为两个输入电为两个输入电压。用泰勒级数将式（压。用泰勒级数将式（51）展开）展开,可得可得( )if u(51)2011221212120()()()()nnnnniaa uua uua uua uu(52) EbEcu2u1f0ic 式中式中,an（n=0,1,2,）为各次方项的系数）为各次方项的系数,由下式确定由下式确定:(53) (54)(5

3、5) 式中，式中，Cmn=n!/m!(n-m)! 为二项式系数为二项式系数,故故 2011221212120()()()()nnnnniaa uua uua uua uu(52) )(!1)(!1Q)(QEfnduufdnanEunnnnmmmnmnnuuCuu02121)(nmmmnmnnnuuCai0210 先来分析一种最简单的情况。令先来分析一种最简单的情况。令u2=0,即只有即只有一个输入信号一个输入信号,且令且令u1U1cos1t,代入式（代入式（52）,有有(56) (57) 110cosnnnibUnt(58) 01101cosnnnnnnntUauai )2cos(21 )2c

4、os(21cos)1(21011202/为奇数为偶数nxknCnxknCCxnkknnnkknnnnn图图52 非线性电路完成频谱的搬移非线性电路完成频谱的搬移 非线性器 件滤波器u1uou2 若作用在非线性器件上的两个电压均为余弦信号若作用在非线性器件上的两个电压均为余弦信号,即即u1U1cos1t , u2U2cos2t。1211cos coscos()cos()22p qxyxyxypq (59) (510) 得得要实现乘法运算，应从三个方面考虑要实现乘法运算，应从三个方面考虑: （1）从非线性器件的特性考虑。）从非线性器件的特性考虑。 （2）从电路考虑。）从电路考虑。 （3）从输入信号

5、的大小考虑。）从输入信号的大小考虑。 利用式（利用式（57）和三角函数的积化和差公式）和三角函数的积化和差公式nmmmnmnnnuuCai0210 5.1.2 线性时变电路分析法线性时变电路分析法 对式对式 在在EQ+u2上对上对u1用泰勒级数展开用泰勒级数展开,有有12222121( )21()1()()()2!1()!QQQQnnQif Euuf EufEu ufEu ufEu un(511) ( )if u与式（与式（55）相对应）相对应,有有(55) (512)022Q )(nnnuauEf1122Q )(nnnunauEf ! 2 )(2222Q nnnnnnuaCuEfnmmmnm

6、nnnuuCai0210 若若u1足够小足够小,可以忽略式（可以忽略式（511）中）中u1的二次方及的二次方及其以上各次方项其以上各次方项,则上式化简为则上式化简为221()()QQif EufEu u(513) 01( )( )iI tg t u（514) 可表示为：可表示为：12222121( )21()1()()()2!1()!QQQQnnQif Euuf EufEu ufEu ufEu un 考虑考虑u1和和u2都是余弦信号，都是余弦信号，u1U1cos1t，u2U2cos2t，时变偏置电压时变偏置电压EQ（t）=EQ+U2cos2t，为一周期性函数，为一周期性函数,故故I0（t）、）

7、、g（t）也必为周期性函数）也必为周期性函数,可用傅里叶级数展开可用傅里叶级数展开,得得（515）(516) 01( )( )iI tg t utItIItUEftI2022010022Q02coscos)cos()(tgtggtUEftg2221022Q2coscos)cos()(221()()QQif EufEu u两个展开式的系数可直接由傅里叶系数公式求得两个展开式的系数可直接由傅里叶系数公式求得0022212222022222221(cos)21(cos)cos1,2,3,1(cos)21(cos)cos1,2,3,QkQQkQIf EUt dtIf EUtktdtkgfEUt dtg

8、fEUtktdtk(517) (518) 也可从式（也可从式（511）中获得）中获得2102222102112222201,0,1,2,2(2),0,1,2,2nn kkn kn kn knnn kkn kn kn knICaUknkgnkCaUk 频率分量为频率分量为2的各次谐波分量及其与的各次谐波分量及其与1的频率组合分量为：的频率组合分量为：(520) 01( )( )iI tg t u代入代入tItIItUEftI2022010022Q02coscos)cos()(tgtggtUEftg2221022Q2coscos)cos()(2q21q 频率分量为频率分量为2的各次谐波分量及其与的

9、各次谐波分量及其与1的频率组合分量为：的频率组合分量为：(520) tItIItUEftI2022010022Q02coscos)cos()(tgtggtUEftg2221022Q2coscos)cos()(2q21q 例例1 一个晶体二极管一个晶体二极管,用指数函数逼近它的伏安特性用指数函数逼近它的伏安特性,即即(1)TTuuVVesiI eI e在线性时变工作状态下在线性时变工作状态下,上式可表示为上式可表示为(521) （522） 式中式中(523) (524)QQ2222TTT2coscos0ssQ( )eeeeEuUEtxtVVVI tIIIgQ=IQ/VTQQ222TTT22Q2c

10、oscosssQTTd( )eeeedEuUEtxtVVVu EuIIig tguVV01( )( )iI tg t uuEQ+u1+u22222cos02221cos222()2()cos1()cos2xtnnxtnexxntxentdt(526)是第一类修正贝塞尔函数。因而是第一类修正贝塞尔函数。因而00222102221( )()2()cos( )()2()cosQnnQnnI tIxxntg tgxxnt(527) 01( )( )iI tg t up,q =|p1q2| p=0、1图图53 线性时变电路完成频谱的搬移线性时变电路完成频谱的搬移 线性时变器 件滤波器u1uou25.2

11、二极管电路二极管电路 5.2.1 单二极管电路单二极管电路 单二极管电路的原理电路如图单二极管电路的原理电路如图54所示所示,输入信号输入信号u1和和控制信号（参考信号）控制信号（参考信号）u2相加作用在非线性器件二极管上。相加作用在非线性器件二极管上。H(j)u1u2uoVDiD 图图54 单二极管电路单二极管电路 忽略输出电压忽略输出电压uo对回路的反作用对回路的反作用,这这样样,加在二极管两端的电压加在二极管两端的电压 uD为为12Duuu（528）二极管可等效为一个受控开关二极管可等效为一个受控开关,控制控制电压就是电压就是uD 。有。有0DDDpDDpg uuViuV(529) H(

12、j)u1u2uoVDiD 由前已知由前已知,U2U1,而而uDu1+u2,可进一步认为二极管的通可进一步认为二极管的通断主要由断主要由u2控制控制,可得可得220DDpDpg uuViuV(530) 一般情况下一般情况下, Vp 较小较小,有有U2 Vp ,可令可令Vp=0(也可在也可在电路中加一固定偏置电压电路中加一固定偏置电压E0 ,用以抵消用以抵消Vp,在这种情况下，在这种情况下，uDE0+u1+u2）,式（式（530）可进一步写为）可进一步写为22000DDDg uuiu (531) 图55 二极管伏安持性的折线近似uti0u(a)u0(b)iVpgDrD1u0(c)igDSucgD(

13、t)gD(1/rD)(d) 由于由于u2U2 cos2t ,则则u20对应于对应于 2n-/22t2n+/2 ,n=0,1,2,故有故有 222222302222DDDg untnintn(532) 上式也可以合并写成上式也可以合并写成2( )()DDDDig t ug Kt u(533) 式中式中, g（t）为时变电导）为时变电导,受受u2的控制的控制; K（2t）为开关函数）为开关函数,它在它在u2的正半周时等于的正半周时等于1,在负半周时为零在负半周时为零,即即22212222()302222ntnKtntn(534) 如图如图56所示所示,这是一个单向开关函数。由此可见这是一个单向开关

14、函数。由此可见,在前面的假设条件下在前面的假设条件下,二极管电路可等效一线性时变电二极管电路可等效一线性时变电路路,其时变电导其时变电导g（t）为）为2( )()Dg tg Kt（535） 图56 u2与K（2t）的波形图 2t02t012t)u2 K（2t）是一周期性函数）是一周期性函数,其周期与控制信号其周期与控制信号u2的周期相同的周期相同,可用一傅里叶级数展开可用一傅里叶级数展开,其展开式为其展开式为2222121222()coscos3cos52352( 1)cos(21)(21)nKttttntn (536) 代入式代入式2221222coscos3cos5235DDDigtttu

15、(537) 2( )()DDDDig t ug Kt u有有21uuuD其中其中(538) 2221222coscos3cos5235DDDigtttutUgtUgtUgtUgtUgtUgtUgtUgtUgtUgUgi)5cos(52 )5cos(52 )3cos(32 )3cos(32)cos(2 )cos(24cos52 2cos32 cos2cos2121D121D121D121D121D121D22D22D22D11D2DD121122coscosDuuuUtUt 由上式可以看出由上式可以看出,流过二极管的电流流过二极管的电流iD中的频率分量有中的频率分量有:（1）输入信号）输入信号u

16、1和控制信号和控制信号u2的频率分量的频率分量1和和2;（2）控制信号）控制信号u2的频率的频率2的偶次谐波分量的偶次谐波分量;（3）由输入信号）由输入信号u1的频率的频率1与控制信号与控制信号u2的奇次谐波分的奇次谐波分量的组合频率分量量的组合频率分量(2n+1)21 , n=0,1,2,。tUgtUgtUgtUgtUgtUgtUgtUgtUgtUgUgi)5cos(52 )5cos(52 )3cos(32 )3cos(32)cos(2 )cos(24cos52 2cos32 cos2cos2121D121D121D121D121D121D22D22D22D11D2DD 5.2.2 二极管平

17、衡电路二极管平衡电路 1电路电路 图图57（a）是二极管平衡电路的原理电路。它是由两个性）是二极管平衡电路的原理电路。它是由两个性能一致的二极管及中心抽头变压器能一致的二极管及中心抽头变压器T1、T2接成平衡电路的。接成平衡电路的。 图57 二极管平衡电路 2工作原理工作原理 与单二极管电路的条件相同与单二极管电路的条件相同,二极管处于大信号工作状态二极管处于大信号工作状态,即即U20.5V。这样。这样,二极管主要工作在截止区和线性区二极管主要工作在截止区和线性区,二极管二极管的伏安特性可用折线近似。的伏安特性可用折线近似。U2U1,二极管开关主要受二极管开关主要受u2控制。控制。若忽略输出电

18、压的反作用若忽略输出电压的反作用,则加到两个二极管的电压则加到两个二极管的电压uD1、uD2为为 uD1=u2+u1 uD2=u2-u1 （539） 由于加到两个二极管上的控制电压由于加到两个二极管上的控制电压u2是同相的是同相的,因此两个因此两个二极管的导通、截止时间是相同的二极管的导通、截止时间是相同的,其时变电导也是相同的。其时变电导也是相同的。由此可得流过两管的电流由此可得流过两管的电流i1、i2分别为分别为111221212221( )()()( )()()DDDDig t ug Kt uuig t ug Kt uu（540）i1、i2在在T2次级产生的电流分别为次级产生的电流分别为

19、: (541) 1121L1iiNNi2221L2iiNNi 但两电流流过但两电流流过T2的方向相反的方向相反,在在T2中产生中产生的磁通相消的磁通相消,故次级总电流故次级总电流 iL应为应为1212212()LLLLDiiiiiig Kt u(542)(543)将式（将式（540）代入上式）代入上式,有有考虑考虑u1U1cos1t , 代入上式可得代入上式可得1112112112112122coscos()cos()22cos(3)cos(3)33LDDDDDig Utg Utg Utg Utg Ut(544) 111221212221( )()()( )()()DDDDig t ug Kt

20、 uuig t ug Kt uu（540） 当考虑当考虑RL的反映电阻对二极管电流的影响时的反映电阻对二极管电流的影响时,要用要用包含反映电阻的总电导来代替包含反映电阻的总电导来代替gD。如果。如果T2次级所接负次级所接负载为宽带电阻载为宽带电阻,则初级两端的反映电阻为则初级两端的反映电阻为4RL。对。对i1、i2各支路的电阻为各支路的电阻为2RL。此时用总电导。此时用总电导12DLgrR(545) 图图58 二极管桥式电路二极管桥式电路 u1Bu2u1T1(a)RLT2R2L1L1u2R1uo(t)Ec EcRLCLuo(t)ieRe(b)A21()ABuKt u（546） 5.2.3二极管

21、环形电路二极管环形电路 1基本电路基本电路图图59（a）为二极管环形电路的基本电路。与二极管平衡电）为二极管环形电路的基本电路。与二极管平衡电路相比路相比,只是多接了两只二极管只是多接了两只二极管VD3和和VD4,四只二极管方向一四只二极管方向一致致,组成一个环路组成一个环路,因此称为二极管环形电路。因此称为二极管环形电路。图59 二极管环形电路 2工作原理工作原理 二极管环形电路的分析条件与单二极管电路和二极管平二极管环形电路的分析条件与单二极管电路和二极管平衡电路相同。平衡电路衡电路相同。平衡电路1与前面分析的电路完全相同。根据图与前面分析的电路完全相同。根据图59（a）中电流的方向）中电

22、流的方向,平衡电路平衡电路1和和2在负载在负载RL上产生的总电上产生的总电流为流为 iL=iL1+iL2=(i1-i2)+(i3-i4) （547）iL=iL1+iL2=(i1-i2)+(i3-i4) （547）2221212()2()2LDDTig Ktug Ktu （548）12D1Lu) t(Kg2i221212()()2()LDDigKtKtug Kt u221212()()2()LDDigKtKtug Kt u(549） 图图510 环形电路的开关函数波形图环形电路的开关函数波形图 2t02t012t)u2(t)2t012t )2t012t)1由此可见由此可见K（2t ）、）、K（2

23、t -）为单向开关函数）为单向开关函数,K（2t）为）为双向开关函数双向开关函数,且有且有2222210()()()10uKtKtKtu（550） （551）2t02t012t)u2(t)2t012t )2t012t)122()()1KtKt由此可得由此可得K（2t-）、）、K(2t）的傅里叶级数）的傅里叶级数:222222()1()1222coscos3cos52352( 1)cos(21)(21)nKtKttttntn (552) (553) 22222212()()()444coscos3cos5354( 1)cos(21)(21)nKtKtKttttntn 当当u1=U1cos1t时时

24、, 12112112112112112144cos()cos()44cos(3)cos(3)3344cos(5)cos(5)55LDDDDDDig Utg Utg Utg Utg Utg Ut(554) 在平衡电路的基础上，又消除了在平衡电路的基础上，又消除了u1的基波，且输出的幅度的基波，且输出的幅度增加了两倍。增加了两倍。221212()()2()LDDigKtKtug Kt u图图511 实际的环形电路实际的环形电路图512 双平衡混频器组件的外壳和电原理图13572468(a)T1VD4VD1VD2VD35678LO1F34RF12(b)T25.3 差分对电路差分对电路 5.3.1 单

25、差分对电路单差分对电路 1.电路电路 基本的差分对电路如图基本的差分对电路如图514所示。图中两个晶体管所示。图中两个晶体管和两和两 个电阻精密配对（这在集成电路上很容易实现）。个电阻精密配对（这在集成电路上很容易实现）。Ec Ecube2ube1uDAuoABie2ie1V1V2RLRLic1ic2I000120()()22eeIIiiIII (555) Ec Ecube2ube1uDAuoABie2ie1V1V2RLRLic1ic2I02. 传输特性传输特性 设设1 ,V2管的管的1，则有，则有ic1ie1 ，ic2ie2 ，可得晶体管的，可得晶体管的集电极电流与基极射极电压集电极电流与基

26、极射极电压 ube的关系为的关系为 112212bebeTbebeTuquVKTcssuquVKTcssiI eI eiI eI e(556) 112212bebeTbebeTuquVKTcssuquVKTcssiI eI eiI eI e(556) 由式由式(555)，有，有12121()012221(1)bebebebeTTTTuuuuVVVccsscuVcIiiI eI eieie(557) (558) (558) Ec Ecube2ube1uDAuoABie2ie1V1V2RLRLic1ic2I0Te1oc2VuIiTe1oc1VuIi(560) (561) (562) Hyperbo

27、lic tangentT0000c1T2tanh222221 euVIIIIuiV00c1Ttanh222IIuiV00c20c1Ttanh222IIuiIiVT0c21 euVIiT0c11euVIi 双端输出的情况下有双端输出的情况下有(563) 可得等效的差动输出电流可得等效的差动输出电流 io 与输入电压与输入电压u的关系式的关系式( 5 64) Ec Ecube2ube1uDAuoABie2ie1V1V2RLRLic1ic2I0Tooc12tanh22VuIIiTooc22tanh22VuIIioc2c1cc2Lcc1LLc1c2LoT()()()tanh2uuuEi REi RuR

28、 iiR IVoc1c2oTtanh2uiiiIV图图515 差分对的传输特性差分对的传输特性00c1Ttanh222IIuiV00c2Ttanh222IIuiVoc1c2oTtanh2uiiiIV（1）ic1、ic2和和 io与差模输入电压与差模输入电压u是非线性关系是非线性关系双曲正切双曲正切函数关系函数关系,与恒流源与恒流源I0成线性关系。双端输出时成线性关系。双端输出时,直流抵消直流抵消,交流交流输出加倍。输出加倍。 （2）输入电压很小时）输入电压很小时,传输特性近似为线性关系传输特性近似为线性关系,即工作即工作在线性放大区。这是因为当在线性放大区。这是因为当|x|100mV时时,电路

29、呈现限幅状态电路呈现限幅状态,两管接近于开关状态两管接近于开关状态,因此因此,该电路该电路可作为高速开关、限幅放大器等电可作为高速开关、限幅放大器等电路。路。（4）小信号运用时的跨导即为传输特性线性区的斜率）小信号运用时的跨导即为传输特性线性区的斜率,它表示电路在放大区输出时的放大能力它表示电路在放大区输出时的放大能力, 000202omuTiIgIuV(565) o0Ttanh2uiIV0iouu0ttio0 (5）当输入差模电压）当输入差模电压u=U1cos1t时时,由传输特性可得由传输特性可得 io波形波形,如图如图516。其所含频率分量可由。其所含频率分量可由tanh（u/2VT）的傅

30、里叶级数）的傅里叶级数展开式求得展开式求得,即即图图516 差分对作放大时差分对作放大时 io 的输出波形的输出波形Too2tanhVuIi(566) (567) 由差模电压由差模电压u=U1cos1t 令令x=U1/2VT的傅里叶级数展开式的傅里叶级数展开式Too2tanhVuIi1112o151311oo)12cos()( 5cos)(3cos)(cos)()(nntnxItxtxtxIti11112d)12cos(cos2tanh1)(ttntxxn 3. 差分对频谱搬移电路差分对频谱搬移电路 差分对电路的可控通道有两个差分对电路的可控通道有两个:一个为输入差模电压一个为输入差模电压,另

31、一个另一个为电流源为电流源I0;故可把输入信号和控制信号分别控制这两个通道。故可把输入信号和控制信号分别控制这两个通道。图图517 差分对频谱搬移电路差分对频谱搬移电路 H(j)H(j)EcuA EcuBV3V1V2uoReToo2tanhVuIi33Bbeeeeuui REH(j)H(j)EcuA EcuBV3V1V2uoRe0300000( )(1)( )( )tanh()(1)tanh()22( )(1)2eeBBeeeeeABAoTeTBAoeTEEuuI tiIIRRERuuui tI tIVEVuui tIEV忽略3beu 5.3.2 双差分对电路双差分对电路 双差分对频谱搬移电路

32、如图双差分对频谱搬移电路如图518所示。它由三个基本所示。它由三个基本的差分电路组成的差分电路组成,也可看成由两个单差分对电路组成。也可看成由两个单差分对电路组成。V1、V2、V5组成差分对电路组成差分对电路,V3、V4、V6组成差分对电路组成差分对电路,两两个差分对电路的输出端交叉耦合。个差分对电路的输出端交叉耦合。EcV2V1V4V3V6V5RLuouAuBI0i1i2i3i4i6i5i1RLi2io= iI iII = (i1+ i3) - (i2+ i4) = (i1 - i2) - (i4- i3) （572）ToLc2c1LLc1cLc2cc1c2o2tanh)()()(VuIRi

33、iRRiERiEuuu125436565600tanh()2tanh()2()tanh()2tanh()2tanh()tanh()22ATATAoTBTABoTTuiiiVuiiiVuiiiVuiiIVuuiIVV(573) (574) (575) （576） EcV2V1V4V3V6V5RLuouAuBI0i1i2i3i4i6i5i1RLi2io= iI iII = (i1+ i3) - (i2+ i4)= (i1 - i2) - (i4- i3) 当当u1=U1cos1t，u2=U2cos2t 时时,代入式（代入式（576）有）有2112121200()()cos(21)cos(21)oo

34、mnmniIxxmtnt (577) 120122224ooTTTuuIiIu uVVV(578) TBTA0o2tanh2tanhVuVuIi图图519 接入负反馈时的差分对电路接入负反馈时的差分对电路V5Re2V6ie5ie6I0uB55265256552111222Bbeeebeeebebeeeeuui Rui RuuiiR式中，式中，ube5 - ube6=VTln（ie5/ie6），因此上式可表示为），因此上式可表示为 55626556265625621ln()21()ln211()()22eBTeeeeeeeeTeBeeeeiuViiRiiiiRViuiiRii R(580) (5

35、81) (582) 112212bebeTbebeTuquVKTcssuquVKTcssiI eI eiI eI e参考参考V5Re2V6ie5ie6I0uB 考虑到考虑到ie5ie6=I0,则由式（则由式（582）可知）可知,为了保证为了保证ie5和和ie6大于零大于零,uB的最大动态范围为的最大动态范围为00222222tanh()22()BeBAoeToABeIuIRuuiRViKt uR(583) (584)(585) )V2utanh()ii (iR)ii (21uTA65o2e65B由由和和得得V9500500V7VEE(8 V)6.8 k514500V8MC159632RyV6V

36、514uy810uxV1V2V3V4RcRc3.9 k3.9 kVCC( 12 V)126uoic3ic4ic6ic5ic2ic1iaib图图520 MC1596的内部电路的内部电路5.4 其它频谱线性搬移电路其它频谱线性搬移电路 5.4.1 晶体三极管频谱线性搬移电路 EbEcu2u1f0ic图521 晶体三极管频谱搬移原理电路 5.4.1 晶体三极管频谱线性搬移电路晶体三极管频谱线性搬移电路 可将可将ic表示为表示为1212113( )11()()( )1( )( )( )211( )( )3!cbebbcbbbnnbbif uf uuEf E tuif E tf E t ufE t uf

37、E t ufE t un在时变工作点处在时变工作点处,将上式对将上式对u1展开成泰勒级数展开成泰勒级数,有有（586） (587) EbEcu2u1f0ic 图522（a）给出了icube曲线,同时画出了Ic0（t）波形,其表示式000012022( )( )01222( )coscos2()( )( )coscos2bebbebcccccbebuEtuEtbebemmmmItIItItdidf uf E tdudugtggtgt(588) (589) （590） 式中式中,gm0是是gm（t）的平均分量（直流分量）的平均分量（直流分量）,它不一定是直流它不一定是直流工作点工作点 Eb处的跨导。处的跨导。gm1是是gm（t）中角频率为）中角频率为2分量的振幅分量的振幅时