上教版高二数学教案—矩阵的概念

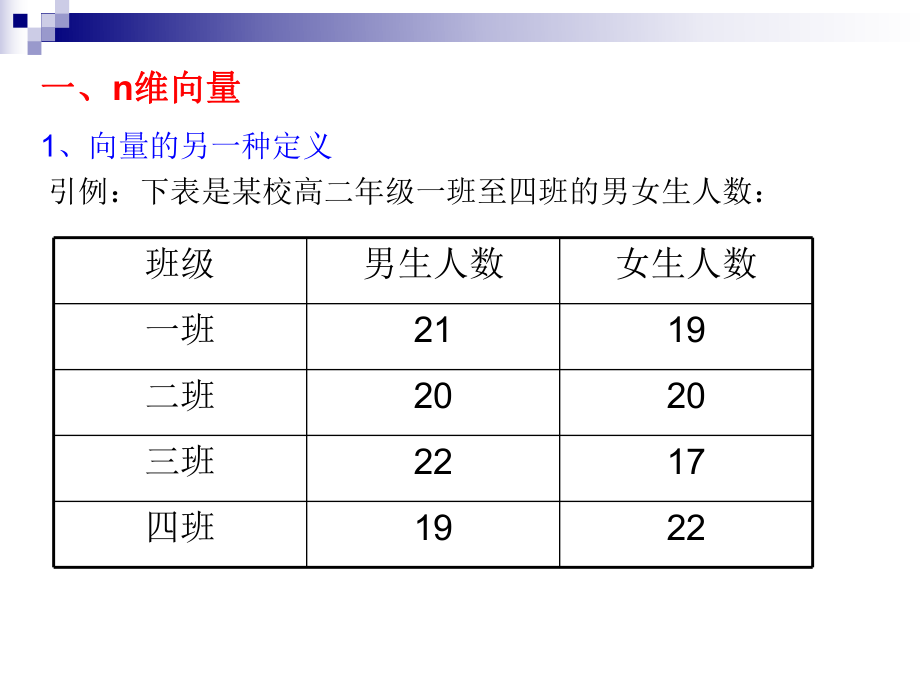
1、矩阵和行列式初步9.1矩阵的概念教学目标：教学目标：1了解矩阵、方阵、二维向量、三维向量、 n维向量、行向量、列向量的概念； 2掌握n维向量的加减法、实数与向量乘积、 向量的数量积的运算法则； 3理解同阶的矩阵，理解相等的矩阵； 4理解线性方程组及其增广矩阵的转换； 5掌握运用基本变换求线性方程组的解。教学重点：教学重点：矩阵等相关概念教学难点：教学难点：用矩阵的基本变换求线性方程组。一、一、n维向量维向量1、向量的另一种定义引例：下表是某校高二年级一班至四班的男女生人数：班级男生人数女生人数一班2119二班2020三班2217四班19222、定义、定义123123,( ,)(1,2, )nn

2、inx x xxx x xxx inni维由 个有序实数组成的数组叫做，其中叫该向向量的第量分量。注：注：与2维向量研究方向和模的大小不同，在n维向量问题上我们只关心它们在各个位置上所对应的数，而并不关心向量的方向和模所表示的意义。3、n维向量的运算维向量的运算类比平面向量的运算即可得123123( ,),(,),(1,2, ),nniiax x xxby yyyx yR in设为任意实数，规定：112233(,)nnabxy xyxyxy123(,)naxxxx112233nna bx yx yx yx y 容易验证，对n维向量，类似2维向量的运算律仍然成立。如：;();()abbamn a

3、manaabca cb c 等例1：统计某校高二（1）班的5名学生的数学平时、期中、期末成绩如下表：学号平时成绩期中成绩期末成绩18292882787677396909349296915849285（1）写出这5名学生数学平时、期中、期末的成绩向量；（2）写出这5名学生数学平时、期中、期末的总成绩向量；（3）写出这5名学生数学平时、期中、期末的平均成绩向量；（4）若以平时成绩的30，期中考试成绩的30，期末考试成绩的40作为该学期的总成绩，试写出相应的权重向量，并求5号学生该学期的总成绩。二、矩阵二、矩阵111212122212(1,2,;1,2, )ijnnmmmnm na im jnaaa

4、aaamnaaa由个实数排成的 行、 列的长方阵形式：(1,2,;1,2, )()ijm na im jjAnim nA叫做，其中叫做矩阵第 行第 列的。矩阵通常用一个大写字母表示。如上阶的矩阵元素述矩表示为或阵可mnn如果矩阵的行数 和列数 相等，我们把它称作 阶方阵；ABAB如果矩阵 和 的行数和列数分别相等，那么 与 叫做同阶矩阵。行向量，列向量，相等矩阵概念学号平时成绩期中成绩期末成绩18292882787677396909349296915849285可将表格中的成绩用一个5行3列的矩阵表示，即：829288787677969093929691849285也可表示成如下的矩阵：827

5、896928492769096928877939185例2：某公司销售部门一季度四名销售员的销售业绩如下表：姓名一月份二月份三月份小李453770小王504866小张776088小陈282950（1）将四名销售员的业绩用矩阵表示；（2）写出行向量、列向量并指出实际意义。253,2020, , .xxxyABABxx y A例 ：已知矩阵且求25438xyxy例 ：用加减消元法解下列方程组：1231125318矩阵叫做方程组的；矩阵叫做方程组的系数矩阵增广矩阵。1001叫做单位矩阵。注：解方程组的过程即是将方程组的系数矩阵通过矩阵变注：解方程组的过程即是将方程组的系数矩阵通过矩阵变换变为单位矩阵的过程。换变为单位矩阵的过程。例5：九章算术第八卷方程中的一题：5头牛2只羊值10两金，2头牛5只羊