第1章逻辑代数

1、第一章第一章 逻辑代数基础逻辑代数基础1.1 概述概述1.2 数制与码制数制与码制1.3 基本逻辑运算基本逻辑运算1.4 逻辑代数基本定理及常用公式逻辑代数基本定理及常用公式1.5 逻辑函数及其表示方法逻辑函数及其表示方法1.6 逻辑函数的化简逻辑函数的化简基本要求(掌握)：1.掌握数值的二进制表示法、二进制数与十进制数之间的转换方法。2.掌握三种基本和四种常用逻辑运算。3.掌握三个特殊定理，四个常用公式。4.掌握逻辑函数的公式化简法和图形化简法。5.几种常用的表示逻辑函数的方法。基本要求（理解）：1.理解二进制代码的概念。2.与、或、非三个重要概念的物理意义。3.逻辑变量与逻辑函数。4.最小

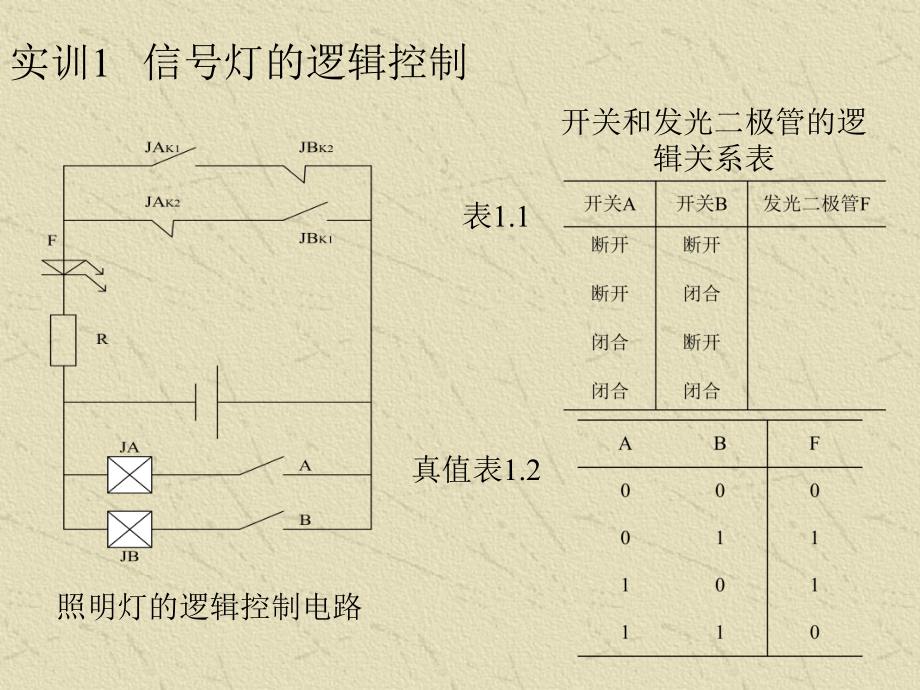
2、项的概念和性质。5.标准与或表达式、最简与或表达式和最简与非-与非表达式的特点。6.约束和约束项的概念、约束项的表示方法及其在逻辑函数化简中的应用。7.逻辑函数几种常用表示方法各自的主要特点。重点：逻辑函数的化简方法，尤其是图形化简法。难点：约束的概念，约束项的定义、性质、表示方法及其在逻辑函数化简中的应用。也是重点。照明灯的逻辑控制电路开关和发光二极管的逻辑关系表表1.1真值表1.2实训1 信号灯的逻辑控制1.1 概述概述1. 数字量与模拟量的概念数字量与模拟量的概念数字量：数字量：定义：仅能取某一区间内若干个特定值的物理量。定义：仅能取某一区间内若干个特定值的物理量。特点：数字量的变化在时

3、间上和数值上都是离散的。特点：数字量的变化在时间上和数值上都是离散的。模拟量模拟量定义：可在某一连续区间内任意取值的物理量。定义：可在某一连续区间内任意取值的物理量。特点：模拟量的变化在时间上和数值上都是连续的。特点：模拟量的变化在时间上和数值上都是连续的。1.1 概述概述1. 数字量与模拟量的概念数字量与模拟量的概念模拟信号：在时间上和数值上连续的信号。数字信号：在时间上和数值上不连续的（即离散的）信号。uu模拟信号波形数字信号波形tt对模拟信号进行传输、处理的电子线路称为模拟电路。对数字信号进行传输、处理的电子线路称为数字电路。数字信号波形数字信号波形-脉冲信号脉冲信号数字信号波形即脉冲信

4、号，是指作用时间很短数字信号波形即脉冲信号，是指作用时间很短的突变电压信号或电流信号的统称，从广义上的突变电压信号或电流信号的统称，从广义上说，凡不具有连续正弦波的信号，均可称为脉说，凡不具有连续正弦波的信号，均可称为脉冲信号。冲信号。主要参数主要参数六个特征参数定义如下：六个特征参数定义如下：脉冲周期脉冲周期 ：周期性脉冲序列中，两个相邻脉：周期性脉冲序列中，两个相邻脉冲出现的时间间隔。冲出现的时间间隔。脉冲幅值脉冲幅值 ：脉冲信号的最大变化幅值。：脉冲信号的最大变化幅值。占空比占空比 ：脉冲信号的正脉冲宽度与脉冲周期的：脉冲信号的正脉冲宽度与脉冲周期的比值，即比值，即 TmUDW/DtT脉

5、冲宽度脉冲宽度 ：从脉冲波形上升沿的：从脉冲波形上升沿的 到下降沿的到下降沿的 所需的时间。所需的时间。上升时间上升时间tr：脉冲波形由：脉冲波形由0.1Um上升到上升到0.9Um所需的时间。所需的时间。下降时间下降时间tf：脉冲波形由：脉冲波形由0.9Um下降到下降到0.1Um所需的时间。所需的时间。Wtm0.5Um0.5U2. 数字电路的分类数字电路的分类（1 1）据电路结构和工作原理据电路结构和工作原理 组合逻辑电路：无记忆功能，其输出仅取决于组合逻辑电路：无记忆功能，其输出仅取决于当时输入。当时输入。 时序逻辑电路：有记忆功能，其输出由当时时序逻辑电路：有记忆功能，其输出由当时输入和电

6、路状态共同决定。输入和电路状态共同决定。（2 2）按集成度按集成度 SSI、MSI、LSI。（3 3）按制作工艺按制作工艺 TTL、CMOS。1.1 概述概述3. 数学工具和描述方法数学工具和描述方法（1 1）数学工具数学工具 逻辑代数逻辑代数（2 2）描述方法描述方法 真值表真值表 逻辑表达式逻辑表达式 波形图波形图 逻辑电路图逻辑电路图 硬件描述语言硬件描述语言1.2 数制和码制数制和码制数制进位制基数位权数制进位制基数位权（1 1）进位制进位制：逢基进一。用多位数码表示数时，：逢基进一。用多位数码表示数时，从低位到高位的进位规则。从低位到高位的进位规则。 如：如：9+1=10（2 2）基

7、基 数数：数码的个数。进位制中单位代码：数码的个数。进位制中单位代码所能表达的最大数加所能表达的最大数加1 1，即逢几进一。，即逢几进一。（3 3）位位 权权：数码所在位置表示数值的大小。数：数码所在位置表示数值的大小。数的每一位的大小都对应着该位上的数码乘上一个的每一位的大小都对应着该位上的数码乘上一个固定的数，这个固定的数就是这一位的位权。固定的数，这个固定的数就是这一位的位权。=3 102 + 3 101+ 3 100+ 3 10-1 +3 10-2333.331.2.1 几种常用的计数制几种常用的计数制1. 十进制十进制=3 102 + 3 101+ 3 100+ 3 10-1 +3

8、10-2权权 权权 权权 权权 权权特点：特点：a.a.基数基数1010，逢十进一；，逢十进一； b. 0-9b. 0-9十个数码；十个数码； c.c.第第i i位的位权为位的位权为1010i i。 (333.33)10(D)10=(kn-1 k1 k0. k-1 k-m)10=kn-110n-1+k1101+k0100 + k-110-1+k-m10-m110nmiiik2. 二进制二进制特点：特点：a. a. 基数基数2 2，逢二进一，即，逢二进一，即1+1=101+1=10 b. b. 有有0-10-1两个数码两个数码 c.c.第第i i位的位权为位的位权为2 2i i。(D)(D)2

9、2=(k=(kn-1 n-1 k k1 1 k k0. 0. k k-1 -1 k k-m-m) )2 2 =k =kn-1 n-1 2 2n-1n-1+ +k+k1 1 2 21 1+k+k0 0 2 20 0 + k k-1 -1 2 2-1-1+ +k k-m -m 2 2-m-minmiik 21a. a. 基数基数R R，逢，逢R R进一进一b. b. 有有R R个数码个数码c. c. 第第i i位的位权为位的位权为R Ri i。(D)(D)R R=(k=(kn-1 n-1 k k1 1 k k0. 0. k k-1 -1 k k-m-m) )2 2 =k =kn-1 n-1 R R

10、n-1n-1+ +k+k1 1 R R1 1+k+k0 0 R R0 0 +k+k-1 -1 R R-1-1+ +k k-m -m R R-m-m1nmiiiRk3. 任意进制任意进制1.2.2. 数制间的相互转换数制间的相互转换十进制与非十进制间的转换十进制与非十进制间的转换非十进制间的转换非十进制间的转换十进制十进制非十进制非十进制非十进制非十进制十进制十进制二进制二进制八、十六进制八、十六进制八、十六进制八、十六进制二进制二进制1. 非十进制转成十进制非十进制转成十进制方法：方法：将相应进制的数按权展成多项式，将相应进制的数按权展成多项式，按十进制求和按十进制求和(F8C.B)(F8C.

11、B)16 16 = = F F16162 2+8+816161 1+C+C16160 0+B+B1616-1-1= = 3840+128+12+0.68753840+128+12+0.6875=3980.6875=3980.6875例例1.2.11.2.1：例例1.2.21.2.2：二、八、十六进制转换为十进制：二、八、十六进制转换为十进制(111.11)8 182 181 180181 182 (73.140625)10(111.11)16116211611160116-1116-2 (273.06640625)10(111.11)2 122121 1201 21 122 (7.75)10小

12、数部分转换：小数部分转换： 乘基取整法：小数连续乘以目标数制的基数乘基取整法：小数连续乘以目标数制的基数（R R），先得到的整数为高位，后得到的为低位。），先得到的整数为高位，后得到的为低位。 终止：小数部分为终止：小数部分为“0”0”，或满足要求精度。，或满足要求精度。整数部分转换：整数部分转换： 除基取余法：用目标数制的基数（除基取余法：用目标数制的基数（R R）连续去）连续去除十进制数，直至余数为除十进制数，直至余数为0 0。先得到的余数为低位，。先得到的余数为低位，后得到的余数为高位。后得到的余数为高位。2. 十进制转换成非十进制十进制转换成非十进制 2 44 余数 低位 2 22 0

13、=K0 2 11 0=K1 2 5 1=K2 2 2 1=K3 2 1 0=K4 0 1=K5 高位 0.375 2 整数 高位 0.750 0=K1 0.750 2 1.500 1=K2 0.500 2 1.000 1=K3 低位整数部分：除基取余整数部分：除基取余小数部分：乘基取整小数部分：乘基取整(44.375)(44.375)1010(101100.011)(101100.011)2 23. 二进制转换成八、十六进制二进制转换成八、十六进制（1 1） 二进制转换为八进制二进制转换为八进制 以小数点为起点，将整数和小数部分每三位以小数点为起点，将整数和小数部分每三位分为一组，不足三位的加

14、分为一组，不足三位的加“0”0”补足，然后每组补足，然后每组用等值的八进制码替代。用等值的八进制码替代。例例1.2.31.2.3： 11010111.0100111 B = ? O11010111.0100111 B = ? O 11010111.0100111 B = 327.234 O11010111.0100111 B = 327.234 O11010111.0100111小数点为界小数点为界000723234（2 2） 二进制转换为十六进制二进制转换为十六进制 每四位分为一组。每四位分为一组。例例1.2.41.2.4： 111011.10101 B = ?111011.10101 B

15、= ? H H 111011.10101 B = 3B.A8 H 111011.10101 B = 3B.A8 H111011.1010100000B3A84. 十六、八进制转换成二进制十六、八进制转换成二进制方法：将十六、八进制数的每一位用等方法：将十六、八进制数的每一位用等值的值的4 4、3 3位二进制数代替即可。位二进制数代替即可。例例1.2.51.2.5 将下列十进制数转换成非十进制数：将下列十进制数转换成非十进制数： (89.875)(89.875)10 10 =( )=( )2 2 =( ) =( )8 8 =( ) =( )16161011001.1111011001.11113

16、1.7131.759.E59.E1.3 基本逻辑运算基本逻辑运算 布尔代数布尔代数描述客观事物逻辑关系的数描述客观事物逻辑关系的数学方法。广泛应用于解决开关电路和数字逻辑学方法。广泛应用于解决开关电路和数字逻辑电路的分析与设计上。电路的分析与设计上。 别名：开关代数、逻辑代数。别名：开关代数、逻辑代数。 逻辑代数逻辑代数布尔代数在二值逻辑电路布尔代数在二值逻辑电路中的应用。中的应用。1.3 基本逻辑运算基本逻辑运算1.3.1 基本逻辑运算基本逻辑运算与逻辑与逻辑或逻辑或逻辑非逻辑非逻辑只有决定某一事件的所有条件全部只有决定某一事件的所有条件全部具备，这一事件才能发生具备，这一事件才能发生逻辑表

17、达式逻辑表达式L= A L= A B = ABB = AB与逻辑真值表与逻辑真值表与逻辑关系表与逻辑关系表1. 与逻辑与逻辑开关开关A A 开关开关B B灯灯L L断断 断断断断 合合合合 断断合合 合合灭灭灭灭灭灭亮亮A AB BL L1 01 01 11 10 10 10 00 00 00 01 10 0A AB BL L 图形符号图形符号与逻辑运算符，也有用与逻辑运算符，也有用“ ”、“”、“”、“&”&”表示表示逻辑表达式逻辑表达式L= A L= A + + B B或逻辑真值表或逻辑真值表2. 或逻辑或逻辑 1 1图形符号图形符号只有决定某一事件的原因有一个或只有决定某

18、一事件的原因有一个或一个以上具备，这一事件才能发生一个以上具备，这一事件才能发生A AB BL L1 01 01 1 1 1 0 10 10 00 01 11 11 10 0A AB BL L3. 非逻辑非逻辑非逻辑真值表非逻辑真值表A AL L0 01 11 10 0逻辑表达式逻辑表达式F= A F= A 当决定某一事件的条件满足时，事当决定某一事件的条件满足时，事件不发生；反之事件发生件不发生；反之事件发生图形符号图形符号A AL L1 1L与非逻辑运算与非逻辑运算L=ABL=AB或非逻辑运算或非逻辑运算L=A+BL=A+B与或非逻辑运算与或非逻辑运算L=AB+CDL=AB+CD1.3.2

19、 常用复合逻辑运算常用复合逻辑运算LL异或运算异或运算A AB BL L1 1 0 01 11 10 0 1 10 0 0 01 11 10 00 0A AB BL L=1=1图形符号图形符号A AB BL L1 1 0 01 11 10 0 1 10 0 0 00 00 01 11 1同或运算同或运算逻辑表达式逻辑表达式L=A L=A B= B= A A B B 逻辑表达式逻辑表达式L=AL=A B=AB+ABB=AB+AB= =A AB BL L图形符号图形符号常用复合逻辑运算常用复合逻辑运算1.4 逻辑代数的基本定理及逻辑代数的基本定理及 常用公式常用公式1.4.1 逻辑代数的基本定律逻

20、辑代数的基本定律 A 1=A A+ 0=A0-10-1律律 A 0=0 A+ 1=1自等律自等律重叠律重叠律A A=A A+ A=AA A=0 A+A=1互补律互补律1. 常量变量关系常量变量关系2. 五个定律五个定律分配律分配律反演律反演律交换律交换律结合律结合律还原律还原律A B = B A A + B = B + A (A B ) C = A (B C) (A+ B )+ C = A+ (B+ C) A ( B + C ) = A B+ A C A + B C =( A + B) (A+ C )A B= A+B A+ B=AB A= A证明方法证明方法例例1.4.1 1.4.1 用真值表

21、证明反演律用真值表证明反演律A BA BAB A+ BA BA+B000110111110111010001000 A B= A+B A+ B=AB利用真值表利用真值表1.4.2 逻辑代数中的基本规则逻辑代数中的基本规则1. 代入规则代入规则 任何一个含有某变量的等式，如果等式中所有出现此变量的任何一个含有某变量的等式，如果等式中所有出现此变量的位置均代之以一个逻辑函数式，则此等式依然成立。位置均代之以一个逻辑函数式，则此等式依然成立。BCBACAB)()(DABCBDBABCDABCDAB)()(BCBDBABCDAB)(例：中，A的位置都用 代入。则：等式左边为：等式右边为：2. 反演规则

22、反演规则对逻辑函数式对逻辑函数式Y Y，做如下处理：，做如下处理： “.”“.”换成换成“+”, “+” +”, “+” 换成换成“.”;.”; “0”“0”换成换成“1”1”，“1”1”换成换成“0”0”； 原变量换成反变量，反变量换成原变量。原变量换成反变量，反变量换成原变量。 得到的新函数式称为原函数式得到的新函数式称为原函数式Y Y的反函数式的反函数式 。Y注：注：遵守原运算优先次序；遵守原运算优先次序；不属于单个变量上的反号应保留不变。不属于单个变量上的反号应保留不变。例例1.4.2 1.4.2 已知已知Y=A(B+C)+CDY=A(B+C)+CD, ,求求 。解：解：根据反演定理可

23、写出：根据反演定理可写出：Y)DC( )CBA(YDCBDACBCADACBCA例例1.4.31.4.3 已知已知Y=Y= , ,求求 。解：解：根据反演定理可写出：根据反演定理可写出：DEBCAYEDCBAY3. 对偶规则对偶规则对逻辑函数式对逻辑函数式Y Y，做如下处理：，做如下处理： “.”“.”换成换成“+”, “+” +”, “+” 换成换成“.”;.”; “0”“0”换成换成“1”1”，“1”1”换成换成“0”0”。 得到的新函数式称为原函数式得到的新函数式称为原函数式Y Y的对偶式的对偶式 。Y 原等式与其对偶式互为对偶式。原等式与其对偶式互为对偶式。 两函数式相等，则其对偶式也

24、相等两函数式相等，则其对偶式也相等例例1.4.41.4.4：B1CAABF )B 0() CA ()BA(F其对偶式其对偶式1.4.3 逻辑代数中的几个常用公式逻辑代数中的几个常用公式公式公式1ABAAB公式公式2AABABABAA公式公式3CAABBCCAAB公式公式4CAABBCDCAAB推论推论还原律还原律吸收律吸收律吸收律吸收律冗余律冗余律1.5 逻辑函数及其表示方法逻辑函数及其表示方法 若输入逻辑变量若输入逻辑变量A、B、C的取值确定，的取值确定，输出逻辑变量输出逻辑变量Y的值也唯一确定，则称的值也唯一确定，则称Y是是A、B、C的逻辑函数，写作：的逻辑函数，写作： Y=F（A，B，C

25、） 1.5.1逻辑函数的定义逻辑函数的定义（1）逻辑真值表）逻辑真值表（2）逻辑函数式）逻辑函数式（3）逻辑图）逻辑图（4）卡诺图）卡诺图（5）波形图）波形图1.5.2 逻辑函数的常用的表示方法逻辑函数的常用的表示方法1.1.逻辑真值表逻辑真值表 例例1.5.11.5.1： 举重裁判电路举重裁判电路三人三人表决电路，结果按表决电路，结果按“少数服从多数少数服从多数”的的原则决定，主裁判必须同意，试建立该原则决定，主裁判必须同意，试建立该逻辑函数。逻辑函数。1.5.2 逻辑函数的常用的表示方法逻辑函数的常用的表示方法1. 逻辑真值表逻辑真值表输输 入入输输出出Y YA B C0 0 000 0

26、100 1 000 1 101 0 001 0 111 1 011 1 113. 逻辑图逻辑图)(CBAY2. 逻辑函数式逻辑函数式1. 逻辑真值表逻辑真值表输输 入入输输出出Y YA B C0 0 000 0 100 1 000 1 101 0 001 0 111 1 011 1 113. 逻辑图逻辑图2. 逻辑函数式逻辑函数式4. 波形图波形图5.卡诺图卡诺图6.硬件描述语言硬件描述语言1.6 逻辑函数的化简逻辑函数的化简 意义：表达式最简意义：表达式最简电路最简电路最简节省器件，节省器件，降低成本，提高可靠性。降低成本，提高可靠性。 最简形式：函数式中乘积项个数不能再减少，且最简形式：函

27、数式中乘积项个数不能再减少，且每项中相乘的因子不能再减少。每项中相乘的因子不能再减少。 1.6.1 化简的意义化简的意义用公式法简化逻辑函数时，一方面，不仅要用公式法简化逻辑函数时，一方面，不仅要熟记逻辑熟记逻辑代数的基本公式，代数的基本公式，而且还需要有而且还需要有熟练的运算技巧熟练的运算技巧；另；另一方面，经过化简后的逻辑函数一方面，经过化简后的逻辑函数是否是最简是否是最简或最佳时或最佳时有时也难以确定。与之相比，应用卡诺图化简逻辑函有时也难以确定。与之相比，应用卡诺图化简逻辑函数，则简捷直观、灵活方便、且容易确定是否已得到数，则简捷直观、灵活方便、且容易确定是否已得到最简结果。但是，当逻

28、辑函数的变量数最简结果。但是，当逻辑函数的变量数n6以后，由以后，由卡诺图中小方格的相邻性已很难确定，使用就不很方卡诺图中小方格的相邻性已很难确定，使用就不很方便了。便了。标准或与表达式标准或与表达式标准或与表达式标准或与表达式是一种特殊的或与表达式，其中的每是一种特殊的或与表达式，其中的每个或项都包含了所有的逻辑变量，每个变量以原变量个或项都包含了所有的逻辑变量，每个变量以原变量或反变量出现一次且仅出现一次。这样的或项称为标或反变量出现一次且仅出现一次。这样的或项称为标准或项，又称准或项，又称最大项最大项。例如：例如：A、B、C的最大项的最大项 对应的变量取值组对应的变量取值组合为合为010

29、，其大小为，其大小为2，因而，记为，因而，记为M2。如果一个或项缺少某变量，则或上该变量和其反变量如果一个或项缺少某变量，则或上该变量和其反变量的逻辑与，直至每一个或项都为最大项为止。的逻辑与，直至每一个或项都为最大项为止。 ()ABC标准与或表达式标准与或表达式 最小项最小项定义：定义： 标准与或表达式标准与或表达式是一种特殊的与或表达式，其中的是一种特殊的与或表达式，其中的每个与项都包含了所有相关的逻辑变量，每个变量每个与项都包含了所有相关的逻辑变量，每个变量以原变量或反变量出现一次且仅出现一次，这样的以原变量或反变量出现一次且仅出现一次，这样的与项称为标准与项，又称与项称为标准与项，又称

30、最小项最小项。 如如 F=F(A, B) F=F(A, B)，共有最小项，共有最小项4 4项：项：,AB AB AB AB 逻辑函数常见形式：逻辑函数常见形式： 1.6.1 化简的意义化简的意义或非表达式或非非表达式或与与非表达式与非或表达式与- CA - - - BABACACAABCAABL 最常见：最常见： 与与-或表达式或表达式 1.6.2 代数化简法代数化简法1. 并项法并项法 运用公式运用公式 将两项合并为一项，消将两项合并为一项，消去一个变量。去一个变量。1 AA例例1.6.1 1.6.1 试用并项法化简下列逻辑函数：试用并项法化简下列逻辑函数：CAABCBABAF)B ()(2

31、解：解：CAABCBABAF)B ()(2CBAABCBCACBA )()(BBCABBACCCAAC1.6.2 代数化简法代数化简法2. 吸收法吸收法 运用公式运用公式 、 消去多余的与项。消去多余的与项。CAABBCCAABAABA例例1.6.2 1.6.2 试用吸收法化简下列逻辑函数：试用吸收法化简下列逻辑函数：解：解：ADDCADEACBAF2ADDCADEACBAF2ADADEDCACBA)(ADDCACBADCACBA1.6.2 代数化简法代数化简法3. 消项法消项法用用 消去多余的因子。消去多余的因子。 BABAABCCABAF1BCCBA)(BCBCABCA例例1.6.3 1.

32、6.3 试用消项法化简下列逻辑函数：试用消项法化简下列逻辑函数： （1 1） （2 2）BCCABAF1BBCAABF2BBCAABF2BCAAB)(BCA解解：（1 1）（2 2）1.6.2 代数化简法代数化简法4. 配项法配项法例例1.6.4 1.6.4 试用配项法化简下列逻辑函数：试用配项法化简下列逻辑函数： 运用公式运用公式 、 消去多余的消去多余的与项。与项。)(BBAAAAABACBCBBAF1BACBCBBAF1)()(CCBAAACBCBBACBABCAACBCBACBBA)()1 ()1 (BBCAACBCBACACBBA解：解：综合应用综合应用例例1.6.5 1.6.5 试

33、用配项法化简逻辑函数：试用配项法化简逻辑函数：解：解：EFBEFBABDCAABDAADFEFBEFBABDCAABDAADFEFBEFBABDCAABAEFBBDCAAEFBBDCA综合应用综合应用例例1.6.6 1.6.6 试用配项法化简逻辑函数：试用配项法化简逻辑函数：解：解：)(GFADEDBDBCBCBCAABF)(GFADEDBDBCBCBCAABF)()(GFADEDBDBCBCBCBA)()(GFADEDBDBCBCBCBADBDBCBCBGFADEA)()()(CCDBDBCBDDCBA )()()(CDBCBCDBDCBDBCDBA)()(CDBCBDCDBCDBACBDC

34、DBA1.1.最小项最小项 1.6.3 逻辑函数的卡诺图化简法逻辑函数的卡诺图化简法（1 1）概念）概念 最小项是逻辑函数自变量的乘积项，特点最小项是逻辑函数自变量的乘积项，特点: : 每一项都含有与函数的自变量个数相同数量每一项都含有与函数的自变量个数相同数量的变量因子；的变量因子； 每个自变量都以原变量或反变量的形式作为每个自变量都以原变量或反变量的形式作为一个因子在乘积项中出现且仅出现一次。一个因子在乘积项中出现且仅出现一次。1.1.最小项最小项 （2 2）性质）性质 对任意一个最小项，只有一组变量的取值使对任意一个最小项，只有一组变量的取值使其值为其值为1 1； 对变量的任一组取值，任

35、意两个不同的最小对变量的任一组取值，任意两个不同的最小项的乘积为项的乘积为0 0； 对变量的任一组取值，全体最小项之和为对变量的任一组取值，全体最小项之和为1。1.6.3 逻辑函数的卡诺图化简法逻辑函数的卡诺图化简法三变量最小项的编号表三变量最小项的编号表最小项最小项使最小项为使最小项为1 1的变量的变量取值取值对应的十进制对应的十进制数数编号编号A B C0 0 00 0 10 1 00 1 11 0 01 0 11 1 01 1 101234567m0m1m2m3m4m5m6m7BACAAAAAAABBBBBBBCCCCCCC2. 2. 逻辑函数的最小项表达式逻辑函数的最小项表达式 定义：

36、将所有使函数值为定义：将所有使函数值为1 1的最小项或在一起的最小项或在一起构成的与或式。构成的与或式。 任何逻辑函数式转化成唯一的最小项表达式。任何逻辑函数式转化成唯一的最小项表达式。举重裁判电路举重裁判电路三人表决电路三人表决电路ABCCABCBACBAL),()7 , 6 , 5(),(765mmmmCBAL1.6.3 逻辑函数的卡诺图化简法逻辑函数的卡诺图化简法3.3.卡诺图卡诺图 将将n n变量的最小项各用一个小变量的最小项各用一个小方块表示，并使逻辑相邻的最小项方块表示，并使逻辑相邻的最小项几何位置也相邻，所得到的图形。几何位置也相邻，所得到的图形。 ABABBAAB AB1010

37、ABC01000111100001111000011110 m0 m1 m2 m3 m4 m5 m6 m7 m0 m1 m2 m3 m4 m5 m6 m7 m12 m13 m14 m15 m8 m9 m10 m11ABCD二变量卡诺图二变量卡诺图三变量卡诺图三变量卡诺图四变量卡诺图四变量卡诺图1.6.3 逻辑函数的卡诺图化简法逻辑函数的卡诺图化简法1.6.3 逻辑函数的卡诺图化简法逻辑函数的卡诺图化简法3.卡诺图卡诺图变量卡诺图的特点：（1）用几何相邻形象地表示变量各个最小项在逻辑上的相邻性。 在卡诺图中，凡是几何相邻的最小项，在逻辑上都是相邻的。（2）卡诺图的主要缺点是，随着变量个数的增加，

38、图形迅速地复杂起来。当变量多于六个时，不仅画图十分麻烦，而且即使画出来了，许多的小方块最小项，是否逻辑相邻，也难以辨认，已无实用价值。1.6.3 逻辑函数的卡诺图化简法逻辑函数的卡诺图化简法3.卡诺图卡诺图几何相邻：包括三种情况。一是相接紧挨着；二是相对任一行或一列的两头；三是相重对折起来后位置重合。逻辑相邻：如果两个最小项，除了一个变量的形式不同外，其余的都相同，那么这两个最小项称为在逻辑上是相邻的。而在逻辑上相邻的最小项，是可以合并的。4.4.逻辑函数的卡诺图表示逻辑函数的卡诺图表示 （1 1）最小项表达式）最小项表达式卡诺图卡诺图 例例1.6.21.6.2 画出以下逻辑函数的卡诺图：画出

39、以下逻辑函数的卡诺图： )15,14,11,10, 8 , 4 , 3 , 2 , 1 , 0(),(mDCBAL解：解：1.6.3 逻辑函数的卡诺图化简法逻辑函数的卡诺图化简法4.4.逻辑函数的卡诺图表示逻辑函数的卡诺图表示解：解： （2 2）逻辑函数）逻辑函数卡诺图卡诺图 例例1.6.31.6.3 画出逻辑函数画出逻辑函数 的卡诺图。的卡诺图。 BCABL方法一：逻辑函数方法一：逻辑函数最小项表达式最小项表达式卡诺图卡诺图方法二：直接填方法二：直接填1.6.3 逻辑函数的卡诺图化简法逻辑函数的卡诺图化简法 1. 化简步骤化简步骤：（1）将逻辑函数化为最小项之和的形式；）将逻辑函数化为最小项

40、之和的形式；（2）填卡诺图；）填卡诺图；（3）按照合并规则（三个性质）画包围圈合并最）按照合并规则（三个性质）画包围圈合并最小项；小项；（4）写出最简与）写出最简与-或表达式。或表达式。 注：步骤（注：步骤（1）可以省略。）可以省略。1.6.3 逻辑函数的卡诺图化简法逻辑函数的卡诺图化简法 合并规则合并规则：（1）圈大好）圈大好能合并的最小项的个数越多越好；能合并的最小项的个数越多越好；（2）有新意）有新意每个圈中至少应含有一个没有被其每个圈中至少应含有一个没有被其他圈包含的新的最小项；他圈包含的新的最小项；（3）覆盖完）覆盖完圈完函数的全部最小项。圈完函数的全部最小项。1.6.3 逻辑函数的

41、卡诺图化简法逻辑函数的卡诺图化简法例例1.6.4 1.6.4 试用用卡诺图法化简逻辑函数：试用用卡诺图法化简逻辑函数：解：解：DBABCABDDABAF BCDBAF （1）卡诺图）卡诺图（2）画包围圈）画包围圈（3）最简与）最简与-或表达式或表达式1.6.3 逻辑函数的卡诺图化简法逻辑函数的卡诺图化简法例例1.6.5 1.6.5 试用用卡诺图法化简逻辑函数：试用用卡诺图法化简逻辑函数：解：解：（1）卡诺图）卡诺图（2）画包围圈）画包围圈（3）表达式）表达式BDDABCDCBADCBACDBAF ABCCDADCACBAF1.6.3 逻辑函数的卡诺图化简法逻辑函数的卡诺图化简法1.6.3 卡诺

42、图化简法卡诺图化简法例例1.6.6 1.6.6 试用用卡诺图法化简逻辑函数：试用用卡诺图法化简逻辑函数：解：解：)15,14,13,12,11,10, 9 , 8 , 7 , 6 , 2 , 0(),(mDCBAFDBBCADCBAF ),(1.6.4 具有无关项的逻辑函数化简具有无关项的逻辑函数化简 定义：定义： 受实际问题约束，某些输入变量的取受实际问题约束，某些输入变量的取值组合不允许出现，或出现后逻辑值任意。这样的值组合不允许出现，或出现后逻辑值任意。这样的取值组合所对应的最小项称为无关项。取值组合所对应的最小项称为无关项。 无关项也称任意项或约束项。无关项也称任意项或约束项。 根据逻

43、辑命题写出逻辑函数通常有两大类；一根据逻辑命题写出逻辑函数通常有两大类；一类逻辑函数的逻辑值是完全确定的，它不是逻类逻辑函数的逻辑值是完全确定的，它不是逻辑辑1就是逻辑就是逻辑0，这类逻辑函数的化简可按上述，这类逻辑函数的化简可按上述的方法进行；的方法进行；另一类逻辑函数值对于某些最小项却是不完全另一类逻辑函数值对于某些最小项却是不完全确定的，这类逻辑函数又有以下两种情况：确定的，这类逻辑函数又有以下两种情况：1.6.4 具有无关项的逻辑函数化简具有无关项的逻辑函数化简1）任意项任意项: 输入变量的某些取值的组合根本不存在，输入变量的某些取值的组合根本不存在，或者某些取值的组合也确实存在，但它的存在对逻或者某些取值的组合也确实存在，但它的存在对逻辑函数的输出没有任何影响。辑函数的输出没有任何影响。2）约束项约束项: 输入变量的某些取值的组合实际存在，但输入变量的某些取值的组合实际存在，但对逻辑函数来讲