第1讲三角形的倒角练习

1、精选优质文档-倾情为你奉上与三角形有关的角知识回顾一、什么是三角形内角？三角形相邻两边组成的角叫做它的内角二、什么是三角形的外角？三角形的外角与相邻的内角互为邻补角，因为每个内角均有两个邻补角，因此三角形共有六个外角，其中有三个与另外三个相等每个顶点处的两个外角是相等的知识讲解三角形内角和定理：三角形三个内角和等于三角形的外角：三角形的外角与相邻的内角互为邻补角，因为每个内角均有两个邻补角，因此三角形共有六个外角，其中有三个与另外三个相等每个顶点处的两个外角是相等的三角形的外角和：每个顶点处取一个外角，再相加，叫三角形的外角和(并非个外角之和)三角形的外角和等于三角形内角和定理的三个推论：推论

2、1： 直角三角形的两个锐角互余推论2： 三角形的一个外角等于和它不相邻的两个内角的和 推论3： 三角形的一个外角大于任何一个和它不相邻的内角三角形内角和的几种证明方法：添加平行线法： 帕斯卡(法国数学家)折纸法：更具动手可行性的剪角法：(不严密)把三角形的三个内角剪下来能拼成一个平角三角形外角和的证明法：三角形按最大角的大小来分类： 三角形的角与不等式：若为锐角三角形，则，；若为直角三角形，且，则，若为钝角三角形，且，则，多边形及其内角和 基本概念 多边形的定义：在平面内，由一些线段首尾顺次相接组成的图形叫做多边形 多边形的边：组成多边形的各条线段叫做多边形的边 多边形的顶点：每相邻两边的公共

3、端点叫做多边形的顶点 多边形的对角线：在多边形中，连接多边形不相邻的两个顶点的线段，叫做多边形的对角线 多边形的内角：多边形相邻两边组成的角叫做它的内角 多边形的外角：多边形的边与它的邻边的延长线组成的角叫做多边形的外角 正多边形：各个角相等，且各条边都相等的多边形叫做正多边形 凸多边形：如果多边形的任何一边所在直线都使余下的边都在这条直线的同一侧的多边形 基本性质 稳定性 内角和与外角和定理如下图，边形的内角和为，多边形的外角和都是 边形的对角线：一个顶点有条对角线，共有条对角线 不特别强调多边形都指凸多边形，凸多边形的每个内角都小于同步练习板块一、三角形内角和【例1】 已知在中，则的度数是

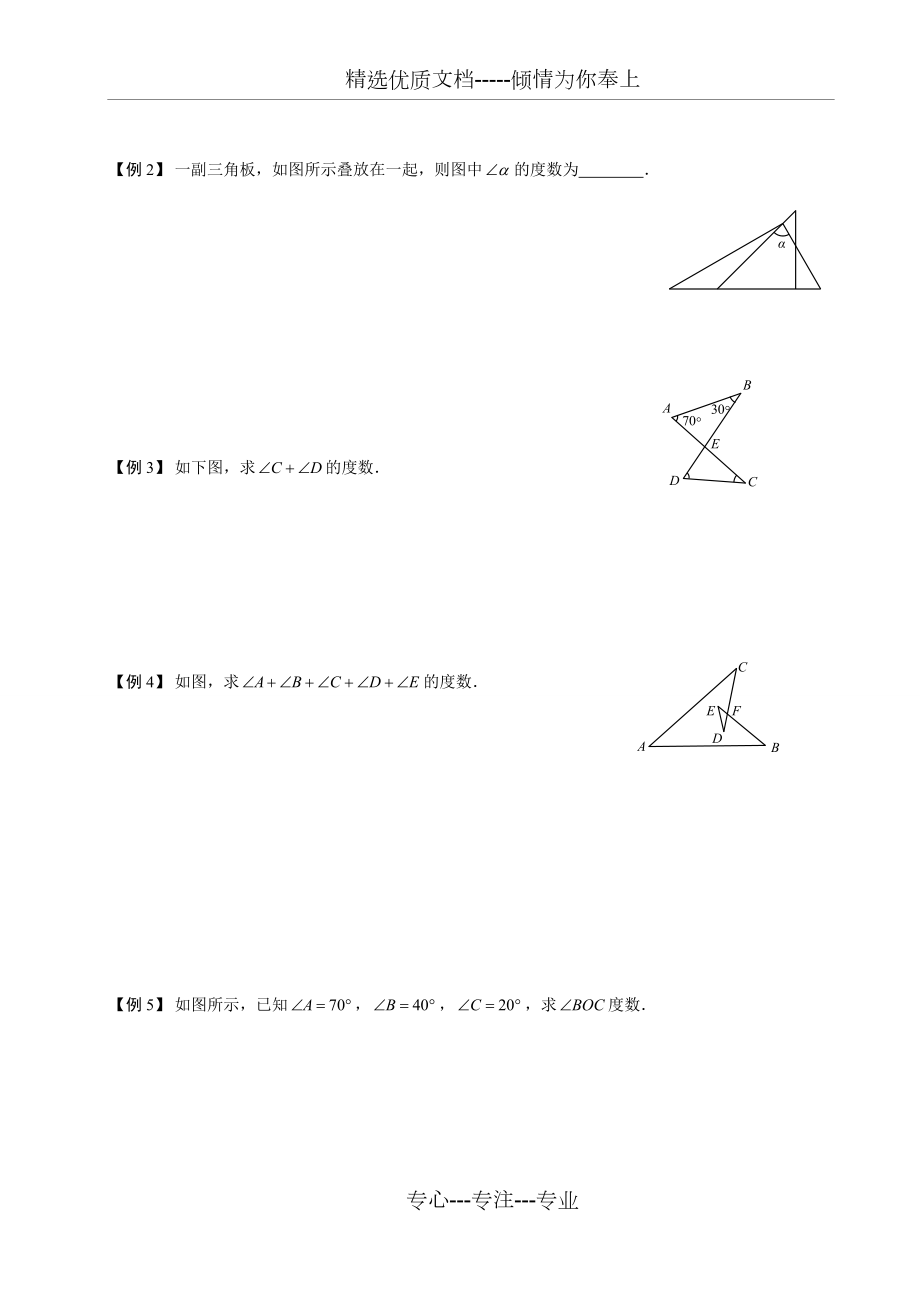
4、( )A B C D【例2】 一副三角板，如图所示叠放在一起，则图中的度数为 【例3】 如下图，求的度数【例4】 如图，求的度数【例5】 如图所示，已知，求度数【例6】 如图所示，已知，试探索的度数【例7】 如下图，已知，求 【例8】 如下图，中，剪去后，得到四边形，则 【例9】 如图所示，将沿着翻折，若，则 【例10】 如图，求的值【例11】 如图在三角形纸片中，将纸片的一角折叠，使点落在内，若，则为多少度？【例12】 若三角形的三个外角的比是，则这个三角形的最大内角的度数是 【例13】 如下图所示，在中，、为上两点，若，求证：【例14】 已知三角形有一个内角是度，最大角与最小角之差是求的取

5、值范围【例15】 如图，求的大小板块三、涉及角平分线的图形中角的关系【例16】 如右图所示，是的角平分线，是的角平分线，、交于，试探索与之间的关系： 【例17】 如右图所示，是的外角平分线，也是的外角平分线，、交于点，试探索与之间的关系： 【例18】 如图，在三角形中，和的三等分线分别交于、，求的度数【例19】 如图，延长四边形对边，交于，交于若，的平分线交于，求证：【例20】 如图，是的角平分线，是角的平分线，与交于，若，求的度数课后练习【习题1】 如图，求 【习题2】 如下图，求的度数【习题3】 如下图，求 【习题4】 已知的三个内角为，令， ，则，中锐角的个数至多为( )A个 B个 C个 D