一种台灯罩注塑模具设计【1模2腔含11张CAD图】
收藏
资源目录

压缩包内文档预览:(预览前20页/共39页)
编号:10265901
类型:共享资源
大小:13.17MB
格式:ZIP
上传时间:2018-07-05
上传人:QQ14****9609
认证信息
个人认证
郭**(实名认证)
陕西
IP属地:陕西
50
积分
- 关 键 词:
-
一种
灯罩
注塑
模具设计
11
十一
cad
- 资源描述:
-
一种台灯罩注塑模具设计【1模2腔含11张CAD图】
【需要咨询购买全套设计请加QQ1459919609】图纸预览详情如下:
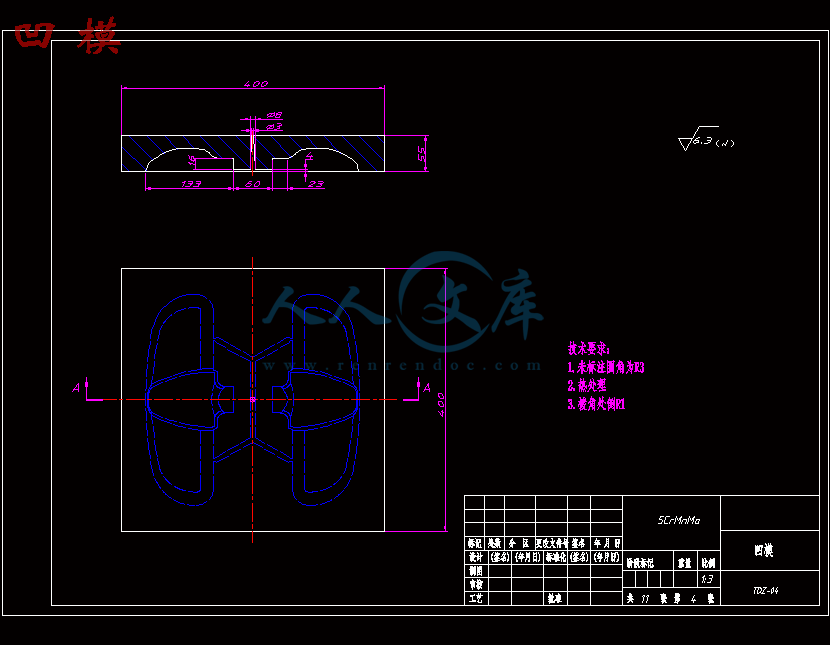
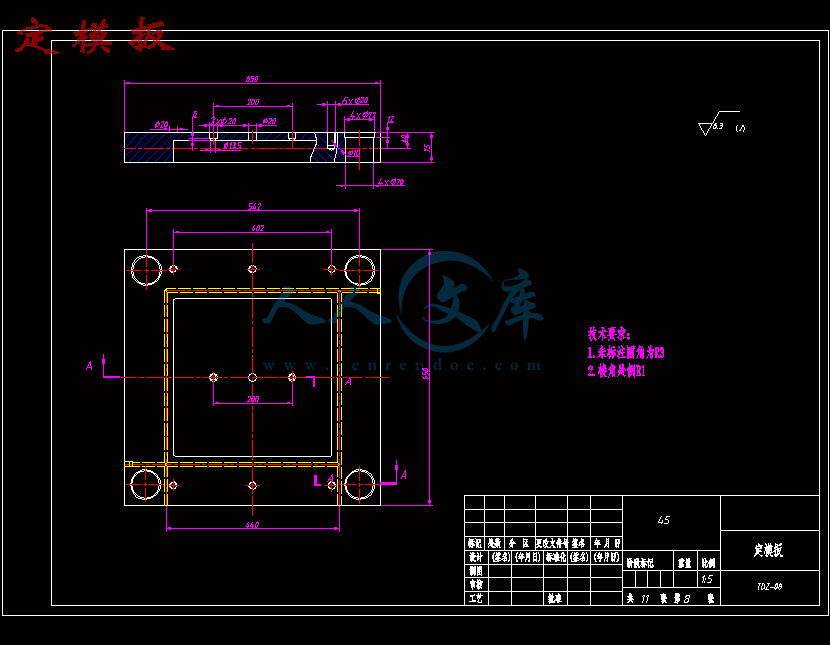











- 内容简介:
-
附 录 BInverse thermal mold design for injection moldsAddressing the local cooling demand as quality function for an inverse heat transfer problemCh. Hopmann1 P. Nikoleizig1Received: 26 September 2016 /Accepted: 7 December 2016 Springer-Verlag France 2016Abstract: The thermal mold design and the identification of a proper cooling channel design for injection molds becomes more and more complex. To find a suitable cooling channel system with objective rules based on the local cooling demand of the part a new methodology for the thermal mold design based on an inverse heat transfer problem was introduced. Based on a quality function regarding production efficiency as well as part quality, additional aspects to model the injection molding process are dis- cussed. Aim of those extensions is the improvement of the inverse optimization of the problem.Keywords: Injection molding, Thermal mold design, Inverse heat transfer problem, Heat transferIntroductionWith injection molding, increasingly complex components can be produced, but at the same time the requirements of the necessary injection mold rise. Concurrently due to the economic pressure, e.g. by global competition, strives for high efficiency and short production cycles are essential. Since the injection molding cycle is primarily characterized through the cooling of the melt into a dimensionally stable state, it is contiguous to focus on the cooling channel system of the injection mold for additional improvement in efficiency (Fig.1b). Usually, the cooling channels are realized through bores in the injection mold, which are connected by fittings to a complete channel system. Innovative technologies such as the selective laser melting (SLM) now enable the layered structured buildup of molds from metal pow- der. With this approach, the cooling channel system can be generated almost in any desired shape and course. The creation of a proper cooling channel system is a challenging task, also hindered by these opportunities and at the same time more complex parts.28Additionally thermal mold design phase is impeded due to particular thermoplastic materials, which are often used in technical parts and tend to a comparatively large shrinkage (Dependent on temperature and pressure) as a result of the crystallization process (as illustrated in Fig. 1a between points 3 to 5). This shrink- age causes stresses inside the part, if local differences in the shrinkage potential occur. Furthermore, the stresses can only be compensated through a deformation of the part. This so-called warpage may prevent the correct usage of the part and therefore must be avoided 1, 2.State of the artBesides the wish for a fast and efficient injection molding cycle, the aforementioned challenges lead to investigations to describe and simplify the thermal mold design phase. The efforts reach from a transfer of analytical approaches into the computer aided design to full mathematical and computational descriptions of the solidification process. Those efforts have a forward looking character and need an intense interpretation after the solution is calculated. A fully auto- mated thermal mold design phase is still not available.Fig.1Visualisation of the injection molding cycle with process variables (a) and a pie chart (b)Nowadays, this issue is progressively addressed through different research activities into a user independent optimization strategy for a proper cooling channel design (e. g. 35).Mehnen et al. rely on the use of evolutionary algorithms and model a mold29system based on light exchanging surfaces 3. The heat exchange is then calculated by a ray tracing method, which is faster than solving all governing equations. Spheres are used only in the first step of the sys- tem as parts to be analyzed. Maag and Kufer, in contrast, study a cluster algorithm which is combined with a branch and bound search algorithm to find the ideal cooling channel position 4. Contrarily, Fanacht et al. approach an auto- mated tempering system positioning by an artificial neural network, which covers numerous problems concerning temperature control 5. This also means that solutions may only come from the space of simulated training problems respectively from the possible interpolations in between. Common to all of these approaches is the forward headed nature which emphasizes the cooling channel system, but the evaluation is only possible after the simulation 35.Though also for those computer-aided optimizations a precise definition of the tempering system design is necessary in advance and essential for the quality of the result. Without knowledge regarding the local cooling demand for minimal part warpage and control of the polymer a targeted use of an optimization is not possible. Hassan et al. focus mainly on the criteria of part quality and study possibilities to realize a dynamic cavity tempering as well as a description of the influence of the cooling channel system on shrinkage and cooling of plastics 6. Thereby, an auto- mated generation of cooling channel systems is not the main focus of their work. Finally Agazzi et al. show a promising approach which is based on an inverse heat conduction problem 7, 8. Thus, in this case a part is defined as polymerwith homogeneous temperature. Along a given cooling area, surrounding the part, an optimized temperature distribution is calculated with a conjugate gradient algorithm in respect to a given objective function, which is based on fast heat removal as well as a homogeneous part temperature. Indeed, an inverse design is performed, but also along the analytical approach of thermal homogeneity.Setup of the proposed methodologyIn the light of the aforementioned technical development, the work of Agazzi et al. seems to be a promising starting point for further investigation.Besides a significant improvement for part warpage, their approach also shows some simplifications. For example the phases of the injection molding cycle are not modelled and implemented in the optimization. This refers especially to the injection and the holding pressure phase. Also the objective function refers to a rapid cooling and a homogeneous part temperature as the two aims 8. This approach seems30reasonable, but regarding to the phases of the injection molding cycle and the temperature and pressure dependent pvT-behavior, a different design of the objective function can be considered. Also the derived cooling channels require further investigations.Within the framework of the here proposed expanded methodology a model is favored, which also considers the following aspects. First the methodology should be able to include more phases of the injection molding process. So it is based on a conventional injection molding simulation. Results for pressure, temperature and inner properties can be exported at different stages of the process as boundary conditions for the optimization. So the expanded methodology is based on a hybrid simulation approach, which connects injection molding simulation with optimizing an inverse heat transfer problem. Also the objective function should be redesigned carefully. On one hand, the design should address minimal cycle times to fulfil the request for an efficient process like the one used by Agazzi et al.On the other hand, also part quality should be addressed, which refers to mechanical, visual and geometric requirements. Whereas mechanical and visual properties can be met by appropriate slow cooling rates, especially geometric proper- ties, paraphrased the dimensional accuracy of the part, turn out to be a severe element of the thermal mold design phase. By using a proper tempering system, a locally homogeneous shrinkage should be targeted to minimize the tendency of the part to warp. The objective of the analysis is to bring local heat and cooling demand of the part in equilibrium to local heat and cooling supply of the molds tempering system.The postulate of an even shrinkage potential can be modelled via homogeneous local densities as an objective function, so that the problem is still addressable as an inverse heat conduction problem 9.A modified exemplary extended objective function to be introduced to the31methodology is given in Eq. 1.This objective function Q(TC ) addresses a quick cooling through the first term, where a desired ejection temperatureTEjec for the surface 1 of the part is given and compared to the actual local temperatures Tloc (xi,t,TC) of the part. The second term addresses density homogeneity, with the differences of local density loc (xi,t,TC) compared to a mean density Ejec, which should be reached on a surface 2 within the part. Both terms are integrated over their respective areas 1/2 and can be weighted with the variable wm/k. The temperatures Tc on the outer mold contour according to Fig. 2b are then varied to minimize the quality function.For the proposed approach the exact modeling of the designed methodology will be carried out as a hybrid simulation approach, containing an injection molding simulation as input for a heat conduction simulation calculated with a multiphysics simulation. With this hybrid approach, all plastics related properties and more phases of the injection molding cycle can be modelled and made available for a thermal optimization at the same time.With the presented objective function an exemplary cooling channel system for a plate shaped specimen with ribs is analyzed 10,13,14. Measurements of the specimen are shown on Fig. 2a. Simultaneously, the specimen contains typical elements of injection molded parts with three ribs in different heights. The thickness of the specimen is 1.5 mm, which is typical for injection molded parts. Based on the specimens geometry a cooling area is generated, with a constant distance to the part and an area inside the part, for which the objective function is solved (see Fig. 2b). The specimen is optimized using a 2D calculation approach, in order to save computing time.After solving the optimization for density and cooling time, as stated in Eq.1 also with a conjugate gradient algorithm, the cooling channels can be derived from isothermal lines of the desired mold temperature of 80C 10. The gradient algorithm follows the steepest ascent of the objective function and calculates the necessary temperature distribution along the outer mold contour defined as cooling area to minimize the objective function. The input datafields for the optimization are shown in Fig.3a. Based on the result of the optimization, which is shown in Fig. 3b, the cooling channels were identified. Although, temperature distribution of the optimization lead to very low temperatures of 100 C, this distribution can be used to32derive the contour of a cooling channel by using an isothermal line. Those derived 2D channel contours are then modelled as extruded 3D geometries. With the injection molding simulation software Sigmasoft, Sigma engineering GmbH, Aachen, Germany, an entire 3D injection molding simulation is set up using the boundary conditions presented in Table 1. The implemented material is a widely used polyamide 6 (unfilled B 30 S) of Lanxess AG, Cologne, Germany (see Table 2 for properties). In Fig.4 two different setups of the specimen are presented and compared. One is modelled without cooling channels as a neutral reference and a second one with the derived cooling channels from the optimization. Figure 4a illustrates the resulting temperature distribution inside the mold. Figure 4b shows the resulting warpage of the specimen. Comparing these two cases, a significant reduction of the specimens warpage can be achieved, with the second case resulting in a relatively low warpage of the specimen. Merely, the end of the ribs show bigger deviations from the original geometry in both cases. Here, it has to be noted, that in the scope of the optimization, heat has to be brought into the system as shown in Fig. 3b. This demand is not yet considered, as the standard process uses just cooling. In addition the natural thermal shrinkage of the part has to be taken into account, which is already included in the results, due to the simulation software. This natural shrinkage is not part of the optimization yet.Fig. 2 Specimen with ribs and measurements (a) and outer contour around part(b)Fig. 3 Mold contours, initial temperatures (a), optimization,results and derived33cooling channel system (b)a) Initial data of temperature and pressure distributionb)Temperature distribution at optimization pointFurther extension of methodologyWith the principle functionality of the methodology shown, it will be investigated to what extent a more accurate.Table 1 Settings for the optimization calculation and the injection molding simulation of cooling and shrinkage and warpage.ParameterMelt temperature 270 CEjection temperature 110 CCooling fluid temperature 80 CInjection pressure 1000 barHolding pressure 800 barCycle time 5.6 sHandling time 1.5 sInjection time 0.248 sHolding pressure time 3.1 sTable 2 Material properties of the implemented mold and plastic 11, 1234ParameterDensity steel 7830 kg/m3 Heat conductivity steel 46.5 W/m K Heat capacity steel 440 J/kg KDensity modeling PA 6 Tait-approachacc. to material supplierViscosity modeling PA 6Cross-WLF-approach acc. to material supplierHeat conductivity PA 60.2 W/m KHeat capacity PA 6 2390 J/kg KHeat transfer coefficients 2000W/m2Fig.4 Resulting temperatures (a) and warpage (b) of the specimen for a 3D simulation without (upper part) and with automatically derived cooling channels for minimal part warpage (lower part)a) Temperature distribution at the end of the cooling phase after 15 cycles Without cooling channels:With derived cooling channels:b) Deformation of the part: Visual amplification factor: 2035Modeling of the injection molding process can increase the quality of the results, in comparison to the work of Agazzi et al.This will be presented with the following three additional aspects. The implementation of a multi- cycle approach should be discussed first. The influence of a modeling of the handling times will follow. And finally the modeling of the injection phase will be investigated. Unless specifically stated, besides heat conductivity of the mold, which is changed to more suitable mold making steel of 25.3 W/m K, all other material properties and boundary conditions remain the same 14.Implementation of multicycle analysisUsually the injection molding process is used to produce a large quantity of molded parts with the same geometry.This is done through the periodic repetition of the molding. Assuming a uniform temperature distribution in the mold at the beginning of the first cycle, a temperature distribution adjusts itself after some cycles 1. Local cooling demand for warpage minimized cooling of the part should be deter- mined in the stable state, because it is otherwise
- 温馨提示:
1: 本站所有资源如无特殊说明,都需要本地电脑安装OFFICE2007和PDF阅读器。图纸软件为CAD,CAXA,PROE,UG,SolidWorks等.压缩文件请下载最新的WinRAR软件解压。
2: 本站的文档不包含任何第三方提供的附件图纸等,如果需要附件,请联系上传者。文件的所有权益归上传用户所有。
3.本站RAR压缩包中若带图纸,网页内容里面会有图纸预览,若没有图纸预览就没有图纸。
4. 未经权益所有人同意不得将文件中的内容挪作商业或盈利用途。
5. 人人文库网仅提供信息存储空间,仅对用户上传内容的表现方式做保护处理,对用户上传分享的文档内容本身不做任何修改或编辑,并不能对任何下载内容负责。
6. 下载文件中如有侵权或不适当内容,请与我们联系,我们立即纠正。
7. 本站不保证下载资源的准确性、安全性和完整性, 同时也不承担用户因使用这些下载资源对自己和他人造成任何形式的伤害或损失。

人人文库网所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
 川公网安备: 51019002004831号
川公网安备: 51019002004831号